Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería y Ciencia
Print version ISSN 1794-9165
ing.cienc. vol.11 no.21 Medellín Jan./June 2015
https://doi.org/10.17230/ingciencia.11.21.3
ARTÍCULO ORIGINAL
doi:10.17230/ingciencia.11.21.3
Optimización de manipulabilidad y consumo eléctrico mediante el Algoritmo Heurístico de Kalman en manipuladores seriales
Optimization of Manipulability and Electricity Consumption Through the Heuristic Kalman Algorithm in Serial Manipulators
Juan Camilo Ramírez Henao1 y Leonardo Duque Muñoz2
1 Instituto Tecnológico Metropolitano, Medellín, Colombia, juanramirez101271@correo.itm.edu.co.
2 Instituto Tecnológico Metropolitano, Medellín, Colombia, leonardoduque@itm.edu.co.
Recepción: 27-11-2013 | Aceptación: 20-05-2014 | En línea: 30-01-2015
MCS: 80M50
Resumen
En el presente trabajo se plantea una metodología de planeación de trayectorias para manipuladores seriales antropomórficos de seis grados de libertad y muñeca esférica enfocada en la minimización del consumo eléctrico y maximización de la manipulabilidad. Para lograr tal fin se expone un algoritmo de optimización el cual tiene como base el Algoritmo Heurístico de Kalman (AHK), cuya finalidad es encontrar la trayectoria óptima según la función multi-objetivo propuesta dentro de un espacio esférico simplificado propuesto. El algoritmo de optimización se evalúa mediante el análisis del comportamiento de dos trayectorias en el manipulador PUMA 560, simuladas en un programa desarrollado en la aplicación de Visual Basic perteneciente al software Autodesk Inventor. planeación de trayectorias; robótica; optimización
Palabras clave: multi-criterio; algoritmo heurístico; manipulabilidad; consumo eléctrico
Abstract
In the present work a path planning methodology for serial anthropomorphic manipulator with six degrees of freedom with spherical wrist focused on minimizing power consumption and maximizing the manipulability is proposed. To achieve this end, an optimization algorithm is developed which is based on the Heuristic Kalman Algorithm (HKA), and aims to find the optimal path according to the proposed multi-objective function within a proposed simplified spherical space. The optimization algorithm is evaluated by analyzing the behavior of two paths in the PUMA 560 robot, simulated in a program developed in Visual Basic belongs to Autodesk Inventor software.
Key words: path planning; robotics; multi-criteria optimization; heuristic algorithm; manipulability; electric consumption
1 Introducción
Los robots manipuladores son herramientas idóneas para automatizar muchos de los procesos productivos, gracias a que estos aumentan la productividad y calidad, y disminuyen los costos de producción y mano de obra [1]. Sin embargo, para garantizar un aumento en la productividad el rendimiento de los manipuladores debe ser maximizado. Esto puede ser realizado mediante una adecuada planeación de la trayectoria del robot, utilizando técnicas de optimización de alguna función objetivo o de sus parámetros[2].
La eficiencia con la cual los desplazamientos articulares de un robot se convierten en movimientos de su órgano terminal, llamado índice de manipulabilidad, es un criterio usado para cuantificar este desempeño. Uno de los métodos más comunes encontrados en la literatura para medir la manipulabilidad es el propuesto por Yoshikawa [3] y ha sido usado como base en trabajos que desarrollan métodos para planeación de trayectorias en manipuladores robóticos [4],[5],[6].
Planear la trayectoria del manipulador usando el criterio de minimización del consumo eléctrico como función genera trayectorias suaves, que son fáciles de rastrear y reducen los esfuerzos en los actuadores y la estructura del manipulador. Adicionalmente este criterio permite considerar la pérdida de energía resistiva en el bobinado del motor, al igual que la perdida de energía debido a las variaciones en las velocidades del actuador. Estas variaciones afectan los requerimientos de corriente y por lo tanto inducen fuerzas electromotrices en los actuadores [7].
Entre las investigaciones que usan este criterio como función objetivo para la planeación de trayectorias se encuentra el enfoque propuesto por [8] en el cual desarrollan un algoritmo genético para robots planos de tres grados de libertad buscando la minimización de la energía consumida por cada motor del brazo robótico durante la trayectoria. Esta investigación se basa en un método de en un solo criterio.
A diferencia de la optimización individual, donde se trata de encontrar la mejor solución, la misión de la optimización multi-criterio es encontrar la solución con los menores objetivos en conflicto [9].
En las investigaciones recientes que aplican una metodología multi-criterio para planeación de trayectorias considerando los parámetros de manipulabilidad y consumo eléctrico simultáneamente, destacan la realizada por [10] en la cual usan una técnica Lagrangiana Aumentada aplicada en máquinas cinemáticas paralelas, y el enfoque propuesto por [11] en el cual desarrollan dos técnicas de optimización evolutiva llamadas: Algoritmo Genético de Ordenación No-Dominada Elitista (Elitist non-dominated sorting genetic algorithm - NSGA-II) y Evolución Diferencial (Differential Evolution: DE) aplicadas en manipuladores tipo SCARA de cuatro grados de libertad.
Basándose en el planteamiento anterior y tomando en consideración que la mayoría de los manipuladores usados en tareas industriales son seriales por ser más comunes y asequibles comercialmente [12], se evidencia una oportunidad de investigación en enfoques de planeación de trayectoria multi-objetivo para manipuladores seriales antropomórficos de seis grados de libertad y muñeca esférica desarrollados mediante métodos heurísticos tales como el Algoritmo Heurístico de Kalman (Heuristic Kalman Algortihm − HKA), el cual fue propuesto por [13].
En el presente artículo se expone un método de optimización multi −objetivo implementado en el manipulador PUMA 560, que integra la minimización del consumo de energía eléctrica y aumento de manipulabilidad basado en el Algoritmo Heurístico de Kalman, idóneo para procedimientos de búsqueda basados únicamente en los valores de la función objetivo, sin necesidad de suposiciones fuertes tales como linealidad, diferenciabilidad, convexidad entre otros.
2 Desarrollo del método de optimización
2.1 Esquema inicial manipuladores antropomórficos de seis grados de libertad con muñeca esférica
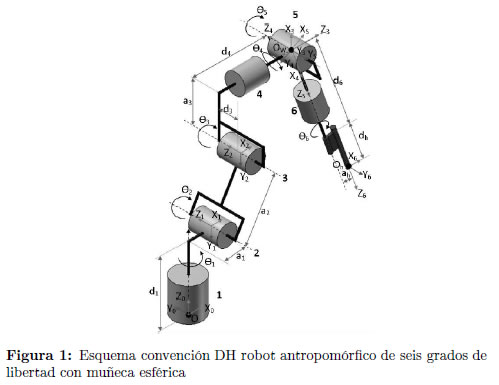
Partiendo del esquema del manipulador antropomórfico de seis grados de libertad con muñeca esférica representado en la Figura 1 se procede a identificar las variables base del modelo cinemático (Tabla 1) basado en la convención Denavit Hartenberg (DH) el cual es el punto de partida del método de optimización planteado en el artículo.2.2 Espacio de trabajo simplificado en manipuladores antropomórficos de seis grados de libertad con muñeca esférica
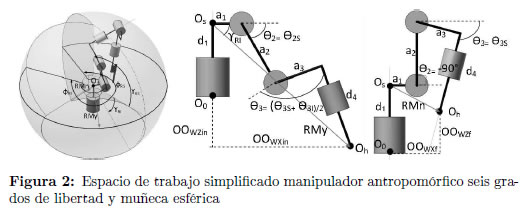
El espacio de trabajo del manipulador antropomórfico de seis grados de libertad y muñeca esférica será tomado como un espacio esférico, ubicando su origen en el punto final de la distancia d1 (Os) propia del manipulador, y estará delimitado por un radio mayor (RMy) y menor (RMn) el cual comprende la distancia hasta la muñeca del manipulador (Oh), un ángulo de colatitud superior (γRS) e inferior (γRI) y un ángulo azimutal superior (ϕRS) e inferior (ϕRI) Figura 2.
Partiendo de los siguientes datos para las articulaciones del manipulador:
θ1=0°, θ2=θ2S, donde θ2S es límite superior de la articulación 2 del manipulador. θ3 = (θ3S+θ3I), donde θ3S es límite superior de la articulación 3 del manipulador y θ3I es límite inferior de la articulación 3 del manipulador. θ4=180°, θ5=0° y θ6 = 0°
Además, con base al esquema del manipulador de la Figura 2, y hallando las coordenadas (OOwxin, OOwyin, OOwzin) del origen de la muñeca (Oh) del manipulador, se calcula la Ecuación del radio mayor del espacio de trabajo(RMy):
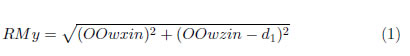
El radio menor (RMn) se calcula de igual forma, pero se toman los siguientes datos para las articulaciones del manipulador:
θ1=0°, θ2=−90°, debido a que es el ángulo en el cual la articulación 3 se encontrará más alejada verticalmente de la base. θ3=θ3S, donde θ3S es límite superior de la articulación 3 del manipulador. θ4=180°, θ5=0° y θ6=0° Por consiguiente la Ecuación (2) del radio menor es:
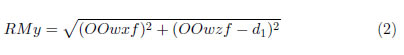
La Ecuación (3) del ángulo inferior de colatitud (γRI) es:
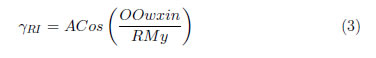
Y se fija el valor del ángulo superior de colatitud (γRS) en −90°, abarcando con esto el cuadrante superior de la esfera del espacio de trabajo.
Los ángulos azimutal límites del espacio de trabajo corresponden con los ángulos límites inferior y superior de la articulación 1, por consiguiente:

Por último las Ecuaciones (5) de las coordenadas cartesianas de un punto dentro del espacio de trabajo simplificado según las variables halladas son:
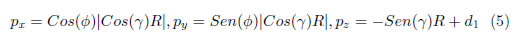
2.3 Manipulabilidad de manipuladores seriales
El método para realizar el cálculo de la manipulabilidad se basa en el descrito en [14] el cual propone descomponer un manipulador de seis grados de libertad con muñeca esférica en dos secciones, una compuesta por las tres primeras articulaciones de rotación, la cual será llamada sección de brazo, y la otra por las tres articulaciones restantes que conforman la sección de la muñeca esférica, con el fin de hallar la manipulabilidad translacional y rotacional del manipulador al igual que sus singularidades [15]. Aplicando este método al manipulador antropomórfico de seis grados de libertad y muñeca esférica, se tiene que la Ecuación (6) de la manipulabilidad total es igual a:

Donde la Ecuación (7) de la manipulabilidad translacional o de brazo es igual a:
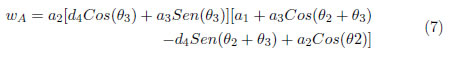
Y la Ecuación (8) de la manipulabilidad rotacional o de muñeca es igual

2.4 Consumo de energía en manipuladores seriales
Los motores de Corriente Directa (CD) y de imán permanentes, hoy en día son los de uso más común en el campo de la robótica [16]). En estos la corriente eléctrica varía con las velocidades y torques sobre ellos. Por consiguiente, en este tipo de motores, aparece el fenómeno de auto-inductancia. La corriente I y el potencial electromotriz Ve de los motores pueden calcularse como una función del torque requerido τm y la velocidad angular ω de los actuadores, es decir,

Donde Kt es el factor de sensibilidad del motor o constante de motor expresada en (Nm/A) y Ke la constante de fuerza contra electromotriz expresada en (V*(rad/seg)−1).
La Ecuación (13) de la potencia eléctrica total PT se compone de:
Pérdida de potencia resistiva (Efecto Joule):

Potencia usada para producir la fuerza electromotriz:

Por consiguiente, la potencia eléctrica total PT, puede expresarse como:

Donde R es la resistencia de la armadura del motor expresada en Ohm.
Finalmente, Ecuación (14) de la energía E consumida por el motor puede ser evaluada mediante la integración de PT sobre el tiempo total T de la trayectoria:

Debe tenerse en cuenta que la Ecuación (9) de la corriente I, permite considerar la energía utilizada por los actuadores cuando estos no se mueven, pero producen un torque que mantiene el manipulador en una cierta configuración estacionaria (respecto a una dirección particular del actuador), suficiente para resistir la gravedad [7].
2.5 Algoritmo Heurístico de Kalman
El Algoritmo Heurístico de Kalman es propuesto por Toscano y Lyonnet [17]. Este método utiliza una Función de Densidad de Probabilidad Gaussiana (FDPG), como proceso de medición, y un estimador de Kalman que permite mejorar la calidad de la estimación obtenida a través del proceso de medición. La FDPG evoluciona en el espacio de búsqueda, tratando de encontrar la solución óptima del problema de optimización. Una FDPG se caracteriza por su vector de medias m, y su matriz de varianzas Σ. Para la búsqueda de la solución óptima, los parámetros de la FDPG son actualizados, teniendo en cuenta los puntos de muestra obtenidos a través de un proceso de medición, esto se hace usando un estimador de Kalman. El principio del algoritmo consiste en modificar el vector de medias y la matriz de varianzas del generador aleatorio hasta que una solución aceptable sea obtenida.
Los pasos del algoritmo para realizar la minimización de la función objetivo se describen a continuación.
Definir la cantidad de N vectores a producir en cada iteración, el número de mejores candidatos Nξ y el coeficiente de ralentización α, inicializando el vector de medias y la matriz de varianzas.
Generar una secuencia de N vectores q1(k), q2(k), ... qN(k) para cada iteración k, de acuerdo a la distribución Gaussiana parametrizada por el vector de medias y la matriz de varianzas.
Realizar el proceso de medición, el cual consiste en calcular el promedio de los candidatos más representativos del óptimo en cada iteración k.
Actualizar la regla del generador Gaussiano.
Chequear la regla de paro. Si la regla de paro no se satisface ir al paso del generador Gaussiano, de otra manera se detiene en el paso del generador Gaussiano.
2.6 Método optimización del Algoritmo Heurístico de Kalman aplicado a los criterios de consumo eléctrico y manipulabilidad del manipulador antropomórfico de seis grados de libertad y muñeca esférica
El algoritmo de optimización propuesto tiene como finalidad minimizar el criterio de consumo eléctrico de la trayectoria y maximizar la manipulabilidad promedio de la trayectoria (o minimizar 1−w), partiendo de la variación de la ubicación de la trayectoria por medio de las variables radio del espacio de trabajo (R), ángulo de colatitud (γ), y ángulo azimutal (ϕ), dentro de los límites del espacio de trabajo simplificado. La función objetivo o de costo a minimizar J(q), está compuesta por dos criterios: la minimización del consumo eléctrico de la trayectoria del manipulador y la maximización de la manipulabilidad de la trayectoria (o minimización de 1−w). La Ecuación (15) de la función de costo propuesta como base del algoritmo se presenta a continuación:
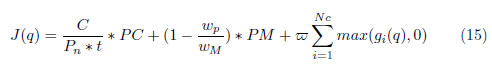
Dónde:
C: Consumo de la trayectoria en KWH
Pn: Potencia nominal del manipulador en Kw.
t: Tiempo de la trayectoria en horas.
PC: Peso asignado a criterio consumo eléctrico de la trayectoria (de 0 a 1).
wp: manipulabilidad promedio de la trayectoria.
wM: manipulabilidad máxima en el manipulador.
PM = 1−PC: Peso asignado a criterio de la manipulabilidad de la trayectoria (de 0 a 1).
ϖ: factor de peso para las restricción.
gi(q): Función de la restricción -esima.
Nc: Número de restricciones. Para este sistema se definieron 13 restricciones, siendo las restricciones 1 a 6 relacionadas con los límites articulares, las restricciones 7 a 12 con las velocidades articulares, y la restricción 13 relacionada con la potencia nominal del manipulador.
La inicialización del vector de medias y la matriz de varianzas del generador aleatorio es propuesta inicialmente según la Ecuación (16)

Sin embargo fue necesario replantear esta inicialización original del AHK porque debido a la cinemática inversa del brazo robot el algoritmo puede llegar a converger en una solución local. Para evitar esto se hace un sondeo rápido del espacio de trabajo con un delta constante para cada variable de decisión. De este sondeo se seleccionan los mejores candidatos y con estos se definen los nuevos límites del espacio de trabajo y las nuevas matrices de covarianza y varianza a usar como inicializadores del algoritmo. En la sección de resultados se hace una comparación de los dos casos (Figura 8).
La regla de paro del algoritmo se configura de forma tal que en 10 iteraciones seguidas el valor absoluto de la diferencia entre la iteración actual y la iteración anterior para 1−w sea menor a 0.0005, su consumo eléctrico menor a 0.0000001, y la función de costo sea menor a 0.9. Estos valores fueron hallados experimentalmente de acuerdo al método planteado por [17].
3 Caso de estudio: aplicación en el manipulador PUMA 560
3.1 Descripción manipulador PUMA 560
El manipulador PUMA (Programmable Universal Machine for Assembly) es un robot fabricado por Unimation en 1978 basado en diseños de un estudio realizado para General Motors [16]. Son manipuladores de seis grados de libertad con todas sus articulaciones rotacionales. También se caracterizan por tener su muñeca esférica debido a que los ejes de sus tres últimas articulaciones se intersecan en un punto común.El PUMA 560 cuenta en su eje final (articulación 6) con un acople que permite adaptar la herramienta necesaria para la tarea a realizar. Para esta investigación se escoge como herramienta final la pistola de soldadura de arco Tough Gun G2 del fabricante TreggasKiss la cual cuenta con el acople correspondiente y peso ideal para adaptarla al manipulador PUMA 560 (Figura 3).
Los límites de las velocidades articulares y los parámetros dinámicos del manipulador PUMA 560 fueron extraídos de diversas investigaciones que se especializaron en la identificación de cada uno de estos parámetros [18], [19]. Los parámetros de la pistola TOUGH GUN G2 se obtienen del catálogo del fabricante [20].
3.2 Descripción de trayectorias usadas para validación del método
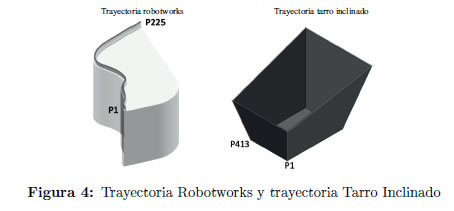
A continuación se describen dos trayectorias usadas para evaluar el comportamiento del método de optimización. La trayectoria Robotworks (Figura 4) consta de 225 puntos ubicados en el espacio cartesiano y fue obtenida a partir de dos archivos PanCirc.SRC y PanCirc.DAT disponibles en [21].La trayectoria Tarro Inclinado, consta de 413 puntos y fue obtenida a partir del espacio cartesiano mediante un algoritmo de extracción de líneas 3D identificadas en un sólido modelado en Autodesk Inventor 2013' (Figura 4).
3.3 Resultados
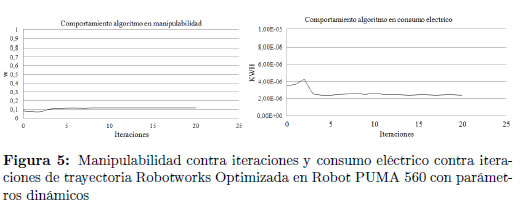
En esta sección se presentan los resultados del comportamiento del algoritmo de optimización con los parámetros de calibración seleccionados, aplicado en la trayectoria Robotworks y Tarro Inclinado realizadas en el robot PUMA 560.En la Figura 5 se aprecia el comportamiento de la manipulabilidad y del consumo eléctrico a medida que el algoritmo optimiza la trayectoria Robotworks en cada iteración. En ambos parámetros se cumple con el criterio de paro en la iteración 20.
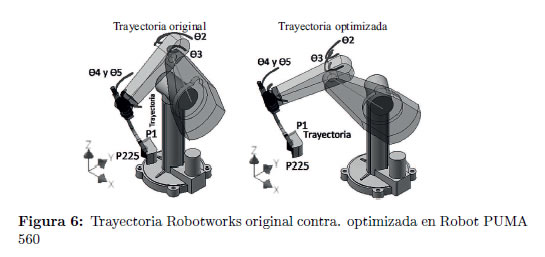
En la Figura 6 se identifican los recorridos que deben hacer las articulaciones del robot PUMA 560 para seguir la trayectoria Robotworks original y optimizada. Los datos del espacio de trabajo simplificado encontrados por el algoritmo al alcanzar el criterio de paro en la iteración 20 son: Radio = 0.61642617 m, Angulo R: 0.51938117 rad y Angulo P: −2.34115865 rad. Estos datos son el punto inicial dentro del espacio de trabajo de la nueva trayectoria optimizada.
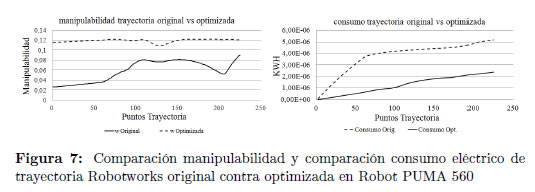
De la Figura 7 se aprecia que la manipulabilidad obtenida con la trayectoria optimizada es mayor y tiende a ser constante a lo largo del recorrido, comparándola con la original, situación que es favorable porque indica un aumento en el desempeño del manipulador en la ejecución de la trayectoria. Adicionalmente se aprecia que el consumo eléctrico a lo largo del recorrido de la trayectoria optimizada siempre es menor que el de la trayectoria original, al igual que el consumo final total.
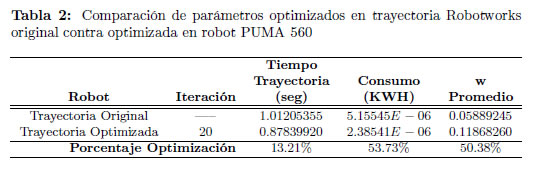
En la Tabla 2 se muestran los valores de los criterios de consumo eléctrico y la manipulabilidad promedio de la trayectoria Robotworks original y optimizada del robot PUMA 560, evidenciándose que el algoritmo de optimización en la iteración 20 logra optimizaciones del 53.73% en el consumo eléctrico, el 50.38% en la manipulabilidad, incluso del 13.21% en el tiempo de la trayectoria.
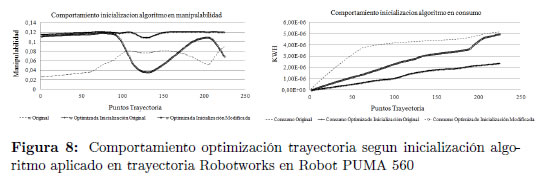
En la Figura 8 se hace una comparación de la optimización obtenida con el algoritmo, aplicada a la trayectoria Robotworks, con la inicialización propia del AHK y con la inicialización modificada. Se aprecia que tanto la manipulabilidad y el consumo eléctrico obtenidos con la inicialización modificada son más óptimos evidenciándose que con la inicialización propia del AHK es posible converger en una solución local.
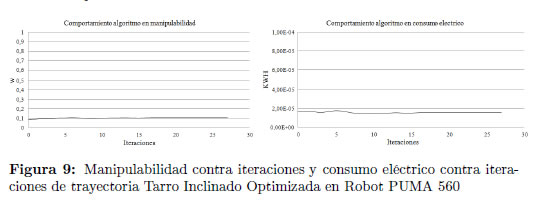
En la Figura 9 se aprecia el comportamiento de la manipulabilidad y del consumo eléctrico a medida que el algoritmo optimiza la trayectoria Tarro Inclinado en cada iteración. En ambos parámetros se cumple con el criterio de paro en la iteración 27.
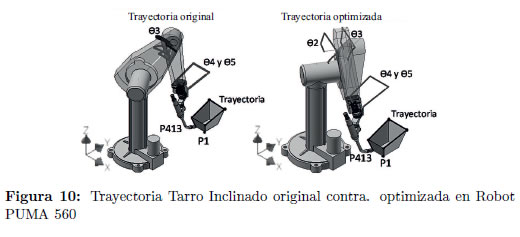
En la Figura 10 se identifican los recorridos que deben hacer las articulaciones del robot PUMA 560 para seguir la trayectoria Tarro Inclinado original y optimizada. Los datos del espacio de trabajo simplificado encontrados por el algoritmo al alcanzar el criterio de paro en la iteración 27 son: Radio = 0.77493786 m, Angulo R: 0.438154 rad y Angulo P: −0.05930750 rad. Estos datos son el punto inicial dentro del espacio de trabajo de la nueva trayectoria optimizada.
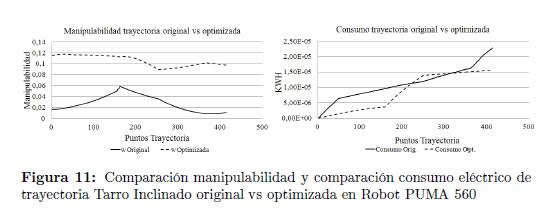
De la Figura 11 se aprecia que la manipulabilidad obtenida con la trayectoria optimizada es mayor y tiende a ser constante a lo largo del recorrido, comparándola con la original, situación que es favorable porque indica un aumento en el desempeño del manipulador en la ejecución de la trayectoria. Adicionalmente se aprecia que el consumo eléctrico final de la trayectoria optimizada es menor comparado con el consumo de la trayectoria original. Sin embargo en el punto 225 de la trayectoria original el consumo de la trayectoria original tendía a ser menor, pero nuevamente en el punto 317 de la trayectoria original el consumo comienza a aumentar superando el de la trayectoria optimizada.
En la Tabla 3 se muestran los valores de los criterios de consumo eléctrico y la manipulabilidad promedio de la trayectoria Tarro Inclinado original y optimizada del robot PUMA 560, evidenciándose que el algoritmo de optimización en la iteración 27 logra optimizaciones del 31.48% en el consumo eléctrico, el 73.02% en la manipulabilidad, incluso del 0.74% en el tiempo de la trayectoria.
4 Conclusiones
En la presente investigación se propone un método multi−objetivo basado en el Algoritmo Heurístico de Kalman, el cual integra simultáneamente la optimización de consumo eléctrico y manipulabilidad, obteniendo una estrategia de planeación de trayectorias para manipuladores seriales antropomórficos de seis grados de libertad y muñeca esférica, usados en procesos soldadura de arco.El método fue validado mediante simulaciones del desplazamiento del manipulador a través de las trayectorias originales y optimizadas almacenadas en hojas de cálculo, que poseen información de los parámetros cinemáticos, diferenciales y dinámicos de cada punto del recorrido que la conforman, y fué implementado en un algoritmo desarrollado en la aplicación de Visual Basic perteneciente al software Autodesk Inventor 2013.
De acuerdo a estos resultados se evidencia que el algoritmo heurístico de Kalman es un método factible para aplicar en la optimización multicriterios de trayectorias presentando ventajas entre las cuales destacan su facilidad de implementación, la demanda de baja memoria y requisitos de velocidad de procesador, y procedimientos de búsqueda basados únicamente en los valores de la función objetivo, sin necesidad de suposiciones fuertes tales como linealidad, diferenciabilidad, convexidad, entre otros. Uno de los inconvenientes detectados con el algoritmo heurístico de Kalman es su convergencia en soluciones locales, pero esto se sorteó modificando la inicialización del algoritmo.
El enfoque de planeación de trayectoria propuesto permite ser usado en cualquier manipulador antropomórfico de seis grados de libertad y muñeca esférica para generar trayectorias optimizadas de acuerdo a los criterios de manipulabilidad y energía eléctrica, conservando la orientación de la herramienta.
El método permite, a partir de cualquier trayectoria planteada en forma de coordenadas cartesianas XYZ y orientaciones del efector en ángulos tipo Euler, buscará una solución óptima posible dentro del espacio de trabajo simplificado del manipulador, no siendo necesario que esta cumpla inicialmente con los límites propios del manipulador.
Una limitante del método es la identificación de los valores de todos los parámetros dinámicos del manipulador comercial necesarios para el cálculo correcto del consumo eléctrico, debido a que los fabricantes solo proporcionan los datos básicos del manipulador. Estos parámetros son propios del diseño del manipulador y sus componentes por lo cual identificarlos es una tarea para la cual se debe contar con las herramientas necesarias para desmantelar el manipulador y cuantificarlos. Sin embargo el método es ideal para ser usado como herramienta de evaluación de parámetros cuando se esté diseñado un manipulador serial antropomórfico de seis grados de libertad y muñeca esférica.
References [ Links ]
[2] A. Lanzutti, ''Smooth Trajectory Planning Algorithms for Industrial Robots: An Experimental Evaluation,'' International journal oJ engineering, vol. 1, pp. 127-132, 2011. [Online]. Available: http://annals.fih.upt.ro/pdf-full/2011/ANNALS-2011-1-18.pdf [ Links ]
[3] T. Yoshikawa, ''Analysis and control of robot manipulators with redundancy,'' Robotics research: the first international ..., pp. 735-737, 1984. [Online]. Available: http://www.engr.colostate.edu/ dga/mech564/handouts/yoshikawa.pdf [ Links ]
[4] T. Urakubo, T. Mashimo, and T. Kanade, ''Optimal placement of a two-link manipulator for door opening,'' 2009 IEEE/RSJ International Conference on Intelligent Robots and Systems, pp. 1446-1451, 2009. [Online]. Available: http://ieeexplore.ieee.org/lpdocs/epic03/wrapper.htm?arnumber=5354076 [ Links ]
[5] S. Mitsi, K.-D. Bouzakis, D. Sagris, and G. Mansour, ''Determination of optimum robot base location considering discrete end-effector positions by means of hybrid genetic algorithm,'' Robotics and Computer-Integrated Manufacturing, vol. 24, no. 1, pp. 50-59, 2008. [Online]. Available: http://linkinghub.elsevier.com/retrieve/pii/S0736584506001025 [ Links ]
[6] R. R. D. Santos, ''Optimal Task Placement of a Serial Robot Manipulator for Manipulability and Mechanical Power Optimization,'' Intelligent Information Management, vol. 02, no. 09, pp. 512-525, 2010. [Online]. Available: http://goo.gl/KjzjqU [ Links ]
[7] R. Ur-rehman, D. Chablat, and P. Wenger, ''Multiobjective Path Placement Optimization of Parallel Kinematics Machines Based on Energy Consumption , Shaking Forces and Maximum Actuators Torques : Application to the Orthoglide,'' Mechanism and Machine Theory, vol. 8, pp. 1125-1141, 2010. [Online]. Available: http://www.sciencedirect.com/science/article/pii/S0094114X10000443 [ Links ]
[8] G. S. Sharma, M. Singh, and T. Singh, ''Optimization of Energy in Robotic arm using Genetic Algorithm,'' InternatIonal Journal of Computer SCIenCe and teChnology, pp. 2009-2011, 2010. [Online]. Available: http://www.ijcst.com/vol22/2/gauri.pdf [ Links ]
[9] Z. Liu, P. Huang, J. Yan, and G. Liu, ''Multi-objective genetic algorithms for trajectory optimization of space manipulator,'' 2009 4th IEEE Conference on Industrial Electronics and Applications, pp. 2810-2815, May 2009. [Online]. Available: http://ieeexplore.ieee.org/lpdocs/epic03/wrapper.htm?arnumber=5138722 [ Links ]
[10] A. Khoukhi, L. Baron, and M. Balazinski, ''Constrained multi-objective trajectory planning of parallel kinematic machines,'' Robotics and Computer-Integrated Manufacturing, vol. 25, no. 4-5, pp. 756-769, 2009. [Online]. Available: http://linkinghub.elsevier.com/retrieve/pii/S0736584508000914 [ Links ]
[11] R. Saravanan, S. Ramabalan, and C. Balamurugan, ''Evolutionary optimal trajectory planning for industrial robot with payload constraints,'' The International Journal of Advanced Manufacturing Technology, vol. 38, no. 11-12, pp. 1213-1226, 2007. [Online]. Available: http://link.springer.com/10.1007/s00170-007-1169-7 [ Links ]
[12] S. Briot and I. A. Bonev, ''Are parallel robots more accurate than serial robots?'' Transactions of the Canadian Society for Mechanical Engineering, vol. 31, no. 4, pp. 445-455, 2007. [Online]. Available: http://www.tcsme.org/Vol31-No4.html [ Links ]
[13] R. Toscano and P. Lyonnet, ''Heuristic Kalman Algorithm for solving optimization problems,'' Systems, Man, and Cybernetics, Part B: ..., pp. 1231-1244, 2009. [Online]. Available: http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=4804686 [ Links ]
[14] T. Yoshikawa, ''Translational and rotational manipulability of robotic manipulators,'' American Control Conference, 1990, no. 8, pp. 1170-1175, 1990. [Online]. Available: http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=4790733 [ Links ]
[15] J. C. Ramírez Henao, J. A. Garzón Jaramillo, and L. Duque Muñoz, ''Manipulability index study on the KUKA robot KR5 ARC HW,'' Signal Processing, and Artificial Vision (STSIVA), 2012 XVII Symposium of Image, pp. 72-77, 2012. [Online]. Available: http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=6340560 [ Links ]
[16] M. W. Spong and M. Vidyasagar, Robot dynamics and control. Wiley. com, 2008. [ Links ]
[17] R. Toscano and P. Lyonnet, ''A new heuristic approach for non-convex optimization problems,'' Information Sciences, vol. 180, no. 10, pp. 1955-1966, May 2010. [Online]. Available: http://www.sciencedirect.com/science/article/pii/S0020025509005714 [ Links ]
[18] B. Armstrong, O. Khatib, and J. Burdick, ''The explicit dynamic model and inertial parameters of the PUMA 560 arm,'' Robotics and Automation. ..., pp. 510-518, 1986. [Online]. Available: http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=1087644 [ Links ]
[19] P. I. Corke, ''In situ Measurement of Robot Motor Electrical Constants,'' Robotica, vol. 14, no. 4, pp. 433-436, 1996. [Online]. Available: http://goo.gl/GwPyxc [ Links ]
[20] Tregaskiss, ''TOUGH GUN G2 Series Robotic MIG Guns.'' 2012. [Online]. Available: http://goo.gl/W3HrGF [ Links ]
[21] Compucraft Ltd, ''RobotWorks - Robotic interface for SolidWorks,'' 1994. [Online]. Available: ttp://www.robotworks-eu.com/products/faq-Kuka.htm [ Links ]