Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería y Ciencia
Print version ISSN 1794-9165
ing.cienc. vol.12 no.23 Medellín Jan./June 2016
https://doi.org/10.17230/ingciencia.12.23.5
ARTÍCULO ORIGINAL
Doi: 10.17230/ingciencia.12.23.5
Neuronal Synchronization of Electrical Activity, using the Hodgkin-Huxley Model and RCLSJ Circuit
Sincronización de la actividad eléctrica neuronal, utilizando el modelo de Hodgkin-Huxley y el circuito RCLSJ
Jose A. Díaz M.1, Oscar Téquita2 and Fernando Naranjo3
1 Universidad Pedagógica y Tecnológica de Colombia, Tunja, Colombia, diazmerchanja@gmail.com.
2 Universidad Pedagógica y Tecnológica de Colombia, Tunja, Colombia, osfateva@hotmail.com.
3 Universidad Pedagógica y Tecnológica de Colombia, Tunja, Colombia, fernando.naranjo@uptc.edu.co.
Received: 08-07-2015 - Accepted: 11-11-2015 - Online: 01-02-2016
MSC:65Z05
Abstract
We simulated the neuronal electrical activity using the Hodgkin-Huxley model (HH) and a superconductor circuit, containing Josephson junctions. These HH model make possible simulate the main neuronal dynamics characteristics such as action potentials, firing threshold and refractory period. The purpose of the manuscript is show a method to syncronize a RCLshunted Josephson junction to a neuronal dynamics represented by the HH model. Thus the RCLSJ circuit is able to mimics the behavior of the HH neuron. We controlated the RCLSJ circuit, using and improved adaptative track scheme, that with the improved Lyapunov functions and the two controllable gain coefficients allowing synchronization of two neuronal models. Results will provide the path to follow forward the understanding neuronal networks synchronization about, generating the intrinsic brain behavior.
Key words: Hodgkin-Huxley model; Josephson junction; Lyapunov function; numerical analysis.
Resumen
Simulamos la actividad eléctrica neuronal mediante el modelo de Hodgkin- Huxley (HH) y un circuito superconductor, que contiene uniones Josephson. El modelo HH simulan las características principales de la dinámica neuronal tales como potenciales de acción, umbrales de disparo y el períodos refractarios. El propósito del manuscrito es mostrar un método para sincronizar un circuito con union Josephson RCLSJ a una dinámica neuronal representado por el modelo HH. Así, el circuito RCLSJ es capaz de imitar el comportamiento de la neurona HH. Controlamos el circuito RCLSJ, utilizando un esquema de control adaptativo, que con funciones de Lyapunov y dos coeficientes de ganancia controlables nos permiten la sincronización de los dos modelos neuronales. Los resultados proporcionan una ruta a seguir adelante en el entendimiento de la sincronización de redes neuronales, generadas por el comportamiento intrinseco del cerebro.
Palabras clave: método modelo de Hodgkin-Huxley; uniones Josephson; funciones de Lyapunov; analisis númerico.
1 Introduction
The synchronization of electrical activity in the brain occurs as the result of interaction among sets of neurons. Neuronal synchronization is defined as correlated appearance in time of two or more events associated with various aspects of neuronal activity at different levels, from single cell to the whole brain. A common scenario involves adjustment or phase locking of rhythms of two or more neurons leading to a stable phase difference of membrane voltage oscillations (periodic or not), e.g., coincidence of action potentials [1].
The neuron is the basic functional unit of the nervous system [2]. In 1952 Alan Lyod Hodgkin and Andrew Huxley studied the behavior of the electrical impulses in squid giant axon. They proposed a system of four nonlinear differential equations and solving these, the solution shows the action potentials behavior, allowing the study of firing threshold and refractory period, which are important electrical characteristics in the neuronal dynamics [3],[4],[5]. The firing threshold is an external stimuli, neccesary for the production of action potential (AP). The refractory period is the temporal lapse after the action potential firing, making hard to fire a second firing [4]. Biophysically, the refractory period is the time that the proteins take from the ionics channels to coming back to their inicial features [3],[4],[6].
Experimental studies show relation between electrical and biological phenomena observed in organisms, allowing observation of a potential difference known as trasmembrane voltage. With the experimental results, Hodgkin and Huxley proposed a biophysical theory that led the construction of their mathematical model [3],[5],[7]. This work made possible the Nobel Prize in medicine in 1963.
When a superconducting device containing Josephson junctions coupled with other electronic devices, due to the complex and the chaotic dynamics, make possible the main characteristic of the neuronal electrical behavior that we were talking above [4],[8].
The Josephson junctions are ssuperconductor's devices separated by a thin insulating barrier which current transport occurs through the Cooper pairs tunnel between the two superconducting electrodes of the junction. Due to its high resolution and low dissipation, are commonly used as effective superconductors devices that allow the construction of sensitive magnetometers.
Interesting results have been discussed obtained by modeling the dynamics of Josephson junctions circuit [9]. For example, McCumber in 1968, built a linear electrical variation of a resistive and capacitive Josephson junction (RCSJ) [10]. Whan et al. [11],[12] studied the characteristics of the I-V curves at different temperatures, noting that if the temperature is increased above 6.6 K, there are some anomalies in the curves I-V attributed to a different nonzero inductance, they also found an extremely rich dynamic behavior RCLSJ circuit by varying the inductance and studied the effect of thermal noise on the circuit RCLSJ. Mazo at al. [13] studied the dynamic of thermal depinning of fluxon in discrete Josephson regular ring.
We used the RCLSJ circuit (resistively, capacitively, inductively shunted Josephson junctions) and using an adaptive improved synchronization scheme, we found a function that allows the two neuronal models synchronization and reproduce the neuronal behavior observed by Hodgking and Huxley [14].
In Figure 1, show a diagram circuit RCLSJ where RS is the resistance due to the leak, C is the junction capacitance, L is the inductance and R(V) is the resistance of the Josephson junction. This circuit reproduce the neuronal electrical activity [8],[10],[15].
In this work we controlled the RCLSJ circuit for simulate the dynamic properties of the neuronal model showed by Hodgking and Huxley, obtaining coupling function using an improved adaptive track scheme, and this could be understood like the synchronization between two different dynamical system.
Neurons are morphologically different, however, neurons have complete synchronization or generalized synchronization [8]. We focus on generalized synchronization between the Hodgking-Huxley model and the RCLSJ circuit, because complete synchronization is part of this.
We introduce gain coefficients in the Lyapunov functions for a set of synchronization transitory periods. Using this method, we estimate analytically the controller that will allow synchronization between the two models [9] . Getting to know synchronization mechanisms will advance the construction of more complex neural networks.
2 Mathematical model
The model of Hodgkin-Huxley contains four nonlinear ordinary differential equations that describe the generation and propagation of action potentials. Due to the fact these equations have no exact solution, makes necessary to use the numerical methods, in this case, fourth order Runge-Kutta method to solve them [3],[7],[16],[17].

These Equations (1) represent the Hodgkin-Huxley model. Where V is the potential, I is the current per unit area, gi is the maximal value of the conductance (i = Na; k;L).n; m; h are dimensionless quantities between 0 and 1 that are associated with potassium channel activation, sodium channel inactivation, respectively. Using the voltage clamp and the space clamp methods, they measured quantitatively axon ionic current and their research allow to stablish a system of four ordinary differential Equations (1) including the following support functions [3],[5].

Hodgkin-Huxley found values of constants experimentally [3],[5]. Their magnitudes are given by (3):


Now, our research focus on the RCLSJ circuit and Hodgkin-Huxley model synchronization process, and calculating a controller, to study the behavior for different system conditions.
The dynamic equations adimensionales RCLSJ model are (4):

Where the voltage  , the phase difference
, the phase difference  y and the induced current
y and the induced current  can be studied by introducing a DC external force, changing the bifurcation parameter [15],[17].
can be studied by introducing a DC external force, changing the bifurcation parameter [15],[17].
Values for the circuit parameters, proposed McCumber [10] are βL = 2:6, βC = 0:707 [4,11]; applied external current DC is i=80 mA. The nonlinear damping term g( ) is approximated with a currente-voltage relation represented as follows [12],[15],[17]:
) is approximated with a currente-voltage relation represented as follows [12],[15],[17]:

Due to the different structural organizations of the two nonlinear systems, we require a controller. We introduce the system controller for the circuit.

Where u is the controller that is calculated using Lyapunov functions [4]. In this study, the system is controlled to simulate neuronal firing from de Hodgkin-Huxley model to RCLSJ circuit, it means, we mapped the junction voltage of RCLSJ to produce an approximation to mapping the membrana voltage in Hodgkin-Huxley system.
The error of the corresponding variables is denoted by (7):

We introduce the following positive Lyapunov function with two gain coefficients as follows [8],[9],[14],[18]

Where α and β gain coefficient are positive and the sum of the variance error of the series in Equation (9) shows the degree of synchronization.

The error function shown in Equation (7) it can be stabilized for certain values where the output variables v and  coincide, which shows the type of synchronization between the two systems. According to the theory of Lyapunov, the errors of the corresponding variables can be stabilized to a certain threshold and the two systems achieve synchronization one [19].
coincide, which shows the type of synchronization between the two systems. According to the theory of Lyapunov, the errors of the corresponding variables can be stabilized to a certain threshold and the two systems achieve synchronization one [19].
When the derivative of the Lyapunov function in (7) is completely negative, as follows:

Simplifying Equation (11) we obtain the condition negative error dynamic equation

In accordance with (12, 13), the two gain coefficient plays a role similar the convergence rate of the Lyapunov function to approximate stability. With the conditions of Equation (12), the linearization v = K + C, and the Equation (7). Thus, the controller is denoted by (14):
+ C, and the Equation (7). Thus, the controller is denoted by (14):

Changing the values for the constants (K, C) we find generalized synchronization. We find that for K = 1 and C = 0 you get full synchronization.
3 Numerical simulation and results:
We simulate the HH-RCLSJ model synchronization using the Runge-Kutta method fourth order with h = 0.001 to calculate the nonlinear equations time series. We selected gain coefficients to control the RCLSJ system (6) and synchronize with the Hodgkin-Huxley model (1). The initial values of the system variables RCLSJ controller shown in (6) are (0.5, 0.6, 0.9) [4],[11]. The initial conditions of the Hodgking-Huxley model are: n=0.31768, h=0.59612, m=0.052932.
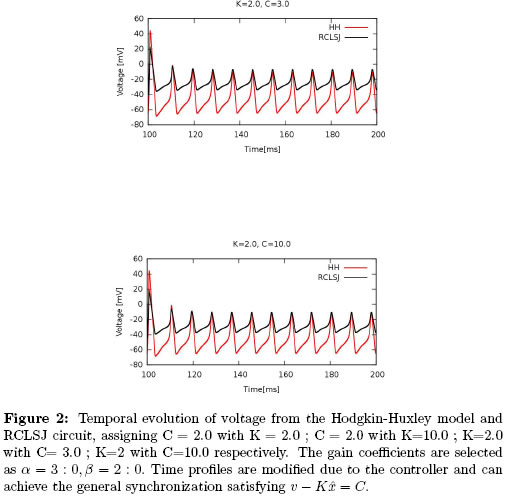
Also, we calculate the time profile for action potentials in the RCLSJHH model under different conditions to understand C and K to understand generalized synchronization.
The Figure 2 shows that the output series of the two system change their amplitudes for certain values. Furthermore that the two spikes trains spikes can be linearized voltage (v -  = C) to achieve the generalized synchronization [8].
= C) to achieve the generalized synchronization [8].
Finally, the specific case K=1 and C=0 represents the complete synchronization problem, Figure 4.
The degree of synchronization between the two models may be seen neuronal considering the error function (7). We can observe in above Figures 2 and 3 that the Refractory Period is independent the gain coefficients α and β, and the constant values K and C. We can obtain that the refractory period value is approximately 8.75 ms.
Initially, neurons respond in a altered form, but when the system is stabilized; syncrhonization is achieved in the train of action potentials in response to the applied current system.
The Figure 4 shows the two types of synchronization; complete and widespread. In addition, the amplitudes are compared by varying parameters K and C. Considering the results of the synchronization pattern with the Hodgkin-Huxley model and the RCLSJ circuit using the controller obtained by the improved adadtive track scheme, we can infer that the system includes RCLSJ circuit when the controller reproduces the dynamic action potentials of cell due to the passage of sodium, potassium and other ion channels to generate the trans membrane potential.
4 Conclusions
We obtain via Lyapunov functions a controller for the RCLSJ circuit that simulate the dynamic properties of Hodgkin-Huxley neuronal model, based on generalized synchronization. The controller was found analytically using Hodgkin-Huxley model and RCLSJ circuit with the inclusion of two gain coefficient that may be varied. Some interesting results are:
1. Depending on the gain coefficient value, acceleration improve the synchronization process.
2. To find a generalized synchronization, we define the function v = K  +C and we found that: for K = 1 and C = 0 complete synchronization is reached, which is a specific case of the generalized synchronization.
+C and we found that: for K = 1 and C = 0 complete synchronization is reached, which is a specific case of the generalized synchronization.
With the results, we can control the dynamic behavior of the RCLSJ system to reproduce neuronal electrical behavior of Hodgkin-Huxley model. The synchronization of these two models could show a path towards to construct large networks of neurons using the RCLSJ circuit due superconductivity.
Acknowledgements
This work was supported by Grupo de Física Teórica y computacional, Universidad Pedagógica y Tecnológica de Colombia.
References
[1] I. Timofeev, M. Bazhenov, J. Seigneur, and T. Sejnowsk, "Neuronal Synchronization and Thalamocortical Rhythms in Sleep, Wake and Epilepsy, Jasper's Basic Mechanism of the Epilepsies," 1974. [Online]. Available: http://www.ncbi.nlm.nih.gov/books/NBK50785/ 94 [ Links ]
[2] C. Hammond, "Cellular and molecular neurobiology," Ph.D. dissertation, Academic Press, Great Britain, 1996. 94 [ Links ]
[3] A. L. Hodgkin and A. F. Huxley, "A quantitative description of membrane current and its application to conduction and excitation in nerve," The Journal of Physiology, vol. 117, no. 4, pp. 500-544, 1952. [Online]. Available: http://dx.doi.org/10.1113/jphysiol.1952.sp004764 95, 97 [ Links ]
[4] P. Crotty, D. Schult, and K. Segall, "Josephson junction simulation of neurons," Phys. Rev. E, vol. 82, p. 011914, Jul 2010. [Online]. Available: http://link.aps.org/doi/10.1103/PhysRevE.82.011914 95, 99, 101 [ Links ]
[5] A. L. Hodgkin and A. F. Huxley, "Currents carried by sodium and potassium ions through the membrane of the giant axon of loligo," The Journal of Physiology, vol. 116, no. 4, pp. 449-472, 1952. [Online]. Available: http://dx.doi.org/10.1113/jphysiol.1952.sp004717 95, 97 [ Links ]
[6] M. Carolina Barriga, C. Humberto Carrillo, and L. Fernando Ongay, "El modelo de Fitzhugh-Nagumo para el potencial eléctrico de una neurona," 2003. [Online]. Available: http://mmc.geofisica.unam.mx/acl/integra/Manual-Tutoriales/FHN.pdf 95 [ Links ]
[7] D. Aaby, M. Usma, and A. Singh, "A Comparative Study of Numerical Methods for the Hodgkin-Huxley Model of Nerve Cell Action Potentials." 95, 97 [ Links ]
[8] F. Li, Q. Liu, H. Guo, Y. Zhao, J. Tang, and J. Ma, "Simulating the electric activity of fitzhugh-nagumo neuron by using josephson junction model," Nonlinear Dynamics, vol. 69, no. 4, pp. 2169-2179, 2012. [Online]. Available: http://dx.doi.org/10.1007/s11071-012-0417-z 95, 96, 99, 101 [ Links ]
[9] L. H. Nguyen and K.-S. Hong, "Synchronization of coupled chaotic fitzhughnagumo neurons via lyapunov functions," Mathematics and Computers in Simulation, vol. 82, no. 4, pp. 590 - 603, 2011. [Online]. Available: http://www.sciencedirect.com/science/article/pii/S0378475411002540 95, 96, 99 [ Links ]
[10] D. McCumber, "Effect of ac inpedance on dc voltage-current characteristics of a superconductor weak-link junction," J. Appl. Phys, vol. 39, no. 3113, pp. 6157-6181, 1968. [Online]. Available: http://dx.doi.org/10.1063/1.1656743 95, 96, 98 [ Links ]
[11] C. Whan, C. Lobb, and M. Forrester, "Effect of inductance on externally shunted Josephson tunnel junctions," J. Appl. Phys., vol. 77, no. 382, 1995. [Online]. Available: http://dx.doi.org/10.1063/1.359334 95, [ Links ] 101
[12] C. Whan and C. Lobb, "Complex dynamical behavior in rcl-shunted josephson junctions," Applied Superconductivity, IEEE Transactions on, vol. 5, no. 2, pp. 3094-3097, June 1995. 95, 98 [ Links ]
[13] J. Mazo, F. Naranjo, and K. Segall, "Thermal depinning of fluxons in discrete Josephson rings," Physical Review B, vol. 78, no. 17, 2008. 95 [ Links ]
[14] M. Jun, H. Long, X. Zhen-Bo, and C. Wang, "Simulated test of electric activity of neurons by using josephson junction based on synchronization scheme," Communications in Nonlinear Science and Numerical Simulation, vol. 17, no. 6, pp. 2659 - 2669, 2012. [Online]. Available: http://www.sciencedirect.com/science/article/pii/S1007570411005995 96, 99 [ Links ]
[15] S. Dana, D. Sengupta, and C.-K. Hu, "Spiking and bursting in josephson junction," Circuits and Systems II: Express Briefs, IEEE Transactions on, vol. 53, no. 10, pp. 1031-1034, Oct 2006. 96, 98 [ Links ]
[16] D. Sterratt, B. Graham, A. Gillies, and D. Willshaw, Principles of computational modelling in neuroscience. Cambridge University Press, 2011. 97 [ Links ]
[17] Y. t Hu, T. g Zhou, J. Gu, S. l Yan, L. Fang, and X. j Zhao, "Study on chaotic behaviors of rclsj model josephson junctions," Journal of Physics: Conference Series, vol. 96, no. 1, p. 012035, 2008. [Online]. Available: http://stacks.iop.org/1742-6596/96/i=1/a=012035 97, 98 [ Links ]
[18] M. Aqil, K.-S. Hong, and M.-Y. Jeong, "Synchronization of coupled chaotic fitzhugh-nagumo systems," Communications in Nonlinear Science and Numerical Simulation, vol. 17, no. 4, pp. 1615 - 1627, 2012. [Online]. Available: http://www.sciencedirect.com/science/article/pii/S1007570411005363 99 [ Links ]
[19] S. H. Strogatz, Nonlinear dynamics and chaos: with applications to physics, biology, chemistry, and engineering. Westview press, 2014. 99 [ Links ]


















