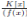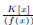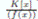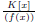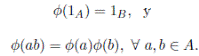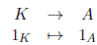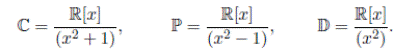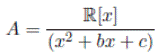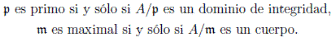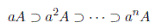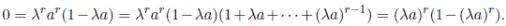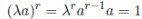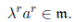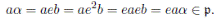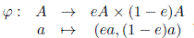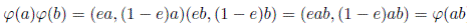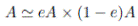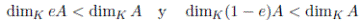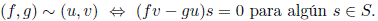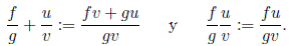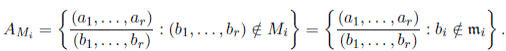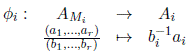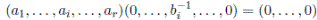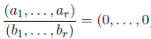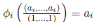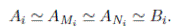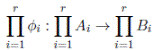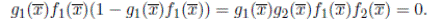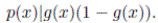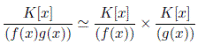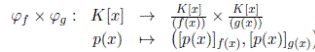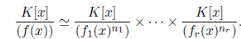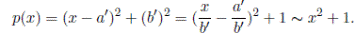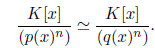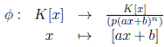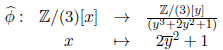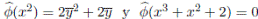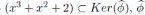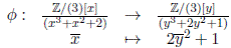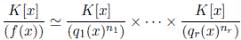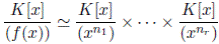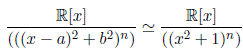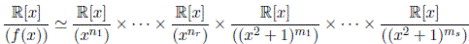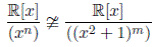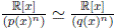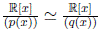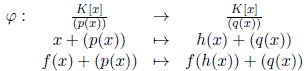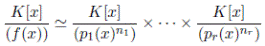1 Introducción
Sea K un cuerpo. Una K−álgebra A con unidad es un conjunto dotado de dos operaciones (A,+, ·) cumpliendo que:
1. es un anillo con unidad
2. es un K−espacio vectorial
3. para todo α ∈ K y para todos a, b ∈ A, α(ab) = (αa)b = a(αb).
Decimos que A es una K−álgebra finita si es una K−álgebra conmutativa con unidad y de dimensión finita como K−espacio vectorial. Denotaremos por dimK A a su dimensión como K−espacio vectorial.
Un homomorfismo de K−álgebras es una aplicación lineal 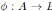 entre dos K−álgebras tal que
entre dos K−álgebras tal que
El homomorfismo structural
es inyectivo ya que K es cuerpo. Por lo tanto 1 K es parte libre en el K−espacio vectorial A y puedo extender {1 A } a una base de A.
Si dim K A = 2, tomamos γ ∈ A \ K, luego {1 A, γ} es parte libre en A y por tanto {1 A, γ} es una base del K−espacio vectorial A. Además como 1 · γ = γ · 1, se tiene que el anillo A es conmutativo. Sin embargo, para dimensiones superiores, las K−álgebras no son necesariamente conmutativas. Por ejemplo, el cuerpo de los números cuaterniónicos es una R−álgebra de dimensión cuatro que no es conmutativa. En este artículo estamos interesados sólo en K−álgebras conmutativas.
Las K−álgebras finitas han sido un tema de investigación permanente en álgebra conmutativa, ver por ejemplo 1), (2), (3) y (4. Nosotros presentamos aquí un estudio sistemático y con menos teoría especializada de ellas en comparación con las encontradas en los textos tradicionales de álgebra conmutativa 5), (6), (7), (8) y (9.
Las K−álgebras son usadas en áreas muy diversas como representaciones de grupo, teoría de códigos, la ecuación de Yang-Baxter, álgebras de Hopf y las álgebras de Frobenius 10. Las K−álgebras no sólo son importantes en matemáticas, también encontramos en la literatura que se usan en otras áreas principalmente cuando el cuerpo K es el de los números complejos. Por ejemplo, las C∗−álgebras son fundamentales en física cuántica. En 11 y 12 se estudian algunas C∗−álgebras de dimensión finita donde se amplían resultados que se interpretan en mecánica cuántica. Además, en 13 y 14 se caracterizan ciertas C∗−álgebras cuyos resultados son relevantes para los fundamentos de la teoría cuántica.
Existen, salvo isomorfismos, tres álgebras de dimensión 2 sobre R:
Esto es debido a que en una extensión de grado 2 de R,
se pueden dar tres casos según x 2 + bx + c tenga dos raíces imaginarias, dos raíces reales distintas o una raíz doble. Los conjuntos C, P, D son, respectivamente, los números complejos, los números paracomplejos y los números duales, 2.
La teoría de funciones complejas es más estudiada que las otras dos. Algebraicamente, esto refleja el hecho de que C es un cuerpo, mientras que P y D no lo son pues P tiene divisores de cero y D tiene además elementos nilpotentes.
Las rectas proyectivas sobre las R−álgebras C, P, D generan las tres geometrías clásicas del plano, Moebius, Laguerre y Minkowski, ver 15. En general es poco lo que se conoce sobre las rectas proyectivas sobre las K−álgebras finitas. En 16 y 17 se estudió la interpretación proyectiva de estas métricas del plano real y en 1 se hizo una clasificación de todas las R−álgebras finitas. 18 es un trabajo reciente sobre la geometría co rrespondiente a la R−álgebra tridimensional
rrespondiente a la R−álgebra tridimensional 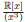 pero en general estudiar la geometría sobre R−álgebras finitas es un problema abierto.
pero en general estudiar la geometría sobre R−álgebras finitas es un problema abierto.
Iniciamos este artículo probando que las K−álgebras finitas son suma directa de K−álgebras finitas locales. Luego mostramos que toda K−álgebra finita se descompone en forma única, salvo isomorfismos, en suma directa de K−álgebras finitas locales. Seguidamente caracterizamos la K−álgebra
finita local , mostramos que ciertas K−álgebras finitas son isomorfas y descomponemos la K−álgebra finita 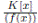 en K−álgebras finitas locales.
en K−álgebras finitas locales.
2 K−algebras finitas
Sea A una K−álgebra finita. Un ideal p es primo si p ƒ= (1) y si ab ∈ p entonces a ∈ p o b ∈ p y un ideal m es maximal si m ƒ= (1) y no existe ningún ideal a tal que m ⊂ a ⊂ (1). Esto es equivalente a decir:
Por tanto un ideal maximal es primo pero el recíproco no es cierto en general. El ideal cero es primo si y sólo si A es un dominio entero. Cada elemento de A que no es unidad está contenido en un ideal maximal 5.
A toda K−álgebra finita A podemos asociar un espacio topológico llamado el espectro primo de A, Spec(A), que consiste en el conjunto de todos sus ideales primos. También asociamos a A el espacio Max(A) que consiste en el conjunto de todos los ideales maximales de A. Existen K−álgebras finitas con exactamente un ideal maximal, por ejemplo, el cuerpo de los números complejos 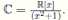 Una K−álgebra finita A que tiene exactamente un ideal maximal se llama K−álgebra finita local.
Una K−álgebra finita A que tiene exactamente un ideal maximal se llama K−álgebra finita local.
Sea Σ un subconjunto parcialmente ordenado por una relación ≤. Las siguientes condiciones en Σ son equivalentes, (5):
Cada sucesión creciente x1 ≤ x2 ≤ ... en Σ es estacionaria (es decir, existe n tal que xn = xn+1 = ...).
Cada subconjunto no vacío de Σ tiene un elemento maximal.
Si Σ es el conjunto de submódulos de un módulo M , ordenado por la relación ⊆, entonces (i) se denomina la condición de cadena ascendente y (ii) la condición maximal. Un módulo M que satisface una de estas dos condiciones equivalentes se denomina noetheriano (de Emmy Noether). Si Σ está ordenado por ⊇, entonces (i) es la condición de cadena descendente y (ii) la condición minimal. Un módulo M que satisface una de estas dos condiciones equivalentes se denomina artiniano (de Emil Artin).
Toda K−álgebra finita A es artiniana y noetheriana, ver (5). En la Proposición 2.2 vamos a obtener un primer resultado de estructura para este tipo de K−álgebras. Una prueba de esta proposición resulta como consecuencia del teorema de estructura de anillos de Artin, ver [5, Teorema 8.7]. Nosotros presentamos una demostración distinta y con menos teoría especializada. Para esto primero demostramos el Lema 2.1. Decimos que e ∈ A es idempotente si e2 = e.
Lema 2.1. Si A es una K−álgebra artiniana, entonces A es local si y sólo si los únicos idempotentes de A son 0 y 1.
Demostración. ⇒: Si A es una K−álgebra local de ideal maximal 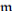 y e ∈ A es idempotente, entonces
e2
= e. Luego, e −
e2
= e(1 − e) = 0 y tenemos dos casos:
y e ∈ A es idempotente, entonces
e2
= e. Luego, e −
e2
= e(1 − e) = 0 y tenemos dos casos:
(i) Si e ∈ 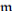 entonces 1 − e ∈/
entonces 1 − e ∈/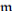 . Como A es local, 1 − e es inversible luego e(1 − e)
. Como A es local, 1 − e es inversible luego e(1 − e)
(1 − e) −1 = 0 y por tanto e = 0.
(ii) Si 1 − e ∈ 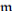 entonces e ∈/
entonces e ∈/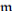 . Como A es local, e es inversible entonces e (1 − e)e−1 = 0. Por tanto 1 − e = 0 y e = 1.
. Como A es local, e es inversible entonces e (1 − e)e−1 = 0. Por tanto 1 − e = 0 y e = 1.
⇐: A es artiniana y sus únicos idempotentes son 0 y 1, sea 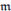 un ideal maximal de A y sea a ∈ A con a ∈/
un ideal maximal de A y sea a ∈ A con a ∈/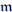 . Si a es no inversible, aA es un ideal propio de A entonces
. Si a es no inversible, aA es un ideal propio de A entonces
es una sucesión decreciente de ideales y como A es artiniana, A es estacionaria. Luego existe r tal que arA = ar+1A entonces ar ∈ ar+1A y existe λ ∈ A tal que ar = λar+1. Por tanto, ar(1 − λa) = 0 y
Entonces (λa)r es idempotente. Pero los únicos idempotentes de A son 0 y 1. Si
tenemos que a es inversible y esto es una contradicción. Si (λa)r = 0, entonces
Como a ∈/ m, λr ∈ 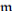 pero
pero 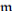 es primo luego λ ∈
es primo luego λ ∈ 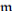 . Lo cual es un absurdo pues ar(1 − λa) = 0 implica que 1 − λa ∈
. Lo cual es un absurdo pues ar(1 − λa) = 0 implica que 1 − λa ∈ 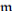 por tanto λ ∈/
por tanto λ ∈/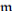 .
.
En consecuencia, para todo a ∈ A tal que a ∈/ 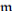 tenemos que a es inversible y A es local.
tenemos que a es inversible y A es local.
Proposición 2.2. A es una K−álgebra finita si y sólo si A es una suma directa de K−álgebras finitas locales.
Demostración. ⇒: Si dimK A = 1 como K−espacio vectorial, A ≃ K luego A es local. Si dimK A > 1 y no tiene mas idempotentes que 0 y 1, por el Lema 2.1, A es una K−álgebra local finita. En caso contrario, existe e ∈ A idempotente, e ƒ= 1 y e ƒ= 0. Entonces
(i) eA es un subanillo de A ya que eA es un ideal y por tanto es subanillo. Además el uno de eA es e pues e(ea) = e 2 a = ea, para todo ea ∈ eA.
(ii) Todo ideal de eA es ideal de A. En efecto, sea  ideal de eA luego para todo α ∈
ideal de eA luego para todo α ∈  y para todo a ∈ A se cumple que eaα ∈
y para todo a ∈ A se cumple que eaα ∈  . Note que α = eb, b ∈ A. Entonces
. Note que α = eb, b ∈ A. Entonces  es ideal de A porque para todo α ∈
es ideal de A porque para todo α ∈  y para todo a ∈ A, se tiene que
y para todo a ∈ A, se tiene que
Además, como A es artiniana, eA es artiniana ya que cualquier sucesión decreciente de ideales de eA es una sucesión decreciente de ideales de A y por tanto estacionaria.
(iii) eA y (1 − e)A son subespacios vectoriales de A y e(1 − e) = 0 entonces para todo a ∈ A, a = ea + (1 − e)a luego A = eA + (1 − e)A suma como K−espacios vectoriales. Además si β ∈ eA∩(1−e)A, β = ea = (1−e)b para a, b ∈ A entonces β = ea = e 2 a = e(1 − e)b = 0.
En consecuencia, A es suma directa de eA y (1 − e)A como K−espacios vectoriales y tenemos el isomorfismo de K−espacios vectoriales
Tomando en eA × (1 − e)A la estructura product
pues 1 − e es también idempotente. Luego
como K−álgebras.
Puesto que eA y (1 − e)A son subespacios no nulos y dimK A es finita, se tiene que
es decir las dimensiones de eA y (1 − e)A son menores que la dimensión de A.
Si eA y (1 − e)A no tienen más elementos idempotentes que 0 y 1, por el Lema 2.1, eA y (1 − e) A son K−álgebras locales finitas. De lo contrario y como las dos álgebras son de dimensión menor que la de A seguimos el proceso inductivamente hasta obtener el resultado deseado.
⇐: Se comprueba sin dificultad.
En el ítem (ii) de la demostración de la Proposición 2.2, observe que si p ∈ Spec(eA), no necesariamente p ∈ Spec(A). Por ejemplo, sea A = R3 y e = (1, 1, 0) entonces eA = {(a, b, 0) : a, b ∈ R}. Un ideal primo de eA es m eA = {(a, 0, 0) : a ∈ R} y m eA no es ideal primo en A pues (0, 1, 0) y (0, 0, 1) no pertenecen a m eA y su producto es cero.
Consideremos la K−álgebra finita 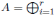 Ai donde cada Ai es una K−álgebra finita local con ideal maximal Mi, i = 1, . . . , r. El Lema 2.3 presenta un isomorfismo entre cada Ai y el correspondiente anillo de fracciones o localización AMi , Mi ∈ Max(A), definido a continuación:
Ai donde cada Ai es una K−álgebra finita local con ideal maximal Mi, i = 1, . . . , r. El Lema 2.3 presenta un isomorfismo entre cada Ai y el correspondiente anillo de fracciones o localización AMi , Mi ∈ Max(A), definido a continuación:
Diremos que un subconjunto S del anillo A es un sistema multiplicativo cuando 1 ∈ S y s, t ∈ S ⇒ st ∈ S. Se define en A × S la relación de equivalencia
En el conjunto cociente AS := A × S/ ∼ denotamos a la clase de equivalencia de (f, g) como 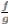 y se definen las operaciones suma y producto como si fueran fracciones de Q:
y se definen las operaciones suma y producto como si fueran fracciones de Q:
Estas operaciones están bien definidas y hacen de AS un anillo conmutativo  con unidad, donde el cero es
con unidad, donde el cero es 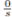 , para s ∈ S y la unidad es
, para s ∈ S y la unidad es 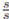 , para s ∈ S. Más aún, se tiene un homomorfismo canónico de anillos
, para s ∈ S. Más aún, se tiene un homomorfismo canónico de anillos 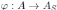 dado por
dado por 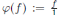 que en general no es inyectivo. Al anillo AS le llamamos anillo de fracciones o localización de A por S.
que en general no es inyectivo. Al anillo AS le llamamos anillo de fracciones o localización de A por S.
Lema 2.3. Sea 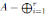 Ai
una K−álgebra finita donde cada Ai
es una K−álgebra local finita. Para i = 1, . . . , r sea
Ai
una K−álgebra finita donde cada Ai
es una K−álgebra local finita. Para i = 1, . . . , r sea 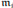 el ideal maximal de Ai
. Entonces
el ideal maximal de Ai
. Entonces
(1) Max(A) = {M1, . . . , Mr} donde 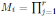 mj
con mj
= Aj, para todo
mj
con mj
= Aj, para todo 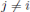 y
y 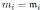 .
.
(2) Para todo i = 1, . . . , r se tiene que AMi ≃ Ai.
Demostración. (1) Es consecuencia de que los ideales maximales de una suma directa de r anillos tienen la forma Mi para todo i = 1, ..., r. Ver (1, Lema 1.2.6).
(2) Para todo i = 1, . . . , r,
Como Ai es local, bi es inversible y la aplicación
es un homomorfismo de anillos. Note que φi es inyectiva ya que si bi-1ai = 0, entonces existe 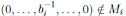 tal que
tal que
y esto equivale a que
para 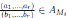 Además, φi
es sobreyectiva porque, para todo ai
∈ Ai,existe
Además, φi
es sobreyectiva porque, para todo ai
∈ Ai,existe 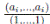
La siguiente proposición muestra que una K−álgebra finita se descompone en forma única, salvo isomorfismos, en suma directa de K−álgebras finitas locales.
Proposición 2.4. Sean 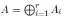 y
y 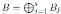 dos K−álgebras finitas donde Ai, Bj
son K−álgebras locales finitas. Entonces A ≃ B como K−álgebras si y sólo si r = s y, después de reordenar los Bj
, para todo i = 1, . . . , r se tiene que Ai
≃ Bi
como K−álgebras.
dos K−álgebras finitas donde Ai, Bj
son K−álgebras locales finitas. Entonces A ≃ B como K−álgebras si y sólo si r = s y, después de reordenar los Bj
, para todo i = 1, . . . , r se tiene que Ai
≃ Bi
como K−álgebras.
Demostración. ⇒: Como 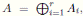 por el Lema 2.3, Max(A) = {M
1
, . . . , Mr
} y para todo i = 1, . . . , r se tiene AMi
≃ Ai. Además, por hipótesis,
por el Lema 2.3, Max(A) = {M
1
, . . . , Mr
} y para todo i = 1, . . . , r se tiene AMi
≃ Ai. Además, por hipótesis, 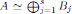 luego por el Lema 2.3, Max(A) = {N
1
, . . . , Ns
} y para todo j = 1, . . . , s se tiene ANj
≃ Bj
. Entonces para todo i, existe j tal que Mi
= Nj
. Por tanto después de reordenar a los Bj, para todo i = 1, . . . , r,
luego por el Lema 2.3, Max(A) = {N
1
, . . . , Ns
} y para todo j = 1, . . . , s se tiene ANj
≃ Bj
. Entonces para todo i, existe j tal que Mi
= Nj
. Por tanto después de reordenar a los Bj, para todo i = 1, . . . , r,
⇐: Si para todo i = 1, . . . , r se tiene que 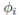 es el isomorfismo entre Ai
y Bi
, entonces
es el isomorfismo entre Ai
y Bi
, entonces
es un isomorfismo.
En consecuencia, por la Proposición 2.4, estudiar la estructura de las K−álgebras finitas se reduce a estudiar la estructura de las K−álgebras locales finitas.
3 Caracterizaciones e isomorfismos
El ejemplo más simple de las K−álgebras finitas es el de las K−álgebras 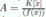 caracterizadas porque existe u ∈ A tal que 1
, u, . . . , un-1
es base de A como K−espacio vectorial. Obviamente no toda K−álgebra finita esde este tipo, por ejemplo
caracterizadas porque existe u ∈ A tal que 1
, u, . . . , un-1
es base de A como K−espacio vectorial. Obviamente no toda K−álgebra finita esde este tipo, por ejemplo  ya que todo elemento al cuadrado de esta álgebra es cero, luego no puede existir u ∈ A tal que 1, u, u
2 sea base de A
ya que todo elemento al cuadrado de esta álgebra es cero, luego no puede existir u ∈ A tal que 1, u, u
2 sea base de A
como K−espacio vectorial.
Lema 3.1. La K−álgebra finita 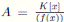 es local si y sólo si existe p(x) ∈ K(x), polinomio irreducible, tal que f (x) = p(x)n. En este caso su ideal maximal es
es local si y sólo si existe p(x) ∈ K(x), polinomio irreducible, tal que f (x) = p(x)n. En este caso su ideal maximal es 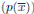 y el cuerpo residual es
y el cuerpo residual es  .
.
Demostración. Los elementos de 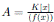 se escriben de forma única como
se escriben de forma única como 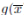 con g(x) ∈ K[x] y grado(g) <grado(f ).
con g(x) ∈ K[x] y grado(g) <grado(f ).
⇒: Si f (x) no es potencia de un irreducible, en particular f (x) no es irreducible, entonces f (x) = f 1(x)f 2(x) donde mcd(f 1 , f 2) = 1 por tanto existen g 1 , g 2 ∈ K(x) tales que g 1 f 1 + g 2 f 2 = 1 luego 1 − g 1 f 1 = g 2 f 2 y
Enconsecuencia, 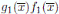 es idempotente y que
es idempotente y que 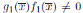 y
y 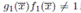 . Pues de lo contrario, si
. Pues de lo contrario, si 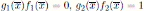 es decir
es decir 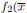 es inversible pero esto es absurdo pues
es inversible pero esto es absurdo pues 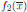 es un divisor de cero de A. Por la misma razón
es un divisor de cero de A. Por la misma razón 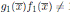 . Usando el Lema 2.1 tenemos que A no es local y esto es una contradicción que proviene de suponer que f no es irreducible.
. Usando el Lema 2.1 tenemos que A no es local y esto es una contradicción que proviene de suponer que f no es irreducible.
⇐: Si g(x) ∈ A es idempotente entonces 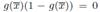 y esto equivale a que p(x)
n
divide a g(x)(1 − g(x)) luego
y esto equivale a que p(x)
n
divide a g(x)(1 − g(x)) luego
Por tanto, p(x)|g(x) o p(x)|(1−g(x)) pero no a los dos a la vez pues p(x) ∤ 1. Si p(x)|g(x) entonces p(x) ∤ (1−g(x)) y por tanto p(x)
n
|g(x) luego 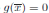 y si p(x)|(1 − g(x)) entonces p(x) ∤ g(x) y por tanto p(x)n|(1 − g(x)) luego
y si p(x)|(1 − g(x)) entonces p(x) ∤ g(x) y por tanto p(x)n|(1 − g(x)) luego 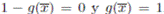 . En consecuencia, por el Lema 2.1, A es local. Además como p(x) es irreducible, el ideal (p(x)) es maximal y contiene a (p(x)
n
). Luego
. En consecuencia, por el Lema 2.1, A es local. Además como p(x) es irreducible, el ideal (p(x)) es maximal y contiene a (p(x)
n
). Luego 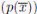 es el ideal maximal de A y su cuerpo residual es
es el ideal maximal de A y su cuerpo residual es 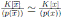 .
.
Lema 3.2. Sean f (x), g(x) ∈ K[x] tales que mcd(f, g) = 1. Entonces existe un isomorfismo de K−álgebras
dotando al producto cartesiano de estructura de K−álgebra con las operaciones suma y producto componente a componente.
Demostración. Para todo f (x) ∈ K[x], sea 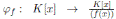 el ho momorfismo natural definido por
el ho momorfismo natural definido por 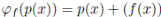 . Entonces
. Entonces
es homomorfismo de K−álgebras y 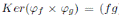 ya que h ∈
ya que h ∈ 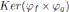 si y sólo si h ∈
si y sólo si h ∈ 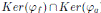 y
y 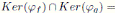
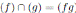 pues mcd(f, g) = 1. Además,
pues mcd(f, g) = 1. Además, 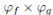 es sobreyectiva. En efecto, sea
es sobreyectiva. En efecto, sea 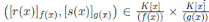 , como f y g son primos entre si, existen c
1
, c
2 ∈ K[x] tales que c
1
f + c
2
g = 1, en
, como f y g son primos entre si, existen c
1
, c
2 ∈ K[x] tales que c
1
f + c
2
g = 1, en 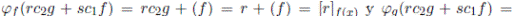
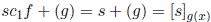 .
.
La proposición siguiente presenta la descomposición en productos de K−álgebras locales y se demuestra usando iterativamente la prueba del Lema 3.2.
Proposición 3.3. Si 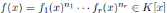 es un producto de factores irreducibles distintos entonces
es un producto de factores irreducibles distintos entonces
Lema 3.4. (1) Un homomorfismo de K−álgebras 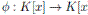 queda unívocamente determinado por
queda unívocamente determinado por 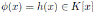 .
.
(2) 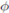 es un isomorfismo de K−álgebras si y sólo si
es un isomorfismo de K−álgebras si y sólo si 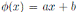 con a, b ∈ K y a ƒ= 0.
con a, b ∈ K y a ƒ= 0.
Demostración. (1) Se sigue de que todo homomorfismo de álgebras está caracterizado por lo que le hace a sus generadores, en este caso a x.
(2) Es inmediato, pues todo isomorfismo de K[x] en K[x] preserva la graduación.
Definición 3.5. p(x) es equivalente a q(x), p(x) ∼ q(x), si y sólo si existen a, b ∈ K con a ƒ= 0 tales que q(x) = p(ax + b).
Proposición 3.6. (1) Si K = R, entonces los polinomios irreducibles de K(x) son equivalentes a x o x 2 + 1.
(2) Si K es algebraicamente cerrado, entonces para todo p(x) irreducible, p(x) ∼ x.
Demostración. (1) En R[x], los polinomios irreducibles son lineales de la forma p(x) = ax + b con a ƒ= 0 o de grado dos de la forma ax 2 + bx + c con b 2 − 4ac < 0. Si p(x) = ax + b con a ƒ= 0, por definición, p(x) ∼ x. Además, note que ax 2 + bx + c con b 2 − 4ac < 0 es equivalente a que p(x) = (x − a′)2 + (b′)2 con b′ ƒ= 0. Luego,
(2) Si K es algebraicamente cerrado, los polinomios irreducibles p(x) son lineales y por definición, p(x) ∼ x.
Lema 3.7. Sea n ∈ N. Si p(x) ∼ q(x) entonces
Demostración. Como p(x) ∼ q(x), existen a, b ∈ K con a ƒ= 0 tales que q(x) = p(ax + b). Sea φ el homomorfismo
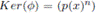 ya que para
ya que para 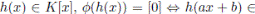
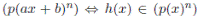 . Además,
. Además, 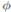 es sobreyectiva. Sea
es sobreyectiva. Sea 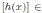
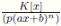 , por el Lema 3.4, existe ˜h(x) ∈ K[x] tal que h(x) = ˜h(ax + b) entonces
, por el Lema 3.4, existe ˜h(x) ∈ K[x] tal que h(x) = ˜h(ax + b) entonces 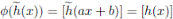 .
.
El recíproco del Lema 3.7 no es cierto incluso bajo la hipótesis de que p(x) y q(x) sean irreducibles como lo prueba el ejemplo siguiente.
Ejemplo 3.8. Sean A = 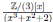 y
y 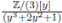 . Entonces
. Entonces 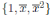 y
y 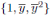 son bases de A y B respectivamente como espacios vectoriales. Definimos el homomorfismo de álgebras
son bases de A y B respectivamente como espacios vectoriales. Definimos el homomorfismo de álgebras
Veamos que φ es un isomorfismo. En efecto, 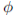 es inyectivo ya que si
es inyectivo ya que si 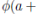
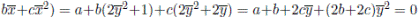 entonces a+b = 0, c = 0 y b+c = 0. Luego a = b = c = 0 y
entonces a+b = 0, c = 0 y b+c = 0. Luego a = b = c = 0 y 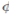 es inyectiva. Puesto que las álgebras tienen la misma dimensión, como espacios vectoriales, entonces se tiene el isomorfismo
es inyectiva. Puesto que las álgebras tienen la misma dimensión, como espacios vectoriales, entonces se tiene el isomorfismo 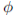 .
.
Observe que x3 + x2 + 2 ≁ y3 + 2y2 + 1 ya que no existe una transformación lineal que lleve un polinomio en el otro.
Corolario 3.9. (1) Si 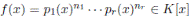 es producto de factores irreducibles distintos y pi
(x) ∼ qi
(x) para todo i = 1, . . . , r entonces
es producto de factores irreducibles distintos y pi
(x) ∼ qi
(x) para todo i = 1, . . . , r entonces
(2) En particular, si 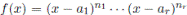 y K es algebraicamente cerrado entonces
y K es algebraicamente cerrado entonces
Demostración. (1) Se tiene por la Proposición 3.3 y el Lema 3.7.
(2) Puesto que x − ai ∼ x y por el item (1) tenemos el isomorfismo.
Corolario 3.10. Sea K = R.
Si n ∈ N y a, b ∈ R con b ƒ= 0 entonces
 (2) Si f (x) ∈ R(x) entonces existen n
1
, . . . , nr, m
1
, . . . , ms
tales que
(2) Si f (x) ∈ R(x) entonces existen n
1
, . . . , nr, m
1
, . . . , ms
tales que
Demostración. (1) Puesto que (x − a)2 + b 2 ∼ x 2 + 1, por el Lema 3.7 tenemos el isomorfismo.
(2) Por la Proposición 3.6, existen n
1
, . . . , nr, m
1
, . . . , ms
∈ R tales que 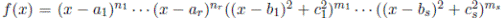 y por la Proposición 3.3 y el item (1) se sigue el resultado.
y por la Proposición 3.3 y el item (1) se sigue el resultado.
Observe que se presenta el problema de la unicidad de la descomposición. En el caso de cuerpos algebraicamente cerrados la descomposición es única y queda determinada por los números n
1
, . . . , nr
es decir para todo f (x) ∈ K[x] existen n
1
, . . . , nr
únicos con 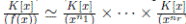 . En el caso real la situación es la misma como veremos mas adelante.
. En el caso real la situación es la misma como veremos mas adelante.
Lema 3.11. Para todos m, n enteros positivos,
Demostración. Por el Lema 3.1, el cuerpo residual de la R−álgebra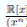 es
es 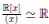 y el cuerpo residual de
y el cuerpo residual de 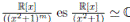 . Luego las álgebras no son isomorfas.
. Luego las álgebras no son isomorfas.
Lema 3.12. Si p(x) y q(x) son elementos irreducibles de R(x) las condiciones siguientes son equivalentes:
(1) p(x) ∼ q(x).
Demostración. (1) ⇒ (2) Se tiene por el Lema 3.7.
⇒ (3) Inmediato tomando n = 1. Entonces 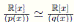
(3) ⇒ (1) Puesto que p(x) y q(x) son irreducibles en R(x) entonces 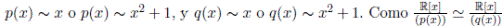 y en virtud del Lema 3.11, tenemos dos casos:
y en virtud del Lema 3.11, tenemos dos casos:
(i) p(x) ∼ x y q(x) ∼ x, entonces p(x) ∼ q(x).
(ii) p(x) ∼ x2 + 1 y q(x) ∼ x2 + 1, entonces p(x) ∼ q(x).
En consecuencia, para f (x) ∈ R(x), existen n1, . . . , nr, m1, . . . , ms únicos tales que 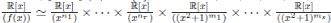 . En el caso general lo que se puede decir es que:
. En el caso general lo que se puede decir es que:
Lema 3.13. Sean p(x) y q(x) elementos irreducibles de K[x]. Para todo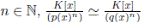 si y solo si
si y solo si 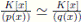
Demostración. ⇒: Por el Lema 3.1, 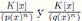 son álgebras locales con cuerpos residuales
son álgebras locales con cuerpos residuales 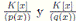 respectivamente. Además como
respectivamente. Además como 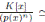
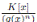 entonces
entonces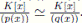
⇐: Sea
Por el Lema 3.1, 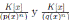 son álgebras locales con cuerpos residuals
son álgebras locales con cuerpos residuals 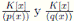 , y con ideales maximales
, y con ideales maximales 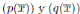 respectivamente. Por hipótesis
respectivamente. Por hipótesis  es un isomorfismo, es decir los cuerpos residuales de las álgebras locales son isomorfos y por tanto los ideales maximales también lo son. En consecuencia
es un isomorfismo, es decir los cuerpos residuales de las álgebras locales son isomorfos y por tanto los ideales maximales también lo son. En consecuencia 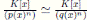 .
.
El ejemplo 3.8 muestra que K[x]/(p(x)) ≃ K[x]/(q(x)) no implica que p(x) ∼ q(x) entonces la descomposición que puede obtenerse f (x) = 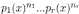 en componentes irreducibles induce un isomorfismo
en componentes irreducibles induce un isomorfismo
pero p 1(x), . . . , pr (x) no están unívocamente determinados salvo transformaciones lineales.
4 Conclusiones
Las K−álgebras finitas, es decir las K−álgebras conmutativas conunidad de dimensión finita como K−espacio vectorial, han sido un tema muy estudiado en álgebra conmutativa, ver por ejemplo 1), (2), (3) y 4, y en este artículo hemos hecho un estudio sistemático y sencillo de ellas en comparación con los encontrados en los textos tradicionales de álgebra conmutativa 5), (6), (7), (8 y 9. Iniciamos probando que las K−álgebras finitas son suma directa de K−álgebras locales finitas. Luego caracterizamos la K−álgebra local finite 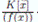 , mostramos que ciertas K−álgebras finitasson isomorfas e hicimos una descomposición de la K−álgebra finite
, mostramos que ciertas K−álgebras finitasson isomorfas e hicimos una descomposición de la K−álgebra finite 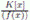 en K−álgebras locales finitas.
en K−álgebras locales finitas.
Las K−álgebras son usadas en áreas muy diversas como representaciones de grupo, teoría de códigos, la ecuación de Yang-Baxter, álgebras de Hopf y las álgebras de Frobenius (10). Las K−álgebras no sólo son importantes en matemáticas, también se usan en otras áreas. Por ejemplo, las C∗−álgebras son fundamentales en física cuántica. En (11), (12), (13) y (14) se estudian algunas C∗−álgebras donde se amplían resultados que se interpretan en la teoría cuántica.
Las rectas proyectivas sobre las R−álgebras finitas de dimensión dos, 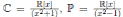 y
y 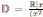 generan las tres geometrías clásicas del plano, Moebius, Laguerre y Minkowski, ver 15. 18 es un trabajo reciente sobre la geometría correspondiente a la R−álgebra tridimensional pero en general estudiar la geometría sobre las R−álgebras finitas es un problema abierto.
generan las tres geometrías clásicas del plano, Moebius, Laguerre y Minkowski, ver 15. 18 es un trabajo reciente sobre la geometría correspondiente a la R−álgebra tridimensional pero en general estudiar la geometría sobre las R−álgebras finitas es un problema abierto.