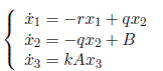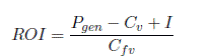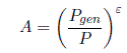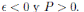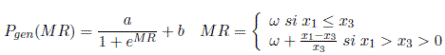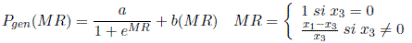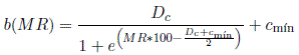1 Introducción
Gran parte de los esfuerzos de investigación se centran en el análisis y clasificación de esquemas de modelado y simulación de sistemas 1),(2),(3. En consecuencia, existe una amplia discusión acerca de qué tipo de modelado o nivel de agregación se debe utilizar para abstraer las características de la realidad. Algunos puntos en común de quienes intentan definir esta cuestión giran en torno a que el modelado y análisis dependen de las necesidades del modelador, los fenómenos que intenta representar y los resultados que espera analizar 4.
Para estudiar los sistemas en el caso particular de este artículo se parte de un modelado en dinámica de sistemas 5),(6. Además, se utiliza la teoría clásica para analizar sistemas dinámicos y suaves a trozos, y estudiar sus resultados de manera cualitativa 2),(7. Igualmente se tiene presente el papel que juega dicho análisis para los esquemas que se plantean en dinámica de sistemas. El objetivo de este trabajo es mostrar cómo utilizando la teoría clásica que ofrecen los sistemas dinámicos para realizar el análisis cualitativo de un modelo de mercado de electricidad, basado en dinámica de sistemas, se pueden explotar resultados adicionales del modelado.
El concepto de cualitativo ha tenido diferentes connotaciones en el campo del modelado. Se esperaría que la información contenida en los diagramas causales tenga esta naturaleza 2. Ese no es el significado de cualitativo que se discute. El término cualitativo hace referencia a los diferentes fenómenos que un sistema exhibe, es decir, las tendencias de su flujo dinámico a lo largo del tiempo. Por ejemplo, cuando en el sistema, una variable de nivel se incrementa, decrece, presenta oscilaciones o llega a un punto de equilibrio. Y, además, si dicha dinámica está determinada por un parámetro en específico (puntos de apalancamiento) o conjunto de reglas de decisión que la afectan 8, condiciones de frontera, discontinuidades, entre otros.
La dinámica de sistemas está estructurada de manera que cuenta con una parte de modelado matemático y otra que se centra en los métodos numéricos de simulación. Por lo mismo, un modelo basado en dinámica de sistemas es un objeto matemático 9. De ahí que merezca un análisis matemático de su dinámica. Ya algunos trabajos se han adelantado al respecto. Ejemplo de ello es la investigación de J. Redondo, 10, en donde plantea, que es posible modelar el mercado eléctrico colombiano explorando las ecuaciones del modelo que fue expresado mediante un sistema suave a trozos. Se refuerza dicho planteamiento ya en un primer acercamiento al tema, en un trabajo previo, que permite modelar un mercado eléctrico nacional utilizando un sistema de ecuaciones diferenciales suaves por tramos y aplicar los criterios de estabilidad en el mismo 11), (12. Es posible ver en otros campos, cómo los sistemas dinámicos híbridos y suaves a trozos son cada vez más utilizados en ingeniería y en ciencias aplicadas para modelar una amplia variedad de sistemas físicos y dispositivos tecnológicos. Dentro de los ejemplos se incluyen sistemas mecánicos con impactos y fricción, robots caminantes, redes genéticas, convertidores electrónicos de potencia, sistemas híbridos de control, sistemas con saturaciones, sistemas económicos, sistemas sociales y, más en general, todos los sistemas y dispositivos cuya dinámica se ve afectada por la ocurrencia de eventos discontinuos 13),(14. Aunque es de aclarar que, en sistemas económicos, estos esquemas se utilizan en menor medida 15.
Para el estudio de sistemas dinámicos suaves a trozos, existen diferentes herramientas analíticas, numéricas y experimentales 12. Es por eso que la verificación y comparación de los resultados entre cada una de las estrategias se hace necesaria. Es muy común utilizar modelos continuos para describir sistemas dinámicos discontinuos. Sin embargo, tales modelos continuos pueden no proporcionar predicciones adecuadas de las dinámicas discontinuas. Para entender mejor los sistemas discontinuos, se debe ser consciente de que modelos discontinuos proporcionarán una adecuada y explicación. Por lo tanto, considerar un sistema global discontinuo consiste en tener varios sub-sistemas continuos en diferentes dominios. Cada sub-sistema continuo posee propiedades dinámicas diferentes, es decir, reglas de evolución para cada sub-sistema continuo adyacente. Debido a esta capacidad de cambio, las leyes de transición a través de las fronteras deben ser estudiadas con mayor detalle. Dentro del proyecto de investigación en el que está enmarcado este trabajo se han encontrado algunos resultados que próximamente serán publicados 11. Dichas variaciones pueden conducir a cambios drásticos en el comportamiento dinámico del sistema. Se ha demostrado, por ejemplo, que la transición al caos, con frecuencia, es debida a las bifurcaciones inducidas por las discontinuidades (cambios abruptos) en las fronteras con las cuales se modela el sistema.
La complementariedad entre dinámica de sistemas y el análisis matemático, con la ayuda de la teoría moderna de los sistemas dinámicos no lineales, permite establecer el comportamiento cualitativo. Sin embargo, a veces, resulta difícil distinguir entre lo cualitativo y lo cuantitativo. Por ello, partiendo de un esquema mental, que es fundamentalmente la raíz de la dinámica de sistemas, es posible alcanzar de manera clara modelos cuantitativos que describan el sistema en cuestión. De esta forma, es posible utilizar esquemas de modelado no lineales de sistemas suaves a trozos o discontinuos (PWS de sus siglas en ingles Piece-Wise Smooth), que representan en alto grado los fenómenos presentes en situaciones reales. Es así cómo la dinámica de sistemas permite, con alto nivel de detalle, estudiar
fenómenos sustancialmente complejos, que a la larga no son más que en un conjunto de sistemas suaves a trozos, interconectados cuidadosamente mediante funciones o leyes matemáticas. Los modelos basados en dinámica de sistemas son la traducción de un tipo de modelo mental en el lenguaje de sistemas dinámicos 2.
De lo anterior, resulta que existe una amplia gama de estrategias para modelar y simular mercados eléctricos. Sin embargo, en lo que se refiere a la explotación de dichos modelos, son menores los aportes, quizá por los intereses mismos de quienes realizan los trabajos de investigación. Quienes están interesados en seguir la escuela de Sterman y Forrester, se limitan a los criterios de expertos y a los resultados que arrojan los paquetes de simulación diseñados con ese propósito. Y del otro lado, debido a la complejidad de las ecuaciones diferenciales y a la manera de formularlas, quienes modelan mercados nacionales de electricidad están en busca de comportamientos complejos que, para algunos casos reales del mercado, no pasan de ser una novedad matemática. Por lo mismo, surge entonces la necesidad de integrar ambas metodologías, ya que para mercados nacionales de electricidad aún queda mucho camino por recorrer y un gran número de dinámicas por explorar.
Se propone entonces un trabajo como el que sigue, donde, a continuación, el lector se encontrará con una síntesis metodológica, por completo basada en pensamiento sistémico, que se resume en definición del problema, conceptualización, formulación y evaluación o explotación de los modelos. Una manera de trabajo ya propuesta por Aracil y Sterman en sus libros 2), (3. En estos trabajos, para algunos casos es posible estudiar el sistema dinámico, calibrar el modelo, realizar simulaciones y análisis de sensibilidad, para finalmente explorar escenarios de políticas. Si bien mediante ecuaciones diferenciales es posible realizar dicho trabajo, resulta complejo interpretar o proponer un conjunto de ecuaciones que modelen adecuadamente un mercado nacional de electricidad. Se acostumbra, luego de que aparece el sistema dinámico, a encontrar los puntos de equilibrio del mismo, determinar su estabilidad, realizar retratos de fase, construir diagramas de bifurcación y estudiar los comportamientos transitorios o los comportamientos invariantes en el tiempo.
Es entonces de gran importancia la estructura metodológica de ambas estrategias en un solo camino de aprovechamiento del modelo. Esto, porque utilizando dinámica de sistemas y la teoría clásica de sistemas dinámicos para representar los comportamientos de mercados eléctricos, incluso se pueden establecer las tendencias dinámicas del sistema bajo la variación de parámetros, permitiendo la construcción de un mapa con todos los escenarios posibles del sistema, cómo ya en algún momento lo planteo 10. Ello, además de la identificación de los parámetros que afectan significativamente el comportamiento del mismo, y definir los puntos de apalancamiento del mercado.
Para explorar esta estrategia, se resume en la siguiente sección cada una de las partes de la síntesis metodológica y, a continuación, en un caso de estudio, se muestra cada uno de los pasos para modelar un mercado eléctrico nacional con una tecnología de generación. Finalmente, se intenta aprovechar al máximo ese modelo y se establecen las conclusiones que se obtienen de dicho análisis y del trabajo de investigación.
2 Síntesis Metodológica
En la Figura 1 se muestra la síntesis metodológica que se propone para realizar el modelado, simulación y análisis de un mercado de electricidad. Dicho planteamiento surge después de hacer una revisión sistemática de la literatura, e indica el modo en el que se procede para integrar de manera complementaria la dinámica de sistemas y el análisis dinámico. Ya en 1989 Sterman plantea, en uno de sus trabajos 16, cómo se puede estudiar la aparición de caos determinístico en un modelo experimental de economía basado en pensamiento sistémico. Análogamente, es posible evidenciar en los primeros trabajos de Aracil 17, cómo de manera sistemática se parte de un modelo basado en dinámica de sistemas y se llega finalmente al estudio de ecuaciones diferenciales 2.
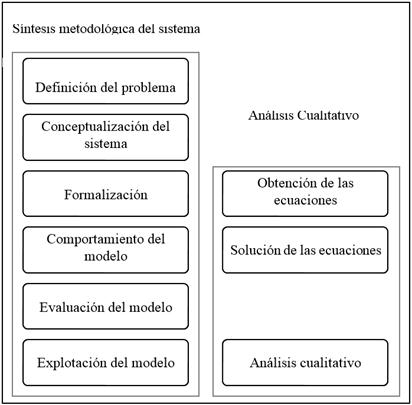
Figura 1: Mapa metodológico que resume los principales apartados de manera sistemática para dinámica de sistemas y sistemas dinámicos.
Para escribir la síntesis metodológica que aquí se propone, se consideran los esquemas metodológicos que plantea Aracil en su documento de Dinámica de Sistemas9. En él se muestra de manera general cómo, desde un esquema mental y utilizando la teoría del pensamiento sistémico, es posible aprovechar un modelo basado en dinámica de sistemas. Además, se tiene el libro de Sterman Business Dynamics3, en donde es posible identificar diferentes herramientas y métodos sistémicos para validar y evaluar un modelo. Este último con una motivación ciertamente empresarial.
Estos planteamientos son aplicables al modelado basado en sistemas dinámicos y, aunque aún no se ha escrito una síntesis en que estos se integren para establecer una metodología, la manera en que se plantean, analizan y finalmente se explotan los modelos, arroja resultados complementarios. Es decir, de la revisión sistemática en la manera en que estos autores modelan y aprovechan los modelos, se evidencia la síntesis aquí descrita. Cabe anotar que dicho proceso no es estrictamente secuencial y, como en todo proceso de modelado, es iterativo. A continuación, se hace una breve descripción de cada fase de la metodología que integra la Dinámica de Sistemas y Análisis Dinámico.
Definición del problema: en esta primera etapa, se plantean una serie de relaciones causales que reflejan la influencia de los diferentes componentes del sistema que se quiere estudiar. Por ejemplo, cómo el incremento o decremento de una variable podría afectar otras variables del sistema, y qué tipo de las mismas se deben incluir en el modelo. En esta fase, todo parte de un esquema mental.
Conceptualización del sistema: en esta fase, se propone plantear el diagrama de influencias del sistema y, evidenciar de manera concreta cómo las hipótesis planteadas del esquema mental influyen en la dinámica del modelo. Ello da lugar al diagrama causal.
Formalización: luego de que se cuenta con un diagrama causal, es posible obtener el diagrama de flujos y niveles o de Forrester. Para ello se utiliza un paquete computacional que al final permitirá observar un modelo programado por computador. Para esta etapa, existen varios paquetes comerciales y queda a criterio del modelador utilizar uno u otro. Adicionalmente, se facilita la obtención de las ecuaciones. El diagrama de flujos y niveles es de por sí un objeto matemático y, como tal, puede representarse mediante un conjunto de ecuaciones diferenciales. Existen algunos tipos de software que permiten de manera automática ver las ecuaciones que describen el modelo, pero por simple inspección se convierte en una tarea ardua entender la lista de ecuaciones que estos paquetes arrojan. Por lo anterior, se sugiere escribir el arreglo matemático a manera de sistema de ecuaciones diferenciales, en donde por definición, las variables de nivel, son las variables de estado del sistema. De forma adicional, es posible detectar en el sistema de ecuaciones el grado de complejidad dinámico del mismo, es decir, qué tan suave o no suave es, cuáles funciones son discontinuas y qué relaciones entre las variables es posible modelar nuevamente.
Comportamiento del modelo: en dinámica de sistemas, esta etapa del modelado consiste en realizar la simulación numérica del modelo y explorar las trayectorias del mismo. Para el usuario, es transparente la manera en cómo el paquete de simulación soluciona las ecuaciones, aunque, en algunos casos, es posible personalizar el método de integración y parámetros del mismo. De forma paralela es posible encontrar la solución del sistema de ecuaciones. En esta etapa surgen varias opciones relacionadas con el grado de complejidad del sistema de ecuaciones que se extrajeron en la fase anterior. Por ejemplo, puede que sea posible contar con una solución anaítica de dicho sistema o, por el contrario, se debe utilizar algún método de integración numérica para solucionarlo. De igual manera, se debe escoger un esquema de simulación, que permita representar adecuadamente el flujo dinámico a través del tiempo, de dicha solución.
Evaluación del modelo (o validación del modelo): tanto para los modelos basados en dinámica de sistemas como para representaciones mediante ecuaciones diferenciales en sistemas dinámicos, esta etapa es de crucial importancia. Aquí es cuando se someten a diferentes pruebas, que garantizan su validez y utilidad. Por tanto, hay diferentes maneras de hacerlo, pero, en esencia, el objetivo es que exista coherencia lógica entre los resultados numéricos y las trayectorias, con las hipótesis planteadas. Para el caso de dinámica de sistemas, se apela al criterio de expertos, así como en sistemas dinámicos se busca que haya consistencia dimensional en las unidades y los resultados obtenidos de las ecuaciones. También, se realizan los ajustes pertinentes de los parámetros y se evalúa de nuevo la pertinencia de los resultados con la realidad. Otra manera posible es evaluar, en cualquiera de los dos casos, con valores extremos, garantizando su funcionamiento. Por lo mismo, se realiza un análisis de sensibilidad numérica.
Explotación del modelo: normalmente, en dinámica de sistemas, es en esta fase cuando se evalúan políticas aplicadas al modelo estudiado, y el efecto que estas generan o qué escenarios plantean. Se realiza análisis de sensibilidad en el comportamiento o en las políticas. Y, para aprovechar más ampliamente el modelo hasta el momento obtenido. Se puede entonces hacer un enfoque en el análisis cualitativo. En algunos casos, los modelos planteados no poseen la riqueza dinámica que podría esperarse; pero, en contrapartida, el análisis cualitativo ofrece a la dinámica de sistemas una explotación mayor del modelo. Este planteamiento surge motivado por la necesidad de reconocer los parámetros y su influencia directa en el sistema modelado. Es decir, qué tan estables o inestables son las soluciones del sistema, de qué manera están los parámetros asociados a las oscilaciones que se aprecian en algunas trayectorias y, reforzar o refutar los argumentos de las políticas y los escenarios que se pueden presentar en el modelo que se esté estudiando.
3 Caso de estudio: un mercado de electricidad nacional
Como se planteó en la sección anterior, se sugiere que mediante dicha síntesis metodológica es posible aprovechar los modelos de mercados eléctricos nacionales. Aunque están basados en dinámica de sistemas, se puede aprovechar la teoría de sistemas dinámicos para obtener y explotar modelos sustancialmente agregados, que representan en gran medida el comportamiento del mercado. A continuación, se realiza el modelado, análisis, simulación y explotación de un caso particular.
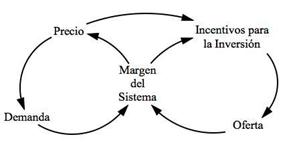
Definición del problema: se asume entonces, cinco variables principales que afectan el comportamiento de un mercado nacional de electricidad. Ya en el trabajo presentado por Dyner et al, en el 2000 18), (19, se definió la estructura de un mercado nacional de electricidad a partir de su oferta y su demanda. Igualmente, se definió entonces el margen de reserva del sistema como el puente que une la oferta con la demanda y permite medir los efectos sobre el precio que esta señal tendría. De acuerdo a la Figura 2, es posible entender dicho mercado, como cualquier otro mercado en el que la disponibilidad medida a través del margen de reserva afecte el precio y la inversión en el sistema.
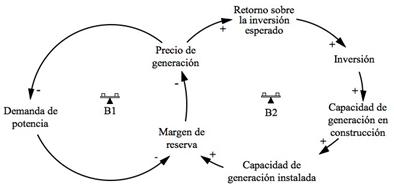
Figura 3: Diagrama causal que reúne las hipótesis dinámicas, para el comportamiento de un mercado de electricidad nacional. (Fuente los autores)
Conceptualización del sistema: la Figura 3 representa el diagrama de influencias o causal de cada una de las variables incluidas en el mercado nacional de electricidad. Se tienen entonces dos ciclos de balance, el ciclo B1 y el ciclo B2, que no son más que el lado de la demanda y el lado de la oferta, respectivamente. Mediante este planteamiento, dependiendo del margen de reserva, que afecta significativamente el precio de generación del sistema, se realizan inversiones para suplir la demanda. Se debe garantizar un margen de reserva positivo, pues, de lo contrario, habría racionamiento de electricidad. Esto se traduce en que si el margen de reserva es pequeño, su relación con el precio es inverso, porque se a cerca una escasez y, al contar con un precio de generación alto, los operadores podrán invertir en la planta de generación.
Formalización: luego de conceptualizar el mercado nacional de electricidad se formula el diagrama de Forrester, también conocido como diagrama de flujos y niveles.
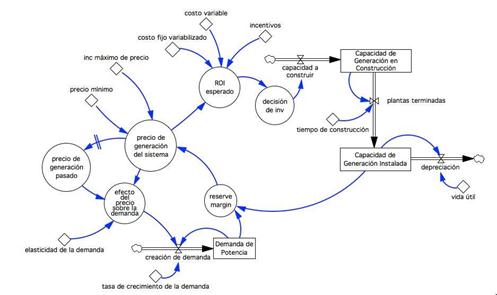
Figura 4: Diagrama de flujos y niveles que permite simular el comportamiento de un mercado nacional de electricidad.
En el diagrama de flujos y niveles de la Figura 4, se muestran tres variables de nivel, representadas por el rectángulo, también conocidas como variables de estado. También se muestran las variables auxiliares, correspondientes a cada uno de los círculos, que permiten establecer los flujos dinámicos entre cada una de las variables de nivel. La capacidad a construir se modela como una función suave por tramos, en la que dependiendo el retorno sobre la inversión esperado, se responde a las necesidades del sistema. Cabe aclarar que, cuando se construye, existe un tiempo de retardo dependiendo de la tecnología de generación. Este es un retardo de primer orden, donde el sistema, en general, recibe la información de cuánto se está construyendo. Debido a las no suavidades que pueden incluirse además en la decisión de inversión, es necesario explorar las implicaciones de las mismas. El precio de generación del sistema hace referencia al precio neto que se le paga a los generadores después de realizada la inversión. Dependiendo del país y la tecnología, la manera en que se modela el precio podría variar.
Sistema de ecuaciones: como el diagrama de la Figura 4 es, de hecho, un objeto matemático, es posible escribir el sistema de ecuaciones diferenciales que representa el mercado nacional de electricidad como se muestra en la Ecuación (1). Ver 2), (11), (12. Donde x˙ i , con i = 1, 2, 3, son las variables de estado del sistema.
En donde, la capacidad de generación instalada es x1, la capacidad de generación en construcción x 2 y la demanda de potencia x 3. B es la capacidad a construir, definida por una función no suave escalonada, que depende de la decisión de inversión Dinv = max {0, ROI} y,
con r, q y Cfv > 0; k ∈ R e I > 0.
A se define como el efecto del precio sobre la demanda de potencia. Finalmente, el precio de generación es Pgen y MR es el margen de reserva del sistema que mide la relación entre la oferta y la demanda (para ambos se tendrá una expresión funcional más adelante).
Debido a que el interés de este documento no es precisar sobre las ecuaciones, queda, ciertamente, un amplio abanico de comportamientos y análisis por realizar. Dicho trabajo da lugar a otros resultados concretos (11). Para cumplir con ese propósito, se recurre a la teoría clásica de la dinámica no lineal y la teoría de modelamiento de sistemas suaves por tramos.
Comportamiento del modelo: ahora es posible explorar el flujo dinámico del mercado. Se puede utilizar un paquete de simulación como Vensim o PowerSim, y para resolver el sistema de ecuaciones, se puede utilizar un esquema numérico basado en eventos e implementado en Matlab. Lo primero a verificar es que, sin importar el modo de simulación, los resultados sean aproximadamente iguales, difiriendo entre sí por el integrador o el método utilizado. Además, dependiendo de los análisis que se deseen realizar, se recurre a una herramienta u otra.
Del análisis de estabilidad del sistema de ecuaciones diferenciales presentado en Ecuación (1), se encontró que, en términos generales, la estabilidad del sistema depende de la tasa de crecimiento de la demanda. Dicho valor se encuentra alrededor del 3 % o 4 % anual, y está descrito por el parámetro k. Para Colombia, el promedio es del 3 %, mientras que en algunos países europeos, es del −1 %. Se puede comprobar que, si la tasa de crecimiento de la demanda es positiva, el sistema es inestable, presentando un crecimiento exponencial de la variable de estado asociada a la demanda.
En cambio, si la tasa es negativa, la demanda tiende a cero. Además, para valores de la tasa cercanos a cero, el número de oscilaciones se incrementa (15). Este último comportamiento, a modo de ejemplo, se puede apreciar en las Figuras 5 y 6.
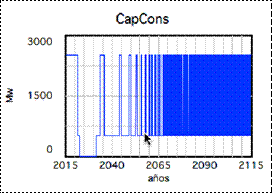
Figura 5: Comportamiento del sistema con una tasa de crecimiento de la demanda cercana a cero, k ≈ 0, para la capacidad de generación en construcción.
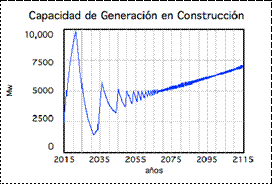
Figura 6: Comportamiento del sistema con una tasa de crecimiento de la demanda cercana a cero, k ≈ 0, para la capacidad a construir.
Evaluación del modelo: existen tres casos de análisis de sensibilidad que son de interés en los modelos basados en dinámica de sistemas: sensibilidad numérica, sensibilidad en el modo de comportamiento y sensibilidad ante la implementación de políticas. En esta etapa de la metodología interesa explorar la sensibilidad numérica, ya que es en este momento cuando se realizan los ajustes necesarios que permiten verificar los planteamientos iniciales.
La sensibilidad numérica existe cuando cambios en los supuestos, cambian los resultados numéricos. Por ejemplo, cambiando la elasticidad de la realimentación boca a boca en un modelo de difusión de nuevas tecnologías, la tasa de crecimiento del nuevo producto puede cambiar. Sterman, en su libro dice que "Todos los modelos exhiben sensibilidad numérica" (3).
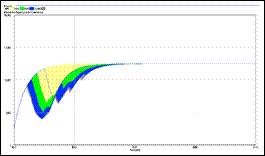
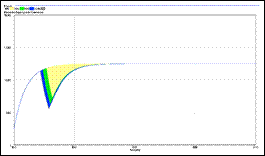
Este tipo de análisis es simplemente numérico; es decir, no se observan fácilmente modos de sensibilidad en dichas gráficas. Por ello, solamente se pueden apreciar las tendencias del mercado, en toda la ventana de simulación, en los casos hipotéticos planteados. Para llevar a cabo este análisis de sensibilidad numérico se tomó una ventana para la tasa de crecimiento de la demanda entre −0,04 y 0,04, utilizando el método Montecarlo que está incluido en el paquete de simulación VensimPlus. Ver Figuras 7, 8 y 9. Vale la pena mencionar que la distribución para realizar la prueba fue uniforme, garantizando una variación del parámetro acorde a las necesidades de los resultados.
Explotación del modelo: cuando los patrones de comportamiento varían al cambiar los supuestos del modelo, se habla de sensibilidad en el modo del comportamiento. Esto se da, por ejemplo, cuando, frente a alternativas, el modelo deja de presentar comportamientos oscilatorios y pasa a presentar comportamientos monótonos. Es posible entonces utilizar las herramientas que consigo trae VensimPlus o algún otro tipo de software basado en dinámica de sistemas, pero la información que se obtiene del mismo es limitada. Por ello, se propone utilizar mapeos asíncronos de Poincaré. El Asynchronous Switching Map o A-Switching Map es una herramienta normalmente utilizada en el análisis de sistemas dinámicos para estudiar los comportamientos complejos que sistemas físicos reales puedan presentar, como en el análisis de convertidores de potencia (13).
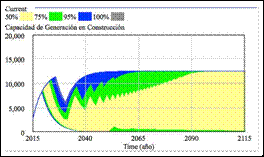
Figura 7: Análisis de sensibilidad numérica, cuando se varía la tasa de crecimien-to de la demanda −0,04 y 0,04. Capacidad de generación en construcción.
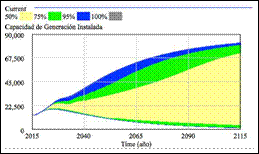
Figura 8: Análisis de sensibilidad numérica, cuando se varía la tasa de crecimiento de la demanda −0,04 y 0,04. Capacidad de generación instalada.
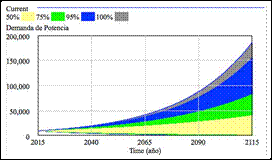
Figura 9: Análisis de sensibilidad numérica, cuando se varía la tasa de crecimiento de la demanda −0,04 y 0,04. Demanda de potencia.
En resumen, es posible utilizarlo en modelos que se puedan representar mediante sistemas de ecuaciones diferenciales ordinarias y que adicionalmente presentan no suavidades o saltos en sus expresiones funcionales. Se decidió utilizar esta herramienta debido a que gran parte de los sistemas modelados con dinámica de sistemas implican decisiones, y éstas, a su vez, involucran no suavidades. De esta manera, se pueden evidenciar los fenómenos asociados a las no suavidades y evaluar alternativas e información adicional que ofrecen los mapeos para explotar los modelos.
Para el modelo que se muestra en la Figura 4, la capacidad a construir es una función escalonada, que a su vez depende de una decisión de inversión igualmente no suave. De ahí que sea de gran interés evaluar qué sucede con las decisiones alrededor de la inversión y la capacidad a construir. En la Figura 10, se muestra cómo, para cada valor de b en el intervalo entre 0 y 48 ($/kWh), aparece un gran número de puntos. Esto significa que la capacidad a construir está variando sustancialmente si el precio mínimo de generación se encuentra en esos rangos (14). Se realizan las proyecciones sobre las variables de estado, o de nivel, para comprender cómo se comportarían frente a un valor del parámetro en específico. Mayor cantidad de puntos implica diferentes decisiones de inversión, lo que llevaría a los operadores a moverse entre inversión y desinversión. Con este tipo de herramienta se explora la sensibilidad frente a los modos de comportamiento, es decir, para valores alrededor de cero el sistema presenta oscilaciones, mientras que para valores por encima de 48 ($/kWh) la dinámica es monótona. Vale la pena mencionar que estos comportamientos se encuentran dentro de los posibles intervalos a los que se enfrentaría el mercado real.
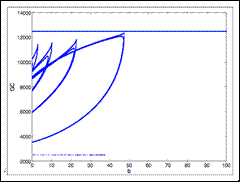
Figura 10: A-Switching map, en el que se mapea la capacidad de generación en construcción variando el precio mínimo (0 − 100$/kWh).
Finalmente, se dice que existe sensibilidad en las políticas, cuando un cambio en las hipótesis revierte los impactos o conveniencia de una política propuesta. Para ello, por ejemplo, en el caso del mercado nacional de electricidad, se propone variar el esquema bajo el cual se calcula el precio de generación del sistema, analizando dos escenarios posibles:
En el primer modelo de prueba, para el precio Pgen, el margen de reserva, MR, no podrá ser negativo, mientras que el parámetro b, que define el cargo por confiabilidad, es constante (ver Ecuación (3)). Ahora bien, explorando casos extremos, en el segundo modelo de prueba, el margen de reserva puede ser negativo, mientras que el cargo por confiabilidad dejó de ser constante (ver Ecuaciones (4) y (5)).
Al realizar el análisis de sensibilidad ante las políticas de los esquemas en el primer y segundo modelos de prueba, se aprecia cómo al variar el cargo por confiabilidad, el primer modelo de prueba, presenta mayor variabilidad que el segundo modelo de prueba (ver Figuras 11 y 12). Ello permite establecer una política más robusta asociada al precio de generación de acuerdo a lo establecido por las Ecuación (4) y (5).
Ahora bien, de un estudio más detallado, es posible encontrar la influencia de este parámetro en el comportamiento del mercado, de manera analítica. Por lo anterior se sugiere realizar un análisis cualitativo, de donde se concluyen asuntos como los siguientes: las decisiones de inversión y la capacidad a construir, al ser superficies de conmutación, dan lugar a planos de discontinuidad.
Si se logra establecer el rango para el cual el flujo dinámico del mercado evoluciona sin tener que conmutar entre las superficies, se reduce la variabilidad en las decisiones de los operadores. De manera adicional, si se comparan las Ecuación (3) y (4) con la Ecuación (2) que define el ROI, es más claro que los parámetros asociados a este último son los que afectan significativamente la distribución del retrato de fase. Dichos parámetros son los que definen los puntos de apalancamiento del sistema, junto a la la tasa de crecimiento de la demanda, que determina la estabilidad del mismo. Así, se pueden concentrar los esfuerzos de análisis de sensibilidad en ellos para aprovechar en mayor medida el modelo.
4 Discusión
Como se ha expuesto en la sección 1 de este documento, existe una amplia gama de estrategias para modelar, simular y formular elementos de política en mercados de electricidad. Si por el contrario, se exploran las ecuaciones diferenciales que surgen de los mismos, en menor medida aparecerán reportes en este sentido. Ahora bien, ¿cuál es la necesidad de este planteamiento?; de acuerdo a la síntesis metodológica que se propone seguir en este trabajo, se reconoce la pertinencia del análisis cualitativo de modelos basados en dinámica de sistemas. Para los científicos que están familiarizados con el tema, sabrán que formular un sistema de ecuaciones diferenciales que represente el comportamiento complejo de un sistema económico o social, no es tan sencillo como para los sistemas físicos reales. Quedan ciertamente en el aire algunas variables que pueden ser endogenizadas, o por el contrario, evaluar sus efectos de manera exógena para llegar a alguna conclusión. Pues bien, si se aprovecha la formulación basada en dinámica de sistemas, llegar a este tipo de representación y obtener un sistema de ecuaciones diferenciales es mucho más sencillo y sistemático.
Debido a la cantidad de decisiones que se deben tomar de manera no suave. Es posible que en el comportamiento cualitativo pueda darse lugar a bifurcaciones inducidas por discontinuidades. Como se ha demostrado en la Figura 5., se puede notar con claridad que debido a las diferentes decisiones de inversión del operador, el sistema presenta además de indefinidas oscilaciones, comportamientos tendenciales e incluso caos determinista. En este sentido, ya en algunos casos de estudio, se han encontrado dinámicas caóticas en modelos económicos basados en dinámica de sistemas. Vale la pena aclarar que son sistemas económicos debido a que la teoría del caos es ampliamente utilizada en los sistemas físicos reales para estudiar su comportamiento y en menor medida para sistemas sociales.
Ahora bien, en sistemas económicos basados en dinámica de sistemas los ejemplos son mas escasos, aunque Sterman desde 1989 ya reportaba comportamientos periódicos, puntos fijos y dinámicas caóticas en su documento titulado Deterministic chaos in an experimental economic system 16 y más recientemente en su libro de Business Dynamics 3. En estas publicaciones se refuerza el argumento de como las diferentes decisiones que se aplican en un modelo basado en dinámica de sistemas; desencadenan comportamientos aleatorios para modelos deterministas. En un trabajo aún mas reciente, es posible evidenciar fenómenos que implican desde ciclos limite, pasando por doblamientos de periodos en ruta hacia el caos para un modelo basado en dinámica de sistemas que describe una cadena de producción 20; de manera simple el autor expone un ejemplo representativo de como utilizando la teoría clásica de los sistemas dinámicos es posible encontrarse con estos fenómenos y, el modelo de partida esta basado en pensamiento sistémico. Es por este tipo de reportes encontrados en la literatura que surge la motivación de estudiar a profundidad los modelos basados en dinámica de sistemas y ampliar la explotación de dichos modelos utilizando herramientas adicionales que tradicionalmente no son muy utilizadas en el área de los mercados de electricidad basados en dinámica de sistemas.
En lo que respecta a la teoría del caos, ésta ha sido utilizada en mercados de electricidad para predecir precio de venta al consumidor y sus variaciones. Se esperaría que dicha teoría fuese ampliamente utilizada para determinar la dinámica de un mercado de electricidad debido a la cantidad de factores que lo afectan 21. En esencia es posible utilizar modelos deterministas que presenten un comportamiento aleatorio, en ese caso se podría predecir la aleatoriedad del precio de generación en el mercado de electricidad, por mencionar un ejemplo. Se ha encontrado que la teoría del caos ha sido utilizada para entender como los parámetros de entrada en modelos de series de tiempo presentan una dinámica caótica 21. Para este caso, han recurrido a la teoría clásica de sistemas dinámicos y calculando los exponentes de Lyapunov determinando si el precio de un mercado de electricidad era o no caótico 22.
Si se entienden los elementos de política energética como elementos de control para un marco regulatorio. Los operadores podrán entonces, basados en modelos de dinámica de sistemas, que con un análisis cualitativo arroja información adicional, decidir invertir en el cargo por confiabilidad en vez de aumentar el precio de escases, por ejemplo. Vale la pena utilizar además del análisis de sensibilidad que ofrecen los paquetes de simulación, análisis de sensibilidad que se estructuran cómo mapeos asíncronos, para este tipo de sistemas permite explorar lo que sucede en el estado transitorio.
5 Conclusiones
Se ha demostrado que mediante el uso de un conjunto de herramientas numéricas y cualitativas, utilizadas en este documento, se pueden estudiar los sistemas que modelan la oferta y la demanda de electricidad en un mercado nacional. Combinando dichas estrategias, se puede incluso clasificar y modelar fenómenos no suaves. Pretender realizar un estudio puramente analítico implica mayor complejidad en la búsqueda de soluciones e incluso no poder encontrar respuesta a los fenómenos de los que se hacen mención. Un propósito de este documento es constatar el valor agregado y la complementariedad entre la dinámica de sistemas y el análisis dinámico. Se concluye entonces que, en cuanto a aspectos metodológicos vale la pena reconciliar la parte matemática y la abstracción de esquemas mentales que ofrece la dinámica de sistemas. Es decir, se puede explotar la información que se logra traducir a ecuaciones diferenciales de manera más amplia, permitiendo reconocer variables en los puntos de apalancamiento del sistema, acercándose mediante una metodología sistemática a una mejor comprensión del problema.
Específicamente, se ha estudiado el modelo para un mercado de electricidad nacional, realizando a éste el análisis no lineal y de simulación. Se concluye que el análisis no lineal es una herramienta útil a la hora de caracterizar los diferentes fenómenos que este tipo de sistemas exhibe. Utilizar herramientas como los mapeos asíncronos resulta ciertamente novedoso en este campo y para este tipo de mercados. El esquema bajo el cual se realiza la integración numérica de soluciones es el adecuado. Otro resultado que resalta en este trabajo es cómo del análisis sistemático es posible identificar puntos de apalancamiento, como en el caso del retorno sobre la inversión expuesto. Ello abre nuevas preguntas de investigación acerca de cómo los parámetros juegan un rol significativo en los puntos de apalancamiento del sistema.
Se destaca desde el punto de vista metodológico, cómo el uso de mapeos asíncronos facilita en éste tipo de modelos realizar un análisis de sensibilidad y evidenciar para valores específicos de los parámetros modos de comportamiento. Para éste tipo de sistemas y mercados, no hay reportes en la literatura que relacionen métodos semejantes. En consonancia con la aplicación de métodos numéricos, también se logró evidenciar del análisis cualitativo, como por ejemplo el ROI y sus parámetros asociados, representan puntos de apalancamiento del sistema, debido a que los mismos varían las pendientes de las superficies de conmutación, cambiando con ello el comportamiento del mercado.
Así como se ha visto a lo largo del documento, comprender los estados transitorios de los modelos es ciertamente engorroso. Por lo mismo, y debido a la naturaleza del mercado y el modelo propuesto, el realizar un análisis cómo el que aquí se propone, garantiza un patrón de comportamiento para unos valores específicos de los parámetros. Por ello, no basta con presentar análisis numéricos que indiquen cuanto y cómo esta variando un comportamiento dado, también se debe decir bajo que circunstancias y para que valores. Éste tipo de planteamiento es la primera vez que se discute para un mercado de electricidad nacional basado en dinámica de sistemas. Además, si se entienden los elementos de política energética como elementos de control, los operadores podrán decidir invertir en el cargo por confiabilidad en ves de aumentar el precio de escasez, basados en modelos de dinámica de sistemas, que con un análisis cualitativo arrojan información adicional, por ejemplo. Vale la pena utilizar además del análisis de sensibilidad que ofrecen los paquetes de simulación, análisis de sensibilidad que se estructuran cómo mapeos asíncronos, dado que para este tipo de sistemas es mucho más interesante explorar lo que sucede en el estado transitorio que en el estado invariante.
Es de aclarar que, todo lo que implica la obtención del sistema de ecuaciones así como su análisis cualitativo ha sido presentado en 11, ya que el propósito de este artículo es reconocer la pertinencia y complementariedad entre la dinámica de sistemas y sistemas dinámicos para el estudio de mercados nacionales de electricidad.