1 Introducción
Los ensayos no-destructivos representan una alternativa rápida, económica y suficiente para estimar la resistencia a compresión uniaxial (σ ci ) del material rocoso y así poder evaluar su calidad. Entre los ensayos no-destructivos más utilizados se encuentran el ensayo de ultrasonido (ASTM E114) y el ensayo con martillo Schmidt (ASTM D5873). Aunque entre los dos, el en- sayo con martillo Schmidt es el más usado debido al bajo costo, tanto del ensayo como del equipo, su versatilidad y menor tiempo de ejecución. Con lo cual ha logrado obtener una gran aceptación y aplicación dentro de la comunidad ingenieril.
Muchos investigadores han desarrollado correlaciones entre el valor de rebote Schmidt (R) con la resistencia a la compresión uniaxial (σ ci ) del material rocoso, siendo algunos directamente aplicables a todo tipo de rocas, como [1-6] y otros de manera específica, como [7-12] para rocas sedimentarias; arenisca, limolita, caliza y anhidrita; mármol, limolita y dolomía; esquisto micáceo y verde; gabro y basalto; y rocas volcánicas respectivamente, entre otros. Del mismo modo, existen varios métodos para la ejecución del ensayo con martillo Schmidt, entre los cuales se puede nombrar a [13-17], entre otros.
Si bien en la actualidad existe una amplia gama de métodos, todos, a excepción del método propuesto por Suarez-Burgoa en [18], se limitan a medir ciertos puntos del espécimen de prueba de manera aleatoria y a través de criterios propios de cada método se obtiene la resistencia a com- presión uniaxial (σ ci ) de todo el espécimen. Este hecho, en concordancia con Suarez-Burgoa [18], puede dar lugar a falsas estimaciones de la resistencia mecánica, puesto que puede darse el caso en el cual el relevamiento se realice en los puntos más fuertes o débiles.
Por otro lado, la geoestadística, definida así por Georges Matheron en 1962, se caracteriza por proveer descripciones cuantitativas de variables naturales distribuidas en el espacio o en el tiempo y espacio. Su aplicación en un inicio ha estado centrada principalmente en las ciencias de la tierra, pero con el paso del tiempo su aplicación ha alcanzado diferentes campos de la ciencia, como ser la topografía, oceanografía, geofísica, agricultura, ciencias del suelo y medio-ambientales, entre otras.
Por consiguiente, Suarez-Burgoa [18] para mitigar las desventajas observadas en los métodos clásicos para la ejecución del ensayo con martillo Schmidt, propuso un método alternativo más sistemático empleando la geoestadística, como un primer intento para fusionar estas áreas del cono- cimiento. Con dicho fin, realizó una campaña de ensayos no-destructivos con el martillo de rebote Schmidt para rocas (tipo L) para estimar la variabilidad mecánica de una placa de sodalita (mármol sodalítico tipo Blue Sapo), de 0.05 m de espesor en un área cuadrada de 2 m de lado. La placa de sodalita fue escogida al azar de un lote de producción, con dimensiones mayores al área de análisis de 2 m de lado, como se puede apreciar en la Figura 1, y en su interior se dibujó una malla rectangular de 9 puntos por lado en ambas direcciones y espaciados a 0.2 m, obteniéndose así 81 puntos de ensayo dentro del área de la placa de sodalita. Finalmente, determinó la resistencia a compresión uniaxial (σ ci ) mediante la correlación empírica de Sachpazis [9] Ecuación (1), aunque aclara que dicha correlación es para mármoles se puede asemejar al tipo de roca en análisis.
Con este estudio, Suarez-Burgoa [18] pudo determinar la variabilidad mecánica al interior del área sugerida, con lo que pudo observar una variación elevada en la resistencia a compresión uniaxial (σ ci ), demostrando de esta manera que la resistencia obtenida es variable y no constante, como lo establecen los métodos clásicos. En consecuencia, su estudio surge como un método alternativo para estimar la variabilidad mecánica de placas de material rocoso y que pueda ser utilizado en procesos de control de calidad para revestimiento de pisos.
Dadas las ventajas de realizar un análisis variacional sobre la resistencia mecánica de placas de material rocoso, surge la necesidad de aplicar métodos de análisis geoestadísticos más rigurosos para poder validar el método propuesto por Suarez-Burgoa [18] y mejorar su aplicabilidad a toda la gama de placas de material rocoso que se disponen en el mercado para el revestimiento de pisos, obteniéndose así un método alternativo más sólido. Es con este propósito, que el presente estudio expone un análisis complementario basado en la geoestadística. Por lo tanto, se hizo un análisis exploratorio más detallado, tomando en cuenta la resistencia a compresión uniaxial (σ ci ), para poder analizar la existencia o no de tendencia en los datos y su distribución a través de un histograma de frecuencia; análisis de anisotro- pía a 0◦, 30◦, 60◦, 90◦, 120◦y 150◦, tomando como referencia el eje positivo “Y” y positivo en sentido horario; verificación del modelo geoestadístico a través de la comparación de modelos alternativos obtenidos a partir del método de mínimos cuadrados ordinarios, mínimos cuadrados ponderados y máxima verosimilitud para determinar el modelo más óptimo a través de una validación cruzada; verificación de la estructura espacial a través de la envolvente de permutaciones y bajo un modelo específico para validar la dependencia espacial; verificación del tamaño de muestra propuesto por Suarez-Burgoa [18] a través de la simulación del campo aleatorio para validar la malla de relevamiento de datos; modelación de la distribución espacial de la resistencia mecánica a través de un modelo de señal para la predicción de valores por el método de krigeado simple.
En este estudio complementario se utilizó el software libre R®v3.4.1 y los paquetes ggplot2, geoR y RandomFields para el análisis, simulación y modelación de la distribución espacial de la resistencia mecánica de la placa de roca.
2 Análisis geoestadístico
El análisis de la distribución espacial de la resistencia mecánica de la placa de roca se basó en un modelo geoestadístico de señal [19] y [20], descrito por la Ecuación (2).
Donde Z(s) representa la variable aleatoria en la ubicación s, S(s) representa el proceso de señal y e(s) representa la medición del error.
2.1 Análisis exploratorio
El análisis exploratorio se realizó con la finalidad de analizar la existencia o no de tendencia en los datos, tomando en cuenta la resistencia a compresión uniaxial Ecuación (1), y también determinar algunos parámetros estadísticos, como la media (µ) y la varianza (σ2).
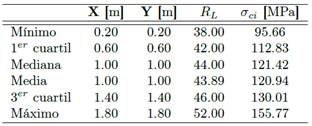
En la Tabla 1 se resume el relevamiento de datos del ensayo con martillo Schmidt tipo L en la placa de sodalita. Los datos de muestreo tienen una media, µ = 120.94, y una varianza, σ2 = 188.07.
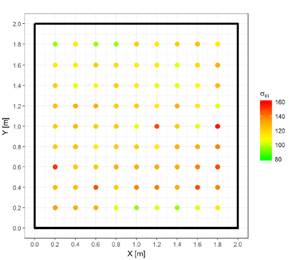
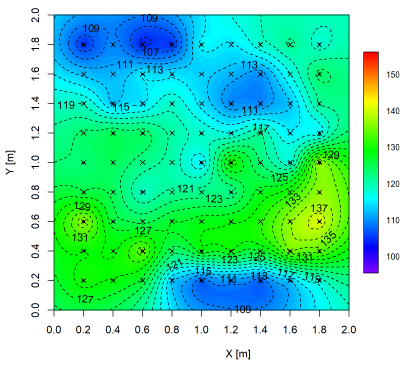
Del mismo modo, en la Figura 2 se emplaza la malla de relevemiento de datos y la respuesta medida en la placa de sodalita.
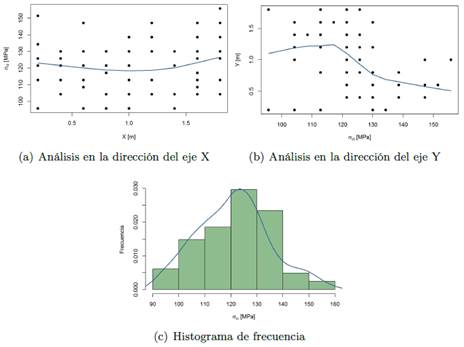
Para determinar preliminarmente la existencia o no de tendencia en los datos de muestreo, se ha realizado un análisis en la dirección de los ejes “X” y “Y”, Figura 3(a) y Figura 3(b) respectivamente. Estas gráficas muestran la relación de la respuesta obtenida con los ejes analizados, con lo que se puede intuir alguna tendencia (línea azul) a lo largo de dichos ejes. Por lo tanto, se puede observar en la Figura 3(a) una mínima tendencia a lo largo del eje “X”, a diferencia de lo observado en la Figura 3(b) donde existe una tendencia poco más notoria, pero aún pequeña. Este hecho también puede ser observado a través del histograma de frecuencia, Figura 3(c), puesto que se aproxima a una distribución normal.
2.2 Análisis de anisotropía
El análisis de anisotropía se realizó con la finalidad de determinar direcciones preferenciales de continuidad en el espacio de la variable regionalizada. Por tanto, su estimación depende principalmente de la dirección de los semivariogramas, ya que está en función de la correlación entre los datos.
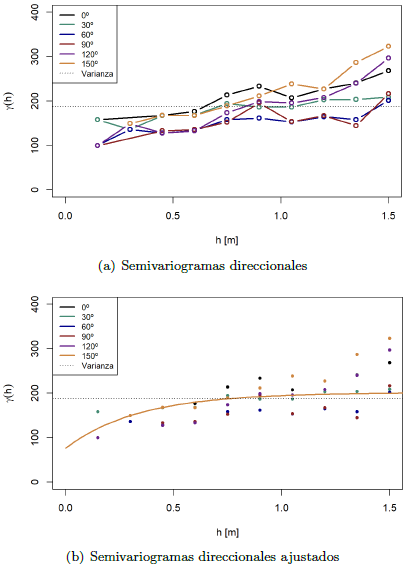
Las direcciones de los semivariogramas fueron fijadas a 0◦, 30◦, 60◦, 90◦, 120◦ y 150◦, tomando como referencia el eje positivo “Y” y positivo en sentido horario [21--23]. Asimismo, se asumió un modelo Matérn para ajustar cada semivariograma direccional por el método de máxima verosimilitud [Figura 4].
En la Figura 4(a) se puede observar que los semivariogramas direccionales se encuentran muy próximos entre sí, con lo que se puede intuir una posible isotropía del modelo geoestadístico.
En la Figura 4(b) y Tabla 2 se puede observar que los semivariogramas direccionales ajustados se sobreponen, por lo tanto, el modelo geoestadístico puede considerarse isótropo. Cabe resaltar que este resultado es opuesto al obtenido por Suarez-Burgoa [18].
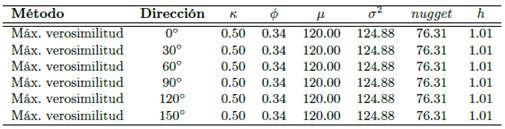
En la Tabla 2 se detallan los parámetros de los semivariogramas direccionales ajustados a modelos Matérn por máxima verosimilitud, siendo κ, φ y nugget coeficientes de forma, µ la media, σ2 la meseta y h el rango práctico.
Para casos de estudio donde el modelo geoestadístico sea anisótropo se recomienda reportar los semivariogramas direccionales ajustados en un gráfico de rosa de los vientos. Esto con el objetivo de identificar de forma más clara las direcciones preferenciales.
2.3 Verificación del modelo asumido
Para verificar si el modelo Matérn por máxima verosimilitud asumido es el más óptimo, se hizo una comparación entre modelos a partir del método de mínimos cuadrados ordinarios, mínimos cuadrados ponderados y máxima verosimilitud por medio de una validación cruzada.
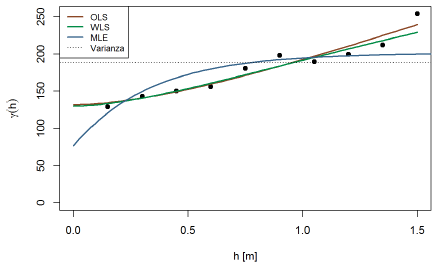
La Tabla 3 y Figura 5 exponen los modelos Matérn obtenidos por los métodos en análisis, tanto en forma paramétrica como visual.
En la Tabla 3 los parámetros κ, φ y nugget son coeficientes de forma, µ la media, σ2 la meseta y h el rango práctico.
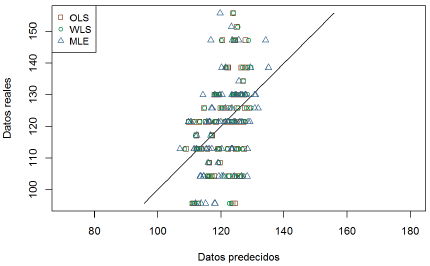
En la Figura 6 y Tabla 4 se puede observar que el modelo Matérn más óptimo es aquel obtenido por el método de máxima verosimilitud ya que presenta la menor desviación estándar de errores (σ std.error ) entre los tres métodos considerados. Por lo tanto, el modelo asumido queda verificado.
Cabe resaltar, que los tres métodos analizados son potencialmente elegibles dada la pequeña diferencia en la desviación estándar de errores (σ std.error ) entre ellos, sin embargo se decidió optar por el método de máxima verosimilitud porque la meseta (σ2) se aproxima mejor a la varianza de los datos muestreados (línea punteada) y numéricamente tiene el mejor ajuste.
2.4 Verificación de la estructura espacial
Para verificar la existencia de estructura espacial, se ha realizado un análisis a través de la envolvente de permutaciones y la envolvente bajo el modelo por máxima verosimilitud [21].
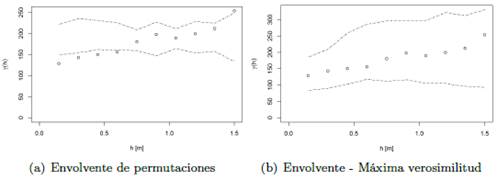
En la Figura 7(a) se puede observar que la primera parte del semivariograma se encuentra fuera de la envolvente y en la Figura 7(b) todo el semivariograma se encuentra dentro de la envolvente. Con lo que se verifica que existe dependencia espacial.
Cabe destacar, que la diferencia en los rangos de las envolventes de la Figura 7 se debe a que la envolvente de permutaciones está construida bajo la asunción de que no existe correlación espacial mientras que la envolvente por máxima verosimilitud está construida a partir de los parámetros del modelo teórico mostrando la variabilidad del semivariograma empírico. Por lo tanto, se recomienda la aplicación de estos dos criterios para la evaluación de la dependencia espacial.
2.5 Verificación del tamaño de muestra
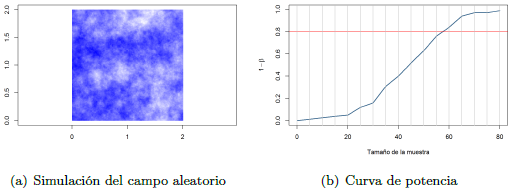
Para verificar el tamaño de muestra propuesto por Suarez-Burgoa [18] para el relevamiento de datos, se realizó una simulación del campo aleatorio del modelo geoestadístico asumido entre 10 y 80 puntos de la malla propuesta, con el cual se obtuvo la curva de potencia y se determinó el tamaño de muestra mínimo [Figura 8].
En la Figura 8(b) se puede observar que el tamaño de muestra mínimo es de 60 puntos aproximadamente. Por lo tanto, se valida la malla propuesta por Suarez-Burgoa [18] para el relevamiento de datos con el martillo Schmidt-L, puesto que se relevaron 81 puntos.
2.6 Mapa de la distribución espacial de la resistencia mecánica
Para la construcción del mapa de la distribución espacial de la resistencia mecánica de la placa de sodalita, se consideró el método de krigeado simple tomando en cuenta el modelo de señal Ecuación (2).
3 Conclusiones
Con este estudio se confirma que la variabilidad mecánica de la placa de sodalita es elevada, puesto que se encuentra en un rango entre 95.66 MPa y 155.77 MPa. Este hecho es un indicador contrastante respecto de los méto- dos clásicos, ya que indican que el muestreo debe realizarse alrededor de un punto aleatorio y en ciertos sectores de la placa de roca, asumiendo de esta manera una resistencia global y generando la incertidumbre de que la medición se haya realizado en zonas débiles o fuertes, con lo que se obtendrían falsas estimaciones de su resistencia.
También, se comprueba que la placa de sodalita cumple los requisitos de resistencia para disponerla como revestimiento de piso, puesto que la re- sistencia mínima obtenida fue de 95.66 MPa. Por lo tanto, se puede aprobar el lote de producción de la misma.
Con todos los pasos descritos en este estudio, basados principalmente en la geoestadística, se puede extrapolar este método alternativo, propuesto por Suarez-Burgoa [18], a toda la gama de placas de material rocoso disponibles en el mercado para el revestimiento de pisos.
Este método alternativo sólo puede ser aplicado a placas de material rocoso destinados al revestimiento de pisos, debido a que las solicitaciones para otros usos, como mesones, requieren un estudio complementario para determinar su resistencia a corte y flexión.
Finalmente, se recomienda determinar si existe algún grado de fisuramiento y su efecto en la resistencia, que se haya podido suscitar en el relevamiento de datos por medio del martillo Schmidt-L.
Asimismo, realizar un estudio comparativo considerando correlaciones más actualizadas que se adecúen al tipo de roca en análisis para mejorar la estimación de la variabilidad de la resistencia mecánica de la placa de sodalita.