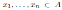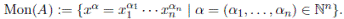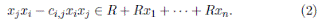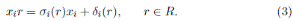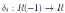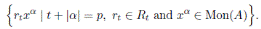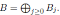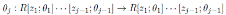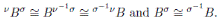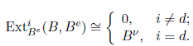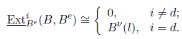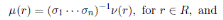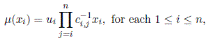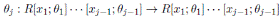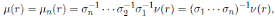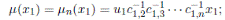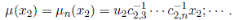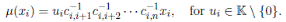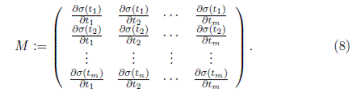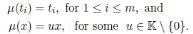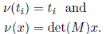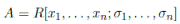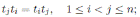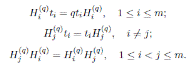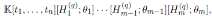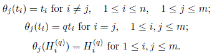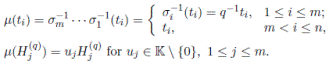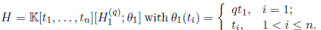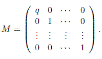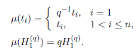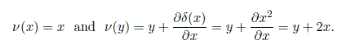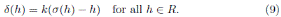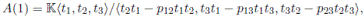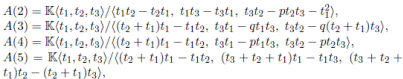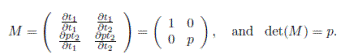1 Introduction
There are two notions of Nakayama automorphisms: one for skew Calabi-Yau algebras and another for Frobenius algebras. In this paper, we focus on skew Calabi-Yau algebras, or equivalently, Artin-Schelter regular algebras in the connected graded case (Proposition 2.7). The Nakayama automorphism is one of important homological invariants for Artin-Schelter regular algebras algebras. Nakayama automorphisms have been studied by several authors. Reyes, Rogalski and Zhang in [1] proved three homological identities about the Nakayama automorphism and gave several applications. Liu, Wang and Wu in [2] proved that if R is skew Calabi-Yau with Nakayama automorphism ν then the Ore extension
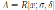 has Nakayama automorphism ν
j such that
has Nakayama automorphism ν
j such that
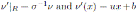 with
with
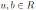 and u invertible, the parameters u and b are still unknown. Zhu, Van Oystaeyen and Zhang computed the Nakayama automorphisms of trimmed double Ore extensions and skew polynomial extension
and u invertible, the parameters u and b are still unknown. Zhu, Van Oystaeyen and Zhang computed the Nakayama automorphisms of trimmed double Ore extensions and skew polynomial extension
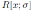 , where σ is a graded algebra automorphism of R in terms of the homological determinant. Lü, Mao and Zhang in [3] and [4] used the Nakayama automorphism to study group actions and Hopf algebra actions on Artin-Schelter regular algebras of global dimension three and calculated explicitly the Nakayama automorphism of a class of connected graded Artin-Schelter regular algebras. Shen, Zhou and Lu in [5] described the Nakayama automorphisms of twisted tensor products of noetherian Artin-Schelter regular algebras. Liu and Ma in [6] gave an explicit formula to calculate the Nakayama automorphism of any Ore extension
, where σ is a graded algebra automorphism of R in terms of the homological determinant. Lü, Mao and Zhang in [3] and [4] used the Nakayama automorphism to study group actions and Hopf algebra actions on Artin-Schelter regular algebras of global dimension three and calculated explicitly the Nakayama automorphism of a class of connected graded Artin-Schelter regular algebras. Shen, Zhou and Lu in [5] described the Nakayama automorphisms of twisted tensor products of noetherian Artin-Schelter regular algebras. Liu and Ma in [6] gave an explicit formula to calculate the Nakayama automorphism of any Ore extension
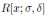 over a polynomial algebra
over a polynomial algebra
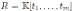 for an arbitrary m. In general, Nakayama automorphisms are known to be tough to compute.
for an arbitrary m. In general, Nakayama automorphisms are known to be tough to compute.
Skew PBW extensions and quasi-commutative skew PBW extensions were defined in [7] and are non-commutative rings of polynomial type defined by a ring and a set of variables with relations between them. Skew PBW extensions include rings and algebras coming from mathematical physics such PBW extensions, group rings of polycyclic-by-finite groups, Ore algebras, operator algebras, diffusion algebras, some quantum algebras, quadratic algebras in three variables, some 3-dimensional skew polynomial algebras, some quantum groups, some types of Auslander-Gorenstein rings, some Koszul algebras, some Calabi-Yau algebras, some Artin-Schelter regular algebras, some quantum universal enveloping algebras, and others. There are some special subclasses of skew PBW extensions such as bijective, quasi-commutative, of derivation type and of endomorphism type (see Definition 2.2). Some noncommutative rings are skew PBW extensions but not Ore extensions (see [8],[9] and [10]).
Several properties of skew PBW extensions have been studied in the literature (see for example [11],[12],[13],[14],[15],[16]). It is known that quasi-commutative skew PBW extensions are isomorphic to iterated Ore extensions of endomorphism type (see (8, Theorem 2.3)). In [9] it was defined graded skew PBW extensions with the aim of studying Koszul property in these extensions.
The Nakayama automorphism has not been studied explicitly for skew PBW extensions. In this paper we focus on the Nakayama automorphism of quasi-commutative skew PBW extensions (Section 3) and non quasicommutative skew PBW extensions of the form
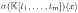 (Section 4). Since every graded quasi-commutative skew PBW extension is isomorphic to a graded iterated Ore extension of endomorphism type (see (17, Proposition 2.7)), we have that if A is a graded quasi-commutative skew PBW extension of an Artin-Schelter regular algebra R, then A is Artin-Schelter regular (see Proposition 3.1). Now, for B a connected graded algebra, B is Artin-Schelter regular if and only if B is graded skew Calabi-Yau (see [1]), and hence the Nakayama automorphism of Artin-Schelter regular algebras exists. Therefore, if R is an Artin-Schelter regular algebra with Nakayama automorphism ν, then the Nakayama automorphism µ of a graded quasi-commutative skew PBW extension A exists, and we compute it using the Nakayama automorphism ν together some especial automorphisms of R and A (see Theorem 3.1). The main results in Section 3 are Theorem 3.1, Corollary 3.2, Proposition 3.3, Corollary 3.3 and Examples 3.1, 3.2. Since Ore extensions of bijective type are skew PBW extensions. In Section 4 we use the results of [6] to calculate explicitly the Nakayama automorphism of some skew PBW extensions (Examples 4.1, 4.2 and Proposition 4.1).
(Section 4). Since every graded quasi-commutative skew PBW extension is isomorphic to a graded iterated Ore extension of endomorphism type (see (17, Proposition 2.7)), we have that if A is a graded quasi-commutative skew PBW extension of an Artin-Schelter regular algebra R, then A is Artin-Schelter regular (see Proposition 3.1). Now, for B a connected graded algebra, B is Artin-Schelter regular if and only if B is graded skew Calabi-Yau (see [1]), and hence the Nakayama automorphism of Artin-Schelter regular algebras exists. Therefore, if R is an Artin-Schelter regular algebra with Nakayama automorphism ν, then the Nakayama automorphism µ of a graded quasi-commutative skew PBW extension A exists, and we compute it using the Nakayama automorphism ν together some especial automorphisms of R and A (see Theorem 3.1). The main results in Section 3 are Theorem 3.1, Corollary 3.2, Proposition 3.3, Corollary 3.3 and Examples 3.1, 3.2. Since Ore extensions of bijective type are skew PBW extensions. In Section 4 we use the results of [6] to calculate explicitly the Nakayama automorphism of some skew PBW extensions (Examples 4.1, 4.2 and Proposition 4.1).
We establish the following notation: the symbol N is used to denote the set of natural numbers including zero. If α: = (α 1 , . . . , α n ) ∈ Nn then |α| := α 1 + · · · + α n . The letter K denotes a field. Every algebra is a K-algebra.
2 Preliminaries
In this section, we fix basic notations and recall definitions and properties for this paper.
Definition 2.1. Let R and A be rings. We say that A is a skew PBW extension over R, if the following conditions hold:
(i) R ⊆ A;
(ii) there exist elements
such that A is a left free R-module, with basis the basic elements
In this case, it is said also that A is a left polynomial ring over R with respect to {x 1 , · · · , x n } and Mon(A) is the set of standard monomials of A. Moreover, x 1 0 · · · x n 0: = 1 ∈ Mon(A).
Under these conditions, we will write
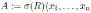 .
.
The notation
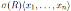 and the name of the skew PBW extensions are due to the next proposition.
and the name of the skew PBW extensions are due to the next proposition.
Proposition 2.1 ([7], Proposition 3). Let A be a skew PBW extension of R. For each 1 ≤ i ≤ n, there exist an injective endomorphism σ i : R → R and a σ i -derivation δ i : R → R such that
In the following definition we recall some sub-classes of skew PBW extensions. Examples of these sub-classes of algebras can be found in [15].
Definition 2.2. Let A be a skew PBW extension of R, Σ := {σ 1 , . . . , σ n } and ∆ := {δ 1 , . . . , δ n }, where σ i and δ i (1 ≤ i ≤ n) are as in Proposition 2.1
A is called quasi-commutative, if the conditions (iii) and (iv) in Definition 2.1 are replaced by
for each 1 ≤ i ≤ n and all r ∈ R \ {0}, there exists c i,r ∈ R \ {0} such that
A is called bijective, if σ i is bijective for each σ i ∈ Σ, and c i,j is invertible for any 1 ≤ i < j ≤ n.
If σ i = id R for every σ i ∈ Σ, we say that A is a skew PBW extension of derivation type.
If δ i = 0 for every δ i ∈ ∆, we say that A is a skew PBW extension of endomorphism type.
The next proposition was proved in [9].
Proposition 2.2. Let
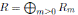 be a N-graded algebra and let A =
be a N-graded algebra and let A =
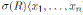 be a bijective skew PBW extension of R satisfying the following two conditions:
be a bijective skew PBW extension of R satisfying the following two conditions:
σ i is a graded ring homomorphism and
is a graded σ i -derivation for all 1≤ i ≤ n, where σ i and δ i are as in Proposition 2.1.x j x i − c i,j x i x j ∈ R 2 + R 1 x 1 + · · · + R 1 x n , as in (2) and c i,j ∈ R 0. For p ≥ 0, let A p the K-space generated by the set
Then A is a N-graded algebra with graduation
Definition 2.3 ( [9], Definition 2.6). Let
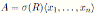 be a bijective skew PBW extension of a N -graded algebra
be a bijective skew PBW extension of a N -graded algebra
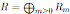 . We say that A is a graded skew PBW extension if A satisfies the conditions (i) and (ii) in Proposition 2.2.
. We say that A is a graded skew PBW extension if A satisfies the conditions (i) and (ii) in Proposition 2.2.
Note that the family of graded iterated Ore extensions is strictly contained in the family of graded skew PBW extensions (see (9, Remark 2.11)). Examples of graded skew PBW extensions can be found in [9] and [10].
Proposition 2.3. Quasi-commutative skew PBW extensions with the trivial graduation of R are graded skew PBW extensions. If we assume that R has a different graduation to the trivial graduation, then A is graded skew PBW extension if and only if σ i is graded and c i,j ∈ R 0, for 1 ≤ i, j ≤ n.
Proof. Let R = R 0 and r ∈ R = R 0. From (4) we have that x i r = c i,r x i = σ i (r)x i . So, σ i (r) = c i,r ∈ R = R 0 and δ i = 0, for 1≤ i ≤ n. Therefore σ i is a graded ring homomorphism and δ i : R( 1)→R is a graded σ i -derivation for all 1≤ i ≤ n. From (5) we have that x j x i - c i,j x i x j = 0 ∈ R 2 +R 1 x 1+· · · +R 1 x n and c i,j ∈ R = R 0. If R has a nontrivial graduation, then the result is obtained from the relations (4), (5) and Definition 2.3.
Let
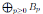 be an N-graded algebra. B is connected if B
0 = K. In (18, Definition 1.4) finitely graded algebra was presented. B is finitely graded if the following conditions hold:
be an N-graded algebra. B is connected if B
0 = K. In (18, Definition 1.4) finitely graded algebra was presented. B is finitely graded if the following conditions hold:
B is N-graded (positively graded):
B is connected.
B is finitely generated as algebra, i.e., there is a finite set of elements x 1 , . . . , x n ∈ B such that the set {x i 1 x i 2 · · · x i m | 1 ≤ i j ≤ n, m ≥ 1} ∪ {1} spans B as a vector space.
Note that a finitely graded algebra B is finitely generated as K-algebra if and only if
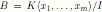 , where I is a proper homogeneous two-sided ideal of
, where I is a proper homogeneous two-sided ideal of
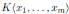 . A finitely graded algebra B is finitely presented if the two-sided ideal I is finitely generated.
. A finitely graded algebra B is finitely presented if the two-sided ideal I is finitely generated.
The following properties of graded skew PBW extensions were proved in [9].
Remark 2.1 ([9], Remark 2.10). Let
 be a graded skew PBW extension. Then we have the following properties:
be a graded skew PBW extension. Then we have the following properties:
A is a N-graded algebra and A 0 = R 0.
R is connected if and only if A is connected.
If R is finitely generated then A is finitely generated.
For (i), (ii) and (iii) above, we have that if R is a finitely graded algebra then A is a finitely graded algebra.
If R is locally finite, then A as K-algebra is a locally finite.
A as R-module is locally finite.
If R is finitely presented then A is finitely presented.
The following proposition establishes the relation between graded skew PBW extensions and graded iterated Ore extensions.
Proposition 2.4 ([17], Proposition 2.7). Let
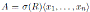 be a graded skew PBW extension. If A is quasi-commutative, then A is isomorphic to a graded iterated Ore extension of endomorphism type
be a graded skew PBW extension. If A is quasi-commutative, then A is isomorphic to a graded iterated Ore extension of endomorphism type
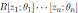 , where θ
i
is bijective, for each i; θ
1 = σ
1;
, where θ
i
is bijective, for each i; θ
1 = σ
1;
is such that θ j (z i ) = c i,j z i (c i,j ∈ R 0 as in (2)), 1 ≤ i < j ≤ n and θ i (r) = σ i (r), for r ∈ R.
If M and N are graded B-modules, we use
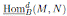 to denote the set of all B-module homomorphisms h: M → N such that
to denote the set of all B-module homomorphisms h: M → N such that 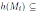
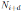 . We set
. We set
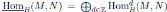 , and we denote the corresponding derived functors by
, and we denote the corresponding derived functors by
 .
.
Definition 2.4. Let B = K ⊕ B1 ⊕ B2 ⊕ · · · be a finitely presented graded algebra over K. The algebra B will be called Artin-Schelter regular, if B has the following properties:
B has finite global dimension d: every graded B−module has projective dimension ≤ d.
B has finite Gelfand-Kirillov dimension.
B is Gorenstein, meaning that ExtiB (K, B) = 0 if i ƒ= d, and ExtdB (K, B) ∼= K(l) for some l ∈ Z.
The enveloping algebra of a ring B is defined as
 . We characterize the enveloping algebra of a skew PBW extension in [12]. If M is an B-bimodule, then M is an Be module with the action given by
. We characterize the enveloping algebra of a skew PBW extension in [12]. If M is an B-bimodule, then M is an Be module with the action given by
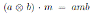 , for all m ∈ M , a, b ∈ B. Given automorphisms ν, τ ∈ Aut(B), we can define the twisted Be-module ν Mτ with the rule
, for all m ∈ M , a, b ∈ B. Given automorphisms ν, τ ∈ Aut(B), we can define the twisted Be-module ν Mτ with the rule
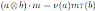 , for all m ∈ M , a, b ∈ B. When one or the other of ν, τ is the identity map, we shall simply omit it, writing for example Mν for 1Mν .
, for all m ∈ M , a, b ∈ B. When one or the other of ν, τ is the identity map, we shall simply omit it, writing for example Mν for 1Mν .
Proposition 2.5 ([19], Lemma 2.1). Let ν, σ and φ be automorphisms of B. Then
An algebra B is said to be homologically smooth, if as a Be-module, B has a finitely generated projective resolution of finite length.
Definition 2.5. An algebra B is called skew Calabi-Yau of dimension d if
as Be -modules. If ν is the identity, then B is said to be Calabi-Yau.
A graded algebra B is called graded skew Calabi-Yau of dimension d, if
as Be-graded modules, for some integer l. If ν is the identity, then Bis said to be graded Calabi-Yau.
The automorphism ν is called the Nakayama automorphism of B. As a consequence of Proposition 2.5, we have that a skew Calabi-Yau algebra is Calabi-Yau if and only if its Nakayama automorphism is inner. If B is a Calabi-Yau algebra of dimension d, then the Hochschild dimension of B (that is, the projective dimension of A as an A-bimodule) is d (see (20, Proposition 2.2)).
Proposition 2.6. Let B be a skew Calabi-Yau algebra with Nakayama automorphism ν. Then ν is unique up to an inner automorphism, i.e, the Nakayama automorphism is determined up to multiplication by an inner automorphism of B.
Proof. Let B be a skew Calabi-Yau algebra with Nakayama automorphism ν and let µ be another Nakayama automorphism, i.e., Extd Be (B, Be) ∼= Bµ, then Extd Be (B, Be) ∼= Bν ∼= Bµ as Be -modules. By Proposition 2.5-(i), B ∼= Bν−1µ; by Proposition 2.5-(ii), ν−1µ is an inner automorphism of B. Let ν−1µ = σ where σ is an inner automorphism of B, so µ = νσ for some inner automorphism σ of B.
Reyes, Rogalski and Zhang in [1], proved that Artin-Schelter regular algebras and graded skew Calabi-Yau algebras coincide for the connected case.
Proposition 2.7 ([1], Lemma 1.2). Let B be a connected graded algebra. Then B is graded skew Calabi-Yau if and only if it is Artin-Schelter regular.
3 Nakayama automorphism of quasi-commutative skew PBW extensions
Since graded quasi-commutative skew PBW extensions are isomorphic to graded iterated Ore extensions of endomorphism type, it follows that graded quasi-commutative skew PBW extensions with coefficients in Artin-Schelter regular algebras are skew Calabi-Yau, and the Nakayama automorphism exists for these extensions. With this in mind, in this section we give a description of Nakayama automorphism for these non-commutative algebras using the Nakayama automorphism of the ring of the coefficients.
The following properties of graded quasi-commutative skew PBW extensions were proved in (17, Theorem 3.6 and Theorem 4.5).
Proposition 3.1. Let
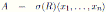 be a graded quasicommutative skew PBW extension of R.
be a graded quasicommutative skew PBW extension of R.
If R is Artin-Schelter regular, then A is Artin-Schelter regular.
If R is a finitely presented graded skew Calabi-Yau algebra of global dimension d, then A is graded skew Calabi-Yau of global dimension d + n.
As a consequence of Proposition 2.7 and Proposition 3.1 we have the following property.
Corollary 3.1. Let R be an Artin-Schelter regular algebra of global dimension d. Then every graded quasi-commutative skew PBW extension
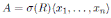 is graded skew Calabi-Yau of global dimension d + n.
is graded skew Calabi-Yau of global dimension d + n.
Liu, Wang and Wu in (2, Theorem 3.3) proved that if R is a skew Calabi-Yau algebra with Nakayama automorphism ν then the Ore extension
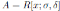 has Nakayama automorphism νj such that
has Nakayama automorphism νj such that
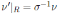 and νj(x) = ux + b with u, b ∈ R and u invertible. If δ = 0 then they deduced the following result.
and νj(x) = ux + b with u, b ∈ R and u invertible. If δ = 0 then they deduced the following result.
Proposition 3.2 ([2], Remark 3.4). With the above notation νj(x) = ux if δ = 0.
In the next theorem we show a way to calculate the Nakayama automorphism for a graded quasi-commutative skew PBW extension A of an Artin-Schelter regular algebra R.
Theorem 3.1. Let R be an Artin-Schelter regular algebra with Nakayama automorphism ν. Then the Nakayama automorphism µ of a graded quasicommutative skew PBW extension
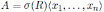 is given by
is given by
where σi is as in Proposition 2.1,
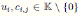 , and the elements ci,j are as in Definition 2.1.
, and the elements ci,j are as in Definition 2.1.
Proof. Note that A is graded skew Calabi-Yau (see Corollary 3.1) and therefore the Nakayama automorphism of A exists. By Proposition 2.4 we have that A is isomorphic to a graded iterated Ore extension
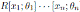 , where θi is bijective; θ1 = σ1;
, where θi is bijective; θ1 = σ1;
is such that θj(xi) = ci,jxi (ci,j ∈ K as in Definition 2.1), 1 ≤ i < j ≤ n and θi(r) = σi(r), for r ∈ R. Note that
Now, since R is connected then by Remark 2.1, A is connected. So, the multiplicative group of R and also the multiplicative group of A is K \{0}, therefore the identity map is the only inner automorphism of A. Let µi the Nakayama automorphism of
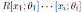 .
.
By Proposition 3.2 we have that the Nakayama automorphism µ1 of
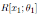 is given by
is given by
 for r ∈ R, and
for r ∈ R, and
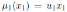 with u1 ∈ K \ {0}; the Nakayama automorphism µ2 of
with u1 ∈ K \ {0}; the Nakayama automorphism µ2 of
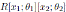 is given by
is given by
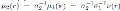 , for
, for
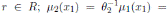
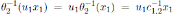 and
and
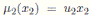 , for u2 ∈ K \{0}; the Nakayama automorphism µ3 of
, for u2 ∈ K \{0}; the Nakayama automorphism µ3 of
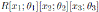 is given by
is given by
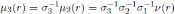 , for r ∈ R;
, for r ∈ R;
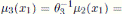
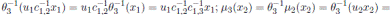
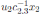 and
and
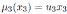 , for u3 ∈ K \{0}.
, for u3 ∈ K \{0}.
Continuing with the procedure we have that the Nakayama automorphismof A is given by
for r ∈ R, and
In general, for 1 ≤ i ≤ n, we have that
Note that ci,i = 1.
From Theorem 3.1 the following corollary is immediately obtained.
Corollary 3.2. Let
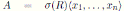 be a graded quasicommutative skew PBW extension of an Artin-Schelter regular algebra R with Nakayama automorphism ν. Then A is graded Calabi-Yau if and
be a graded quasicommutative skew PBW extension of an Artin-Schelter regular algebra R with Nakayama automorphism ν. Then A is graded Calabi-Yau if and
only if σ1 · · · σn = ν and
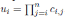 , for all 1 ≤ i ≤ n, where ui is as in Theorem 3.1.
, for all 1 ≤ i ≤ n, where ui is as in Theorem 3.1.
Let
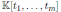 be the polynomial algebra and
be the polynomial algebra and
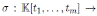
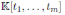 an algebra automorphism. We define
an algebra automorphism. We define
Remark 3.1. Liu and Ma proved in [6] that if
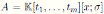 is an Ore extension then the Nakayama automorphism ν of A is given by ν(t
i
) = t
i
and ν(x) = det(M )x, where det(M ) is the usual determinant of the matrix M in (8). Note that
is an Ore extension then the Nakayama automorphism ν of A is given by ν(t
i
) = t
i
and ν(x) = det(M )x, where det(M ) is the usual determinant of the matrix M in (8). Note that
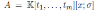 is a quasicommutative skew PBW extension and if σ is a graded automorphism then A is a graded quasi-commutative skew PBW extension.
is a quasicommutative skew PBW extension and if σ is a graded automorphism then A is a graded quasi-commutative skew PBW extension.
Let h ∈ K \ {0}. The algebra of shift operators is defined by S
h
: =
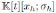 , where
, where
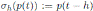 . Notice that
. Notice that
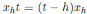 and for
and for
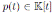 we have
we have
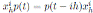 . Thus,
. Thus,
 is a quasi-commutative skew PBW extension of
is a quasi-commutative skew PBW extension of
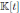 .
.
Proposition 3.3. The algebra of shift operators is a Calabi-Yau algebra.
Proof. Since
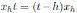 , then
, then
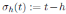 , then det
, then det
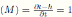 . By Remark 3.1 we have that the Nakayama automorphism ν of S
h
is given by ν(t) = t and ν(x
h
) = det(M )x = 1, i.e., the Nakayama automorphism of S
h
is the identity map. Therefore S
h
is Calabi-Yau.
. By Remark 3.1 we have that the Nakayama automorphism ν of S
h
is given by ν(t) = t and ν(x
h
) = det(M )x = 1, i.e., the Nakayama automorphism of S
h
is the identity map. Therefore S
h
is Calabi-Yau.
Corollary 3.3. Let
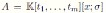 with σ be a graded algebra automorphism. Then u = det(M ), where u is as in Theorem 3.1 and M is as in (8).
with σ be a graded algebra automorphism. Then u = det(M ), where u is as in Theorem 3.1 and M is as in (8).
Proof. Note that
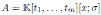 is a quasi-commutative skew PBW extension of the graded Calabi-Yau algebra
is a quasi-commutative skew PBW extension of the graded Calabi-Yau algebra
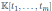 . Since σ is graded then A is a graded quasi-commutative skew PBW extension. By Theorem 3.1 we have that the Nakayama automorphism µ of A is given by
. Since σ is graded then A is a graded quasi-commutative skew PBW extension. By Theorem 3.1 we have that the Nakayama automorphism µ of A is given by
By Remark 3.1 we have that the Nakayama automorphism of A is given by
Since
 is connected, then by Remark 2.1 A is connected, so the multiplicative group of A is
is connected, then by Remark 2.1 A is connected, so the multiplicative group of A is
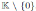 . Therefore the identity map is the only inner automorphism of A. As by Proposition 2.6 we have that the Nakayama automorphism is unique up to inner automorphisms, then ν must be equal to µ. So u = det(M ).
. Therefore the identity map is the only inner automorphism of A. As by Proposition 2.6 we have that the Nakayama automorphism is unique up to inner automorphisms, then ν must be equal to µ. So u = det(M ).
Example 3.1. Let R be an Artin-Schelter regular algebra of global dimension d with Nakayama automorphism ν. Let be an iterated skew polynomial ring (see (21, Page 23)), with σ
i
graded. A is a skew PBW extension of R with relations x
i
r = σ
i
(r)x
i
and x
j
x
i
= x
i
x
j
, for r ∈ R and 1 ≤ i, j ≤n. As R is graded and c
i,j
= 1 ∈ R
0, then by Proposition 2.3 we have that A is a graded quasi-commutative skew PBW extension of R. Therefore, A is a graded skew Calabi-Yau algebra (Corollary 3.1). By Proposition 2.4,
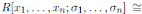
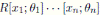 , where θ
j
(r) = σ
j
(r) and θ
j
(x
i
) = x
i
for i < j. Applying Theorem 3.1 we have that the Nakayama automorphism µ of A is given by µ(r) = (σ
1 · · · σ
n
)−1
ν(r), if r ∈ R and µ(x
i
) =
, where θ
j
(r) = σ
j
(r) and θ
j
(x
i
) = x
i
for i < j. Applying Theorem 3.1 we have that the Nakayama automorphism µ of A is given by µ(r) = (σ
1 · · · σ
n
)−1
ν(r), if r ∈ R and µ(x
i
) =
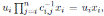
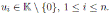
Example 3.2. For a fixed
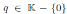 , the algebra of linear partial q-dilation operators H, with polynomial coefficients, is the free algebra
, the algebra of linear partial q-dilation operators H, with polynomial coefficients, is the free algebra
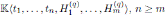 , subject to the relations:
, subject to the relations:
The algebra H is a graded quasi-commutative skew PBW extension of
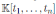 , where
, where
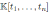 is endowed with usual graduation. According to Proposition 2.1, we have that
is endowed with usual graduation. According to Proposition 2.1, we have that
By Proposition 2.4, H is isomorphic to a graded iterated Ore extension of endomorphism type
with
Since
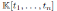 is a graded Calabi-Yau algebra, then its Nakayama automorphism ν is the identity map. Applying Theorem 3.1, we have that the Nakayama automorphism µ of H is given by
is a graded Calabi-Yau algebra, then its Nakayama automorphism ν is the identity map. Applying Theorem 3.1, we have that the Nakayama automorphism µ of H is given by
So, det(M ) = q. By Corollary 3.3 we have that the Nakayama automorphism µ of H is given by
Therefore, the Nakayama automorphism of H is completely determined by the parameter q.
4 Nakayama automorphism of some specific skew PBW extensions
Liu and Ma in [6] computed the Nakayama automorphism for Ore extensions over a polynomial algebra in n variables. Since Ore extensions of bijective type are skew PBW extensions, in this section we use these results to calculate explicitly the Nakayama automorphism of some skew PBW extensions of the form
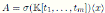 , which are not quasicommutative.
, which are not quasicommutative.
Next we present (6, Theorem 4.2), but using the notation of skew PBW extensions.
Theorem 4.1. Let
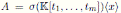 be a skew PBW extension of derivation type. The Nakayama automorphism ν of A is then given by ν(r)= r for all r ∈ R and
be a skew PBW extension of derivation type. The Nakayama automorphism ν of A is then given by ν(r)= r for all r ∈ R and
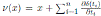 , where δ is as in Proposition 2.1.
, where δ is as in Proposition 2.1.
Next we calculate the Nakayama automorphism of a skew PBW extension of derivation type using Theorem 4.1. This automorphism had already been calculated by other authors using other techniques (see for example [2] or [22]).
Example 4.1. Let
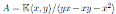 be the Jordan plane. Note that
be the Jordan plane. Note that
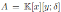 is a graded skew PBW extension of
is a graded skew PBW extension of
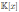 of derivation type, with δ(x) = x
2. By Theorem 4.1 we have that the Nakayama automorphism of A is given by
of derivation type, with δ(x) = x
2. By Theorem 4.1 we have that the Nakayama automorphism of A is given by
If the Nakayama automorphism of a skew Calabi-Yau algebra A is the identity then A is Calabi-Yau. Thus, from Theorem 4.1 the following are obtained immediately.
Corollary 4.1. Let
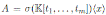 be a skew PBW extension. Then A is Calabi-Yau if and only if σ = id and
be a skew PBW extension. Then A is Calabi-Yau if and only if σ = id and
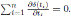
Example 4.2. The first Weyl algebra
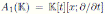 is a skew PBW extension of derivation type which is not graded. Note that xt = tx + 1, then δ(t) = 1 and
is a skew PBW extension of derivation type which is not graded. Note that xt = tx + 1, then δ(t) = 1 and
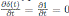 . By Corollary 4.1 we have that A
1(K) is a Calabi-Yau algebra, which was already known but using other techniques (see for example [23]).
. By Corollary 4.1 we have that A
1(K) is a Calabi-Yau algebra, which was already known but using other techniques (see for example [23]).
Liu and Ma in (6, Lemma 4.4) proved that for the Ore extension
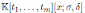 with σ ƒ= id, there is a unique k in the quotient field
with σ ƒ= id, there is a unique k in the quotient field
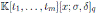 of
of
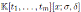 such that
such that
Next we present (6, Theorem 4.5), but using the notation of skew PBW extensions.
Theorem 4.2. Let
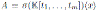 be a graded skew PBW extension with
be a graded skew PBW extension with
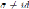 . Then the Nakayama automorphism ν of A is given by
. Then the Nakayama automorphism ν of A is given by
where M is as in (8), k is as in (9) and σ
q
is the extension of σ to 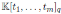 .
.
Lü, Mao and Zhang in [3] calculated the Nakayama automorphism for the following classes of algebras:
where K is an algebraically closed field of characteristic zero and p12, p13, p23, p, q ∈
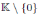 . Notice that these algebras are graded skew PBW extensions. In the following proposition we calculate the Nakayama automorphism of A(2) using Theorem 4.2.
. Notice that these algebras are graded skew PBW extensions. In the following proposition we calculate the Nakayama automorphism of A(2) using Theorem 4.2.
Proposition 4.1. The Nakayama automorphism ν of A(2) is given by
 .
.
Proof. Since
 and
and
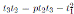 , then A(2) is a graded skew PBW extension of
, then A(2) is a graded skew PBW extension of
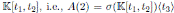 . Note that
. Note that
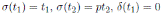 and
and
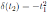 , where σ and δ are as in Proposition 2.1. Thus,
, where σ and δ are as in Proposition 2.1. Thus,
Note that
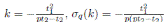 and
and
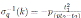 . Then by Theorem 4.2
. Then by Theorem 4.2
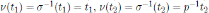 and ν(t
3) = det(M )t
3+ det(M )k − σq−1(k) =
and ν(t
3) = det(M )t
3+ det(M )k − σq−1(k) =
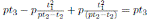
The Nakayama automorphism of Proposition 4.1 coincides with the Nakayama automorphism in (3, Equation (E1.5.2)).
5 Conclusions
There are some special subclasses of skew PBW extensions such as bijective, quasi-commutative, of derivation type and of endomorphism type (see Definition 2.2). Some noncommutative rings are skew PBW extensions but not Ore extensions (see [8],[9] and [10]). We illustrate each one of the properties studied here with some of these examples of skew PBW extensions.
From Proposition 3.1, if A is a graded quasi-commutative skew PBW extension of an Artin-Schelter regular algebra R, then A is Artin-Schelter regular. Now, for connected graded algebras, an algebra is Artin-Schelter regular if and only if this is graded skew Calabi-Yau (see 2.7). Therefore, if R is an Artin-Schelter regular algebra with Nakayama automorphism ν, then the Nakayama automorphism µ of a graded quasi-commutative skew PBW extension A exists, and we compute it using the Nakayama automorphism ν together some especial automorphisms of R and A (see Theorem 3.1). As a consequence of Theorem 3.1, we have that if
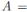
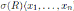 is a graded quasi-commutative skew PBW extension of an Artin-Schelter regular algebra R with Nakayama automorphism ν, then A is graded Calabi-Yau if and only if σ
1 · · · σ
n
= ν and
is a graded quasi-commutative skew PBW extension of an Artin-Schelter regular algebra R with Nakayama automorphism ν, then A is graded Calabi-Yau if and only if σ
1 · · · σ
n
= ν and
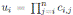 for all 1 ≤ i ≤ n (see Corollary 3.2). Another consequence of Theorem 3.1 is the fact that for
for all 1 ≤ i ≤ n (see Corollary 3.2). Another consequence of Theorem 3.1 is the fact that for
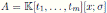 with σ be a graded algebra automorphism, u = det(M ), i.e., the element u is calculable (see Corollary 3.3).
with σ be a graded algebra automorphism, u = det(M ), i.e., the element u is calculable (see Corollary 3.3).
Most authors give a description of the Nakayama automorphism of some specific Artin-Schelter regular algebras in terms of some parameters that can not be calculated explicitly (see for example [2],[5] and [24]). Since Ore extensions of bijective type are skew PBW extensions, in Section 4 is calculated explicitly the Nakayama automorphism of some skew PBW extensions (Examples 4.1, 4.2 and Proposition 4.1).