1 Introduction

The notion of a (Brandt) groupoid was first introduced in [¹] from an algebraic point of view. Later on, this notion was generalized by Ehresmann [²], who considered topological and differentiable structures. Yet another equivalent definition of groupoid (together with its properties) appears in [³], where a groupoid is defined as a small category for which each morphism is invertible. In [⁴] is studied the structure and the theory of representations of finite groupoids.

In [⁵], Definition 1.1), Ivan follows Ehresmann’s paper [²] and presents the notion of groupoid as a particular case of a universal algebra. In addition, he defines the notion of strong homomorphism for groupoids and proves the correspondence theorem (or the fourth isomorphism theorem), in this context. In addition, Cayley’s Theorem for groupoids can be found in [⁶], Theorem 3.1).

In [⁷], a union pseudogroup is defined using the category dual to the category of groupoids instead of the category of pseudospaces. In particular, the notion of groupoid is presented as a quadruple formed by a set and three relations: a multiplication, a star operation and a relation from one single set to the initial base set, satisfying four conditions. It is showed that this definition of groupoid is equivalent to the categorical definition. Stachura in [⁸] follows the definition given by Zakrzewski in [⁷] and presents some properties of morphisms of groupoids (denomined Zakrzewski morphisms) and shows a relation between Zakrzewski morphisms and groupoid actions.

The definition of groupoid from an axiomatic approach, similar to that of a group, is presented in [⁹]. In this sense, Paques and Tamusiunas [¹⁰] give necessary and sufficient conditions for a subgroupoid to be a normal subgroupoid and they construct the quotient groupoid. In [¹¹], the isomorphism theorems are proven and one application of them to the normal series is presented.

An ordered groupoid is a groupoid equipped with a partial order, which preserves inverses, products, and restrictions and corestrictions of identities. Recently, in [¹²] some homological properties of a relation defined on an ordered groupoid are presented. Further, if that relation is transitive then the respective quotient set is again an ordered groupoid.

The purpose of the present paper is to introduce several concepts into the theory of groupoids which are analogous to those for groups, such as, the center, normalizer, commutator, and inner isomorphism. In addition, the normality of these subgroupoids and their properties are studied. This paper is organized as follows. In Section 2, we present some preliminaries and basic results on groupoids and subgroupoids, which are used in the following sections. In Section 3, we present some algebraic properties of normal subgroupoids and define the normalizer NG (H) of a subgroupoid . Furthermore, we show that the normalizer is the greatest wide subgroupoid of the groupoid G in which H is normal (Proposition 3.3). In Section 4, we introduce the center Z(G) and the commutator subgroupoids G’ of G. We prove that both of them are normal subgroupoids and that G/G’ is the largest abelian quotient of G (Propositions 4.2 and 4.4). In Section 5, we introduce the groupoids A(G) and I(G), which are defined by all the partial isomorphisms and all the inner isomorphisms of G, respectively. Finally, we prove that I(G) is a normal subgroupoid of A(G) and that it is isomorphic to the quotient groupoid G/Z(G) (Proposition 5.2).

2 Preliminaries and basic results

Now, we will give the definition of a groupoid from a purely algebraic point of view. We follow the definition presented in [⁹].

Deftnition 2.1. [⁹], p. 78). Let G be a set equipped with a partial binary operation which is denoted by concatenation. If g, h ∈ G and if the product gh is defined, we write ∃gh. A element e ∈ G is called an identity if ∃eg implies eg = g and ∃g ^’ e implies g ^' e = g ^’ . Then is said to be a groupoid if the following axioms hold:

In the theory of groupoids it is important to characterize those cases for which the product of two elements exists. It can be proved that if x, y ∈ G, then ∃xy if, and only if, d(x) = r(y) [¹¹], Lemma 2.3). The following proposition states several important properties that are fulfilled by groupoids.

Proposition 2.2. [¹¹], Proposition 2.7). Let G be a groupoid. Then for each g, h, k, l ∈ G we have:

The following results are easily obtained from the previous proposition.

Proposition 2.3. [¹¹], Proposition 2.8). If is a groupoid and g ∈ G, then d(g) = r(g ⁻¹), d(d(g)) = d(g) = r(d(g)), and d(r(g)) = r(g) = r(r(g)).

Definition 2.4. Let G be a groupoid. The set of all the identities of G is denoted by G₀ .

The identities of the groupoid G are the elements e = d(g) with g ∈ G [¹¹], Proposition 2.10), and we set G₀ ={e = d(g) │ g ∈ G} . If e ∈ G₀, then by Proposition 2.3, we have that d(e) = r(e) = e, ∃ee, ee = e, and e ⁻¹ = e. That is, the set G _e = {g ∈ G│d(g) = r(g) = e} is a group with identity element e, which is called the isotropy group associated to e.

These isotropy groups are very important, since they allow us to extend some concepts from groups to groupoids. For example, a groupoid G is called abelian if all its isotropy groups are abelian [¹³], Definition 1.1). In this way, the set Iso(G) = U _e∈G0 G_e, which is called the isotropy subgroupoid of G, is essential in the study of groupoids.

Now, we will present the definitions of subgroupoid and wide subgroupoid and prove some algebraic properties of these substructures.

Deftnition 2.5. [¹⁰], p. 107. Let G be a groupoid and H a nonempty subset of G. Then H is said to be a subgroupoid of G if for all g, h ∈ H one has:

In this case, we write H < G. In addition, if H₀ = G₀ (or equivalently G₀ ⊆ H), then H is called a wide subgroupoid of G.

Note that if G is a groupoid, then the sets {d(g)} _g∈G , G _e for any e ∈ G₀, G₀, Iso(G) and G are subgroupoids of G. Also, it is easy to see that if H is a subgroupoid, then the set H ∪ G₀ is a wide subgroupoid of G.

Moreover, if H is a wide subgroupoid of G and if g ∈ G, then g ⁻¹Hg = {g ⁻¹ hg | h ∈ H and r(h) = d(h) = r(g)} is a subgroupoid of G. In fact, note that r(g) ∈ H and thus ∃g ⁻¹ r(g)g, that is, d(g) = g ⁻¹ r(g)g ∈ g ⁻¹ Hg. If x, y g ⁻¹ Hg, then x = g ⁻¹ hg, y = g ⁻¹ tg with h, t ∈ H , and r(h) = d(h) = r(t) = d(t) = r(g). Since d(g ⁻¹ hg) = d(g) = r(g ⁻¹) = r(g ⁻¹ tg), then ∃(g ⁻¹ hg)(g ⁻¹ tg) and it follows that xy = (g ⁻¹ hg)(g ⁻¹ tg) = (g ⁻¹ h)(r(g))(tg) = (g ⁻¹ h)(r(t)t)g = g ⁻¹ htg. Now, since ∃ht, then ht ∈ H and thus xy ∈ g ⁻¹Hg. Finally, if x ∈ G, then x = g ⁻¹ hg with h ∈ H and r(h) = d(h) = r(g). Thus, x ⁻¹ = g ⁻¹ h ⁻¹ g ∈ g ⁻¹Hg since h ⁻¹ ∈ H. Hence, the set g ⁻¹Hg is a subgroupoid of G. Note in particular that g ⁻¹Hg is a subgroup of G _d(g) and g ⁻¹Hg = g ⁻¹H _r(g) g.

The following proposition extends to the context of groupoids several elementary results for groups.

Proposition 2.6. Let G be a groupoid, {H _i } _i∈I a family of subgroupoids

of G, and ∅ = B ⊆ G. Then:

If G is a groupoid and ∅ = B ⊆ G, then the subgroupoid given in the previous proposition will be called the subgroupoid generated by B and it will be denoted by 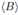. It can be proved that the set 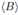is given by 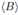= {x ₁ ^α 1 x ₂ ^α 2 ...x _n ^α n | ∃x ₁ ^α 1 x ₂ ^α 2 ...x _n ^α n , x _i ∈ B, α _i ∈ {1, −1} ∀i, n ∈ ℕ}. Also, note that 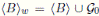is a wide subgroupoid; it will be called the wide subgroupoid generated by B.

set If G is a groupoid and H, K are wide subgroupoids of G, we define the

HK := {hk | d(h) = r(k), h ∈ H, k ∈ K}.

Note that G₀ ⊆ HK. In fact, d(g) = d(g)d(g) ∈ HK for each g ∈ G. Inparticular, HK≠∅.

Proposition 2.7. Let G be a groupoid and H, K be wide subgroupoids of G Then HK is a wide subgroupoid of G if, and only if, HK = KH.

Proof. Let x ∈ HK. By assumption, HK ≤ G and thus x ⁻¹ ∈ HK. Then x ⁻¹ = hk with h ∈ H, k ∈ K, d(h) = r(k) and hence x = (x ⁻¹)⁻¹ = (hk)⁻¹ = k ⁻¹ h ⁻¹ ∈ KH. On the other hand, G₀ ⊆ KH. If y ∈ KH, then y = kh with k ∈ K, h ∈ H, d(k) = r(h). Since k ⁻¹ ∈ K and h ⁻¹ ∈ H, then by assumption ∃h ⁻¹ k ⁻¹ and h ⁻¹ k ⁻¹ ∈ HK. Hence, y = kh = (h ⁻¹ k ⁻¹)⁻¹ ∈ HK.

Conversely, suppose that HK = KH. First note that HK ƒ= ∅. If x, y ∈ HK, then x = hk with h ∈ H, k ∈ K, and d(h) = r(k). Similarly, y = st with s ∈ H, t ∈ K, and d(s) = r(t). If ∃xy, then xy = (hk)(st) = h(ks)t = h(s ^’ k ^’)t = (hs ^’)(k ^’ t) ∈ HK and again d(hs ^’) = r(k ^’ t). Finally, if x ∈ HK, then x = hk with h ∈ H, k ∈ K, and d(h) = r(k). Thus x ⁻¹ = (hk)⁻¹ = k ⁻¹ h ⁻¹ ∈ KH ⊆ HK. That is, HK ≤ G and since G₀ ⊆ HK, we conclude that HK is a wide subgroupoid of G.

3 Normal subgroupoids

In this section, we present the concept of a normal subgroupoid and several properties of them. We also introduce the normalizer N_G(H) of a subgroupoid H and prove some of its algebraic properties. In particular, we prove that the normalizer is the greatest wide subgroupoid of G in which H is normal.

Definition 3.1. Let G be a groupoid. A subgroupoid H of G is said to be normal, written H ⊳ G, if H is wide and g ⁻¹Hg ⊆ H for all g ∈ G.

Note that G is a normal subgroupoid of G. Now, G₀ is a wide subgroupoid of G and if g ∈ G, then g ⁻¹G₀ g = {d(g)} ⊆ G₀. That is, G₀ is also a normal subgroupoid of G. Moreover, Iso(G) is a normal subgroupoid of G. If G is an abelian groupoid and H is a wide subgroupoid of G, then Iso(H) is normal in Iso(G).

Normality can also be characterized as follows [³]: A subgroupoid H is said to be normal if H₀ = G₀ and g ⁻¹ Hr(g)g = Hd(g) for all g ∈ G . The equivalence between both definitions of normality can be found in [¹⁰], Lemma 3.1.

The following proposition extends some well-known results from normal subgroups to normal subgroupoids. The proofs of items 1 and 2 are evident.

Proposition 3.2. Let G be a groupoid. Then:

Proof. 3. First note that HK ≠ ∅, since if h ∈ H, then h = hd(h) ∈ HK. Let x, y ∈ HK and assume that Ǝxy. Then x = hk, y = st with h, s ∈ H, k, t ∈ K, d(h) = r(k), and d(s) = r(t). Since Ǝxy, it follows that d(k) = r(s) and xy = (hk)(st) = hkst = hr(k)kst. Now, since r(k) = d(k) = r(s), we have that Ǝhr(s)kst and hr(s)kst = hss ⁻¹ kst = (hs)(s ⁻¹ ks)t ∈ HK. Finally, let x = hk with h ∈ H, k ∈ K and d(h) = r(k). Then x ⁻¹ = k ⁻¹ h ⁻¹ = d(k)k ⁻¹ h ⁻¹ and since d(k) = r(k) = d(h), we have that ∃d(h)k ⁻¹ h ⁻¹. Thus, x ⁻¹ = d(h)k ⁻¹ h ⁻¹ = h ⁻¹ hk ⁻¹ h ⁻¹ = h ⁻¹(hk ⁻¹ h ⁻¹) ∈ HK, whence the result follows.

4. By the previous item, HK is a subgroupoid of G. Let g ∈ G, h ∈ H, and k ∈ K with r(h) = d(k) = r(g) and d(h) = r(k). Then ∃g ⁻¹ hkg and we have that g ⁻¹ hkg = g ⁻¹ hr(k)kg = g ⁻¹ hr(g)kg = (g ⁻¹ hg)(g ⁻¹ kg) ∈ HK. That is, HK is a normal subgroupoid of G.

5. It is clear that H ∩ K is a wide subgroupoid of H. Let g ∈ H and h ∈ H ∩ K with r(h) = d(h) = r(g). Then ∃g ⁻¹ hg and since K is normal, we obtain that g ⁻¹ hg ∈ H ∩ K.

6. First, note that each d(g), g ∈ G, satisfies item 6 of this proposition. If h ∈ H and k ∈ K with r(h) = d(h) = r(k) = d(k), then ∃h ⁻¹ k ⁻¹ hk. Thus, we obtain that h ⁻¹ k ⁻¹ hk = h ⁻¹(k ⁻¹ hk) ∈ H and h ⁻¹ k ⁻¹ hk = (h ⁻¹ k ⁻¹ h)k ∈ K. Then, h ⁻¹ k ⁻¹ hk ∈ G₀, that is, h ⁻¹ k ⁻¹ hk = d(g) for some g ∈ G. Now, d(k) = d(h ⁻¹ k ⁻¹ hk) = d(g) and thus r(h) = d(h) = r(k) = d(k) = d(g). Hence, h ∈ Hd(g), k ∈ Kd(g) and the result follows from the theory of groups.

It is well known in the theory of groups that given a subgroup H, there exists the greatest subgroup of G in which H is normal [¹⁴]. Such a subgroup is known as the normalizer of H, and it satisfies several interesting properties. In our case, it is natural to ask if it is possible to define the normalizer of a subgroupoid. The answer to this question is affirmative as we show below.

If H is a wide subgroupoid of G, we define the set

N_G(H) = {g ∈ G | g ⁻¹H _r(g) g = H _d(g) },

which will be called the normalizer of H in G. It is clear that N_G(H) ≠ ∅ since for r(g) ∈ G₀, one has r(g)⁻¹H _r(r(g)) r(g) = r(g)H _r(g) r(g) = H _r(g) = Hd(r(g)), which implies that r(g) ∈ N_G(H). Therefore, G_{0 ʄ} ⊆ N_G(H). Note that in the case of a group, this concept coincides with the normalizer of a subgroup. The next proposition extends the main properties of the normalizer for groups to the groupoid setting.

Proposition 3.3. Let G be a groupoid and H a wide subgroupoid of G. Then:

Proof. 1. Note that the width of H was proved in the paragraph preceding the proposition. Now, if h ∈ H, then h ⁻¹H _r(h) h ⊆ H ∩ G _d(h) = H _d(h) . If m ∈ H _d(h) , then r(m) = d(m) = d(h), which implies that ∃hmh ⁻¹ and hmh ⁻¹ ∈ H _r(h) . Thus, ∃h ⁻¹(hmh ⁻¹)h and it is clear that m = h ⁻¹(hmh ⁻¹)h ∈ h ⁻¹H _r(h) h. Then, H _d(h) ⊆ h ⁻¹H _r(h) h and thus h ⁻¹H _r(h) h = H _d(h) , which implies h ∈ N_G(H). Hence, we conclude that H ⊆ N_G(H).

Let g, t ∈ N_G(H) and assume that ∃gt. Then g ⁻¹H _r(g) g = H _d(g) , t ⁻¹H _r(t) t = H _d(t) , d(g) = r(t), and thus

(gt)−1Hr(gt)(gt) = t−1g−1Hr(g)gt

= t−1Hd(g)t

= t−1Hr(t)t

= Hd(t)

= Hd(gt).

If t ∈ N_G(H), then t ⁻¹H _r(t) t = H _d(t) and thus tH _d(t) t ⁻¹ = H _r(t) . Hence, (t ⁻¹)⁻¹H _r(t −1)t ⁻¹ = H _d(t −1) and so t ⁻¹ ∈ N_G(H). Therefore, N_G(H) is a wide subgroupoid of G.

2. By item 1, H ⊆ N_G(H) and since H is a wide subgroupoid of G, we have that H is a wide subgroupoid of N_G(H). Now, assume m ∈ N_G(H), h ∈ H, and suppose that ∃m ⁻¹ hm. Then r(h) = d(h) = r(m), which implies h ∈ H _r(m) and thus m ⁻¹ hm ∈ m ⁻¹H _r(m) m = H _d(m) ⊆ H. Hence, H is normal in N_G(H).

3. Suppose that T is a wide subgroupoid of G and that H is normal in T . If t ∈ T , then t ⁻¹H _r(t) t = H _d(t) and thus t ∈ N_G(H). Hence, T ⊆ N_G(H) and the result follows.

4. This is evident.

Normal subgroups are very important in group theory, since they are necessary to construct the quotient group [¹⁴]. In the case of a groupoid, given a wide subgroupoid H of G, Paques and Tamusiunas [¹⁰] define a relation on G as follows: For every g, l ∈ G,

g ≡_H l ⇐⇒ (∃l ⁻¹ g and l ⁻¹ g ∈ H).

Furthermore, they prove that this relation is a congruence, that is, an equivalence relation which is compatible with the product. The equivalence class of ≡_H containing g is the set gH = {gh | h ∈ H ∧ r(h) = d(g)}. This set is called the left coset of H in G containing g. Moreover, they prove that if H is a normal subgroupoid of G and G/H is the set of all the left cosets of H in G, then G/H is a groupoid. The partial binary operation on G/H is given by ∃(gH)(lH) if, and only if, ∃gl and in this case, (gH)(lH) = glH [¹⁰], Lemma 3.12. This groupoid is called the quotient groupoid of G by H.

In order to improve the understanding of this topic, we finish this section by presenting the notion of a (strong) groupoid homomorphism and the first isomorphism theorem. The other isomorphism theorems also remain valid in our context of groupoids. The proofs of these theorems and several examples of them can be found in [¹¹].

Definition 3.4. Let G and G’ be groupoids. A map ɸ: G → G’ is called a groupoid homomorphism if for all x, y ∈ G, Ǝxy implies that Ǝɸ(x)ɸ(y) and in this case ɸ(xy) = ɸ(x)ɸ(y). In addition, if ɸ is a groupoid homomorphism and for all x, y ∈ G, Ǝɸ(x)ɸ(y) implies that Ǝxy, then ɸ is called a strong groupoid homomorphism.

Theorem 3.5. (The First Isomorphism Theorem) Let ɸ: G → G’ be a strong groupoid homomorphism. If ɸ is surjective, then there exists a strong isomorphism 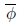: G/Ker(ɸ) →G’ such that ɸ = 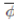◦ j, where j is the canonical homomorphism of G onto G/Ker(ɸ).

4 Center and commutators

In this section we introduce the notion of the center and the commutator subgroupoid, and prove several of their properties, which extend wellknown results for groups.

Definition 4.1. Let G be a groupoid. We define the center of G as the set Z(G) = {g ∈ Iso(G) | gh = hg for all h ∈ G such that d(g) = r(h) = d(h)}.

The center of has properties analogous to those for groups, as we show in the following proposition. Items 1 and 2 are evident.

Proposition 4.2. Let G be a groupoid and Z(G) the center of G. Then:

1. Z(G) =

2. Z(G) = Iso(G) if, and only if, G is an abelian groupoid;

3. Z(G) is a normal subgroupoid of Iso(G);

4. If H is a wide subgroupoid of Z(G), then it is normal in Iso(G).

Proof. 3. First of all, observe that G₀ ⊆ Z(G). Let g, h ∈ Z(G) and suppose that Ǝgh. Then by item 1, g ∈ Z(G_e) and h ∈ Z(G_e’) for some e, e ^’ ∈ G₀. Moreover, d(g) = r(g) = e and d(h) = r(h) = e ^’, and now since d(g) = r(h), we have e = e ^’. Thus h ∈ Z(G_e) and hence gh ∈ Z(G_e) ⊆ Z(G). If g ∈ Z(G), then g ∈ Z(G _e ) for some e ∈ G₀ and since Z(G_e) is a subgroup of G_e, we have g ⁻¹ ∈ Z(G_e) ⊆ Z(G). Thus Z(G) is a wide subgroupoid of G.

Finally, let g ∈ Iso(G) and h ∈ Z(G) be such that r(h) = d(h) = r(g). Then g ∈ G _e for some e ∈ G₀ and thus r(g) = d(g) = e, whence r(h) = d(h) = e. Thus h ∈ Z(G_e) and we have that g ⁻¹ hg = g ⁻¹ gh = d(g)h = eh = h ∈ Z(G). Hence, Z(G) is a normal subgroupoid of Iso(G).

Let g ∈ Iso(G) and h ∈ H be such that r(h) = d(h) = r(g). Then g ∈ G _e for some e ∈ G₀ and r(g) = d(g) = e. Thus r(h) = d(h) = e, h ∈ Z(G _e ), and since ∃g ⁻¹ hg we have that g ⁻¹ hg = g ⁻¹ gh = d(g)h = eh = h ∈ H. Hence, H is a normal subgroupoid of Iso(G).

If we wish to define the commutator subgroupoid of a groupoid G, then we must start by defining the commutator of two elements. Thus, if x, y ∈ G, then ∃xyx ⁻¹ y ⁻¹ if, and only if, d(x) = r(x) = d(y) = r(y), which is equivalent to x, y ∈ G _e for some e ∈ G₀. In particular, whenever x, y ∈ G _e for some e ∈ G₀, we define the commutator of x, y as [x, y] = x ⁻¹ y ⁻¹ xy.

Definition 4.3. Let G be a groupoid. The commutator subgroupoid of G is given by the set .

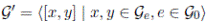Note that [x, y]⁻¹ = (x ⁻¹ y ⁻¹ xy)⁻¹ = [y, x] and d([x, y]) = r([x, y]) = e. Moreover, xy = yx[x, y ] and thus xy = yx if, and only if, [x, y ] = e. Finally, according to Proposition 2.6 the elements of G’ are all the finite products of commutators in G. That is, G’ = {x ₁ x ₂ · · · x _n | ∃x ₁ x ₂ · · · x _n , n ≥ 1 and each x _i is a commutator}.

More generally, if H, K are wide subgroupoids of G, then we define [H, K] = ([x, y] | x ∈ H _e , y ∈ K _e , e ∈ G₀). In particular, note that [H, K] = 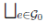[H _e ,K _e ] and G’= [G, G]. The main properties of the commutator subgroupoid are given in the following proposition. Note that all of them are valid for groups.

Proposition 4.4. Let G be a groupoid. Let x, y ∈ G _e and e ∈ G ₀ , and let further H be a wide subgroupoid of G. Then:

1. G’ =

2. G’ = G ₀ if, and only if, G is an abelian groupoid;

3. If H ⊳ G, then [H, G] ≤ H;

4. G’ is a normal subgroupoid of G and G / G’ is an abelian groupoid;

5. G / G’ is the largest abelian quotient of G in the sense that if H ⊳ G and G /H is abelian, then G’ ≤ H;

6. If σ: G → A is any homomorphism of G into an abelian groupoid A, then there exists a homomorphism θ: G / G’ → A such that σ = θ ◦ j, where j is the canonical homomorphism of G into G / G’.

Proof. 1. If a ∈ G’, then there exist commutators x ₁ , x ₂ , · · ·, x _n such that ∃x ₁ x ₂ · · · x _n and a = x ₁ x ₂ · · · x _n . Then x ₁ , x ₂ , · · ·, x _n ∈ G _e for some e ∈ G₀ and thus a ∈ G’ _e . The other inclusion is evident.

2. Let x, y ∈ G _e , e ∈ G₀. Then x ⁻¹ y ⁻¹ xy and thus x ⁻¹ y ⁻¹ xy ∈ G’. By assumption, x ⁻¹ y ⁻¹ xy = e and thus xy = yx. Hence, G _e is an abelian group.

Conversely, if G is an abelian groupoid, then for x, y ∈ G _e , x ⁻¹ y ⁻¹ xy = x ⁻¹ xy ⁻¹ y = d(x)d(y) = ee = e. Hence [x, y] = e.

3. Since [H, G] is a subgroupoid of G, it is enough to show that [H, G] ⊆ H Thus, if [x, y] ∈ [H, G], then x ∈ H _e , y ∈ G _e for some e ∈ G₀ and [x, y] = x ⁻¹ y ⁻¹ xy. By assumption, y ⁻¹ xy ∈ H and hence [x, y] ∈ H.

4. By item 1, G’ is a disjoint unionof groups, that is, G’ is a groupoid. Moreover, if e ∈ G₀, then e = [e, e] ∈ G and thus G’ is a wide subgroupoid of G. Let g ∈ G and a ∈ G’ be such that ∃g ⁻¹ ag. Then r(a) = d(a) = r(g) and a = [x ₁ , y ₁] [x ₂ , y ₂] [x _n , y _n ] where x _i , y _i ∈ G _e for some e ∈ G₀. Then gg ⁻¹ = r(g) = r(a) = d(a) = e and we obtain

g ⁻¹ ag = g ⁻¹[x ₁ , y ₁] [x ₂ , y ₂] · · · [x _n , y _n ]g

= g ⁻¹[x ₁ , y ₁]e[x ₂ , y ₂]e · · · e[x _n , y _n ]g

= g ⁻¹[x ₁ , y ₁]gg ⁻¹[x ₂ , y ₂]g · · · g ⁻¹[x _n , y _n ]g

= [g ⁻¹ x ₁ g, g ⁻¹ y ₁ g] [g ⁻¹ x ₂ g, g ⁻¹ y ₂ g] · · · [g ⁻¹ x _n g, g ⁻¹ y _n g] ∈ G’.

Hence, G’ is a normal subgroupoid of G.

Now, let x G’, y G’ ∈ (G/ G’) _eG j for some e G’ ∈ (G/ G’)₀. Then ∃(x G’)⁻¹(y G’)⁻¹ (x G’)(y G’) and (x G’)⁻¹(y G’)⁻¹(x G’)(y G’) = (x ⁻¹ G’)(y ⁻¹ G’)(x G’)(y G’) = (x ⁻¹ y ⁻¹ xy) G’ = e G’. This implies that (x G’)(y G’) = (y G’)(x G’), that is, (G/ G’) _eG’ is an abelian group.

5. Let [x, y] ∈ G’. Then x, y ∈ G _e for some e ∈ G₀. Now, [x, y]H = (x ⁻¹ y ⁻¹ xy)H = (x ⁻¹H)(y ⁻¹H)(xH)(yH) = (x ⁻¹H)(xH)(y ⁻¹H)(yH) = eH and hence [x, y]H = eH. That is, [x, y] ∈ H and so G’ ⊆ H.

6. First, note that if [x, y] ∈ G’, then x, y ∈ G _e for some e ∈ G₀. Thus r(x) = d(x) = r(y) = d(y) = e, which implies that r(σ(x)) = d(σ(x)) = r(σ(y)) = d(σ(y)) = σ(e) ∈ A _σ(e) . Then

σ([x, y]) = σ(x ⁻¹ y ⁻¹ xy)

= σ(x ⁻¹)σ(y ⁻¹)σ(x)σ(y)

= σ(x ⁻¹)σ(x)σ(y ⁻¹)σ(y)

= σ(e) ∈ A₀ .

Hence, G’ ⊆ Ker(σ). Now, we define θ: G/G’ → A by θ(xG’) = σ(x) for each xG/G’. If xG’= yG’, then Ǝy ⁻¹ x and y ⁻¹ x ∈ G’ ⊆ Ker(σ). Then σ(y ⁻¹ x) = σ(y)⁻¹ σ(x) = e ^’ for some e ^’ ∈ A₀, which implies that σ(x) = σ(y). Therefore, θ is a well defined function. Moreover, since σ is a homomorphism, θ is also a homomorphism and it is clear that σ = θ ◦j.

5 Inner isomorphisms

In this section we define the concepts of an inner isomorphism and a partial isomorphism of a groupoid, which are a natural generalizations of those for groups. We extend several results for these isomorphisms and in particular we prove that the set I(G) of all inner isomorphisms of G is a normal subgroupoid of the set A(G) of all partial isomorphisms of G. Moreover, we prove that the groupoid I(G) is isomorphic to the quotient groupoid G/Z(G), which generalizes a well-known result for groups.

If G is a groupoid, we define

A(G) = {f: G _e → G _e ’ | e, e ^’ ∈ G₀ and f is an isomorphism}.

Then for f, g ∈ A(G), we say that Ǝf g if, and only if, D(f ) = R(g), where D(f ) and R(g) denote the domain of f and the range of g, respectively. Moreover, in this case, (f ◦ g)(x) = f (g(x)) for all x ∈ D(g). With this partial operation, the set A(G) is a groupoid, where for f ∈ A(G) we have that d(f ) = idD(f ), r(f ) = idR(f ), and f ⁻¹ is the inverse of f . The elements of A(G) will be called partial isomorphisms of G. Note that if G is a group, then the set A(G) coincides with Aut(G).

In the group case, the notion of inner automorphism is very important in several subjects. The next results justify our generalization of this concept to groupoids and we extend several well-known results for groups.

Proposition 5.1. Let G be a groupoid and g ∈ G. Then the function I _g : G _d(g) → G _r(g) defined by I _g (x) = gxg ⁻¹ for all x ∈ G _d(g) is a partial isomorphism of G.

Proof. First, note that if x ∈ G _d(g) , then r(x) = d(x) = d(g), which implies that ∃gxg ⁻¹. Moreover, r(gxg ⁻¹) = r(g) and d(gxg ⁻¹) = d(g ⁻¹) = r(g) imply that gxg ⁻¹ ∈ G _r(g) . Thus, I _g is a well defined function. If x, y ∈ G _d(g) , then xy ∈ G _d(g) and thus

I _g (xy) = gxyg ⁻¹

= gxd(g)yg ⁻¹

= gxg ⁻¹ gyg ⁻¹

= I _g (x)I _g (y).

Hence, I _g is a homomorphism of groups and in particular, it is a strong homomorphism of groupoids. Now let x, y ∈ Gd(g) be such that I _g (x) = I _g (y). Then g ⁻¹ xg = g ⁻¹ yg and by the cancellation law (valid for groupoids), we obtain x = y. Whence, I _g is an injective function. If m ∈ G _r(g) , then r(m) = d(m) = r(g). This implies that ∃g ⁻¹ m, ∃mg, and thus ∃g ⁻¹ mg. Note that r(g ⁻¹ mg) = d(g ⁻¹ mg) = d(g) and so g ⁻¹ mg ∈ G _d(g) . Hence,

I _g (g ⁻¹ mg) = g(g ⁻¹ mg)g ⁻¹

= gg ⁻¹ mgg ⁻¹

= r(g)mr(g)

= m.

That is, I _g is a surjective function and we conclude that I _g is a strong partial isomorphism of . Note in particular that _g is an isomorphism of groups.

The isomorphisms given in Proposition 5.1 will be called partial inner isomorphisms of G, and the set of all inner isomorphisms of G will be denoted by I(G).

We say that a wide subgroupoid H of G is invariant by the partial inner isomorphism I _g , g ∈ G, if I _g (H ∩ D(I _g )) = H ∩ R(I _g ). That is, if Ig (Hr(g)) = Ig (H ∩ Gr(g)) = H ∩ Gd(g) = Hd(g).

Proposition 5.2. Let G be a groupoid and let H be a wide subgroupoid of G. Then:

Proof. 1. If e ∈ G₀, then the partial inner isomorphism I _e : G _e → G _e is given by I _e (x) = exe ⁻¹ = exe = x = id _Ge (x) for all x ∈ G _e . That is, I _e = id _G e , which implies that A(G)₀ ⊆ I(G).

Let I _g , I _h ∈ I(G) and suppose that ∃I _g ◦I _h . Then D(I _g ) = R(I_h), that is, G _d(g) = G _r(h) , and thus d(g) = r(h), which implies that ∃gh. Now, for x ∈ G _d(h) = G _d(gh) , we obtain (I _g ◦ I _h )(x) = I _g (I _h (x)) = g(hxh ⁻¹)g ⁻¹ = (gh)x(gh)⁻¹ = I _gh (x). That is, I _g ◦ I _h = I _gh ∈ I(G). Now, if I _g ∈ I(G), then I _g −1 ∈ I(G) and D(I _g ) = G _d(g) = G _r(g −1) = R(I_g−1 ). Thus, ∃I _g ◦ I _g −1 and I _g ◦ I _g −1 = I _r(g) = id _G r(g) . Also, D(I _g −1 ) = G _d(g −1) = G _r(g) = R(I_g), which implies that ∃I _g −1 ◦I _g and I _g −1 ◦I _g = I _d(g) = id _G d(g). Thus (I _g )⁻¹ = I _g −1 ∈ I(G), and hence I(G) is a wide subgroupoid of A(G).

Let σ ∈ A(G), I _g ∈ I(G), and suppose that ∃σ ⁻¹ ◦ I _g ◦ σ. Then R(I _g ) = D(I _g ) = R(σ) and thus G _r(g) = G _d(g) = R(σ) = D(σ ⁻¹). Hence, g, g ⁻¹ ∈ D(σ ⁻¹). Now, for x ∈ D(σ), we have that

(σ ⁻¹ ◦ I _g ◦ σ)(x) = σ ⁻¹(I _g (σ(x)))

= σ ⁻¹(gσ(x)g ⁻¹)

= σ ⁻¹(g)xσ ⁻¹(g ⁻¹)

= σ ⁻¹(g)x(σ ⁻¹(g))⁻¹

= I _σ −1(g)(x).

Hence σ ⁻¹ ◦I _g ◦σ = I _σ −1(g) ∈ I(G) and hence I(G) is a normal subgroupoid of A(G).

2. Let g ∈ G _e for some e ∈ G₀. Then the partial inner isomorphism I _g ∈ I(Iso(G)) and thus I _g = I _e j for some e ^j ∈ G₀. Then D(I _g ) = D(I _e j ) and R(I _g ) = R(I _e j ) and since r(g) = d(g) = e, we have that G _e = G _d(g) = G _r(g) = G _e j . Then e = e ^j and thus gxg ⁻¹ = I _g (x) = I _e (x) = x for all x ∈ G _e . That is, gx = xg for all x ∈ G _e . Thus G _e is an abelian group and hence G is an abelian groupoid.

On the other hand, assuming that G is abelian, let I _g ∈ I(Iso(G)), g ∈ G _e , and e ∈ G₀. Then d(g) = r(g) = e and thus for x ∈ G _e we have that I _g (x) = gxg ⁻¹ = gg ⁻¹ x = x = _e (x). That is, I _g = I _e , and the result follows.

3. If g, h ∈ G and ∃gh, then d(g) = r(h). Then D(Θ(g)) = D(I _g ) = G _d(g) = G _r(h) = R(I _h ) = R(Θ(h)) and thus ∃Θ(g) ◦ Θ(h). Now, if x ∈ D(I _gh ) = G _d(gh) = G _d(h) , then

Θ(gh)(x) = I _gh (x) = (gh)x(gh)⁻¹ = (gh)x(h ⁻¹ g ⁻¹)

= g(hxh ⁻¹)g ⁻¹ = I _g (I _h (x)) = (I _g ◦ I _h )(x)

= (Θ(g) ◦ Θ(h))(x).

That is, Θ(gh) = Θ(g)◦Θ(h) and hence Θ is a homomorphism of groupoids. Finally, let g, h ∈ G and suppose that ∃Θ(g) ◦ Θ(h). Then D(Θ(g)) = R(Θ(h)), that is, G _d(g) = Gr(h). We have that d(g) = r(h) and thus ∃gh. Hence, we conclude that Θ is a strong homomorphism.

4. First, note that the strong homomorphism Θ of item 3 is surjective. Now, we prove that Ker(Θ) = Z(G). If g ∈ Ker(Θ), then Θ(g) = I _g = I _e for some e ∈ G₀. Thus G _d(g) = D(I _g ) = D(I _e ) = G _e and therefore G _r(g) = R(I _g ) = R(I _e ) = G _e . Hence, G _d(g) = G _r(g) = G _e and we have that d(g) = r(g) = e. It follows that g ∈ G _e and gxg ⁻¹ = I _g (x) = I _e (x) = x for all x ∈ G _e , that is, gx = xg for all x ∈ G _e . Therefore, we conclude that g ∈ Z(G_e) ⊆ Z(G).

Finally, if g ∈ Z(G), then g ∈ Z(G _e ) for some e ∈ G₀. If x ∈ G _e , then I _g (x) = gxg ⁻¹ = xgg ⁻¹ = x = I _e (x). That is, Θ(g) = I _g = I _e ∈ I(G)₀.

Then by using the first isomorphism theorem (Theorem 3.5), we conclude that G/Z(G) is isomorphic to I(G).

5. It is evident.

6 Conclusions

The theory of groupoids has been developed over the last hundred years. This notion was given by Brand in 1926 [¹]. A groupoid can be presented from categories, algebraic structures, and universal algebra. In the last setting, the concept of congruence is well-known, but in this article we present an algebraic study on normal subgroupoids. We also improve this study by introducing several concepts related to normal subgroupoids which are analogous to those for groups, such as, the center, normalizer, commutator, and inner isomorphism, which are not found in the literature. We prove the normality of these subgroupoids and establish others properties. In particular, we define the normalizer N_G(H) of a subgroupoid H and prove that it is the greatest wide subgroupoid of the groupoid G in which H is normal (Proposition 3.3). Furthermore, we introduce the center Z(G) and the commutator subgroupoid G’ of G. We show that both of them are normal subgroupoids and that G/G’ is the largest abelian quotient of G (Propositions 4.2 and 4.4). We also introduce the groupoids A(G) and I(G), which are defined as all the partial isomorphisms and all the inner isomorphisms of G, respectively. Finally, we prove that I(G) is a normal subgroupoid of A(G) and that it is isomorphic to the quotient groupoid G/Z(G) (Proposition 5.2).