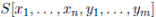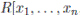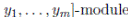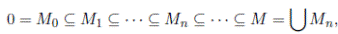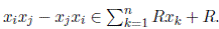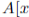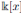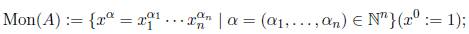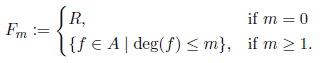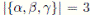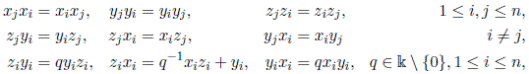1 Introduction
Hilbert’s Nullstellensatz is one of the three fundamental theorems about polynomial rings over fields. The two other theorems are Hilbert’s basis theorem that asserts that polynomial rings over fields are Noetherian, and Hilbert’s syzygy theorem that concerns the relations, or syzygies in Hilbert’s terminology, between the generators of an ideal, or, more generally, a module. Several formulations of the Nullstellensatz have been given throughout history. The most important formulation establishes a relationship between the radical of a polynomial ideal and the ideal of a variety of a polynomial ideal over the affine space. More precisely,
Proposition 1.1 ([1]. Theorem 4.2.6. (Strong Nullstellensatz)). Let
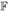 be an algebraically closed field. If I is an ideal in
be an algebraically closed field. If I is an ideal in
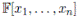 , then
, then
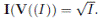
If we think of a version of the Hilbert’s Nullstellensatz for non-commutative rings of polynomial type, and throughout we can notice that Proposition 1,1 has several problems when we want to define a notion of variety since we have to switch the indeterminates, for this reason, in this paper we adopt an algebraic point of view with the aim of establishing the theorem for non-commutative algebraic structures. Our starting point is the following key fact about algebraic extensions of fields which is considered as the Hilbert’s Nullstellensatz in the commutative case. In fact Proposition 7.9 in Atiyah’s book is a previous result to the weak Nullstellensatz, which is Corollary 7.10.
Proposition 1.2 ([2], Proposition 7.9. (Hilbert’s Nullstellensatz)). Let
 be a field and E a finitely generated
be a field and E a finitely generated
 -algebra. If E is a field then it is a finite algebraic extension of
-algebra. If E is a field then it is a finite algebraic extension of
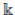 .
.
We can note that this version of Hilbert’s Nullstellensatz does not use the notion of variety; it only includes algebraic properties.
With this result in mind, our purpose in this paper is to present several algebraic formulations to Hilbert’s Nullstellensatz which have been given in the literature and cross out remarkable examples of non-commutative algebras appearing in mathematics and theoretical physics. More precisely, in Section 2 we consider all these algebraic formulations following their historical development. Finally, in Section 3, we illustrate the theorem considering the family of non-commutative rings known as skew Poincaré-Birkhoff-Witt extensions.
2 Algebraic formulations
One of the most important approaches for the non-commutative formulation of the Nullstellensatz is presented by Irving in [3]. There, we can find a relation between Hilbert’s Nullstellensatz for the Ore extensions defined by Ore [4] and the generic flatness condition (see Definition 2.5). Let us see the details.
Definition 2.1 ([5], page 60). Let R be a ring and I an ideal of R. We say that I is a left (right) primitive ideal, if there exists a simple left (right) R-module M such that Ann(M ) = I (the annihilator of M ). A right (left) primitive ring is any ring in which 0 is a right (left) primitive ideal, i.e., any ring which has a faithful simple right (left) module.
Definition 2.2 ([6], page 342). R is a Jacobson ring, if every prime ideal in R is an intersection of primitive ideals.
In particular, the nilradical of any ideal in a Jacobson ring coincides with the Jacobson radical. This property is the usual definition of a Jacobson ring ([2], page 71) and it is the one used in the context of non-commutative rings. In addition, there are other characterizations of Jacobson rings. For example, a ring R is a Jacobson ring if J (R/P ) = 0 (the Jacobson radical), for every prime ideal P of R. With this definition, we can see some examples of Jacobson rings, such as
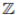 or
or
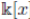 , with k a field. Of course, note that every field is a Jacobson ring.
, with k a field. Of course, note that every field is a Jacobson ring.
It is well-known that for commutative rings primitive ideals coincide with maximal ideals, whence a Jacobson ring is one in which every prime ideal is an intersection of maximal ideals. The most important property of the Jacobson ring establishes a relationship between a ring and its ring of polynomials as the following proposition shows.
Proposition 2.1 ([3], Proposition 2). If R is a Jacobson ring, so is the polynomial ring
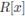 .
.
Proposition 2.1 can be used to deduce the Hilbert’s Nullstellensatz, and it could be considered a version of the Nullstellensatz. We might think that for the non-commutative rings introduced by Ore [4], if we start from a Jacobson ring and the extension of this ring is also a Jacobson ring we could conclude the Nullstellensatz. Unfortunately, at least in the Ore extensions, this result does not hold. Several authors have shown that non-commutative extensions of Jacobson rings which are not necessarily Jacobson (e.g., [3],[7] and [8]). In [9], under suitable conditions, Nasr-Isfahani and Moussavi proved that an Ore extension of a Jacobson ring is also Jacobson. This fact tells us that to extend Jacobson’s property we have to consider some other notions.
First of all, recall that a prime ideal P of a ring B (not necessarily commutative) is said to be a G-ideal, if the primes which properly contain P intersect in an ideal properly containing P . In this way, a commutative ring R is a G-domain if {0} is a G-ideal (the G-ideals of a commutative ring intersect in the nilradical), and R is called a Jacobson ring if every G-ideal is maximal (for more details, see [3], p. 260).
Definition 2.3 ([3], page 261). Let R be a commutative ring and A an R-algebra. We say that A satisfies the (right) strong Nullstellensatz, if for every simple right A-module M , the annihilator I intersects R in a G-ideal.
Definition 2.4 ([3], page 262). Let A be an algebra over a field
 . It is said that A satisfies the Nullstellensatz, if for any simple right A-module M , the division ring End
A
(M ) is algebraic over
. It is said that A satisfies the Nullstellensatz, if for any simple right A-module M , the division ring End
A
(M ) is algebraic over
 .
.
Definition 2.4 extends Proposition 1.2: Let K be a finitely-generated algebra over
 . Then K is a simple K-module, which equals its own endomorphism ring, and hence we have the algebraic version of the Hilbert’s Nullstellensatz.
. Then K is a simple K-module, which equals its own endomorphism ring, and hence we have the algebraic version of the Hilbert’s Nullstellensatz.
The use of the word “strong” is justified by Proposition 2.2.
Proposition 2.2 ([3], Proposition 3). Let A be an algebra over a field
 . If
. If
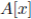 satisfies the strong Nullstellensatz as a
satisfies the strong Nullstellensatz as a
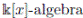 , then A satisfies the Nullstellensatz.
, then A satisfies the Nullstellensatz.
Proof. We follow the ideas presented by Irving in [3] with the aim of showing the importance of G-ideals. Let M be a simple A-module and let
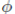 be an A-endomorphism of M . Note that M is an
be an A-endomorphism of M . Note that M is an
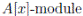 with x acting as
with x acting as
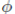 does. By Definition 2.3, some G-ideal of
does. By Definition 2.3, some G-ideal of
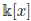 annihilates M , and since
annihilates M , and since
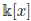 is not a G-domain then every G-ideal of
is not a G-domain then every G-ideal of
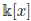 is maximal, whence for some non-zero polynomial
is maximal, whence for some non-zero polynomial
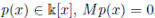 . Of course, this fact means that p(x) is the zero endomorphism, that is,
. Of course, this fact means that p(x) is the zero endomorphism, that is,
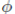 is algebraic over
is algebraic over
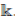 .
.
We have a more general version of the Nullstellensatz, even for the non-commutative case. However, in general, it is not easy to verify. Hence we will develop several tools in order to make such verification easier. For that, we recall the notion of generic flatness.
Definition 2.5 ([3], page 263). We say that an algebra A over a commutative domain R satisfies generic flatness, if for any finitely-generated A-module M , there exists a non-zero element c ∈ R such that the module M c = M ⊗ R R c is free over the localization R c .
We identify a relationship between generic flatness and the Nullstellensatz. This interaction is presented in [10] and justified in [3].
Proposition 2.3 ([3], Proposition 4). Let R be a commutative ring and A an R algebra. Suppose that for each prime P of R, the R/P -algebra A/PA satisfies generic flatness. Then A satisfies the strong Nullstellensatz.
Propositions 2.2 and 2.3 imply the following corollary.
Corollary 2.1 ([3], page 266). Let A be an algebra over the field
 and assume that
and assume that
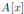 satisfies generic flatness as a
satisfies generic flatness as a
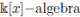 . Then A satisfies the Nullstellensatz.
. Then A satisfies the Nullstellensatz.
The following proposition establishes sufficient conditions to guarantee that an R-algebra is a Jacobson ring.
Proposition 2.4 ([3], Proposition 5). Let R be a commutative, Jacobosn ring and A an R-algebra which satisfies the strong Nullstellensatz. Assume that for each maximal ideal
 of R, the algebra
of R, the algebra
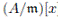 satisfies the Nullstellensatz over
satisfies the Nullstellensatz over
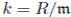 . Then the Jacobson radical of A is nilpotent. In particular if A is Noetherian, then A is a Jacobson ring.
. Then the Jacobson radical of A is nilpotent. In particular if A is Noetherian, then A is a Jacobson ring.
As we have seen, if one wants to verify the Nullstellensatz it is enough to check the condition of generic flatness. In the particular case of Ore extensions, we shall prove that these rings satisfy generic flatness. For that, let us recall its definition.
Definition 2.6 ([4]; [5], page 34). Let A be a ring, σ a ring endomorphism of A, and δ a σ-derivation on A (δ is a homomorphism of abelian groups satisfying δ(a
1
a
2) = σ(a
1)δ(a
2) + δ(a
1)a
2, for every a
1
, a
2 ∈ A). We shall write
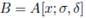 provided
provided
B is a ring, containing A as a subring;
x is an element of B;
B is a free left A-module with basis {1, x, x 2 , . . .};
xa = σ(a)x + δ(a), for all a ∈ A.
Such a ring B is called an Ore extension over A. If σ is injective, B is called an Ore extension of injective type.
When we have σ an automorphism, any element of B can be written either as a polynomial in x with all its coefficients on the left or as a polynomial with all its coefficients on the right. If A is an algebra over a commutative ring R, we want B to be an R-algebra as well. This will be the case if σ is an R-automorphism and δ vanishes on R.
We want to extend from the coefficient ring the property of generic flatness to the Ore extension. We will do it by guaranteeing that the extension is an algebra.
Proposition 2.5 ([3], Theorem 1). Let R be a commutative domain, and let A be a right Noetherian R-algebra which satisfies right generic flatness. Let σ be an R-automorphism of A and δ a σ-derivation such that δ(R) = 0. Then the Ore extension
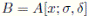 satisfies right generic flatness.
satisfies right generic flatness.
We can note that a Noetherian Ore extension with derivation zero in every element of a commutative domain satisfies generic flatness. This result is easy to extend in the following sense: Let R be a commutative Noetherian domain and A an R-algebra obtained from R by a finite succession of Ore extensions, each of which preserves the R-algebra structure. Then A satisfies generic flatness ([3], page 270). The following proposition is one of the most important results established in [3] about the Nullstellensatz and Jacobson’s property. We include its proof with the aim of showing the importance of the arguments involved there.
Proposition 2.6 ([3], Theorem 2). Let A be a finitely iterated Ore extension of the commutative Noetherian Jacobson ring R (field
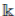 , respectively), which preserves the algebra structure. Then A satisfies the strong Nullstellensatz (the Nullstellensatz, respectively), and A is a Jacobson ring.
, respectively), which preserves the algebra structure. Then A satisfies the strong Nullstellensatz (the Nullstellensatz, respectively), and A is a Jacobson ring.
Proof. We follow the proof presented in [3]. If A is an R-algebra, the argument above on finite succession of Ore extensions guarantees that the assumptions of Proposition 2.3 hold, so A satisfies the strong Nullstellensatz.
Now, if A is an algebra over the field
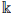 , the ring
, the ring
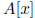 can be viewed as an iterated Ore extension of
can be viewed as an iterated Ore extension of
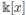 . Again, the argument on finite succession of Ore extensions implies that the hypotheses of Proposition 2.3 and Corollary 2.1 hold, so that A satisfies the Nullstellensatz.
. Again, the argument on finite succession of Ore extensions implies that the hypotheses of Proposition 2.3 and Corollary 2.1 hold, so that A satisfies the Nullstellensatz.
In either case, we consider Proposition 2.4 since
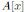 is an iterated Ore extension of R or
is an iterated Ore extension of R or
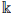 , whence
, whence
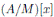 is an iterated Ore extension of
is an iterated Ore extension of
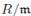 and satisfies the Nullstellensatz.
and satisfies the Nullstellensatz.
Since generic flatness and the strong Nullstellensatz are satisfied by remarkable families of finitely-generated Noetherian algebras, one might think that all finitely-generated Noetherian algebras satisfy these properties. However, this is not the case, as we can appreciate in the following example.
Example 2.1 ([3], Section IV). Consider the ring
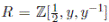 . Let T be the multiplicatively closed subset generated by the set of elements
. Let T be the multiplicatively closed subset generated by the set of elements
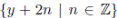 . Let S = R
T
be the corresponding localization. It is easy to see that S is a commutative, Noetherian, Jacobson ring, with an automorphism σ defined by σ(y) = y + 2. Consider the associated twisted group ring
. Let S = R
T
be the corresponding localization. It is easy to see that S is a commutative, Noetherian, Jacobson ring, with an automorphism σ defined by σ(y) = y + 2. Consider the associated twisted group ring
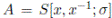 which consists of polynomials in x and x
−1
satisfying the relation x
−1
yx = y + 2, and, in general, x
−n
yx
n
= y + 2n and x
−n
y
−1
x
n
= (y + 2n)
−1
. Then A is a finitely-generated, Noetherian, Jacobson
which consists of polynomials in x and x
−1
satisfying the relation x
−1
yx = y + 2, and, in general, x
−n
yx
n
= y + 2n and x
−n
y
−1
x
n
= (y + 2n)
−1
. Then A is a finitely-generated, Noetherian, Jacobson
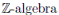 which is a primitive ring, and hence A does not satisfy the strong Nullstellensatz or generic flatness ([3], Theorem 3).
which is a primitive ring, and hence A does not satisfy the strong Nullstellensatz or generic flatness ([3], Theorem 3).
A second approach to the Hilbert’s Nullstellensatz in the noncommutative case was given by McConnell and Robson in [11]. This approach is an extended version of generic flatness to see how the theorem is satisfied in certain non-commutative affine algebras over a field. More precisely, in [11], p. 227, we can note that for certain non-commutative affine algebras R over a field /, if the following properties hold:
(Endomorphism property) For each simple right R-module M , End(M ) is algebraic over
, and,(Radical property) the Jacobson radical of each factor ring of R is nilpotent,
then, it is said that R satisfies the Nullstellensatz over
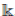 .
.
Next, we recall the definition of generic flatness given by McConnell and Robson [11] over a commutative integral domain D (compare with Definition 2.5).
Definition 2.7 ([11], Definition 1). We say that a D-algebra R is generically flat over D, if for each finitely generated right R-module M R , there exists 0 ≠ d ∈ D such that M d is free over D d .
There is a well-known connection between Definition 2.7 and the Nullstellensatz as we can see in [10], or Proposition 2.3 and Corollary 2.1.
About the notions of generically flatness, the endomorphism property and the Nullstellensatz, in (11, Lemmas 2 and 3), we can find some interesting relations: (i) Let R be a
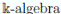 and x be a central indeterminate. If
and x be a central indeterminate. If
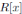 is generically flat over
is generically flat over
 then R has the endomorphism property. (ii) If R is a k-algebra, x is a central indeterminate and
then R has the endomorphism property. (ii) If R is a k-algebra, x is a central indeterminate and
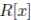 has the endomorphism property then R satisfies the Nullstellensatz. (iii) If R is a
has the endomorphism property then R satisfies the Nullstellensatz. (iii) If R is a
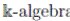 such that
such that
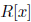 is generically flat over
is generically flat over
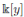 then R satisfies the Nullstellensatz.
then R satisfies the Nullstellensatz.
The following notion extends Definition 2.7.
Definition 2.8 ([11], Definition 5). A D-algebra R is (ℕ, ℕ)-generically flat over D, if
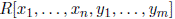 is generically flat over
is generically flat over
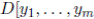 for all n, m ∈ ℕ.
for all n, m ∈ ℕ.
Lemma 2.1 ([11], Lemma 6). Let R ⊆ S be D-algebras and let R be (ℕ, ℕ)-generically flat over D. Suppose that either one of the following conditions holds:
S is a finite extension of R (i.e. S is finitely generated as a right R-module);
S is generated over R by an element z such that zR = Rz. Then S is (ℕ, ℕ)-generically flat over D.
Proof. Let us see the two cases.
We follow the proof presented in [11]. If we have that the algebraic structure
is a finitely generated
, then it is enough to prove that S is generically flat over D. Neverthless, any finitely generated right S-module is also finitely generated as a right R-module, so we are done.It is enough to show that S is generically flat over D, so by [6], page 349, we consider a cyclic S-module M , say M ∼= S/I, with I a right ideal of S. If one defines, for every n
I n = {r ∈ R | rz n ∈ z n−1 R + · · · + zR + R + I},
then one obtains a chain of R−modules
where
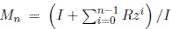 and M
n+1
/M
n
∼= R/I
n
as a D-module. Now, let
and M
n+1
/M
n
∼= R/I
n
as a D-module. Now, let
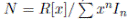 where x is a central indeterminate. N is a cyclic R [ x ] −module and so, by hypothesis, N
d
is free over D
d
for some 0 ≠ d ∈ D, here the condition (ℕ, ℕ)-generic flatness is needed). Thus each D
d
-direct summand (R/I
n
)
d
of N
d
is projective and hence M
d
splits, that is,
where x is a central indeterminate. N is a cyclic R [ x ] −module and so, by hypothesis, N
d
is free over D
d
for some 0 ≠ d ∈ D, here the condition (ℕ, ℕ)-generic flatness is needed). Thus each D
d
-direct summand (R/I
n
)
d
of N
d
is projective and hence M
d
splits, that is,
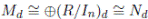 . Therefor M
d
is free.
. Therefor M
d
is free.
The following result establishes that for a filtered ring, the (ℕ, ℕ)-generically flat property inherits from its associated graded ring (see [6] for more details about filtered and graded rings).
Lemma 2.2 ([11], Lemma 7). Let S be a filtered D-algebra with D ⊆ S 0 and suppose that the associated graded ring Gr(S) is (ℕ, ℕ)-generically flat over D. Then so too is S.
Proof. It is sufficient to show that S is generically flat. If M is a finitely generated right S-module, it can be filtered so that Gr(M ) is finitely generated over Gr(S). Therefore (Gr(M )) d is free over D d for some d, and so, arguing as in Lemma 2.1 (ii), M d ∼= (Gr(M )) d and thus it is free.
In [11] it was shown that a kind of non-commutative rings are (ℕ, ℕ)-generically flat and so they satisfy the Nullstellensatz.
Definition 2.9 ([11], Definition 8). Let R, S be k-algebras (k a commutative ring) with R ⊂ S. S is an almost extension (also almost commutative algebra) of R, if the following conditions hold:
Lemma 2.3 ([11], Lemma 9). If R is (ℕ, ℕ)-generically flat over D and S is an almost normalizing extension of R then S is (ℕ, ℕ)-generically flat over D.
In [3] and [11] the definition of generically flat and generically free are used as the same. However, the two notions are not equivalent (recall that every free module is flat but the converse is not true).
A third approach to the subject was presented by Zhang et al. in [12]. In that paper, an R-module M is generically flat over a domain R if there is a simple localization R s such that M s = M ⊗R Rs is flat over R s . Generically projective and generically free modules are defined similarly.
A technique to verify that the modules over a fixed ring are generically free is to check that all the associated graded modules are generically projective as the following proposition establishes.
Proposition 2.7 ([12], Proposition 3.8). Let R be a commutative domain and let
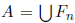 be an ℕ-filtered R-algebra. If every finite graded right Gr(A)-module is generically projective over R, then every finite right A-module is generically free over R.
be an ℕ-filtered R-algebra. If every finite graded right Gr(A)-module is generically projective over R, then every finite right A-module is generically free over R.
We recall the results of the previous subsections in the following lemma, in which, part (i) was established above and the part (ii) is a special case of Proposition 2.4.
Lemma 2.4 ([12], Lemma 3.9). Let A be a right Noetherian algebra over a field
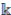 .
.
If every simple right
-module is generically free over
, then A satisfies the Nullstellensatz.If
satisfies the Nullstellensatz, then A is a Jacobson algebra.
With these new tools, we can give another approach of Nullstellensatz over the Ore extensions.
Proposition 2.8 ([12], Theorem 3.10). Let R be a commutative domain. Let A be a right Noetherian R-algebra such that every finite right A-module is generically free over R. Let
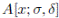 be an Ore extension for an R-linear automorphism σ and a R-linear σ-derivation δ. Then every finite right
be an Ore extension for an R-linear automorphism σ and a R-linear σ-derivation δ. Then every finite right
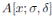 -module is generically free over R.
-module is generically free over R.
In order to state a result that helps us to describe the Hilbert’s Nullstellensatz, let us remind that an ℕ-graded R-algebra
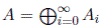 is called locally finite, if each homogeneous component A
i
is a finite R-module for every i.
is called locally finite, if each homogeneous component A
i
is a finite R-module for every i.
The following result is one of the most important theorems established in [12]. This will be very important in the next section.
Proposition 2.9 ([12], Theorem 0.4). Let A be an ℕ-filtered algebra over a field
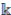 whose associated graded ring is locally finite and right Noetherian. Then A is a Jacobson algebra which satisfies the Nullstellensatz.
whose associated graded ring is locally finite and right Noetherian. Then A is a Jacobson algebra which satisfies the Nullstellensatz.
Remark 2.1 ([13], Proposition 2.10). Let A be a
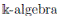 . A is finitely graded if and only if there exists a graded isomorphism of
. A is finitely graded if and only if there exists a graded isomorphism of
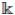 -algebras A ≅
-algebras A ≅
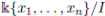 , where
, where
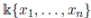 denotes the free algebra over k and I is a proper homogeneous two-sided ideal of
denotes the free algebra over k and I is a proper homogeneous two-sided ideal of
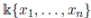 . In such case, A is locally finite, i.e., for every n ∈ ℕ, dimk
A
n
< ∞.
. In such case, A is locally finite, i.e., for every n ∈ ℕ, dimk
A
n
< ∞.
3 Examples
In this section, we illustrate with several examples the results established in the previous section. With this aim we will consider the family of non-commutative rings known as skew PBW extensiones. The reason for this choice is the attention that these objects have had in recent years (c.f. [14],[15],[16],[17],[18],[19],[20],[21] and [22]).
3.1 Skew Poincaré-Birkhoff-Witt extensions
Skew PBW (PBW denotes Poincaré-Birkhoff-Witt) extensions were defined in [23] as a generalization of PBW extensions introduced in [24]. During the last years several ring and homological properties of these extensions have been studied (e.g., [25],[26],[27],[28],[29] and [30]). For details about relations between these extensions and other non-commutative rings of polynomial type, see [31] or [32]. In particular, skew PBW extensions extend Ore extensions of injective type (as a matter of fact, in [33], Example 1, there are examples of skew PBW extensions which cannot be expressed as Ore extensions).
Definition 3.1 ([23], Definition 1). We say that A is a skew PBW extension of R (also called σ-PBW extension of R), which is denoted by A: = σ(R)(x 1 , . . . , x n ), if the following conditions hold:
(i). R is a subring of A sharing the same multiplicative identity element.
(ii). There exist elements x 1 , . . . , x n ∈ A such that A is a left free R-module, with basis the basic elements
(iii). For each 1 ≤ i ≤ n and any r ∈ R \ {0}, there exists an element c i,r ∈ R \ {0} such that x i r − c i,r x i ∈ R;
(iv). For any elements x i , x j with 1 ≤ i, j ≤ n, there exists c i,j ∈ R \ {0} such that x j x i − c i,j x i x j ∈ R + Rx 1 + · · · + Rx n .
Proposition 3.1 ([23], Proposition 3). Let A be a skew PBW extension of R. Then, for every 1 ≤ i ≤ n, there exist an injective ring endomorphism σ i : R → R and a σ i -derivation δ i : R → R such that x i r = σ i (r)x i + δ i (r), for each r ∈ R.
Proof. For every 1 ≤ i ≤ n and each r ∈ R we have elements c i,r , r i ∈ R such that x i r = c i,r x i + r i ; since Mon(A) is a R-basis of A c i,r and r i are unique for r, so we define σ i , δ i : R → R by σ i (r) = c i,r , δ i (r) = r i . We can check that σ i is a ring endomorphism and δ i is a σ i −derivation of R. For r, s ∈ R we have that
x i (r + s) = σ i (r + s)x i + δ i (r + s)
x i r + x i s = σ i (r)x i + δ i (r) + σ i (s)x i + δ(s)
= (σ i (r) + σ i (s))x i + δ i (r) + δ i (r),
so we have that σ i (r + s) = σ i (r) + σ i (s) and δ(r + s) = δ i (r) + δ i (r), and
x i (rs) = σ i (rs)x i + δ i (rs) (x i r)s = (σ i (r)x i + δ i (r))s
= σ i (r)x i s + δ i (r)s
= σ i (r)(σ i (s)x i + δ i (s)) + δ i (r)s
= σ i (r)σ i (s)x i + σ i (r)δ i (s) + δ i (r)s,
we have σ i (rs) = σ i (r)σ i (s) and δ i (rs) = σ i (r)δ i (s) + δ i (r)s (this is de condition of σ i -derivation), we can note also that x i = x i 1 = σ i (1)x i +δ i (1), so σ i (1) = 1 and δ i (1) = 0. Moreover, by the Definition 3.1 (iii), c i,r ƒ= 0 for r ƒ= 0. This means that σ i is injective.
Definition 3.2 ([23], Definition 4). Let A be a skew PBW extension.
(a). A is quasi-commutative, if the conditions (iii) and (iv) in the Definition 3.1 are replaced by the following:
(iii). For each 1 ≤ i ≤ n and any r ∈ R \ {0}, there exists an element c i,r ∈ R \ {0} such that x i r = c i,r x i .
(iv). For any elements x i , x j with 1 ≤ i, j ≤ n, there exists an element c i,j ∈ R \ {0} such that x j x i = c i,j x i x j .
(b). A is bijective, if σ i is bijective for every 1 ≤ i ≤ n and c i,j is invertible for any 1 ≤ i, j ≤ n.
Skew PBW extensions are filtered rings, as the following proposition shows.
Proposition 3.2 ([31], Theorem 2.2). Let A be an arbitrary skew PBW extension of R. Then, A is a filtered ring with filtration given by
and the corresponding graded ring Gr(A) is a quasi-commutative skew PBW extension of R. Moreover, if A is bijective, then Gr(A) is a quasi-commutative bijective skew PBW extension of R.
Proposition 3.3 ([31], Theorem 2.3). Let A be a quasi-commutative skew PBW extension of a ring R. (i) A is isomorphic to an iterated skew polynomial ring of endomorphism type. (ii) If A is bijective, then each endomorphism is bijective.
Corollary 3.1 ([31], Corollary 2.4. Hilbert Basis Theorem). Let A be a bijective skew PBW extension of R. If R is a left Noetherian ring, then A is also a left Noetherian ring.
The following are examples of skew PBW extensions (see [3] and [11] for a detailed definition of every algebraic structure): classical polynomial rings, skew polynomial rings of derivation type, the Weyl algebra, the universal enveloping algebra of a finite dimensional Lie algebra, the Woronowicz algebra, the q-Heisenberg algebra, the additive analogue of the Weyl algebra, the multiplicative analogue of the Weyl algebra. For all these examples we know that the Hilbert’s Nullstellensatz holds (see [31]).
Recall from Definition 2.4 that a
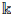 -algebra A satisfies the Nullstellensatz, if for any simple right A-module M , the division ring End
A
(M ) is algebraic over k. This will be our standard version of Hilbert’s Nullstellensatz that the following result extends for skew PBW extensions.
-algebra A satisfies the Nullstellensatz, if for any simple right A-module M , the division ring End
A
(M ) is algebraic over k. This will be our standard version of Hilbert’s Nullstellensatz that the following result extends for skew PBW extensions.
Proposition 3.4. Let R be a commutative domain. Let B be a right Noetherian R-algebra such that every finite right B-module is generically free over R. Let A be a skew PBW extension of B for an R-linear automorphism σ i and a R-linear σ i -derivation δ i , for 1 ≤ i ≤ n Then every finite right A-module is generically free over R.
Proof. Let A be a skew PBW extension of B, with B a right Noetherian R-algebra such that every finite right B-module is generically free over R. By Proposition 3.2 we know that Gr(A) is isomorphic to
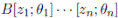 , and we have that θ
i
is a R-lineal automorphism, by hypothesis every finite right B module is generically free over R, whence Proposition 2.8 guarantees that every finite right
, and we have that θ
i
is a R-lineal automorphism, by hypothesis every finite right B module is generically free over R, whence Proposition 2.8 guarantees that every finite right
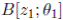 - module is generically free over R, so we can conclude that every finite right
- module is generically free over R, so we can conclude that every finite right
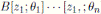 -module is generically free and by Proposition 2.7 we have that every finite right A-module is generically free over R.
-module is generically free and by Proposition 2.7 we have that every finite right A-module is generically free over R.
Following Proposition 2.9 we can give conditions that are sufficient for a skew PBW extension to satisfy Hilbert’s Nullstellensatz.
Theorem 3.1. Let A be a bijective skew PBW extension of a Noetherian
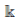 -algebra R such that A is also a
-algebra R such that A is also a
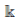 -algebra and Gr(A) is locally finite. Then A is a Jacobson algebra which satisfies the Nullstellensatz.
-algebra and Gr(A) is locally finite. Then A is a Jacobson algebra which satisfies the Nullstellensatz.
Proof. By Proposition 3.1, since A is a bijective skew PBW extension of R Noetherian, A is left Noetherian. According to Proposition 3.2, Gr(A) is a quasi-commutative bijective skew PBW extension isomorphic to an iterated skew polynomial ring
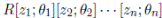 such that each θ
i
is bijective, 1 ≤ i ≤ n and by the Proposition 3.3 Gr(A) is left Noetherian, and by the hypothesis Gr(A) is locally finite. So we have A ℕ-filtered algebra over
such that each θ
i
is bijective, 1 ≤ i ≤ n and by the Proposition 3.3 Gr(A) is left Noetherian, and by the hypothesis Gr(A) is locally finite. So we have A ℕ-filtered algebra over
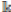 (Proposition 3.2) whose associated graded ring is locally finite and left Noetherian. Then, by Proposition 2.9, A is a Jacobson algebra which satisfies the Nullstellensatz.
(Proposition 3.2) whose associated graded ring is locally finite and left Noetherian. Then, by Proposition 2.9, A is a Jacobson algebra which satisfies the Nullstellensatz.
Corollary 3.2. Every bijective skew PBW extension which preserves the
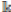 -algebra structure whose associated graded ring is finitely graded is a Jacobson algebra which satisfies the Nullstellensatz
-algebra structure whose associated graded ring is finitely graded is a Jacobson algebra which satisfies the Nullstellensatz
Proof. If we have A skew PBW extension over
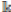 whose associated graded ring Gr(A) is finitely graded, by Remark 2.1. is locally finite and by Proposition 3.1 is left Noetherian. Then from the Theorem 3.1 A is a Jacobson algebra which satisfies the Nullstellensatz.
whose associated graded ring Gr(A) is finitely graded, by Remark 2.1. is locally finite and by Proposition 3.1 is left Noetherian. Then from the Theorem 3.1 A is a Jacobson algebra which satisfies the Nullstellensatz.
In the next section we will illustrate the Nullstellensatz with some particular examples of skew PBW extensions. As a matter of fact, ring and homological properties of these examples have been studied by several authors (c.f. [34],[35],[32],[33], [21],[36] and [13]).
3.1.1 Classical PBW extensions
Example 3.1 (Classical polynomial rings). Let
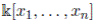 be the polynomial ring with
be the polynomial ring with
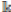 a field. The polynomial ring is an Ore extension with
a field. The polynomial ring is an Ore extension with
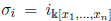 and δ
i
= 0, for 1 ≤ i ≤ n, Therefore, we have an extension over a Noetherian ring
and δ
i
= 0, for 1 ≤ i ≤ n, Therefore, we have an extension over a Noetherian ring
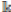 which preserves the algebra structure.
which preserves the algebra structure.
Then, polynomial ring satisfies the hypothesis of Proposition 2.6, whence the Nullstellensatz holds and it is a Jacobson algebra.
We can note also that
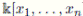 is an ℕ-filtered A algebra over
is an ℕ-filtered A algebra over
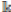 and its associated graded is
and its associated graded is
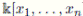 . We know that
. We know that
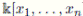 is Noetherian and locally finite. Then, for the Proposition 2.9
is Noetherian and locally finite. Then, for the Proposition 2.9
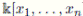 is a Jacobson algebra that satisfies the Nullstellensatz.
is a Jacobson algebra that satisfies the Nullstellensatz.
Finally, it is clear that the polynomial ring is a skew PBW extension. Since x
i
r − rx
i
= 0 and x
i
x
j
− x
j
x
i
= 0, for any r ∈ k and 1 ≤ i, j ≤ n. The k-free basis is Mon(
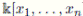 ). Every skew PBW extension is a filtered ring and its associated graded is locally finite. By Theorem 3.1,
). Every skew PBW extension is a filtered ring and its associated graded is locally finite. By Theorem 3.1,
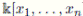 is a Jacobson algebra that satisfies the Nullstellensatz.
is a Jacobson algebra that satisfies the Nullstellensatz.
Example 3.2 (Universal enveloping algebra of a Lie algebra). Let
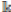 be a field and a finite dimensional Lie algebra over
be a field and a finite dimensional Lie algebra over
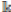 with basis {x
1
. . . , x
n
}. The universal enveloping algebra of , denoted by U(G), is not necessarily an Ore extension, and so we cannot conclude the Nustellensatz holds using Proposition 2.6. Now, in [37], page 75, it was shown that U(G) is an ℕ-filtered algebra. In [38], page 30, we can see that its associated graded is isomorphic to the classical polynomial ring. Therefore, this algebra is Noetherian and locally finite. Due to Proposition 2.9, U(G) is a Jacobson algebra that satisfies the Nullstellensatz.
with basis {x
1
. . . , x
n
}. The universal enveloping algebra of , denoted by U(G), is not necessarily an Ore extension, and so we cannot conclude the Nustellensatz holds using Proposition 2.6. Now, in [37], page 75, it was shown that U(G) is an ℕ-filtered algebra. In [38], page 30, we can see that its associated graded is isomorphic to the classical polynomial ring. Therefore, this algebra is Noetherian and locally finite. Due to Proposition 2.9, U(G) is a Jacobson algebra that satisfies the Nullstellensatz.
The universal enveloping algebra of G, U(G), can be seen as a skew PBW extension. In [31], page 1211, the authors shown that there exists a skew PBW extension
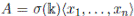 such that U(G) =∼ A. Since x
i
r − rx
i
= 0 and
such that U(G) =∼ A. Since x
i
r − rx
i
= 0 and
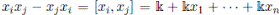 . In this case, A is an ℕ-filtered algebra and its associated graded is isomorphic to the classical polynomial ring and is locally finite. By Theorem, 3.1 A is a Jacobson algebra that satisfies the Nullstellensatz.
. In this case, A is an ℕ-filtered algebra and its associated graded is isomorphic to the classical polynomial ring and is locally finite. By Theorem, 3.1 A is a Jacobson algebra that satisfies the Nullstellensatz.
3.1.2 3-dimensional skew polynomial algebras Following [39], Definition C4.3, 3-dimensional skew polynomial algebras
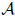 are
are
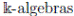 generated by the indeterminates x, y, z restricted to relations yz − αzy = λ, zx − βxz = µ, and xy − γyx = ν, such that the following conditions hold: (i)
generated by the indeterminates x, y, z restricted to relations yz − αzy = λ, zx − βxz = µ, and xy − γyx = ν, such that the following conditions hold: (i)
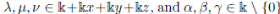 ; (ii) standard monomials, {x
i
y
j
z
k
| i, j, k ≥ 0}, are a k-basis of the algebra.
; (ii) standard monomials, {x
i
y
j
z
k
| i, j, k ≥ 0}, are a k-basis of the algebra.
From the definition, we can see that these algebras are skew PBW extensions; in fact, in [34] the authors shown that 3-dimensional skew polynomial algebras have a PBW basis and with the relations defined, we can note that these algebras satisfy the condition (iii) and (iv) of Definition 3.1 Note that 3 dimensional skew polynomials algebras are not necessarily PBW extensions in the sense of [24]. There exists a classification of 3-dimensional skew polynomial algebras, provided by [39], Theorem C.4.3.1. More precisely, up isomorphism,
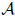 is one of the following algebras:
is one of the following algebras:
(a). if
, then
is defined by the relations yz − αzy = 0, zx − βxz = 0, and xy − γyx = 0.
(b). if α, β, γ = 2 and β = α = γ = 1, then is one of the following algebra:
(i). yz − zy = z, zx − βxz = y, xy − yx = x;
(ii). yz − zy = z, zx − βxz = b, xy − yx = x;
(iii). yz − zy = 0, zx − βxz = y, xy − yx = 0;
(iv). yz − zy = 0, zx − βxz = B, xy − yx = 0;
(v). yz − zy = az, zx − βxz = 0, xy − yx = x;
(vi). yz − zy = z, zx − βxz = 0, xy − yx = 0,
where a, b are any elements of k. All nonzero values of b yield isomorphic algebras.
(i). yz − αzy = 0, zx − βxz = y + b, and xy − γyx = 0;
(ii). yz − αzy = 0, zx − βxz = b, and xy − γyx = 0.
In this case, b ∈ k is an arbitrary element and, like before, any nonzero values of b give isomorphic algebras.
(d). If α = β = γ ≠ 1, then
is the algebra defined by the relations yz - αzy = a 1 x + b 1, zx - βxz = a 2 y + b 2, and xy - γyx = a 3 z + b 3 . If a i = 0 for i = 1, 2, 3, then all nonzero values of b i give isomorphic algebras.
(e). If α = β = γ = 1, then
is isomorphic to one of the following algebras:
(i). yz − zy = x, zx − xz = y, xy − yx = z;
(ii). yz − zy = 0, zx − xz = 0, xy − yx = z;
(iii). yz − zy = 0, zx − xz = 0, xy − yx = b;
(iv). yz − zy = −y, zx − xz = x + y, xy − yx = 0;
(v). yz − zy = az, zx − xz = z, xy − yx = 0;
With a, b ∈ k arbitrary, and all nonzero values of b generate isomorphic algebras.
Some of these algebras are not Ore extensions. For this reason we cannot use Proposition 2.6.3-dimensional skew polynomial algebras A are skew PBW extension as we remarked. From Proposition 3.2 we have that A is ℕ-filtered. The associated graded of this algebra is
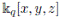 with q defined by an automorphism and is Noetherian and locally finite. By Proposition 2.9 or Theorem 3.1, the 3-dimensional skew polynomial algebras satisfy the Nullstellensatz.
with q defined by an automorphism and is Noetherian and locally finite. By Proposition 2.9 or Theorem 3.1, the 3-dimensional skew polynomial algebras satisfy the Nullstellensatz.
Example 3.3 (Dispin algebra U(osp(1, 2))). Dispin algebra U(osp(1, 2)), defined in [39], Definition C4.1, is the enveloping algebra of the Lie superalgebra osp(1, 2). It is generated by the indeterminates x, y, z over a field
 satisfying the relations yz zy = z, zx + xz = y, xy yx = x. This algebra is not an Ore extensions. Hence, we can not use Proposition 2.6 to conclude the Nullstellensatz.
satisfying the relations yz zy = z, zx + xz = y, xy yx = x. This algebra is not an Ore extensions. Hence, we can not use Proposition 2.6 to conclude the Nullstellensatz.
We can note that U (osp(1, 2)) is a skew PBW extension over
 ; in [31], page 1215, we note that U (osp(1, 2)) ∼=
; in [31], page 1215, we note that U (osp(1, 2)) ∼=
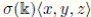 , its associated graded is
, its associated graded is
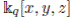 which is Noetherian and locally finite (indeed is a k-algebra finitely graded). Then, due to Proposition 2.9 or Theorem 3.1 U (osp(1, 2)) is a Jacobson algebra in which the Nullstellensatz holds.
which is Noetherian and locally finite (indeed is a k-algebra finitely graded). Then, due to Proposition 2.9 or Theorem 3.1 U (osp(1, 2)) is a Jacobson algebra in which the Nullstellensatz holds.
Example 3.4 (Woronowicz algebra
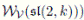 . This algebra was introduced by Woronowicz in [40] and redefined in [39] over an arbitrary field
. This algebra was introduced by Woronowicz in [40] and redefined in [39] over an arbitrary field
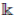 . It is generated by the indeterminates x, y, z subject to the relations xz − v
4
zx = (1 + v
2)x, xy − v
2
yx = vz, zy − v
4
yz = (1 + v
2)y, where
. It is generated by the indeterminates x, y, z subject to the relations xz − v
4
zx = (1 + v
2)x, xy − v
2
yx = vz, zy − v
4
yz = (1 + v
2)y, where
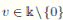 is not a root of unity. Since this algebra is not an Ore extension, we can not use Proposition 2.6 to conclude the Nullstellensatz.
is not a root of unity. Since this algebra is not an Ore extension, we can not use Proposition 2.6 to conclude the Nullstellensatz.
On the other hand, since
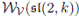 is a skew PBW extension over
is a skew PBW extension over
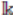 , i.e.,
, i.e.,
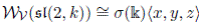 , its associated graded is
, its associated graded is
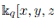 which is Noetherian and locally finite (indeed is a
which is Noetherian and locally finite (indeed is a
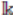 -algebra finitely graded). Then,due to Proposition 2.9 or Theorem 3.1,
-algebra finitely graded). Then,due to Proposition 2.9 or Theorem 3.1,
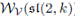 is a Jacobson algebra in which the Nullstellensatz holds.
is a Jacobson algebra in which the Nullstellensatz holds.
3.1.3 Other examples
Example 3.5 (Multiplicative analogue of the Weyl algebra). The k-algebra
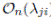 , defined in [41], is generated by the indeterminates x
1
, . . . , x
n
subject to the relations: x
j
x
i
= λ
ji
x
i
x
j
with 1 ≤ i < j ≤ n, and
, defined in [41], is generated by the indeterminates x
1
, . . . , x
n
subject to the relations: x
j
x
i
= λ
ji
x
i
x
j
with 1 ≤ i < j ≤ n, and
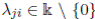 .
.
We can note that
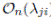 is not an Ore extension over
is not an Ore extension over
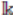 , but,
, but,
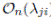 is an Ore extension over
is an Ore extension over
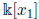 (see [38, page 29)). This is a finitely iterated Ore extension
(see [38, page 29)). This is a finitely iterated Ore extension
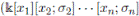 with
with
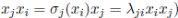 and we have that
and we have that
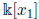 is a Jacobson ring, and preserves the algebra structure i.e. σ
i
(k) = k, for all k ∈
is a Jacobson ring, and preserves the algebra structure i.e. σ
i
(k) = k, for all k ∈
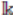 and we have that δ
i
= 0. Then, due to Proposition 2.6,
and we have that δ
i
= 0. Then, due to Proposition 2.6,
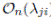 satisfies the Nullstellensatz .
satisfies the Nullstellensatz .
We can note for the relations that
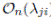 the condition (iii) of the Definition 3.1 and the condition (iv) (δ = 0). In [31], we can note that
the condition (iii) of the Definition 3.1 and the condition (iv) (δ = 0). In [31], we can note that
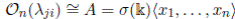 . A is N-filtered and its associated graded is
. A is N-filtered and its associated graded is
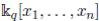 , its associated graded is Noetherian and locally finite. Then, by Proposition 2.9 or Theorem 3.1
, its associated graded is Noetherian and locally finite. Then, by Proposition 2.9 or Theorem 3.1
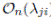 satisfies Nullstellensatz.
satisfies Nullstellensatz.
Example 3.6 (Additive analogue of the Weyl algebra). The
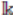 -algebra A
n
(q
1
, . . . , q
n
) is the algebra generated by the indeterminates x
1
, . . . , x
n
, y
1
, . . . , y
n
subject to the relations x
j
x
i
= x
i
x
j
and y
j
y
i
= y
i
y
j
for 1 ≤ i, j ≤ n, y
i
x
j
= x
j
y
i
for i ≠ j and y
i
x
i
= q
i
x
i
y
i
+ 1 for 1 ≤ i ≤ n, where
-algebra A
n
(q
1
, . . . , q
n
) is the algebra generated by the indeterminates x
1
, . . . , x
n
, y
1
, . . . , y
n
subject to the relations x
j
x
i
= x
i
x
j
and y
j
y
i
= y
i
y
j
for 1 ≤ i, j ≤ n, y
i
x
j
= x
j
y
i
for i ≠ j and y
i
x
i
= q
i
x
i
y
i
+ 1 for 1 ≤ i ≤ n, where
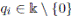 .
.
A
n
(q
1
, . . . , q
n
) is not an Ore extension over
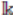 . In [38], the authors proved that this algebra is an Ore extension over
. In [38], the authors proved that this algebra is an Ore extension over
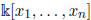 , i.e.
, i.e.
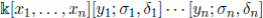 with y
i
x
i
= σ
i
(x
i
)y
i
+δ
i
(x
i
) = q
i
x
i
y
i
+ 1. Here, we have, for the Example 3.1 that
with y
i
x
i
= σ
i
(x
i
)y
i
+δ
i
(x
i
) = q
i
x
i
y
i
+ 1. Here, we have, for the Example 3.1 that
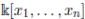 is a Jacobson ring and is commutative Noetherian ring. Then, due to Proposition 2.6 A
n
(q
1
, . . . , q
n
) satisfies the Nullstellensatz.
is a Jacobson ring and is commutative Noetherian ring. Then, due to Proposition 2.6 A
n
(q
1
, . . . , q
n
) satisfies the Nullstellensatz.
From the relations that describe the algebra, in [31] the authors shown that
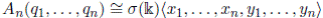 . Hence, the additive analogue of a Weyl algebra is a skew PBW extension. This algebra is ℕ-filteredand its associated graded is
. Hence, the additive analogue of a Weyl algebra is a skew PBW extension. This algebra is ℕ-filteredand its associated graded is
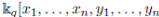 which is Noetherian and locally finite. Then, by Proposition 2.9 or Theorem 3.1, A
n
(q
1
, . . . , q
n
) satisfies Nullstellensatz.
which is Noetherian and locally finite. Then, by Proposition 2.9 or Theorem 3.1, A
n
(q
1
, . . . , q
n
) satisfies Nullstellensatz.
Example 3.7 (Quantum algebra). The k-algebra U' (so(3, k)), developed in [42] and [43] is generated by I
1
, I
2
, I
3 subject to relations I
2
I
1 − qI
1
I
2 =−q
1/2
I
3, I
3
I
1 − q
−1
I
1
I
3 = q
−1/2
I
2, I
3
I
2 − qI
2
I
3 = −q
1/2
I
1
, where q ∈
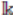 {0} . This algebra is not a Ore extension. Then, we can not conclude Nullstellensatz with Proposition 2.6.
{0} . This algebra is not a Ore extension. Then, we can not conclude Nullstellensatz with Proposition 2.6.
In [34] the authors proved that this algebra is a skew PBW extension
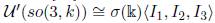 . Then we have that the algebra is ℕ-filtered and its associated graded is
. Then we have that the algebra is ℕ-filtered and its associated graded is
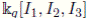 which is Noetherian and locally finite. Then, due to Proposition 2.9 or Theorem 3.1, U' (so(3, k)) satisfies Nullstellensatz.
which is Noetherian and locally finite. Then, due to Proposition 2.9 or Theorem 3.1, U' (so(3, k)) satisfies Nullstellensatz.
Example 3.8 (q-Heisenberg algebra). The
 -algebra H
n
(q) introduced in
-algebra H
n
(q) introduced in
[44] is generated by the set of variables x 1 , . . . , x n , y 1 , . . . , y n , z 1 , . . . , z n subject to the relations:
In [38], the authors proved that this algebra is an Ore extension over the commutative ring
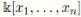 . Due to Proposition 2.6 we can conclude that H
n
(q) satisfies the Nullstellensatz.
. Due to Proposition 2.6 we can conclude that H
n
(q) satisfies the Nullstellensatz.
On the other hand [31] we can see that H
n
(q) is a skew PBW extension isomorphic to
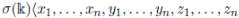 . This algebra is ℕ-filtered and its associated graded is
. This algebra is ℕ-filtered and its associated graded is
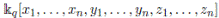 with q defined by the automorphisms σ
i
and θ
i
; its associated graded is Noetherian and locally finite. By Proposition 2.9 or Theorem 3.1, we conclude that H
n
(q) satisfies Nullstellensatz.
with q defined by the automorphisms σ
i
and θ
i
; its associated graded is Noetherian and locally finite. By Proposition 2.9 or Theorem 3.1, we conclude that H
n
(q) satisfies Nullstellensatz.
Example 3.9 (Jordan plane). The
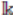 -algebra
-algebra
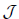 introduced in [45] is the free algebra defined by
introduced in [45] is the free algebra defined by
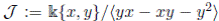 .
.
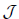 is a skew PBW extension of
is a skew PBW extension of
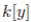 with the product given by xy = yx − y
2. This algebra is ℕ-filtered an its associated graded is
with the product given by xy = yx − y
2. This algebra is ℕ-filtered an its associated graded is
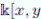 that is Noetherian and locally finite. Proposition 2.9 or Theorem 3.1 imply that H
n
(q) satisfies Nullstellensatz.
that is Noetherian and locally finite. Proposition 2.9 or Theorem 3.1 imply that H
n
(q) satisfies Nullstellensatz.
Remark 3.1. In [13], Remark 2.11, we can find another examples of skew PBW extensions that are locally finite (c.f. [20],[35] and [30]).