Conceptos psicométricos básicos

Se inicia el manuscrito con la definición de los conceptos de psicometría, instrumento de medida, medición y escala de medida para encuadrar los conceptos de confiabilidad y validez.

La psicometría es el campo de estudio concerniente a las teorías y técnicas de medición en psicología. En psicometría, el término de instrumento de medida hace referencia a un test o cuestionario formado por unas instrucciones verbales generales y unos ítems, reactivos o preguntas. Los ítems pueden ser verbales, lógicos, numéricos o materiales manipulables y requerir respuestas orales, escritas o ejecuciones de conductas observables (^{Kline, 2015}). A su vez, el formato de respuesta en los ítems puede ser cerrado, y usualmente homogéneo, o puede ser abierto. En este último caso, habría una codificación establecida para categorizar las respuestas, como en las escalas de conducta y las pruebas proyectivas (^{Piotrowski, 2015}). Unos instrumentos de medida requieren reportar conductas, ya sea públicamente observables o internas (sensaciones, deseos, motivos, emociones o pensamientos), las cuales son típicas o características de la persona; como es el caso de los test de personalidad, motivación, estado emocional o actitud. Otros instrumentos requieren resolver problemas, retener información, comprender información o mostrar conocimiento; como es el caso de los test de inteligencia, capacidad o funcionalidad (^{McClimans, Brown & Canoc, 2017}).

Las opciones de respuesta de los ítems del test se transforman en números bajo una regla estipulada. A este proceso de asignar números a las respuestas de los participantes se le denomina medición (^{Loewenthal & Lewis, 2018}).

La escala de medida de un ítem hace referencia a la correspondencia entre las propiedades empíricas de las distintas modalidades de respuesta y las propiedades algebraicas y operaciones aritméticas admisibles de los números asignados. Se distinguen cuatro tipos de escala de medida: nominal, ordinal, de intervalo o de razón (^{Wu & Leung, 2017}).

La escala de medida nominal asigna símbolos numéricos a los distintos atributos o modalidades cualitativas de respuesta. Estos números permiten contar frecuencias y contingencias, pero no admiten operaciones aritméticas ni poseen propiedades algebraicas. Usualmente es de tipo dicotómico, como por ejemplo, 0 = “no” y 1 = “sí” ante la ejecución de una conducta. Otro ejemplo sería: 0 = “conducta impropia del rasgo medido” y 1 = “conducta propia del rasgo”.

Una escala ordinal asigna números ordinales a las distintas categorías ordenables de las modalidades de respuesta. Estos números poseen propiedades de ordenación y conteo, así como posibilidad de aritmética ordinal de suma, multiplicación y exponenciación. Es la más usada en escalas de actitud y emociones e inventarios de personalidad y motivaciones. Un ejemplo sería: 1 = “nunca”, 2 = “a veces”, 3 = “con frecuencia”, 4 = “con mucha frecuencia” y 5 = “siempre” ante la frecuencia de una conducta.

Las escalas de medida también pueden ser de intervalo (por ejemplo, distancia desde el origen de la línea hasta el punto marcado en un continuo que va a 0 “nada” a 10 “insoportable” al evaluar el malestar provocado por un síntoma) o de razón (por ejemplo “tiempo de respuesta medido en milisegundos” o “número de veces que se repite una conducta en un intervalo de tiempo”). Estas dos escalas asignan números naturales, enteros, racionales, irracionales o reales a las distintas cantidades o magnitudes en que se presenta la respuesta. Estos números admiten operaciones aritméticas y poseen propiedades algebraicas, poseyendo los números reales las propiedades y posibilidades aritméticas más amplias o inclusivas. En la escala de intervalo, no se puede fijar un cero absoluto (ausencia del rasgo) y la unidad de medida solo permite medir distancias relativas entre puntos (intervalos), y en la escala de razón, se puede fijar el cero absoluto y las mediciones son absolutas desde este punto de origen.

La puntuación en el test se obtiene por la suma simple o el promedio de las puntuaciones en los ítems (^{Kline, 2015}; ^{Streiner, Norman & Cairney, 2015}). Las puntuaciones en el test pueden ser interpretadas en términos absolutos o relativos. En el primer caso, se usan el contenido de las categorías de respuesta. En el segundo caso, se usan como normas interpretativas las estimaciones de los parámetros de la distribución teórica a la que se aproximan las puntuaciones en una población, o se usan las estimaciones de los cuantiles poblacionales en caso de que la función de distribución empírica no siga ninguna función teórica reconocible (^{Loewenthal & Lewis, 2018}). Usualmente, las puntuaciones en los test de actitud, emociones, motivaciones y personalidad están en una escala de medida de intervalo (^{Wu & Leung, 2017}).

Confiabilidad y validez del instrumento de medida

Desde la teoría clásica de test, la confiabilidad de un instrumento de medida hace referencia a su capacidad de obtener mediciones con error mínimo (^{Jabrayilov, Emons & Sijtsma, 2016}). Se puede establecer a través de tres estrategias: confiabilidad temporal o correlaciones al aplicar el mismo instrumento en dos o más momentos distintos; confiabilidad interjuez o correlaciones entre las mediciones obtenidas por distintos evaluadores al aplicar el instrumento a los mismos participantes, y confiabilidad por consistencia interna o correlación entre los distintos ítems o formas paralelas del test (^{Kline, 2015}).

Desde la teoría clásica de test, la validez hace referencia a si un instrumento realmente mide lo que afirma evaluar (^{Moses, 2017}). Tradicionalmente se distinguen tres tipos de validez: de contenido o en qué medida los ítems cubren el dominio de contenido del constructo; de criterio o correlación con otra medida confiable y válida que mide el mismo constructo u otro muy afín, y de constructo o grado en que se confirman las relaciones esperadas bajo la teoría y definiciones que sustentan al constructo. La validez de constructo incluye tanto el contraste del modelo estructural como la aportación acumulativa de evidencias de validez concurrentes, predictivas y retrodictivas (^{Furr, 2017}).

Se considera que, una vez demostrada la validez de contenido, criterial y de constructo, queda establecida la validez de un instrumento de medida (^{Moses, 2017}). Este enfoque tradicional de tres tipos de validez empezó a ser revisado en la década de 1970 (^{Furr, 2017}). Por una parte, Cronbach (1971) enfatizó que las evidencias de validez ofrecen apoyo a las inferencias hechas con un instrumento en un contexto dado, con una muestra dada. Por otra parte, ^{Messick (1975)} concibió la validez como un conjunto de evidencias que ayudan a establecer la relación entre las puntuaciones en un instrumento y el constructo medido, esto es, el grado en que la evidencia y la teoría apoyan las interpretaciones de las puntuaciones en el test desde los usos propuestos para el mismo.

Ambos enfoques desplazaron la atención hacia la aplicación del instrumento en contextos concretos frente al planteamiento inicial más general o universalista, en el cual la confiabilidad y validez una vez probadas ya quedan establecidas. De este nuevo enfoque surge la necesidad de validar y baremar el instrumento de medida en los distintos contextos en que se aplica, como distintos contextos culturales (^{Loewenthal & Lewis, 2018}).

Con el desarrollo del análisis factorial confirmatorio (^{Jöreskog, 1978}; ^{Jöreskog, Olsson, & Wallentin, 2016}), no solo vino una nueva estrategia para aportar evidencias de validez de constructo (^{Bollen, 1989}), sino también nuevas propuestas para el cálculo de la confiabilidad a través de la consistencia interna sin asumir que exista una covarianza homogénea entre las puntuaciones verdaderas y los errores de medida de los ítems (tau-equivalencia). Por ejemplo, se tienen las propuestas de ^{Jöreskog (1971)} y ^{Werts, Rock, Linn y Jöreskog (1978)} sobre el coeficiente de confiabilidad compuesta.

La validez convergente del factor

Al usarse análisis factorial confirmatorio cada factor posee unos indicadores, y se considera como requisito necesario demostrar que los indicadores propuestos miden dicho factor (^{Jöreskog, 1978}). De aquí surge el concepto de la validez convergente de un modelo de medida, cuyo antecedente es la validez a través de matrices de correlación multirasgo-multimétodo introducida por Campbell y Fiske a finales de la década de 1950 (^{Jöreskog et al., 2016}).

¿Qué es la validez convergente de un modelo de medida o factor? Dado un factor con n indicadores o ítems, este tipo de validez hace referencia al grado de certeza que se tiene en que los indicadores propuestos miden una misma variable latente o factor. Al preguntar si un modelo de medida posee validez convergente se pretende averiguar si el constructo es adecuadamente medido por los indicadores propuestos (^{Cheung & Wang, 2017}).

^{Fornell y Larcker (1981)} propusieron la VME calculada desde los pesos de medida estandarizados para evaluar la validez convergente del modelo de medida. Dado un factor o variable latente con k indicadores, la VME^ (ecuación 1) es igual al promedio de los k pesos de medida estandarizados elevados al cuadrado ( λ^i2 ), los cuales son estimados a partir de una muestra de n participantes, usando uno de los métodos desarrollados para modelamiento de ecuaciones estructurales, como máxima verosimilitud o mínimos cuadrados no ponderados (^{Fornell & Larcker, 1981}).

Ecuación 1. Varianza Media Extraída

^{Fornell y Larcker (1981)} fijaron el criterio de que un factor, con independencia de su número de indicadores, debe explicar más del 50 % de la varianza de los mismos para que se pueda considerar que posee validez convergente (nivel aceptable), e indicaron que, de preferencia, debería explicar más del 70 % (nivel bueno). El argumento es que la varianza atribuible al factor sea mayor que la no atribuible.

^{Hair, Black, Babin y Anderson (2010)}, al requisito de una VME mayor que .5, le añadieron pesos de medidas estandarizadas de al menos .5 en todos los indicadores y una confiabilidad compuesta de al menos .7. Tras un estudio de simulación, ^{Cheung y Wang (2017)} también recomendaron una VME no significativamente menor que .50 y unos pesos de medidas estandarizados no significativamente menores que .50 en todos los indicadores.

La confiabilidad compuesta o de constructo

Actualmente, como señalan ^{Green y Yang (2015)}, se recomienda el uso del coeficiente de confiabilidad compuesta ( CR^ ) para evaluar la confiabilidad por consistencia interna (ecuación 2). Este índice también es conocido como coeficiente ρ de ^{Jöreskog (Jöreskog, 1971}, ¹⁹⁷⁸) o coeficiente ω de ^{McDonald (1999)}. Se ideó para modelos de medida congenéricos y así poder superar la limitación del coeficiente alfa de Cronbach que requiere que los ítems sean esencialmente tau-equivalentes (^{Cho & Kim, 2015}).

La varianza verdadera se estima a través del cuadrado de la suma de los pesos de medida estandarizados. Para obtener la varianza del test, a la varianza verdadera se le suma la varianza del error de medida. La varianza del error de medida se calcula por la suma de la varianza de los residuos o suma de cuadrados de los complementos de los pesos de medida estandarizados. El cociente entre la varianza verdadera y la varianza del test proporciona el coeficiente de confiabilidad (^{Green & Yang, 2015}).

Ecuación 2. Confiabilidad compuesta, coeficiente rho o coeficiente omega

Se ha estipulado que valores entre .70 y .79 en el coeficiente omega reflejan niveles de confiabilidad por consistencia interna aceptables al indicar que al menos el 70 % de la varianza de las mediciones o puntuaciones empíricas en el test están sin error. A su vez, unos valores entre .80 y .89 se consideran buenos, y mayores o iguales que .90 se juzgan excelentes (^{Cho & Kim, 2015}; ^{Green & Yang, 2015}; ^{Viladrich, Angulo-Brunet & Doval, 2017}). No obstante, se señala que valores mayores que .94 pueden indicar la presencia de ítems redundantes (^{Kline, 2015}).

Una variante del coeficiente de confiabilidad compuesta es el coeficiente de confiabilidad congenérica ( ρ^c ) de ^{Cho (2016)}. En su fórmula (Ecuación 3), el denominador del coeficiente de confiabilidad es la varianza del test, lo que lo hace que sea un índice más comparable con otros coeficientes de confiabilidad basados en la teoría clásica de test y desarrollados bajo el supuesto de ítems esencialmente tau-equivalentes (^{Cho, 2016}).

Ecuación 3. Del coeficiente de confiabilidad congenérica

Al plantear que los ítems son esencialmente tau-equivalentes se parten de unos supuestos recogidos dentro de la teoría clásica de test o del error de medida (^{Pakzad & Alaeddini, 2017}). Estos supuestos son: 1) la puntuación observada en un ítem es la suma de dos puntuaciones independientes, una puntuación verdadera y un error de medida; 2) la media de los errores de medida del ítem es cero; 3) los errores de medida de dos ítems de la escala son independientes, y 4) las puntuaciones verdaderas de un ítem y el error de medida del otro ítem también son independientes (^{Jabrayilov et al., 2016}).

Bajo estos supuestos, se dice que tres o más ítems son paralelos si sus puntuaciones verdaderas y las varianzas de sus errores de medida son equivalentes; esto implica que las medias, varianzas, covarianzas y correlaciones de las puntuaciones observadas son estadísticamente homogéneas. Tres o más ítems son tau-equivalentes si sus puntuaciones verdaderas son equivalentes, aunque las varianzas de sus errores de medida no lo sean; esto implica que las medias y covarianzas de las puntuaciones observadas son estadísticamente equivalentes, pero las varianzas y correlaciones pueden ser heterogéneas. Tres o más ítems son esencialmente tau-equivalentes si sus puntuaciones verdaderas son combinación lineal unas de otras bajo operaciones de adición o sustracción, aunque las varianzas de sus errores sean heterogéneas; esto implica que las covarianzas entre las puntuaciones observadas son estadísticamente homogéneas, aunque las medias, varianzas y correlaciones de las puntuaciones observadas pueden ser heterogéneas (^{Jabrayilov et al., 2016}; ^{Pakzad & Alaeddini, 2017}).

Entre las nuevas técnicas para evaluar la confiabilidad por consistencia interna, también se tiene el coeficiente H de ^{Hancock y Müeller (2001)} o confiabilidad de la combinación lineal óptima entre ítems (Ecuación 4). Este coeficiente se propone como una estimación del límite superior de la confiabilidad por consistencia interna de un test sin requerir el supuesto de tau-equivalencia (^{Domínguez-Lara, 2016}), como el coeficiente ω que se basa en los pesos de medida estandarizados, además, no requiere que los ítems estén puntuados en el mismo sentido, como sí ocurre con el coeficiente α y el coeficiente ω al estar los pesos de medida elevados al cuadrado (^{McNeish, 2018}). Se requiere un valor de al menos .70 para reflejar confiabilidad (^{Domínguez-Lara, 2016}; ^{Hancock & Müeller, 2001}).

Ecuación 4. Coeficiente de confiabilidad H

Diferencia y semejanza entre validez convergente y confiabilidad de constructo

La diferencia entre ambos conceptos radica en que la validez convergente intenta estimar en qué proporción la varianza de los indicadores de un factor es explicada por una fuente atribuible (el factor) y no por fuentes no atribuibles (los errores). La confiabilidad compuesta o de constructo pretende separar la varianza del factor medida sin error (varianza verdadera) y con error (varianza del error de medida). La varianza del test es la suma de la varianza verdadera y la del error de medida. En un principio son dos conceptos próximos o afines, pero claramente distinguibles.

La semejanza fuerte aparece cuando las estimaciones se hacen desde los pesos de medidas estandarizados que el factor tiene sobre los ítems bajo el supuesto de que los errores de medidas son independientes (Figura 1). La varianza verdadera se obtiene al sumar los pesos de medida y elevar esta suma al cuadrado. La varianza del error de medida se obtiene al sumar los complementos de la varianza explicada por el factor en cada ítem. Esta varianza explicada es el peso de medida elevado al cuadrado. El promedio de estos pesos al cuadrado proporciona la varianza atribuible al factor y su complemento, la varianza no atribuible. En este punto, la semejanza los hace muy parecidos y complementarios, como ya lo reconocen investigadores como ^{Green y Yang (2015)}, ^{Hair et al. (2010)} y ^{Rodríguez, Reise y Haviland (2016)}.

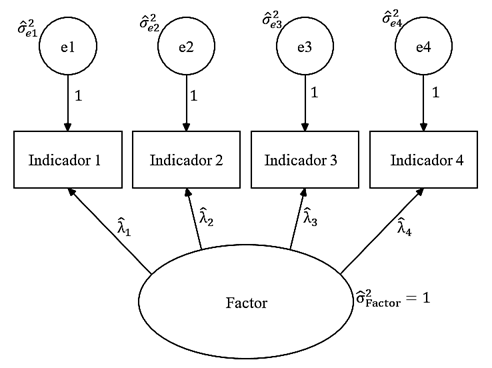
Figura 1 Modelo de un factor con dos grados de libertad o diferencia entre los 10 momentos muestrales (seis covarianzas y cuatro varianzas) y los ocho parámetros a estimar (las cuatro varianzas de residuos de medida y los cuatro pesos de medida tras fijar a un valor unitario la varianza del factor y los pesos de los residuos). 

Se podría decir que ambos conceptos pretenden estimar una varianza atribuible a un modelo de medida especificado con k indicadores. Dicho en otras palabras, ambos conceptos plantean responder a la pregunta de si el modelo de medida de un constructo posee una variabilidad compartida o varianza verdadera (sin error) suficiente para ser una buena medición. Desde esta similitud se podría reconsiderar el valor crítico para la VME desde los valores críticos propuestos para el coeficiente de confiabilidad compuesta (coeficiente ω) y de constructo (coeficiente H).

A parir de lo previamente argumentado se plantea un estudio metodológico que tiene como objetivo revisar el punto de corte estipulado para la VME cuando se usa para establecer la validez convergente de un modelo de medida.

Valores del peso de medida estandarizado homogéneo para alcanzar valores mínimos de confiabilidad aceptable, buena o excelente variando el número de indicadores del factor

¿Qué peso medida estandarizado se requeriría para alcanzar valores de .70, .80 y .90 en los coeficientes ω y H? Considerando la correlación entre el ítem y el factor o peso de medida estandarizado constante, se tendría para el coeficiente ω de ^{McDonald (1999)}:

Ecuación 6. Peso de medida homogéneo ante un valor dado de confiabilidad compuesta

Por ejemplo, para tres indicadores, k = 3 (Tabla 1), aplicando las ecuaciones 6 y 5:

Por ejemplo, para cuatro indicadores, k = 4 (Tabla 1), aplicando las ecuaciones 6 y 5:

Por ejemplo, para cinco indicadores, k = 5 (Tabla 1), aplicando las ecuaciones 6 y 5:

Con el coeficiente H de ^{Hancock y Müeller (2001)} resultaría igual:

Ecuación 7. Peso de medida homogéneo ante un valor dado del coeficiente H

Relación entre el número de indicadores del factor y la validez convergente

Desde los datos de la Tabla 1 se obtiene una correlación negativa entre el número de indicadores del factor (k) y el valor del indicador de validez convergente ( VME^ ). La fuerza de asociación de estas correlaciones varía de muy grande a perfecta. Cuando ω^ = H^ = .70, la correlación entre k y VME^ es de -.89 (varianza compartida del 79.1 %). Cuando ω^ = H^ = .80, la correlación entre k y VME^ es de -.91 (varianza compartida del 83.6 %). Cuando ω^ = H^ = .90, la correlación entre k y VME^ es de -.95 (varianza compartida del 90.5 %). Consecuentemente, al incrementar el número de indicadores y mantener constante la confiabilidad, el valor de VME^ decae bajo una relación lineal casi perfecta. Al comparar estos coeficientes de correlación por la prueba Z de Steiger, esta fuerza de asociación es significativamente más grande (más negativa) a medida que mejora el nivel de confiabilidad: Z = 4.60, p < .001 al comparar los valores de VME^ entre la primera y segunda condición de confiabilidad; Z = 4.91, p < .001 al comparar los valores de VME^ entre la primera y la tercera condición de confiabilidad; así como Z = 4.84, p < .001 al comparar los valores de VME^ entre la segunda y la tercera. Por tanto, el decremento del valor de VME^ con el incremento de indicadores empeora al ser mayor el nivel de confiabilidad.

Valores del coeficiente ω y H ante pesos de medida estandarizados homogéneos de .50, .71 y .84 variando el número de indicadores del factor

Al mantener constantes las correlaciones homogéneas entre los ítems y el factor se puede observar que los coeficientes ω^ y H^ son más altos cuanto mayor es el número de indicadores (Tabla 2). Por ejemplo, con un peso de medida estandarizado de .50, el cual es considerado alto en el análisis factorial (^{Bollen, 1989}; ^{Hair et al, 2010}; ^{Wu & Leung, 2017}), pero que proporciona una VME insuficiente, VME^ = .25 (^{Fornell & Larcker, 1981}), la confiabilidad con seis indicadores sería cuestionable, ω^ = H^ = .67 < .70 (^{Hancock & Müeller, 2001}; ^{McDonald, 1999}); pero con siete indicadores sube a aceptable, ω^ = H^ = .70, con 12 indicadores a buena, ω^ = H^ = .80 y con 26 indicadores a excelente, ω^ = H^ = .90 (Tabla 2).

El número mínimo de indicadores para un factor considerado como admisible es tres en el caso de un modelo de dos o más factores (^{Jöreskog et al., 2016}). Ante un modelo de un factor se requieren cuatro indicadores para que el modelo esté sobreidentificado y permita no solo estimar los parámetros, sino también contrastar el ajuste a los datos (Figura 1). Con tres indicadores con pesos de medida de .66, se logra que los coeficientes ω^ y H^ tomen un valor de .70, lo que implica una VME^ de .44. Con pesos de medida de .71 se logra una VME^ de .50 y los coeficientes ω^ y H^ serían de .75, lo que corresponde a un valor de consistencia interna también aceptable. Con pesos de .76 y una VME^ de .57, ambos coeficientes subirían a un valor de consistencia interna bueno, ω^ = H^ = .80 (Tabla 2).

Entre cuatro y cinco se considera un número medio de indicadores y seis o más, alto (^{Perry, Nicholls, Clough & Crust, 2015}). Con cuatro indicadores con pesos de medida de .61 se logra que los coeficientes ω y H tomen un valor de .70, lo que implica una VME^ de .37; con pesos de medida de .71 y VME^ de .50 y los coeficientes ω^ y H^ sería de .80, lo que corresponde a un valor de consistencia interna bueno. Con cinco indicadores con pesos de medida de .56, se logra que los coeficientes ω y H tomen un valor de .70, lo que implica una VME de .32; con pesos de medida de .71 y VME^ de .50 y los coeficientes ω^ y H^ sería de .83, lo que corresponde a un valor de consistencia interna bueno. Con seis indicadores con pesos de medida de .53 se logra que los coeficientes ω y H tomen un valor de .70, lo que implica una VME de .28; con pesos de medida de .71 y AVE^ de .50 y los coeficientes ω^ y H^ sería de .86, lo que corresponde a un valor de consistencia interna bueno. Con siete indicadores con pesos de medida de .50 se logra que los coeficientes ω y H tomen un valor de .70, lo que implica una VME de .25; con pesos de medida de .71 y AVE^ de .50 y los coeficientes ω^ y H^ sería de .88, lo que corresponde a un valor de consistencia interna bueno (Tabla 2).

Más de 20 ítems se suelen considerar un número excesivo de indicadores para un factor (^{Van der Eijk & Rose, 2015}). Con 21 indicadores o más con cargas menores que .60 y valores de VME^ menores o iguales que .30, se logran valores de consistencia interna excelentes ( ω^ y H^ ≥ .90) (Tabla 2).

Relación entre el número de indicadores del factor y la confiabilidad

Desde los datos de la Tabla 2 se obtiene una correlación positiva entre el número de indicadores y el valor del coeficiente de confiabilidad. La fuerza de asociación de estas correlaciones varía de muy grande a perfecta. Cuando VME^ = .25, la correlación entre k y los coeficientes ω^ o H^ es de .90 (varianza compartida del 81.1 %). Cuando VME^ = .50, la correlación entre k y los coeficientes ω^ o H^ es de .86 (varianza compartida del 73.8 %). Cuando VME^ = .70, la correlación entre k y los coeficientes ω^ o H^ es de .84 (varianza compartida del 70.5 %). Al incrementar el número de indicadores y mantener constante el nivel de validez convergente, el coeficiente de confiabilidad se incrementa bajo una relación lineal casi perfecta. Al comparar estos coeficientes de correlación por la prueba Z de Steiger, esta fuerza de asociación fue significativamente menor a medida que mejora el nivel de validez convergente: Z = 4.37, p < .001 al comparar los valores de los coeficientes ω^ o H^ entre la primera y segunda condición de validez convergente, Z = 4.48, p < .001 al comparar los valores de los coeficientes ω^ o H^ entre la primera y la tercera condición de validez convergente, así como Z = 4.24, p < .001 al comparar los valores de los coeficientes ω^ o H^ entre la segunda y la tercera. Por tanto, el incremento de la confiabilidad con el incremento de indicadores es menor al ser mayor el nivel de validez convergente.