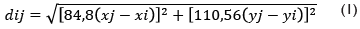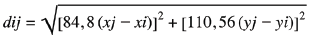Introducción
En un problema de enrutamiento de vehículos VRP (vehicle routing problem) se pretende diseñar las rutas de una flota de transporte que sirve a un conjunto de clientes. Cada vehículo parte de un depósito principal, recorre un determinado número de clientes, y finalmente vuelve al depósito principal (ciclo hamiltoneano). Los clientes o nodos deben ser visitados una única vez por un único vehículo, y la demanda agregada de todos los nodos asignados a un vehículo no debe superar su capacidad. Un problema de enrutamiento abierto de vehículos OVRP (open vehicle routing problem) es una variante trivial del clásico VRP, que difiere en que, una vez cada vehículo sirve a todos y cada uno de los nodos que le han sido asignados, no está obligado a volver al depósito (camino hamiltoneano). En otras palabras, cada ruta en el OVRP parte desde el depósito inicial, y termina necesariamente en un cliente. Desde esta perspectiva, el OVRP cuenta con un gran atractivo para organizaciones que optan por subcontratar una flota de vehículos en lugar de adquirir una propia. (Sariklis and Powell, 2000; Tarantilis, et al. 2005; Repoussis, et al. 2007).
En la institución prestadora de salud (IPS), donde se desarrolló el presente estudio, se brinda atención a pacientes no crónicos, que por su condición de discapacidad mental y movilidad reducida deben ser trasladados desde sus lugares de residencia hasta la sede principal de la IPS, para recibir la asistencia médica que necesitan. El diseño de las rutas, y la consecuente asignación de los pacientes a cada una de ellas, obedece a un criterio netamente empírico que realiza un profesional de salud funcionario de la IPS que no cuenta con los conocimientos y las técnicas de optimización logística. Como consecuencia, durante la operación del sistema los vehículos se ven envueltos en atascamientos innecesarios de tránsito, demoras y tiempos y distancias recorridas por encima de lo previsto, y que afectan, no solo a los pacientes transportados, sino los costos finales de todo el sistema.
Por lo anterior esta investigación tiene como objetivo proponer un diseño de rutas y asignación de pasajeros que reduzca los costos de prestación de servicios para una Institución Prestadora de Servicios de Salud (IPS)
1. Marco teórico
El VRP fue introducido por primera vez en los años cincuenta y sesenta por Dantzig, et al. (1954), Dantzig, et al. (1959), y Clarke and Wright (1964), mientras que el OVRP, fue desarrollado de la mano de Schrage (1981), mucho después. En esa oportunidad solo se propuso el problema, pero no se le dio nombre ni formulación formal ni propuesta de solución. Poco más tarde, Raff (1983) presentaría la primera solución a un problema de éste tipo.
Seguirían algunos trabajos, como los de Fu and Wright (1994), Ben Atkinson (1990), y Li and Fu (2002), antes de que Sariklis and Powell (2000) hiciera su formulación formal y le otorgara el nombre con el que hoy se conoce. Con la llegada del nuevo milenio, y con el auge que la tercerización de servicios ha experimentado en los últimos años, el OVRP ha dejado de ser tímidamente abordado y ha cobrado gran relevancia. Esto debido a que cada vez más empresas optan por subcontratar el servicio de transporte en vez de adquirir una flota propia para tal fin. Por lo anterior, el OVRP se clasifica en la categoría de problemas de logística de terceros o 3PL (third party logistics), de acuerdo a autores como Hedar and Abdallah (2014); Repoussis, et al. (2007); Russell, et al. (2008) y Tarantilis, et al. (2005)
Además de desarrollar un modelo de optimización de rutas de una situación de la vida real, nuestro interés en el OVRP es motivado por su importancia práctica y teórica. En el plano práctico y desde una perspectiva comercial, numerosas actividades de distribución en el mundo real encajan en el marco del OVRP, por ejemplo, la distribución tercerizada de paquetes y/o mercancías, o el transporte de pasajeros como el caso del reparto de estudiantes al final de la jornada escolar. En la bibliografía disponible, se pudieron encontrar algunas aplicaciones reales. Por ejemplo, el reparto de periódicos (Russell, 2013; Russell, et al. 2008; Sevkli and Güler, 2017), la generación de rutas de entrega con flota de aviones (Raff, 1983), el transporte ferroviario de mercancías (Fu and Wright, 1994), la distribución de productos lubricantes (Repoussis, et al. 2009b), el transporte de material en una mina de carbón (Guo and Yu, 2012; Yu, et al. 2011), el transporte escolar (López-Sánchez, et al. 2014; GurpreetS-ingh and Dhir, 2014; Özyurt, et al. 2006; Bektas and Elmas-tas, 2007), la entrega de comidas escolares (Ben Atkinson, 1990), la distribución de los cables en parques eólicos marinos (Bauer and Lysgaard, 2015), el sistema de transporte de un centro de distribución a supermercados (Tarantilis, et al. 2005), el transporte de pasajeros en buses intermunicipales (Scárdua, et al. 2016), entre otros.
La importancia teórica del OVRP radica en que es un problema de optimización combinatoria del tipo NP-hard. Resolver el OVRP, esto es: encontrar una solución pseudo-óptima en un tiempo de computo máximo preestablecido, implica construir el mejor camino hamiltoneano para cada grupo de clientes asignado a un vehículo. Como dicha asignación es de naturaleza combinatoria NP-Hard, el OVRP también lo es (Syslo, et al. 1983). Un modelo de programación entera del OVRP se puede consultar en los trabajos de Sevkli and Güler (2017); Shamshirband, et al. (2015); MirHassani and Abolghasemi (2011).
Para intentar dar solución al OVRP se han implementado distintas técnicas heurísticas a lo largo de los años. Las heurísticas buscan de manera aleatoria (estadística) e iterativa, encontrar soluciones pseudo óptimas dentro del conjunto de puntos del espacio muestral. Una solución pseudo óptima es la que, sin garantía de ser el óptimo global, mejora las soluciones actuales, normalmente empíricas, y a veces construidas por prueba y error en la vida real. Dentro de las que han sido usadas para dar solución al OVRP podemos resaltar: branch-and-cut (Pessoa, et al. 2008; Letchford, et al. 2007), voraz (Yilmaz, et al. 2014; Repoussis, et al. 2007; Ben Atkinson, 1990), Clark and Wright (Pichpibul and Kawtum-machai, 2013; Özyurt, et al. 2006), agrupar primero rutear después (Sariklis and Powell, 2000), programación lineal entera ILP (Salari, et al. 2010), búsqueda en vecindario variable . VNS y sus variantes (Subramanian, et al. 2013; Reinholz and Schneider, 2013; Redi, et al. 2013; Penna, et al. 2012; Sevkli and Güler, 2017; Kritzinger, et al. 2016), búsqueda local LS y sus variaciones (Schopka and Kopfer, 2016; Soto, et al. 2017; Chen, et al. 2016; Yilmaz, et al. 2014; Zachariadis and Kiranoudis, 2010), búsqueda amplia (Pisinger and Ropke, 2007), generación por columnas (Yousefikhoshbakht and Dolatnejad, 2017; Yousefikhoshbakht, et al. 2016), hiper-heurísticas (Tyasnurita, et al. 2017), entre otros.
Un papel preponderante, dentro del conjunto de técnicas implementadas para dar solución al OVRP, ha sido el de los métodos metaheurísticos. Estos métodos, como los heurísticos, buscan de manera iterativa soluciones pseudo-óptimas, pero a diferencia de ellos, sus algoritmos están inspirados y construidos para imitar un patrón de comportamiento o ciertos fenómenos de la naturaleza. Dentro de los que se han construido para tal fin se encuentra la búsqueda tabú (Russell, 2013; Wang, et al. 2012; Li, et al. 2012; Jinhui, et al. 2012; Yu, et al. 2011; Derigs and Reuter, 2009; Hedar and Abdallah, 2014), el recocido simulado (Vincent, et al. 2016; Ge, et al. 2010; Li, et al. 2007), el algoritmo genético (Wang, et al. 2015; Liu, et al. 2014b,a; Yilmaz, et al. 2014; Cao, et al. 2014; Guo and Yu, 2012; Ren, 2011; Yang and Zhao, 2010), la optimización por colonia de hormigas (Yousefikhoshbakht, et al.2015; Sedighpour, et al. 2014; GurpreetSingh and Dhir, 2014; Ashouri and Yousefikhoshbakht, 2017; Ge, et al. 2016), la optimización por cúmulo de partículas (Naderipour and Alinaghian, 2016; Norouzi, et al. 2012; MirHassani and Abolghasemi, 2011; Hu and Wu, 2010), el algoritmo de selección clonal (Pan and Fu, 2009), el algoritmo de búsqueda gravitacional (Hosseinabadi, et al.2016a,b), el algoritmo de optimización por apareamiento de abejorros (Marinakis and Marinaki, 2011a,b), el algoritmo memético (Repoussis. et al. 2010; Labadie, et al. 2016), algoritmo del imperialista competitivo (Shamshirband, et al. 2015; Yousefikhoshbakht, et al. 2012), el algoritmo evolutivo (Zhao, et al. 2010; Repoussis, et al. 2010; Cao and Lai, 2010; Zhang, et al. 2009), entre otros.
Aunque en la mayoría de los algoritmos implementados intentan minimizar los costos de operación y el número de vehículos empleados, es posible encontrar algunos trabajos cuyos objetivos pretenden minimizar otras variables, como el tiempo de recorrido (Li and Fu, 2002), la distancia recorrida (Shamshirband, et al. 2015; Marinakis and Marinaki, 2011a), el número de vehículos de la flota (Hosseinabadi, et al. 2016b; Chen, et al. 2016; Hosseinabadi, et al. 2016a; Marinakis and Marinaki, 2011b), el tiempo que invierte el vehículo en una persona (Wang, et al.2015), la cantidad de emisiones de gases de efecto invernadero (Naderipour and Alinaghian, 2016), el uso de los vehículos (Lalla-Ruiz, et al. 2016; Lalla-Ruiz and Voß, 2016), entre otros.
Cuando se añade una restricción de capacidad a los vehículos los autores prefieren llamar a este problema: capacitated open vehicle routing problem -COVRP- (Fu, 2004; Letchford, et al. 2007; Pessoa, et al. 2008). Esta no es la única variante del OVRP. Existen, en la literatura disponible, algunas otras que podemos mencionar: multidepósito -MDOVRP- (Soto, et al 2017; Lalla-Ruiz, et al. 2016; Liu, et al. 2014b,a; Lalla-Ruiz and Voß, 2016), con cross-docking -OVRPCD- (Vincent, et al. 2016), con flota heterogénea fija -HFFOVRP- (Ruiz, et al. 2016; Yousefikhoshbakht, et al. 2015; Penna, et al. 2012; Li, et al. 2012; Ren, 20ll;Yousefikhoshbakht and Dolatnejad, 2017; Yousefikhoshbakht, et al. 2016), limitado a ventanas de tiempo -OVRPTW- (Redi, et al. 2013; Repoussis, et al. 2009a, 2007), limitado a ventanas suaves de tiempo -OVRPSTW-(Jinhui, et al. 2012; Fenghua and Xiaonian, 2008), limitado a ventanas rígidas de tiempo -OVRPHTW- (Wang, et al. 2012), robusto o con demanda incierta -ROVRP, (Cao, et al. 2014), con demanda difusa -OVRPFD- (Cao and Lai, 2010), con restricciones de zona -OVRPZC- (Russell, et al. 2008), con nodos de cierre o homedepots -OVRP-d- (Aksen, et al. 2007) , con tiempo máximo de entrega -OVRPTD- (Aksen, et al. 2007; Özyurt, et al. 2006), para varias empresas aliadas -MEAOVRP- (Yang and Zhao, 2010), con competencia entre distribuidores -OVRPCTW- (Norouzi, et al. 2012), con entrega dividida -SDOVRP- (Chen, et al. 2016), multiproducto -OVRPMP- (Yilmaz, et al. 2014; Russell, et al. 2008) , planar -POVRP- (Bauer and Lysgaard, 2015), invertido -ROVRP- (Schopka and Kopfer, 2016), dependiente del tiempo -OTDVRP- (Naderipour and Alinaghian, 2016), balanceado -BOVRP- (López-Sánchez, et al. 2014), con recogidas y entregas -OVRPPD- (Ben Atkinson, 1990; Tambunan and Mawengkang, 2015), con puntos de reclamo -OVRPDP-(Atefi, et al. 2018), y mezclas entre ellos (Schopka and Kopfer, 2016;Wang, et al. 2015;Yilmaz, et al 2014; Norouzi, et al. 2012; Tambunan and Mawengkang, 2015).
2. Metodología
El enfoque metodológico seleccionado para el desarrollo de esta investigación es cuantitativo soportado en la aplicación de técnicas de la investigación de operaciones para la construcción de un modelo de optimización de enrutamiento abierto de vehículos con restricción de capacidad COVRP de una Institución Prestadora de Servicios de Salud IPS de la ciudad de Barranquilla (Colombia), haciendo uso de dos heurísticos: algoritmo del vecino más cercano NN (por sus siglas en inglés Nearest Neighbour Algorithm), y algoritmo modificado del vecino más cercano, con el objetivo de encontrar la mejor solución. Cuando decimos «solución» hacemos referencia a la asignación recursiva de los nodos a las rutas, de tal manera que se logre la utilización mínima de vehículos a la vez que se logra la disminución de los costos de transporte.
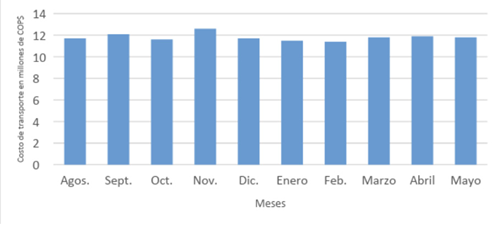
Durante el periodo comprendido entre agosto 2016 y mayo 2017, la IPS en cuestión ha experimentado un aumento en el costo de transporte como se muestra en la Figura 1. Ello se debe, no solo al aumento de la cobertura hospitalaria, sino, a un enrutamiento ineficiente de los nuevos clientes. Por lo anterior, se requiere entonces de un diseño de rutas y asignación de pasajeros con un criterio científico que reduzca los costos de prestación de servicios, optimice los tiempos de transporte y minimice el número de vehículos, así como la utilización de sus capacidades. Por sus características y restricciones, esta situación de la vida real encaja en el modelo del OVRP con restricción de capacidad.
Los algoritmos que se emplearon para dar solución al problema propuesto hacen uso de la estructura de costos de la operación de los vehículos que componen la flota empleada, y de las distancias entre todos y cada uno de los nodos (pacientes) del problema. Una vez obtenidos estos parámetros se construyeron tres algoritmos: el de la distancia euclidiana entre nodos, el del vecino más cercano (NN), y el modificado del vecino más cercano (NN modificado). A continuación, se presentan las estructuras de los algoritmos.
2.1. Estructura de costos
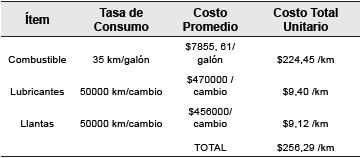
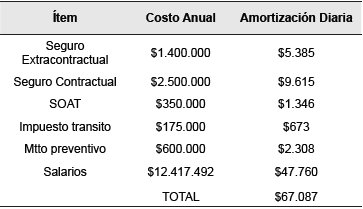
Con el propósito de obtener los costos asociados al problema, se consultó la estructura de costos de la flota empleada. Los costos variables obedecen, básicamente, al consumo de combustible, el uso del aceite del motor y su filtro, el aceite de la caja de cambios, y el desgaste de los neumáticos. Los costos fijos obedecen al salario del conductor, a los servicios de aseo y limpieza, y a la amortización diaria de los seguros e impuestos anuales del vehículo. Los costos se calcularon con base en un vehículo camioneta tipo van, con capacidad para catorce pasajeros (Q = 14, marca CHANGAN, de referencia STAR7, modelo 2017 y de fabricación china). En las Tablas 1 y 2, se presenta el desglose de los costos variables y fijos, respectivamente. En ellas se observa un costo variable por kilómetro cv =$256,29 y un costo fijo por vehículo cf = $67 087.
La reducción porcentual se estimará comparando los costos estimados con cada heurística (cvΣdk +kcf, donde dk es la distancia total recorrida de la k-ésima ruta, y K es número total de rutas programadas), con el costo promedio diario en transporte de los últimos diez meses en la organización y que asciende a $418 451.
2.2. Matriz de distancias
Para obtener la distancia dij entre cada uno de los nodos se hizo uso de la ecuación (1) que es la aproximación que propone el SIAMAC (Centro de Información de la Amazonía Colombiana) para obtener la distancia euclidiana entre dos coordenadas geográficas geodésicas en el sistema WGS84 (SIAMAC and Universidad Nacional de Colombia Sede Amazonía, 2010).
El suministro de las direcciones de los domicilios de los pacientes por parte de la IPS, permitió el uso del Sistema de Información Geográfica Google Maps. Esta información se utilizó para obtener la matriz con las coordenadas geográficas geodésicas en el sistema WGS84 de todos los nodos
Donde (xi; yi) y (xj; yj) son las coordenadas geodésicas del nodo i y del nodo j, respectivamente; di j esta dado en km. La matriz de distancias D se obtuvo con el Algoritmo 1.
2.3. Algoritmo del vecino más cercano
La técnica NN es una heurística de inserción secuencial. Las heurísticas de inserción son métodos constructivos en los cuales se crea una solución mediante sucesivas inserciones de nodos (viviendas) en las rutas. En cada iteración se tiene una solución parcial cuyas rutas sólo visitan un subconjunto de los clientes y se selecciona un cliente no visitado para insertar en dicha solución. En las heurísticas de inserción secuencial sólo se considera insertar clientes en la última ruta creada. El algoritmo de vecino más cercano genera rutas uniendo vértices, puntos o nodos, teniendo en cuenta la arista con la menor distancia o costo de un punto al resto de puntos.
Algoritmo 2. NN para el COVRP
Entrada: D; qi, la demanda del i-ésimo nodo; Q.
Salida: R, la matriz de rutas; costos totales
C = cvD.
Costos actuales acumulados ← 0.
Activar la primera ruta en R.
Ocupación de la primera ruta ← 0.
Nodo actual ← Depósito.
while Nodos asignados ≤ Total de nodos do
En el renglón del nodo actual, buscar la distancia más corta en la j-ésima columna de D.
En el renglón del nodo actual, buscar el costo de ir desde el renglón del nodo actual hasta la j-ésima columna de C.
if Ocupación de la ruta actual + qj > Q then
Activar una nueva ruta en R.
Ocupación de la nueva ruta ← 0.
Nodo actual Depósito.
end if
Asigne el j-ésimo nodo a la ruta actual.
Sumar qj a la ocupación de la ruta actual.
Eliminar la j-ésima columna de D.
Sumar el costo de ir al nodo actual a los costos actuales acumulados.
Nodo actual ← j.
end while
Costos fijos totales ← cf x número de rutas en R.
2.4. Algoritmo modificado del vecino más cercano
Este algoritmo resulta de la modificación propuesta en Eppen (2000) para la matriz de distancias D, una vez se obtiene esta matriz, se encuentra el valor máximo por columna. Luego se obtiene la matriz de distancias modificada D*
Con esta modificación es alimentado el algoritmo 2 haciendo un cambio en las líneas 7 y 16 se debe reemplazar D por D*.
3. Resultados
Los algoritmos se programaron en un script .m y se corrieron en el software GNU Octave v4.2.1 en un computador con procesador Intel Core i3-2330, con 6Gb de memoria RAM, y con ArchLinux-Openbox como sistema operativo.
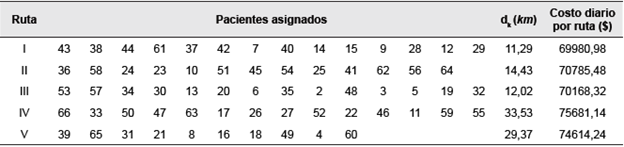
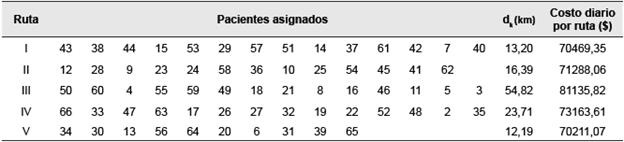
La Tabla 3 muestra la propuesta de enrutamiento haciendo uso de la heurística NN, mientras que la Tabla 4 muestra las rutas con base en la heurística NN modificada. Como se espera en toda heurística voraz, a las primeras rutas se les ha asignado los nodos más cercanos, mientras que los nodos más lejanos han sido asignados en las últimas iteraciones. Es por ello que no existe una distribución equitativa de las rutas por lo que las primeras rutas recorran mucha menos distancia en mucho menos tiempo.
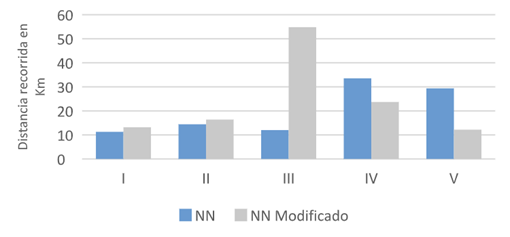
La Figura 2 hace una comparación de las heurísticas en cuanto a la distancia recorrida de cada ruta. En ella se observa una diferencia sustancial en la ruta número 3; en menor proporción, la de las rutas 4 y 5, por último, en un rango más pequeño se encuentran en las rutas 1 y 2. Pese a que se espera que las últimas rutas sean más costosas que las primeras, la ruta 3 para el algoritmo NN y la ruta 4 para el NN modificado rompen el sentido común. Dichas rutas presentan una disminución en la distancia recorrida total frente a la inmediatamente anterior enrutada. Esto puede deberse a la naturaleza misma del problema particular, ya que en esas rutas se asignaron los nodos con mayor número de pacientes, evitando así recorridos adicionales en las rutas posteriores. Como también se esperaba, la última ruta construida presenta un costo inferior a las anteriores en ambas heurísticas porque es la que menor número de pasajeros ocupa.
Los costos totales, los tiempos de cómputo y la reducción relativa que se obtuvo con cada heurística, se muestran en la Tabla 5. Aquí se observa un costo inferior con el programa propuesto por la heurística NN, frente al de la heurística NN modificada. Sin embargo, ésta última presenta un tiempo de cómputo inferior.
4. Conclusiones
En este trabajo se presenta como solución a un problema de enrutamiento abierto de vehículos de la vida real, transporte de pacientes de una institución prestadora de salud (IPS), una propuesta de recorridos obtenida con dos técnicas voraces para la flota que se dispone: heurística del vecino más cercano y heurística del vecino más cercano modificado teniendo en cuenta que el enrutamiento se ajustaba a un OVRP con restricción de capacidad. Se presentaron sus algoritmos, así como la estructura de costos del problema real. Se obtuvieron dos soluciones pseudo óptimas, una por cada heurística. La obtenida por el algoritmo NN fue la solución que presentó una reducción de costos mayor frente a la obtenida con el modificado.
Los algoritmos desarrollados funcionan muy bien con los datos suministrados lográndose una disminución de los costos totales de transporte, ofreciendo una muy buena solución con un mínimo esfuerzo computacional, por lo que esta investigación es una herramienta práctica para la toma de decisiones en lo que respecta al enrutamiento diario de los vehículos que brindan el servicio a la institución prestadora de salud (IPS).
Se recomienda para futuros trabajos la implementación de otros algoritmos heurísticos de construcción para posibilitar una reducción mayor en los costos, las distancias recorridas, y el número de vehículos de la flota.