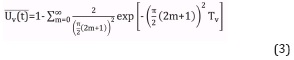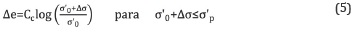Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Científica General José María Córdova
Print version ISSN 1900-6586
Rev. Cient. Gen. José María Córdova vol.10 no.10 Bogotá Jan. 2012
Marco conceptual para el diseño de una herramienta de simulación por computador aplicada a la enseñanza de mecánica de suelos en ingeniería civil*
A Conceptual Framework for Designing a Computer Simulation Tool Applied to the Teaching of Soil Mechanics in Civil Engineering
Un cadre conceptuel pour le développement d'un outil de simulation informatique appliqué à l'enseignement de la mécanique des sols en l'ingénierie civile
Marco conceitual para o desenho de uma ferramenta de simulação por computador aplicada ao ensino de mecânica dos solos em Engenharia Civil
Javier Fernando Camacho-Tautaa
Orlando Germán Posso-Arévalob
* Artículo de investigación exploratoria asociado al proyecto "Simulación por computador como alternativa para la enseñanza de laboratorios en ingeniería civil" (Código: FING-00512) financiado por la Escuela Militar de Cadetes "General José María Córdova". Investigador Principal: Javier Fernando Camacho Tauta. Coinvestigador: Orlando Germán Posso.
a Ingeniero Civil de la Unicersidad Militar Nueva Granada, Magister en Ingeniería Civil de la Universidad de los Andes, Doctor en Ingeniería Civil de la Universidad Técnica de Lisboa. Coordinador de Investigaciones Facultad de Ingeniería Civil de la Escuela Militar de Cadetes "General José María Córdova", Bogotá, Colombia. Comentarios a: jcamachotauta@gmail.com
b Ingeniero Civil de la Universidad Militar Nueva Granada, Especialista en Docencia en la Universidad Militar Nueva Granada, Bogotá, Colombia. Especialista en Gerencia Integral de Obras en la Escuela de Ingenieros Militares. Actualmente es estudiante de Maestría en Educación en la Universidad Militar Nueva Granada. Comentarios a: orlaposso@yahoo.com
Recibido: 10 de Abril de 2012. • Aceptado: 05 de Mayo de 2012.
Resumen
El advenimiento de los computadores ha permitido innovar en estrategias de aprendizaje en variados campos del conocimiento. La simulación por computador es una de estas estrategias, especialmente útil en aquellas áreas en que a diferencia de la experiencia directa en campo o laboratorio, implica menor costo, reducción de la exposición a riesgos físicos o ahorro de tiempo. Una herramienta de simulación por computador debe obedecer a parámetros mínimos de diseño para que pueda favorecer el cumplimiento de los objetivos pedagógicos propuestos. El presente artículo presenta el marco conceptual necesario para el adecuado diseño de una herramienta de simulación por computador y se desarrollan los elementos constitutivos de un modelo matemático utilizado para reproducir el comportamiento físico-mecánico de una masa de suelo aplicable al contexto de la ingeniería civil.
Palabras clave: Simulación por computador, auto-aprendizaje, modelo científico, mecánica de suelos, ingeniería civil.
Abstract
The advent of computers allowed innovation in learning strategies in different fields of knowledge. Computer simulation is one of these strategies, especially useful in areas in which, as opposed to direct experience in field or laboratory, means lower cost, reduction of physical risk or time savings. A computer simulation tool must meet the minimum design parameters that would facilitate the compliance with the proposed educational objectives. This paper presents the conceptual framework necessary for the proper design of a computer simulation tool, and develops the elements of a mathematical model used to reproduce the physical-mechanical behavior of a soil mass applicable to the civil engineering context.
Keywords: Computer simulation, self-learning, scientific model, soil mechanics, civil engineering.
Résumé
L'arrivée des ordinateurs a permis l'innovation technologique dans les stratégies d'apprentissage en divers domaines de la connaissance. La simulation informatique est une de ces stratégies, particulièrement utile pour les domaines dans lesquels, par opposition à une expérience directe dans le champ ou en laboratoire, ce qui signifie moins de coûts en termes de contribuer à diminuer l'exposition aux risques physiques ou economiser du temps. La création d'un outil de simulation informatique doit identifier les paramètres minimaux nécessaires pour veiller à l'application des objectifs pédagogiques. Cet article présente un cadre conceptuel pour le développement d'un outil de simulation sur ordinateur, et prévoit les éléments constitutifs d'un modèle mathématique utilisé pour reproduire le comportement physico-mécanique des sols traités, particulièrement applicable en ingénierie civile.
Mots-clés: Simulation par ordinateur, l'auto-apprentissage, modèle scientifique, mécanique des sols, ingénierie civile.
Resumo
O advento dos computadores tem permitido inovação em estratégias de aprendizagem em diversas áreas do conhecimento. A simulação em computador é uma dessas estratégias, especialmente útil em áreas onde a diferença da experiência direta no campo ou em laboratório significa menor custo, menor exposição a riscos físicos ou economia de tempo. A ferramenta de simulação de computador deve obedecer a parâmetros de projeto mínimos que facilitem o cumprimento dos objetivos educacionais propostos. Este artigo apresenta o marco conceitual necessário para a boa concepção de uma ferramenta de simulação computacional e desenvolve os elementos de um modelo matemático utilizado para reproduzir o comportamento físico-mecânico de uma massa de solo aplicável ao contexto da engenharia civil.
Palavras-chave: Simulação de computador, auto-aprendizagem, modelo científico, mecânica dos solos.
Introducción
El Ingeniero Civil requiere una adecuada comprensión acerca del comportamiento mecánico de los materiales que se utilizan para la construcción de obras civiles. Este conocimiento se afianza a través de dos tipos de estrategias pedagógicas que el estudiante de ingeniería civil adquiere de forma simultánea. La primera se refiere a la asimilación de los conceptos teóricos que sirven de fundamento para la conceptualización de los fenómenos físico-mecánicos y que usualmente se concretan en modelos de comportamiento. Dichos modelos pueden ser de tipo teórico, estocástico, empírico, entre otros.
La segunda estrategia consiste en la experimentación directa por parte del estudiante. Esta experimentación se lleva a cabo en laboratorios técnicos donde se ponen a prueba los materiales de ingeniería mediante ensayos especializados. El tipo y variedad de ensayos dependen de la clase de material a caracterizar y de las propiedades físicas, químicas o mecánicas que se desea obtener. En ciertos casos se utilizan modelos físicos a escala reducida o inclusive a escala real para estudiar el comportamiento de estructuras civiles ante condiciones externas debidamente controladas.
1. Metodología
La experiencia en laboratorio puede ser aprovechada al máximo por parte de los estudiantes y lograr un aprendizaje significativo, cuando previamente se efectúa una adecuada preparación de sus prácticas. Esta preparación contempla el estudio de las normas de ensayo aplicables, el procedimiento de ensayo, el procesamiento de la información y la forma de analizar los resultados que se pueden esperar de la práctica. La fase de preparación puede resultar más fructífera si se utilizan métodos modernos de enseñanza basados en herramientas tecnológicas tales como la simulación por computador.
2. Discusión
La simulación por computador es un programa informático de enseñanza-aprendizaje utilizado en casi todos los campos de la ciencia. La simulación por computador es un nuevo desafío en educación (Bossard, Kermarrec, & Buche, 2008) que se ha utilizado profusamente como herramienta de aprendizaje en áreas de la salud (Ross, Obeso, & Issenberg, 2008; Palter & Grantcharov, 2010; Sanford, 2010); negocios (Tompson & Tompson, 1995); ingeniería química (Mackenzie, Earl, Allen, & Gilmour, 2001); logística (Rao, Stenger, & Wu, 1992); entre otros.
La simulación por computador es de vital importancia para relacionar conceptos abstractos con condiciones reales. En el entrenamiento militar, por ejemplo, se utiliza la simulación por computador cuando las condiciones reales sugieren algún peligro o consumo de recursos físicos valiosos. En esta situación, se aprenden valiosas lecciones en un ambiente virtual seguro y económico como pueden ser las prácticas de tiro en polígono. Esta simulación no reemplaza la práctica real en terreno pero sirve para que los militares fortalezcan ciertos componentes de coordinación que inciden en la habilidad para optimizar su puntería y en general su destreza con el manejo de las armas. De esta forma se reduce el consumo de insumos requeridos en la práctica y se disminuyen los riesgos, sin perjuicio del logro de los objetivos que ésta busca. García (1995) expone varias ventajas de la simulación por computador en contraste con las prácticas de laboratorio o de campo, entre las cuales caben destacar: (1) el surgimiento de nuevas alternativas pedagógicas; (2) el costo de adquisición, mantenimiento y actualización del equipo de laboratorio puede ser más costoso que el equipo de cómputo y sus programas; y (3) se garantizan condiciones de seguridad en un ambiente virtual de aprendizaje.
La implementación de herramientas de simulación en el contexto del programa de ingeniería civil de la Escuela Militar, en particular en aquellos saberes que tienen un componente práctico, puede contribuir a complementar la práctica de laboratorio e inclusive pueden servir para que el estudiante saque aún más provecho de la misma. En la literatura pueden consultarse diversos estudios de caso. Por ejemplo, Kubota, Cho & Kajiwara (2007) reportan la utilización de simulación por computador para la enseñanza en una carrera de tecnólogos en laboratorio. Fernández (2005) estudió la influencia de un entorno de simulación en la enseñanza de la física en bachillerato. Por lo demás, los avances en el conocimiento de los fenómenos naturales, permite desarrollar herramientas de aprendizaje para modelar dichos fenómenos y presentarlos en un ambiente virtual (Pitarma, Ramos, Ferreira, & Carvalho, 2004).
3. Principios de la simulación por computador aplicada a la enseñanza
Pogrow (1994) presenta una estrategia de aprendizaje para desarrollar habilidades superiores de pensamiento en los educando, a partir de tres principios:
Creación de un ambiente de aprendizaje motivador,
Combinación de experiencias de aprendizaje visuales e interactivas que ayuden a los estudiantes a formar representaciones mentales, y
Desarrollo de una arquitectura cognitiva que integre experiencias de aprendizaje.
La simulación por computador puede ofrecer estas características de forma que el estudiante pueda explicar en sus propias palabras los eventos estudiados y desarrollar sus habilidades en la resolución de problemas. Jong (1991) aduce que la simulación por computador con propósitos de aprendizaje debe tener cuatro características:
Se trata de un modelo formal y manipulable que cumple los requerimientos de modelos cuantitativos o cualitativos para el procesamiento sistémico de información, de modo que el resultado esperado guarde coherencia con la información que se ingresa.
Sus metas de aprendizaje contemplan aspectos pedagógicos inherentes a la adquisición de conocimiento acerca del comportamiento del modelo (conocimiento conceptual), y el aprendizaje de procedimientos específicos (conocimiento operacional cognitivo o sicomotor).
La eficacia de sus procesos específicos de aprendizaje está en función de las metas de aprendizaje que se deben alcanzar en términos de capacidades del estudiante para formular una hipótesis de trabajo, ejecutar simulaciones y sacar conclusiones.
Sus actividades de aprendizaje son flexibles, de modoque el estudiante puede manipular elementos del modelo, tales como las variables de entrada y salida, conforme a la selección de parámetros.
Una característica adicional que distingue la simulación por computador de la modelación por computador es que en esta última el usuario puede adicionar, modificar o eliminar relaciones variables, parámetros y aún relaciones entre éstos para que el modelo pueda asemejarse más a la realidad.
Por otra parte, Jong (1991) divide en cuatro componentes las características que debe tener un ambiente inteligente de simulación para el aprendizaje:
Dominio: el modelo en que se basa la simulación debe representar una realidad en un campo específico del conocimiento. Dependiendo de la naturaleza del fenómeno estudiado, el modelo deberá tener cierto grado de complejidad, no solamente en las variables y parámetros involucrados sino en el procesamiento de los datos para producir los resultados.
Estudiantes: los estudiantes deben tener un mínimo de características cognitivas y no cognitivas para que puedan interactuar con las simulaciones. Estas características incluyen un conocimiento previo del dominio en que la simulación se desempeña como en los procesos de autoaprendizaje que demanda esta técnica de estudio.
Tutorías: un sistema de tutoría inteligente que guíe al estudiante durante el proceso.
Interface de aprendizaje: la interface permite la comunicación del estudiante con el sistema, haciendo que la información sea fácil de seleccionar y manipular, permitiendo que el estudiante pueda transformar rápidamente sus ideas en información de entrada y que la información de salida pueda ser presentada convenientemente en forma de datos, tablas o gráficas.
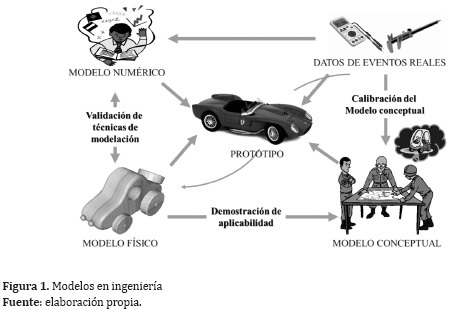
4. Modelos en ingeniería
La interrelación de los diferentes modelos utilizados en los procesos de análisis y diseño en ingeniería se puede observar en la Figura 1. En primer lugar se hace un análisis por parte del ingeniero acerca de la interrelación entre las variables más importantes que inciden en el fenómeno estudiado. De este análisis se desprende un modelo conceptual que se constituyen en una primera aproximación y que permite formular hipótesis sobre la respuesta que el sistema tendrá ante una acción externa.
El modelo conceptual permite diseñar un modelo matemático que interrelaciona las variables de entrada, la transformación que el sistema hace de éstas (función de trasferencia) y los resultados o variables de salida. Este modelo matemático es apenas una explicación que el hombre hace de un fenómeno natural que observa y en esa medida, es una aproximación cuyo grado de cercanía con la realidad, dependerá del grado de sofisticación del modelo matemático y la inclusión en menor o mayor grado de todas las variables que inciden en el resultado. Los modelos matemáticos podrán ser de tipo determinístico en donde las relaciones entre las diferentes variables que intervienen en el fenómeno son conocidas plenamente (por ejemplo las leyes de Newton), o podrán ser estocásticos, en donde dichas relaciones se conocen de forma aproximada por observación y por tanto existe cierto grado de incertidumbre (por ejemplo el estado del tiempo en una región).
En ocasiones el modelo numérico o matemático no puede formularse explícitamente o no puede ser utilizado directamente para resolver el problema, dada la complejidad de la realidad que requiere ser modelada. En estos casos un modelo numérico puede contribuir a buscar representar el problema. El modelo numérico utiliza técnicas numéricas de aproximación mediante cálculos sucesivos que se van aproximando a la realidad o la subdivisión del conjunto en partes más pequeñas en donde el modelo matemático es válido y manejable, generando ecuaciones de compatibilidad entre dichas partes y resolviendo un sistema de ecuaciones simultáneas dadas unas condiciones de frontera conocidas. Debido a la cantidad de cálculos que se requieren para llegar a una solución satisfactoria, los modelos numéricos requieren la utilización de computadores.
La verificación de los modelos conceptual y numérico se realiza mediante la experimentación directa en un modelo a escala en donde se realizará un registro cuantitativo de la evolución de las diferentes variables. Un modelo por definición, es apenas una aproximación de la realidad y por consiguiente contiene únicamente los detalles que el modelo conceptual considera relevantes. En consecuencia, los resultados obtenidos del modelo físico también se consideran una aproximación, pero podrán servir para validar u objetar el modelo conceptual, matemático o numérico que le precede.
Finalmente, el prototipo es un modelo a escala real en el que se han incluido todos los pormenores que el objeto de análisis tiene y sobre el cual se realizará una verificación final. El prototipo en consecuencia se puede utilizar en aquellos casos en que se hace un diseño de ingeniería y que se quiere someter a prueba antes de su producción en serie.
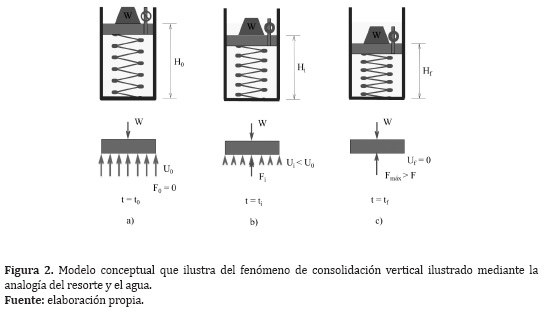
5. Simulación del proceso de consolidación vertical de una masa de suelo
En mecánica de suelos, el fenómeno de consolidación es el proceso mediante el cual una masa de suelo reduce su volumen debido a la migración del agua, la cual se causa por un cambio en el estado de esfuerzos producido por ejemplo por la aplicación de una carga sobre el depósito de suelo. La teoría de la consolidación fue formulada por Karl Terzaghi en 1923 (Ellis & Darby, 2005). Si bien no es la única teoría al respecto, ni la más reciente (Cf. Biot, 1941) es la más difundida y aplicada en la práctica corriente. La Figura 2 ilustra el modelo conceptual en que se basa esta teoría. En este caso, el proceso físico mecánico se representa mediante una analogía en la que en el interior de un recipiente hermético lleno de agua se coloca un resorte que soporta una tapa móvil, la cual evita la salida de agua. Esta tapa tiene una pequeña válvula que se puede abrir y cerrar a voluntad. En la Figura 2a) se coloca una masa W en la parte superior de la tapa, mientras que la válvula se mantiene cerrada. En este instante inicial la tapa no puede descender como producto de esta carga, puesto que el agua se considera un líquido incompresible. En el diagrama de cuerpo libre de la tapa que se presenta en la parte inferior, se muestra cómo se desarrolla una presión uniforme U0 en el superficie de la tapa A, para equilibrar el peso de la masa (W = U0xA). El resorte no efectúa ninguna fuerza ya que no sufre deformación. En la Figura 2b), representa el instante ti en que la pequeña válvula se ha abierto y como consecuencia, el agua que en el interior del recipiente está sometida a presión, comienza a drenar hacia el exterior. Esta reducción en el volumen se manifiesta en un descenso de la altura de la tapa. En ese instante el resorte se deforma y ejerce una fuerza Fi hacia arriba sobre la tapa y la presión en el interior del recipiente disminuye hasta un valor Ui. La ecuación de equilibrio de la tapa es en consecuencia: W = UixA + Fi
La velocidad del proceso depende de varios factores, principalmente de la capacidad de la válvula para evacuar agua. La Figura 2c) presenta el estado final del proceso en el instante tf cuando la presión del agua llega a ser nula y la fuerza en el resorte Fmáx alcanza un valor máximo igual a la carga W. El proceso no continúa puesto que la presión en el interior del recipiente vuelve a ser igual a la presión atmosférica. La tapa desciende hasta alcanzar una altura final Hf. La diferencia entre la posición inicial y la posición final de la tapa se define como asentamiento.
Los elementos de una masa de suelo que corresponden a la anterior analogía son los siguientes: la masa sobre la tapa simula la carga externa que se aplica en la superficie del terreno cuando se construye una obra civil, la cual produce un incremento en el esfuerzo vertical sobre el terreno, Δσv ; el resorte representa los granos de suelo que conforman el esqueleto sólido de la masa de suelo; el agua en el recipiente corresponde al fluido (generalmente agua) que ocupa los espacios intergranulares o poros; la presión del agua es análoga al exceso de presión del fluido presente en los espacios intergranulares, μe, causada por la aplicación de la carga externa; la altura inicial del resorte representa el espesor inicial de la masa de suelo, o más exactamente la máxima distancia de drenaje de la capa de suelo, H0; y la válvula representa el coeficiente de permeabilidad vertical del suelo, kv, es decir la facilidad con que el agua puede fluir a través de este medio poroso.
En la analogía, la carga externa es equilibrada inicialmente por un incremento en la presión del agua dentro del recipiente, la cual paulatinamente se va reduciendo hasta llegar a ser nula, mientras la fuerza en el resorte inicialmente es cero hasta llegar a un valor máximo, equivalente a la carga externa. De esta misma forma, el cambio en el esfuerzo vertical externo, Δσv, inicialmente se traduce en un exceso de presión intersticial, μe que gradualmente se va disipando mientras que se incrementa el esfuerzo vertical efectivo sobre las partículas sólidas, σ'v.
Este modelo conceptual se describe matemáticamente mediante la siguiente ecuación diferencial parcial de segundo orden:
En donde cv es el coeficiente de consolidación vertical:
e: relación de vacíos o proporción en volumen, de espacios intergranulares con respecto al volumen de granos sólidos presentes en la masa de suelo
γw: peso unitario del agua
av: coeficiente de compresibilidad vertical, definido como la relación entre el cambio en la relación de vacíos y el cambio en el esfuerzo efectivo, similar a la flexibilidad del resorte en la analogía de Terzaghi
z: cota de un punto dentro de la masa de suelo con respecto a un nivel de referencia
t: tiempo
La anterior ecuación tiene solución si se conocen ciertas condiciones de frontera, que corresponden a los excesos de presión de poros al inicio y al final del proceso, y este mismo valor en los extremos superior e inferior de la masa de suelo para cualquier instante de tiempo. Esta solución se expresa en términos de un indicador adimensional que permite evaluar la evolución del fenómeno de consolidación en función del tiempo, denominado grado promedio de consolidación, :
Donde Tv se denomina factor vertical adimensional de tiempo que se expresa así:
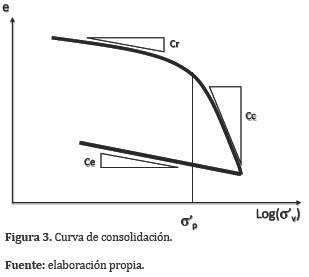
El coeficiente de consolidación vertical y la variación de la relación de vacíos con el esfuerzo efectivo, se obtienen experimentalmente en laboratorio a través del ensayo de consolidación vertical. En la Figura 3 se presenta dicha variación, de la cual se pueden destacar los siguientes elementos:
σ'p: Esfuerzo de preconsolidación, esfuerzo a partir del cual la pendiente de la curva aumenta notoriamente y que corresponde al máximo esfuerzo que la masa de suelo ha soportado en su historia.
Cr: Coeficiente de recompresión, pendiente de la rama inicial antes de alcanzar el esfuerzo de preconsolidación.
Cc: Coeficiente de compresión normal, pendiente de la rama de compresión virgen, donde el esfuerzo alcanzado es mayor al esfuerzo de preconsolidación.
El cambio en la relación de vacíos, Δe, al final del proceso de consolidación, como producto de la aplicación de una carga externa puede calcularse mediante una de las siguientes expresiones:
Donde σ'0 es el esfuerzo vertical efectivo antes de la aplicación de la sobrecarga. El cambio en la relación de vacíos está directamente vinculado con la magnitud del asentamiento que se puede esperar al final del proceso de consolidación, Sf
Donde e0 es la relación de vacíos inicial de la masa de suelo. El asentamiento vertical para cualquier tiempo, S(t) se estima así:
A continuación se describen las variables de entrada, parámetros del suelo, constantes físicas y variables de salida del modelo matemático presentado anteriormente.
Información de entrada:
Variables que corresponden a las condiciones iniciales del terreno:
- Relación de vacíos inicial, e0
- Esfuerzo vertical efectivo inicial, σ'0
- Máxima distancia de drenaje de la masa de suelo, H0
Parámetros mecánicos del suelo:
- Coeficiente de permeabilidad vertical, kv
- Coeficiente de compresibilidad vertical, av
- Esfuerzo de preconsolidación, σ'p
- Coeficiente de recompresión, Cr
- Coeficiente de compresión normal, Cc
Constantes físicas:
- peso unitario del agua, γw
Cargas externas:
- Incremento del esfuerzo vertical, Δσv
Información de salida:
- Asentamiento total, Sf|
- Tiempo necesario para que se alcance el asentamiento total, tf
Opciones de entrada:
Se refiere a las alternativas para el ingreso de la información de entrada, tales como fgráficas, ábacos o tablas con valores típicos de las variables de entrada o correlaciones empíricas con otras propiedades físicas.
Opciones de salida:
Estas opciones se utilizan para seleccionar diferentes formas de presentar los resultados, ya sea a través de tablas, gráficas o animaciones.
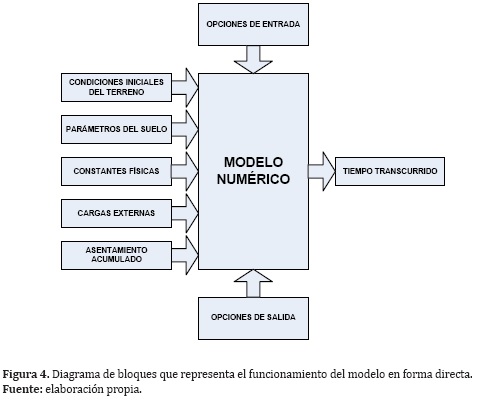
El diagrama de bloques de la Figura 4 representa el funcionamiento del modelo indicando las variables y parámetros de entrada, opciones de entrada y salida y las variables de salida que representan el funcionamiento del sistema cuando se resuelve de forma directa. En este caso las variables de salida (asentamiento acumulado al cabo de un tiempo determinado) se resuelven a partir de las variables y parámetros de entrada y las ecuaciones que las relacionan.
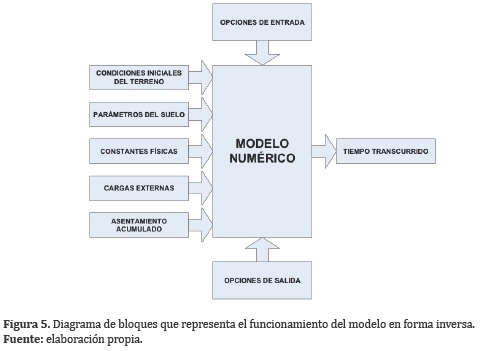
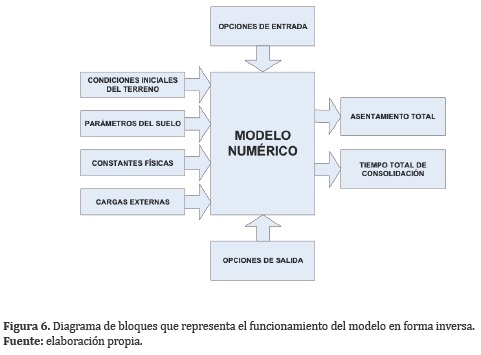
En la Figura 5, el sistema debe resolverse de forma inversa, pues las variables de salida (tiempo necesario para alcanzar cierto asentamiento) no se encuentran aisladas de forma explícita y por consiguiente el sistema debe realizar un proceso iterativo para encontrar el resultado. Por último la Figura 6, muestra un caso combinado en el cual se obtienen varios resultados (asentamiento y tiempo correspondiente), unos se pueden resolver de forma directa pero otros deben resolverse por iteraciones.
La implementación del modelo matemático en computador debe acudir a un modelo numérico para poder solucionar el problema, especialmente en aquellos casos en donde se deben resolver problemas inversos, como por ejemplo encontrar el tiempo necesario para que se alcance un asentamiento determinado. También es necesario implementar una rutina numérica finita para encontrar una respuesta suficientemente aproximada a la sucesión infinita de la Ecuación 3.
6. Metas de aprendizaje
Las metas de aprendizaje que se proponen con la implementación de esta simulación por computador se refieren a:
Adquisición de conocimiento acerca del comportamiento de una masa de suelo cuando es sometida a una carga vertical. Este comportamiento se caracteriza por el asentamiento vertical y el tiempo necesario para que éste se produzca.
Familiarización con valores y rangos usuales.
Las variables y parámetros de entrada, están limitados en la práctica de ingeniería dentro de rangos en los que usualmente se encuentran dichos valores, de acuerdo con la naturaleza de cada tipo de suelo.
Con frecuencia algunos parámetros están empíricamente correlacionados con propiedades físicas de fácil determinación. De la misma forma, los resultados deberían guardar concordancia con los datos de entrada, así que el estudiante debe aprender a analizar críticamente los resultados producidos por la simulación, por ejemplo comparar los resultados con los valores límites para diseño establecidos en la norma sismo resistente colombiana (NSR-10).
7. Procesos de aprendizaje
El proceso de aprendizaje de la simulación del fenómeno de consolidación se divide en las siguientes etapas.
Formulación de una hipótesis sobre las variables que tienen mayor importancia en el resultado para el ejercicio en particular a resolver y la tendencia que debería observarse en los resultados.
Selección de las variables de entrada y salida, así como la forma de selección y presentación de los mismos (tablas o gráficas)
Selección de los valores de entrada de acuerdo con información dada por el enunciado
Análisis de los resultados a través de preguntas que se hacen sobre el aspecto de los resultados, tendencias observadas, relaciones causa-efecto.
Formulación de conclusiones a partir de preguntas concretas sobre los resultados
A continuación se presenta el planteamiento de ejercicios que se pueden implementar en la simulación y las metas de aprendizaje para cada una de ellas:
Asentamiento total y periodo necesario para que el mismo que se produzca por una carga sobre un estrato de suelo arcilloso normalmente consolidado que reposa sobre un suelo más rígido e impermeable. Análisis de sensibilidad variando parámetros de entrada de forma controlada.
Conclusión
En el presente artículo se presentaron las condiciones pedagógicas requeridas para el diseño de una herramienta de simulación para el aprendizaje, desarrollando este marco conceptual en la aplicación concreta de esta estrategia pedagógica en la enseñanza del fenómeno de consolidación que se estudia en mecánica de suelos de ingeniería civil.
El estudio previo de los objetivos, condiciones y metas que debe tener una herramienta de simulación computacional con fines de enseñanza, ayuda a que dicha herramienta contribuya efectivamente en el proceso de aprendizaje de los estudiantes. Esta metodología no siempre se aplica en la práctica, por lo que con frecuencia las herramientas de simulación no satisfacen las expectativas de los estudiantes, desaprovechando recursos de la institución y de los estudiantes.
En relación con la eficiencia del aprendizaje asistido por computador, cabe destacar que el aprendizaje asistido por computador ha demostrado ser de gran utilidad en diversos campos del conocimiento gracias a las posibilidades de interacción que ofrece (Liao & Chen, 2007). Sin embargo, un aspecto que es de difícil evaluación es saber cómo contribuye este tipo de asistencia al proceso de aprendizaje puesto que a pesar de que se puedan utiliza instrumentos de evaluación previa y posterior a la utilización de la herramienta de simulación por computador enfocada al aprendizaje, no es fácil deducir que las diferencias observadas se deban exclusivamente a la utilización del computador (Scalon et al., 1998). Otro estudio realizado por (Finkelstein, y otros, 2005) en el ámbito de un curso de física a nivel universitario, utilizando simulación por computador para el aprendizaje de conceptos relacionados con circuitos eléctricos, demostró que esta simulaciones diseñadas y utilizadas apropiadamente, produjeron un mejor rendimiento de los estudiantes en la apropiación de los conceptos. Adicionalmente los estudiantes que utilizaron estas herramientas tuvieron un mejor desempeño en la posterior manipulación de los componentes eléctricos en laboratorio.
En el aprendizaje asistido por computador existen dos efectos: el primero, conocido como el efecto de interactividad (Betrancourt, 2005) indica que el conocimiento se asimila más fácilmente en la medida que el estudiante pueda tener mayor control sobre el simulador y éste a su vez responda a los cambios inducidos por el estudiante (alta interactividad). El segundo, llamado efecto reverso de experticia, propuesto por (Kalyuga, Ayres, Chandler, & Sweller, 2003) indica que las técnicas de aprendizaje que son altamente efectivas con estudiantes con poco conocimiento previo pueden perder su efectividad e inclusive tener consecuencias negativas cuando son utilizadas con estudiantes con mayor conocimiento.
Los dos efectos combinados han mostrado evidencias (Park, Lee, & Kim, 2009) de que en ambientes de simulación con mayor nivel de interactividad,mejora la eficiencia en el proceso de aprendizaje en estudiantes con mayores niveles de conocimiento previo. En contrapartida, los estudiantes con menores niveles de conocimiento previo tuvieron mayor eficiencia en el proceso, cuando utilizaron simulaciones con menores niveles de interactividad. En consecuencia, el diseño de la herramienta de simulación debe guardar concordancia con el nivel de preparación que los estudiantes a los cuales se va a destinar.
Agradecimientos
Los autores agradecen el apoyo de la Escuela Militar de Cadetes "General José María Córdova" para el desarrollo de la investigación en la que se enmarca el presente artículo.
Referencias
1. Betrancourt, M. (2005). The animation and interactivity principles in multimedia learning. In R. E. Mayer, The Cambridge handbook of multimedia learning (pp. 287-296). [ Links ]
2. Bossard, C., Kermarrec, G., & Buche, C. (2008). Transfer of learning in virtual environments: a new challenge? Virtual Reality, 12 (3), 151-161. [ Links ]
3. Fernández, J. (2005). Estudio de la influencia de un entorno de simulación por ordenador en el aprendizaje por investigación de la Física en Bachillerato. [ Links ]
4. Finkelstein, N. D., Adams, W. K., Keller, C. J., Perkins, K. K., Podolefsky, N. S., Reid, S., et al. (2005). When learning about the real world is better done virtually: A study of substituting computersimulations for laboratory equipment. Physical REview Special Topics, Physics Education Research, 010103, 1-8. [ Links ]
5. Garcia, J. R. (1995). Use of technology in developing problem-solving/critical thinking skills. Journal of Industrial Technology, 11 (1), 14-17. [ Links ]
6. Jong de, T. (1991). Learning and instruction with computer simulations. Education & Computing, 6, 217-229. [ Links ]
7. Kalyuga, S., Ayres, P., Chandler, P., & Sweller, J. (2003). The expertise reversal effect. Educational Psychologist, 38 (1), 23-31. [ Links ]
8. Kubota, T., Cho, Y., & Kajiwara, M. (2007). Use of a computer-assisted simulation system in undergraduate education of laboratory technologists. The Japanese journal of clinical pathology55, 55 (6), 517-521. [ Links ]
9. Liao, Y.-K., & Chen, Y.-W. (2007). The effect of computer simulation instruction on student learning: a meta-amalysis of studies in Taiwan. Journal of information Technology and Applications, 2 (2), 69-79. [ Links ]
10. Mackenzie, J. G., Earl, W. B., Allen, R. M., & Gilmour, I. (2001). A computer simulation in chemical engineering education. Journal of Engineering Education, 90 (3), 331. [ Links ]
11. Palter, V., & Grantcharov, T. (2010). Simulation in surgical education. Canadian Medical Association, 182, 1191-1196. [ Links ]
12. Park, S., Lee, G., & Kim, M. (2009). Do students benefit equally from interactive computer simulations regardless of prior knowledge levels? Computers & Education, 649-655. [ Links ]
13. Pitarma, R., Ramos, J. .., Ferreira, M. E., & Carvalho, M. G. (2004). Computational fluid dynamics: An advanced active tool in environmental management and education. Management of Environmental Quality, 15 (2), 102-110. [ Links ]
14. Pogrow, S. (1994). Students who just don't understand. Educational Leadership, 52 (3), 62-66. [ Links ]
15. Rao, K., Stenger, A. J., & Wu, H.-J. (1992). Integrating the Use of Computers in Logistics Education. International Journal of Physical Distribution & Logistics Management, 22 (2), 3. [ Links ]
16. Ross, S., Obeso, V., & Issenberg, B. (2008). Simulation Technology for Skills Training and Competency Assessment in Medical Education. Journal of General Internal Medicine, 23, 46-49. [ Links ]
17. Sanford, P. (2010). Simulation in Nursing Education: A Review of the Research. The Qualitative Report, 4, 1006-1011. [ Links ]
18. Scalon, E., Tosunoglu, C., Jones, A., Butcher, P., Ross, S., Greenberg, J., et al. (1998). Learning with computers: experiencies of evaluation. Computers Educ., 30 (1/2), 9-14. [ Links ]
19. Tompson, G., & Tompson, H. (1995). Using computer simulations for group projects in business school education. Journal of Education for Business, 71 (2), 97. [ Links ]