Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares en
SciELO
Similares en
SciELO -
 Similares en Google
Similares en Google
Compartir
Revista Científica General José María Córdova
versión impresa ISSN 1900-6586
Rev. Cient. Gen. José María Córdova vol.14 no.17 Bogotá ene./jun. 2016
RECENSIÓN 1
Solution for Fermat's Last Theorem
Mathematical Recension (English)
By the Colombian Navy Vice Admiral José William Porras Ferreira
Colombian Navy, Bogota, Colombia.
Abstract.
Fermat's Last Theorem (FLT), (1637), states that if n is an integer greater than 2, then it is impossible to find three natural numbers x, y and z where such equality is met being (x,y)>0 in xn + yn = zn.
This paper shows the methodology to prove Fermat's Last Theorem using Reduction ad absurdum, the Pythagorean Theorem and the property of similar triangles, known in the 17TH century, when Fermat enunciated the theorem.
Key Words: Fermat's Last Theorem, Pythagorean Theorem, Reduction ad absurdum, similar triangles.
Introduction
Fermat's last theorem (FLT) or Fermat-Wiles's theorem is one of the most famous theorems in the history of mathematics [1]-[2]-[3]. The unsolved problem stimulated the development of algebraic number theory in the 19th century and the proof of the modularity theorem in the 20th century. Prior to the proof by Andrew Wiles (1995), [4]-[5]-[6] it was one of the "most difficult mathematical problems".
Using modern notation, Fermat's last theorem can be stated as follows:
If n is an integer greater than 2, then it can't be found three natural numbers x, y and z such that the equality is met being (x,y)>0 in:
xn+yn=zn
Pierre de Fermat (1667) [7], showed the case of n=4, using the infinite descent technique. Alternative proofs of the case n=4 were developed later [8]; Leonard Euler (1735), demonstrated the n=3 case confirmed in 1770, [9]-[10]-[11]. Later Germain, [12], stated that if p and 2p+1 are both primes, then the expression for the Fermat conjecture for the p power, meant that one of the x, y or z would be divisible by p. Germain tested for numbers n<100 and Legendre, extended their methods for n<197. Dirichlet and Legendre, (1823-1825), [13]-[14], extended the case of n=3 to n=5. Lame (1840), [15]-[16], proved the case of n=7. Fermat's Last Theorem has also been proven for the exponents n = [6, 10, 14].
Andrew Wiles in 1995 [6] finally attained a general test for all the exponents greater than 2, Wiles could prove Fermat's last theorem from the connection, outlined by Frey, and demonstrated by Ken Ribet in 1985 [17-18], that a demonstration of the so-called Taniyama-Shimura conjecture [19-20], would directly lead to a demonstration of Fermat's last theorem. In short, the Taniyama-Shimura conjecture states that every elliptic curve may be uniquely associated with a mathematical object called a modular. If the UTF is false, then there would be an elliptic curve such that can't be associated with any modular form, and therefore the Taniyama-Shimura conjecture would be false. I.e., Taniyama-Shimura conjecture solution would demonstrate the UTF.
The demonstration of the Taniyama-Shimura conjecture was already on a challenge of the utmost importance, because that was one of the points of the so-called Langlands program, whose goal is to unify areas of mathematics which apparently have no unrelated. Wiles spent 8 years following the demonstration of Ribet in complete isolation working on the problem and only relying on his wife, which is a way of working unusual in mathematics, where it is common to mathematicians from around the world to share their ideas often. To not raise suspicion, Wiles was publishing articles periodically, as any mathematician of any University in the world would. Their initial study meant the first significant advance in the theory of Galois prior to an attempt to extend the Iwasawa theory with an inductive argument (1990-1991). When it seemed that it stagnated, he sought other directions. In the summer of 1991, he seek in Iwasawa theory solutions but also seemed not to reach the central themes to solve the UTF. In response, approached colleagues to look for any hint of cutting-edge research and new techniques, and discovered a system of Euler recently developed by Victor Kolyvagin and Matthias Flach which seemed to measure for the inductive part of his test. Wiles studied and extended this approach, in January 1993 asked his colleague at Princeton, Nick Katz, to check their reasoning. Its conclusion at the time was that the techniques used by Wiles seemed to work properly. ([2] pp 209-232) but had subtle errors that Wiles finally corrected and successfully completed its demonstration in 1995 [21-22-23].
Because Wiles used more than 100 pages and modern mathematical techniques, is in practice impossible that this demonstration is the same one that hinted at Fermat. (Fermat had a copy of the "Arithmetica of Diophantus' on whose banks scoring reflections that were emerging him. In one of these margins it enunciated the theorem and wrote in Latin: "Cuius rei demonstrationem mirabilem sane detexi. Hanc marginis exiguitas non caperet", whose translation is: "I have a truly marvelous demonstration for this fact, but this margin is too narrow to contain it". Although Fermat in 1667, proved the case n = 4, using the method of infinite descent; it is likely that him had deceived to believe that he had a proof for the general case. It can be even that will have noticed his error further: their marginal notes were for personal use, and therefore Fermat would have not had to backtrack with their corresponding.
On October 7, 2013 I was invited to Paris by WASET (World Academy of Science Engineering and Technology) to give a lecture on the demonstration of the last theorem of Fermat, using mathematical tools that existed in the 17TH century, which was published by WASET [24]. Here is an even more condensed solution and was presented at the invitation of the Department of Physics of the Universidad del Valle Cali, Colombia on December 4, 2014.
Definitions
Definition 1. Primitive Pythagorean Triples:
A Pythagorean triple is a set of three positive integers a,b, and c having the property that they can be respectively the two legs and the hypotenuse of a right triangle, thus satisfying the equation a2 + b2= c2; the triple is said to be primitive if and only if a,b, and c share no common divisor. No primitive triple appears more than once.
Definition 2. Tree of primitive Pythagorean triples:
In mathematics, a tree of primitive Pythagorean triples is a data tree in which each node branches to three subsequent nodes with the infinite set of all nodes giving all (and only) primitive Pythagorean triples without duplication. This was first discovered by B. Berggren in 1934, [38].
Definition 3. Coprimes.
Let a and b two integers, some of them can differ from zero. The greatest common divisor (gcd) on a and b is the largest positive integer d noticed by (a,b) = d that divides both a and b. In the case in which (a,b) = 1, we say that a and b are coprimes.
Definition 4. Reduction ad absurdum:
The reduction ad absurdum is a mode of argumentation that seeks to establish a contention by deriving an absurdity from its denial, thus arguing that a thesis must be accepted because its rejection would be untenable. It is a style of reasoning that has been employed throughout the history of mathematics and philosophy from classical antiquity onwards.
Theorems
Theorem 1
In the Equation xn + yn = znn It is always true that: (zn for n = 2) > (zn for n > 2)
Demonstration
-
Let xn + yn =znn for n >1 ⇒ (x<y)∈ Z+-{0}1
-
It is clear that y < zn
-
Let z22= x2 + y2 for n = 2 and zn>2n = xn + yn for n > 2
-
Comparing equations (1) and (2), obviously it must be:
For z2n:



Corollary: In the Equation:
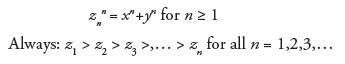
Demonstration
Following the same procedure of Theorem 3.1, assuming for n > 3, that z33= x3 + y3 and zn>3n = xn + yn and so on.
Theorem 2. Fermat's Last Theorem (FLT)
In the Equation zn>2n = xn + yn for n > 2 and (x,y) ∈Z+ - {0}, there are no solutions with non-zero positive integer, (FLT).
Demonstration by Reduction ad absurdum:
-
Assuming that zn>2n = xn + yn for n > 2 has a minimum solution with non-zero positive integers (zn>2, x,y) ∈Z+ - {0}, where (x,y) are coprimes and x ≠ y otherwise zn>2 = √2x will be irrational. For convenience it is assumed x < y and therefore y < zn>2.
-
According to Theorem 1: z1> z2> z3>, ... > zn for all n = 1,2,3,...
-
Porras-Ferreira [29], showed that in the equation z22 = x2+ y2 since z2 > y, then z2= y+m where [z2 = (y+m)2]≡[z2 = x2 + y2] ⇒
 In the case of the primitive Pythagorean triples (x, y, z2) where (x,y) are coprimes, m is a positive integer not null.
In the case of the primitive Pythagorean triples (x, y, z2) where (x,y) are coprimes, m is a positive integer not null.In all other cases, m is not a natural number and (x, y, z2) are not Pythagorean triples with integer numbers (z2 is an irrational number, same for m).
-
As zn>2 y then zn>2 = y + q where q must be a non-zero positive integer.
Therefore:
[zn>2n= (y + q)n]≡[zn>2n = xn + yn]
As z2= y + m > zn>2 = y + q, therefore m > q.
As m >q then m - a = q where a must be a non-zero positive integer i.e. (m,q,a) must be a non-zero positive integer.
Therefore:
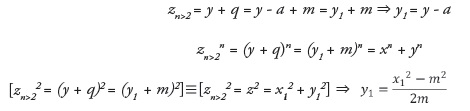
-
The minimum solution of z(n>2) with (x,y) coprimes, implies that x1 < x and y1 < y, where x1 and y1 must be non-zero coprime positive integers.
If (x1, y1) are no non-zero coprime positive integers, then zn>2will not have a minimal solution in non-zero positive integers and the assumed in 1. is false.
As y1 < y and y1 is a non-zero positive integer then:
The Pythagorean triangles (z1, x, y) and (zn>2= z1, x1, y1) are similar triangles (its sides are parallel) then there should be a fractional number b >1 that divide to x and y, where
 and
and  but x,y) are coprimes (have no common divisors), therefore if b|y (b divide to y) and since y1 is a positive integer not null) then
but x,y) are coprimes (have no common divisors), therefore if b|y (b divide to y) and since y1 is a positive integer not null) then  , and
, and  (b does no divide to x), i.e. x1 is a fractional number of the form
(b does no divide to x), i.e. x1 is a fractional number of the form 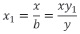 and x12 would also be fractional number, i.e. zn>2= x12 + y12 is not a non-zero positive integer (an integer cannot be equal to one integer more a fractional), therefore zn>2= √x12+ y12= √xn+ yn is not a non-zero positive integer and the assumed in 1. is false, being proved Fermat's last theorem by reduction ad absurdum.
and x12 would also be fractional number, i.e. zn>2= x12 + y12 is not a non-zero positive integer (an integer cannot be equal to one integer more a fractional), therefore zn>2= √x12+ y12= √xn+ yn is not a non-zero positive integer and the assumed in 1. is false, being proved Fermat's last theorem by reduction ad absurdum.
Note:
According to definitions 1 and 2, a Pythagorean triangle with primitive Pythagorean (all sides are integers), there can be no other Pythagorean triangle similar to the previous but with all its sides integers, because it contradicts the Pythagorean theorem. For the same reason, it is not necessary to expand the demonstration for the case of Pythagorean triangles (z2, x, y) that do not correspond to primitive Pythagorean triples, with irrational z2 and (x, y) ∈Z+ - {0}, because any Pythagorean triangle similar and lower sides (zn>2, x1, y1) cannot have integer solutions, (all sides (zn>2, x1, y1) ∈Z+ - {0}), because it contradicts the Pythagorean theorem.
Corollary:
In the Equation zn = xn + yn for n>2 if any x, y or z are irrationals of the form z = a(f⁄d) or x = b(h⁄g) or y=c(j/i) with (d, f),(g, h), (i, j) coprimes, (f>d, h>g, j>i) and (d, g, i) > 2 then there are not solutions in Z+ - {0}, since according to definitions 2.1 and 2.2, and Theorem 1, a Pythagorean triangle (z2,x, y) will not be a primitive Pythagorean triples (all sides are integers), because z22= (a(f⁄d)2 or x2 =(b(h⁄g))2or y2= (c(j⁄i))2 will be irrational number since (d, g, i)>2 , then can't be other Pythagorean triangle small and similar to the previous and lower sides (zn>2, x1, y1) with integer solutions (all sides (zn>2, x1, y1) ∈ Z+ - {0}), because it contradicts the Pythagorean theorem.
q.e.d.
Conclusion
A simple and wonderful demo using 17TH-century mathematical tools such as stated by Fermat in the margin of the "Arithmetica of Diophantus' writing your notes can exist. Taking into account that Fermat was who introduced the principle of infinite descent, which was used on his show for n=4k in the UTF, It wouldn't be strange that Fermat did think that he had a general solution of his last theorem or used a similar procedure to the described here.
The theorem doesn't have a major application, but to be considered the most difficult problem in the world, for 360 years, the search for its solution, allowed the advancement of mathematical science during the last four centuries and where great mathematicians such as Euler (1707-1783), Legrange (1736-1813), Germain (1776-1831), Gauss (1777-1855), Cauchy (1789-1857), Lamé (1795-1870), Dirichlet (1805-1859), Liouville (1809-1882) , Kumer (18101893), Vaudiver (1882-1973), Taniyama (1927-1958), Shimura (1930-), Wiles (1953-) and many other mathematicians who contributed to the advancement of the sciences and number theory in search of their show.
Acknowledgment
I'm grateful to many mathematicians and colleagues for their numerous comments along many years of research.
Notes
1 Z+-{0} means positive integers not including 0.
2 From Latin: Quod erat demonstrandum
References
1. Cox D. A. Introduction to Fermat's last theorem. Amer. Math. Monthly 101 (1), pp 3-14. 1994. [ Links ]
2. Singh S. Fermat's Last Theorem. London. ISBN 1-85702-521-0. 1997. [ Links ]
3. Ribenboim P., The history of Fermat's last theorem (Portuguese), Bol. Soc. Paran. Mat. (2) 5 (1), pp 14-32. 1984. [ Links ]
4. Van der Poorten A. Remarks on Fermat's last theorem, Austral. Math. Soc. Gaz.21 (5), pp 150-159. 1994. [ Links ]
5. de Castro Korgi R. The proof of Fermat's last theorem has been announced in Cambridge, England (Spanish), Lect. Mat.14, pp 1-3. 1993. [ Links ]
6. Wiles A. Modular elliptic curves and Fermat's Last Theorem (PDF). Annals of Mathematics 141 (3): pp. 443-531. Doi: 10.2307/211855, May 1995. [ Links ]
7. Heath-Brown D. R. The first case of Fermat's last theorem. Math. Intelligencer7 (4), pp 40-47. 1985. [ Links ]
8. Cox D. A. Introduction to Fermat's last theorem. Amer. Math. Monthly101 (1), pp 44-45. 1994. [ Links ]
9. Barlow P. An Elementary Investigation of Theory of Numbers. St. Paul's Church-Yard, London: J. Johnson. pp. 144-145. 1811. [ Links ]
10. Gautschi, W. Leonhard Euler: His Life, the Man, and His Work. SIAM Review 50 (1): pp 3-33. 2008. [ Links ]
11. Mačys J.-J. On Euler's hypothetical proof. Mathematical Notes 82 (3-4). pp 352-356. 2007. [ Links ]
12. Del Centina, A. Unpublished manuscripts of Sophie Germain and a revaluation of her work on Fermat's Last Theorem. Archive for History of Exact Sciences 62.4 (2008): pp 349-392. Web. September 2009. [ Links ]
13. Carmichael, R.-D. The Theory of numbers and Diophantine Analysis. Dover N. Y. 1959. [ Links ]
14. Legendre, A.M., Research on some analysis of unknown objects, particularly on Fermat's theorem (in French) Mem. Acad. Roy. Sci. Institut France 6: 1-60. 1823. [ Links ]
15. Lamé, G., Memory on Fermat's Last Theorem (in French). C. R. Acad. Sci. Paris 9. pp. 45-46. 1839. [ Links ]
16. Lamé, G., Memory of the undetermined analysis demonstrating that the equation x^7+y^7=z^7 is impossible in integer numbers (in French). J. Math. Pures Appl. 5: pp. 195-211, 1840. [ Links ]
17. Ribet K. Galois representation and modular forms. Bulletin AMS 32, pp 375-402. 1995. [ Links ]
18. Ribet, K. A. "From the Taniyama-Shimura Conjecture to Fermat's Last Theorem." Ann. Fac. Sci. Toulouse Math. 11, pp. 116-139, 1990. [ Links ]
19. Serge L. Some History of the Shimura-Taniyama Conjecture. Notices of the AMS. Volume 42, Number 11, pp 301-1307. November 1995. [ Links ]
20. Gerhard F. Links between stable elliptic curve and certain Diophantine equations. Annales Universitatis Saraviensis. Series Mathematicae 1 (1) iv+40. ISSN 0933-8268, MR 853387. 1986. [ Links ]
21. Gerd F. The proof of Fermat's Last Theorem R. Thaylor and A. Wiles. Notices of the AMS. Volume 42 Number 7, pp 743-746, July 1995. [ Links ]
22. Darmon H., Deamond F. and Taylor R. Fermat's Last Theorem. Current Developments in Math. International Press. Cambridge MA, pp 1-107. 1995. [ Links ]
23. Kleiner I. From Fermat to wiles: Fermat's Last Theorem Becomes a Theorem. Elem. Math. 55, pp. 19-37 doi: 10.1007/PL00000079. 2000. [ Links ]
24. Porras Ferreira J. W. Fermat's Last Theorem A Simple Demonstration. International Journal of Mathematical Science. Vol 7 No.10, pp 51-60. 2013. [ Links ]