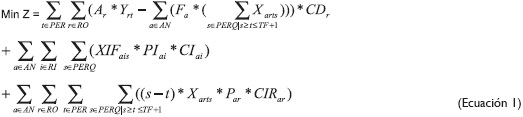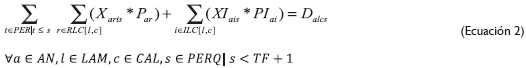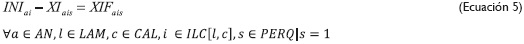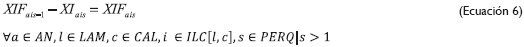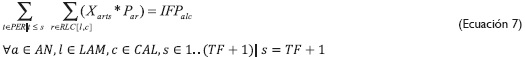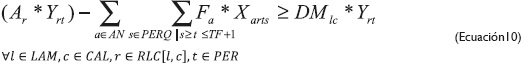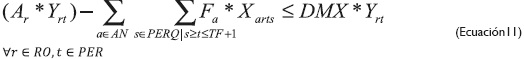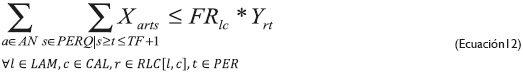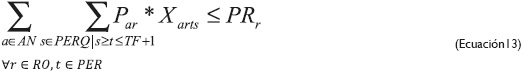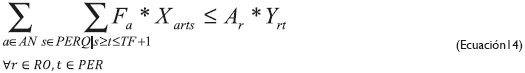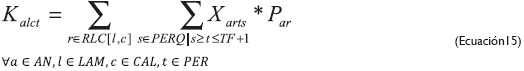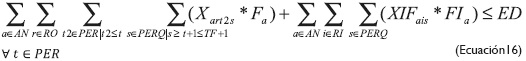Reducción de desperdicios de materia prima en una empresa del sector metalmecánico mediante la implementación y modelación del cutting stock problem^*

Reduction of raw material waste in a metal-mechanic company by the implementation of the cutting stock problem model

Redução de desperdícios de matéria prima numa empresa do setor metalomecânico mediante aimplementação a modelação del cutting stock problem

Juan Pablo Orejuela Cabrera^**, Diana Andrea Pena Calderón^***, Cristiam Andrés Gil González^****

^* Artículo derivado del proyecto de investigación de maestría titulado "Modelación del cutting stock problem en una empresa del sector metal mecánico" realizado en el Grupo de investigación en Logística y Producción y financiado por la Universidad del Valle.
^** MSc. en Ingeniería Industrial. Universidad del Valle, Colombia. Profesor tiempo completo. Escuela de Ingeniería Industrial y Estadística, Cali, Colombia. Investigador principal. Grupo de Investigación: Logística y Producción, e-mail: juan.orejuela@correounivalle.edu.co Autor para correspondencia
^***MSc. en Ingeniería Industrial. Universidad del Valle, Colombia. Co-Investigador. Escuela de ingeniería Industrial y Estadística, Cali, Colombia. e-mail: dianapena86@gmail.com
^**** MSc. en Ingeniería Industrial. Co-investigador. Grupo de Investigación: G3IN, e-mail: crigil@lasallista.edu.co

Artículo recibido: 22/08/2013; Artículo aprobado: 16/06/2014

Resumen

Introducción. Cutting stock problem abarca el tema de cortar grandes rollos de algún material (papel, textil, acero, madera, etc.) en pequeñas tiras de diferentes anchos, que se utilizan como materia prima para la fabricación de un producto final; las longitudes de estas tiras están definidas por los clientes o por las especificaciones del proceso de producción para fabricar el producto final. Objetivo. Desarrollar un modelo matemático que permita la planificación y programación del proceso de corte de rollos de acero, que dé solución a la inquietud: ¿Cómo configurar el corte de rollos satisfaciendo los requerimientos de la demanda y a su vez minimizar los residuos y niveles de inventario en una empresa metalúrgica? Materiales y métodos. Un modelo metodológico fue realizado y aplicado en una planta de producción de tubería en acero, donde se evidenciaban niveles de desperdicio de alrededor de 1,5 % en promedio por rollo cortado. Resultados. Esto, en términos de peso perdido, alcanzaba 25 toneladas por 1700 toneladas que se producen en un mes, lo que hacía que los niveles de inventario de productos en proceso superaran hasta en un 24 % la capacidad de almacenamiento. Conclusiones. El principal resultado de la metodología es la reducción del 4 % del costo semanal de residuos en comparación con el proceso real de la empresa.

Palabras clave: Planeación del inventario, proceso de cortado, programación entera mixta, desperdicio, corte óptimo.

Abstract

Introduction. Cutting stock problem covers the issue of cutting big rolls of any material (paper, fabrics, steel, wood, etc) in small shreds with different widths that, can, then, be used as the raw materials to elaborate a final product. The lengths of these shreds are defined by the clients or according to the specific conditions required by the production process. Objective. Developing a mathematical model that allows the planning and the programming of a cutting process for steel rolls in order to solve the question "how to configure the cutting of rolls satisfying the requirements of the demand and simultaneously minimize the remains and the inventory levels in a metallurgic company? Materials and methods. A methodological model was made and applied in a production plant in which Steel pipes are made. Waste levels of about 15 % per cut roll were found in the place. Results. This, under lost weight terms, reached up to 25 tons per 1700 tons produced in a month, thus making the inventory levels of in process products to be exceeded by up to 24 % of the storage capacity. Conclusions. The main result of the methodology is a 4 % reduction of the weekly cost of waste, compared to the real process of the company.

Key words: Inventory planning, cutting process, mixed integer programming, waste, optimal cut.

Resumo

Introdução. Cutting stock problem abarca o tema de cortar grandes rolos de algum material (papel, têxtil, aço, madeira, etc.) em pequeñas tiras de diferentes largos, que se utilizam como matéria prima para a fabricação de um produto final; as longitudes destas tiras estão definidas pelos clientes ou pelas especificações do processo de produção para fabricar o produto final. Objetivo. Desenvolver um modelo matemático que permita o planejamento e programação do processo de corte de rolos de aço, que dê solução à inquietude: Como configurar o corte de rolos satisfazendo os requerimentos da demanda e a sua vez minimizar os resíduos e níveis de inventário numa empresa metalúrgica? Materiais e métodos. Um modelo metodológico foi realizado e aplicado numa planta de produção de tubagem em aço, onde se evidenciavam níveis de desperdício de arredor de 1,5 % em média por rolo cortado. Resultados. Isto, em termos de peso perdido, atingia 25 toneladas por 1700 toneladas que se produzem num mês, o que fazia que os níveis de inventário de produtos em processo superassem até num 24 % a capacidade de armazenamento. Conclusões. O principal resultado da metodologia é a redução do 4 % do custo semanal de resíduos em comparação com o processo real da empresa.

Palavras importantes: planejamento do inventário, processo de cortado, programação inteira mista, desperdício, corte ótimo.

Introducción

The Cutting Stock Problem consiste en encontrar el mínimo número de unidades de materia prima que se necesitan para obtener un conjunto de ítems de diferentes tamaños. Cada uno de estos ítems tiene una demanda específica, la cual corresponde al número de veces que se va a cortar de las unidades de materia prima, buscando así la minimización del desperdicio (Clautiaux y otros, 2010).

Según Gracia (2010) consiste en satisfacer las demandas de unas determinadas piezas que se deben obtener mediante el corte o partición de un objeto más grande disponible en inventario en unas determinadas cantidades. La asignación generalmente se realiza persiguiendo el objetivo de minimizar los recortes o piezas residuales generadas por el corte.

El proceso del corte tiene un gran impacto en los requerimientos totales y sus costos asociados, por lo cual se hace necesaria la generación de un plan de corte que sea efectivo en términos del costo, pues no solamente se debe buscar minimizar el desperdicio de material sino que este, a su vez, se vea traducido en ahorros significativos para las empresas, dado que los costos asociados a los niveles de inventario de materia prima y de producto en proceso son parte importante de los costos totales, para lo cual es indispensable la toma de decisiones en términos de los niveles de inventario y, a su vez, de un plan de corte óptimo (Abbasi y Sahir, 2010).

Por lo tanto, dado que el Cutting Stock Problem es un problema de optimización, más específicamente de programación lineal entera, para este se puede obtener una solución óptima con resultados económicos y ambientales significativos, si entre sus objetivos se considera alguno de los siguientes:

• Maximizar la utilización del material en inventario (minimizar la cantidad de material en inventario para una lista de materiales dada).

• Minimizar el número de cortes, es decir, mejorar la eficiencia o productividad reduciendo los tiempos de alistamiento.

• Minimizar el desperdicio.

• Mejoramiento de la rentabilidad a través de la reducción del costo de producción y del costo de inventario (nivel de inventario apropiado), o el aumento de los precios de los productos, cumpliendo con los requerimientos de los clientes y las restricciones técnicas que puedan existir.

Dado el gran impacto del proceso de corte en las ganancias de una empresa, el papel que juega el departamento de corte en los sistemas de manufactura tales como la industria papelera, textil, maderera, metalmecánica (Dutta y otros, 2001), entre otras, cobra gran importancia, no solo porque busca la optimización de los recursos disponibles tanto desde el punto de vista económico como ambiental (eliminación y manejo de residuos), sino también por la necesidad de una planeación y configuración de corte adecuada, que tenga en cuenta los requerimientos de demanda, el inventario de materia prima y de producto terminado, y las condiciones inherentes al proceso.

Varios autores como Kantorovich (1939), Gilmore y Gomory (1963), Dyckhoff (1990) han abordado The Cutting stock problem y lo han clasificado, de acuerdo con su grado de complejidad, como un problema NP-hard, debido a que el espacio de búsqueda de soluciones llega a ser muy complejo por las condiciones y restricciones que puede llegar a involucrar, en especial las diferentes combinaciones de corte existentes en el entorno que se estudie (Wongprakornku y Charnsetikul, 2010). Respecto a esto, muchos autores presentan diferentes estrategias de solución tales como heurísticas (Yamase y otros, 2006; Yamase y otros, 2007), metaheurísticas y algoritmos (Cui y otros, 2009). Sin embargo, no existe un enfoque integral para resolverlo (Karelahti, 2002).

La complejidad del sistema se ve afectada por el tipo de asignación, la gama de objetos e ítems, y su dimensionalidad. Con respecto a la última característica mencionada, se considera la más importante, ya que se refiere al número mínimo de dimensiones relevantes para la determinación de la solución, por ejemplo, longitud, ancho, peso, entre otros.

El caso estudio empleado es un problema conocido como de 1.5 dimensiones porque no solo depende del ancho y longitud de las tiras a cortar de los rollos metálicos, sino que estas dimensiones, a su vez, condicionan el peso del ítem resultante. El presente trabajo involucra dos factores importantes que en la literatura consultada no son considerados, y usualmente son establecidos como políticas de la empresa, tales como: todos los rollos deben ser cortados en su totalidad, y las tiras producidas deben ser consumidas para evitar generar inventarios de "remanentes".

En esta propuesta de investigación se desarrolló un modelo matemático que permite el proceso de planificación y la programación de rollos de acero cortado, y responde las siguientes inquietudes:

• ¿Cuántos rollos y cuáles deben ser cortados?

• ¿Cuántas tiras de cada ancho deben ser cortadas por rollo?

Conocer estos dos elementos permite dar solución a la pregunta de investigación: ¿Cómo configurar el corte de rollos con el fin de satisfacer los requerimientos de la demanda y, a su vez, minimizar los desperdicios y niveles de inventario en una empresa del sector metalúrgico?

Materiales y métodos

Fue desarrollado un modelo matemático en lenguaje de programación AMPL, y se empleó como herramienta computacional el solucionador de modelos de programación lineal entera mixta Gurobi del NEOS Server for Optimization. El tiempo de solución fue de alrededor de los 30 minutos. Un tiempo eficiente, teniendo en cuenta que el modelo es muy útil para la toma de decisiones importantes a mediano plazo.

El modelo resultante tiene 4434 variables, de las cuales 764 son binarias, 3024 enteras y 646 lineales, y 2042 restricciones. Esto, al considerar 47 rollos, 16 rollos iniciales, 7 anchos de fleje, 4 tipos de lámina y 3 calibres para un horizonte de tiempo de 5 períodos.

Propuesta metodológica

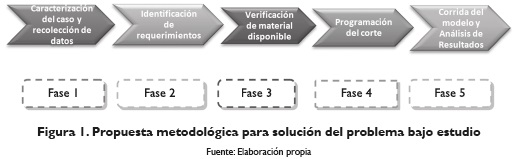
Para abordar el problema del corte en la empresa de sector metalmecánico, se ha realizado una propuesta metodológica que consta de 5 fases, tal como se muestra en la figura 1:

Caracterización del caso estudio y recolección de datos

La empresa tomada como caso de estudio es una organización colombiana fundada el 31 de mayo de 1958, que atiende los sectores de transporte, textil, servicios públicos y metalmecánica.

En este proyecto se plantea como caso de estudio el problema real del corte de rollos de lámina en una planta de producción de tubería en acero ubicada en Yumbo, Valle del Cauca. Desde 1975 fabrica y comercializa tubería metálica con costura y perfilería, donde el proceso de fabricación está distribuido en dos plantas. En la planta 1 se produce tubería de formas redondas, cuadradas, rectangulares, ovaladas y elípticas, en diferentes tipos o calidades de lámina como lo son Cold Rolled (CR), Hot Rolled (HR), Estructural (EH) y Galvanizada (GV) que van desde 7/8" hasta 3" en calibres de 0.70 mm hasta 3 mm. Por otro lado, en la planta 2 se produce todo lo relacionado con perfilería como lo son los ángulos, viguetas, parales, canales, entre otros, en lámina galvanizada (GV) y la tubería de dimensiones pequeñas (Redondos desde 3/8" hasta 7/8" y cuadrados de W) en lámina Cold Rolled (CR) en calibres desde 0.40 mm hasta 1.5 mm.

La planta 1 cuenta con una máquina cortadora de rollos de lámina (Slitter) la cual abastece material de producto en proceso (flejes) para el proceso de producción de tuberías, tanto a la planta 1 como a la planta 2; es decir, que desde la planta 1, que está ubicada en Yumbo, Valle del Cauca, se hacen despachos de flejes hacia la planta 2, la cual se encuentra ubicada en Caloto, Cauca.

Lo anterior quiere decir que la máquina Slitter debe satisfacer los requerimientos de demanda, tanto de la planta 1 como de la planta 2, las cuales tienen niveles de producción mensuales de 1200 t y 500 t en promedio, respectivamente.

Tanto la tubería como la perfilería son fabricadas a partir de rollos de lámina de acero, cortada en flejes (rollos más pequeños), que posteriormente son sometidos al proceso de formado, introduciendo la lámina por una serie de rodillos, donde sus bordes son fusionados en un proceso especial de soldadura por inducción de alta frecuencia, formando así la tubería.

Por lo tanto, cada tipo de tubería a fabricar tiene un ancho de fleje de lámina correspondiente, que permite la fabricación del producto final, es decir, que dependiendo del diámetro del tubo, asimismo debe ser el ancho del fleje que se debe cortar, para lo cual se tienen especificados los anchos correspondientes para cada referencia de tubería, según el tipo de lámina y calibre.

Identificación de los requerimientos

Es necesario identificar el comportamiento de los requerimientos de demanda, para lo cual se debe realizar una clasificación de estos según el tipo de material y las especificaciones o medidas solicitadas, que permita evaluar la disponibilidad del material en términos de los requerimientos y, a su vez, ajustarlos a las restricciones que puedan existir y/o afectar su cumplimiento en el sistema bajo estudio.

En el caso de estudio, se identificaron los requerimientos de demanda para 7 anchos de fleje, 4 tipos de lámina y 3 tipos de calibre en un horizonte de tiempo de una semana (5 días laborales), pues el proceso de corte hace parte de la planeación detallada, es decir, que la planeación es de corto plazo.

Estos requerimientos vienen dados en unidades de peso (kilogramos) para cada ancho de fleje solicitado y su correspondiente tipo de lámina y calibre en un período de tiempo dado, los cuales se encuentran relacionados posteriormente en los parámetros del modelo.

Verificación del material disponible

Esta fase se enfoca hacia la verificación y validación del material disponible en inventario, ya sea de materia prima, producto en proceso y/o producto terminado, lo cual permite tanto la selección de la materia prima que más se ajuste a los requerimientos como la comparación entre el material disponible y el material solicitado, para así actualizar y generar los nuevos requerimientos al considerar el material con el que se cuenta en inventario.

Esta información es de vital importancia, por cual se requiere que sea confiable, veraz y suministrada en tiempo real. En cuanto a la verificación de material disponible en el caso, se consideró tanto la materia prima (rollos) disponible para su corte posterior como el inventario de material ya cortado (flejes) según su ancho, tipo de lámina y calibre.

Para el caso de los rollos, cada uno de estos tiene asociado un período de liberación o llegada, es decir, el período en el cual ya se puede disponer de ellos para su corte. Para el caso de estudio se consideraron 47 rollos de lámina. Este material disponible viene dado en unidades de peso kilogramos y, a su vez, tiene asociado un ancho en milímetros.

En cuanto a los flejes, se definieron 16 rollos iniciales de los cuales provienen unos flejes iniciales de cada ancho, tipo de lámina y calibre, y se encuentran disponibles al inicio del horizonte de tiempo, es decir, el inventario inicial disponible para cumplir los requerimientos. Este material viene dado tanto en unidades de fleje como en unidades de peso, para así garantizar que el consumo sea entero.

Al comparar el material total disponible con los requerimientos de demanda se observó que hay existencia suficiente tanto en rollos como en flejes para dar cumplimiento a estos requerimientos; por lo tanto, se debe encontrar una configuración óptima de corte que permita aprovechar de la mejor forma posible el material del que se dispone, es decir, optimizar los recursos con los que se cuenta, desperdiciando lo menos posible.

Programación de corte

Una vez se han identificado los requerimientos y se han cruzado con el inventario, es necesario definir el patrón o configuración de corte asociado a cada material, de forma que se encuentre el mínimo número de unidades de materia prima que se necesitan para obtener un conjunto de ítems de diferentes tamaños que satisfagan los requerimientos de demanda, pues un programa de corte se compone de un conjunto de decisiones relacionadas entre sí, como lo son:

• Selección de la materia prima a cortar.

• Asignación de la materia prima a cada demanda específica.

• Construcción del patrón de corte para cada materia prima a cortar.

Para la programación del corte mediante el modelo de programación lineal entera mixta, se deben tener en cuenta los siguientes parámetros:

• Se consideran 5 períodos de tiempo para realizar la programación del corte.

• El número de rollos r disponibles para corte es de 47, donde cada rollo está asignado a un tipo de lámina y calibre, y el número de rollos iniciales i es de 16 rollos.

• Los anchos de los rollos A_r son de 1219 mm y 1000 mm, y los anchos de los flejes requeridos F_r y F son 7 de las siguientes medidas: 152 mm, 73 mm, 79 mm, 58 mm, 228 mm, 38 mm y 67 mm.

• Los requerimientos de demanda R_als vienen dados en Kg para 7 anchos de flejes, 4 tipos de lámina y 3 calibres.

• Cada rollo tiene un ancho y un peso asociado, y cada fleje tiene su peso respectivo dependiendo de su ancho, y del peso y ancho del rollo del que provengan. El peso se encuentra en kilogramos, y el ancho, en milímetros.

• Cada rollo debe tener un desperdicio mínimo DM_c según el tipo de lámina y calibre.

• El desperdicio máximo (DMX) independientemente del tipo de lámina y calibre es de 15 mm.

• Para el cumplimiento de los requerimientos, se ha definido que los despachos se pueden encontrar por debajo del requerimiento en un 5 % (DESVI) y por encima en un 15 % (DESVS).

• Para el corte de los rollos se considera un número máximo de flejes por rollo FR_Cc dependiendo del tipo de lámina y calibre.

• El espacio de almacenamiento disponible ED es de 100 000 mm lineales.

Modelo de programación de corte

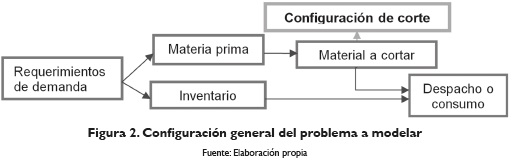
En la figura 2 se describe la configuración general del modelo desarrollado:

Conjuntos

RO = Conjunto de rollos

RI = Conjunto de rollos iniciales

AN = Conjunto de anchos de banda de fleje

LAM = Conjunto de tipo de lámina

CAL = Conjunto de calibres

RLC [l,c] = Conjunto inducido que representa los rollos que pertenecen a un tipo de lámina y calibre específicos.

ILC [l,c] = Conjunto inducido que representa los rollos iniciales que pertenecen a un tipo de lámina y calibre específicos.

PER = Conjunto de períodos en los cuales son cortados los rollos.

PERQ = Conjunto de períodos en los que se cumplen los requerimientos de la demanda.

Índices

Parámetros

PR_r=Peso del rollo r [kg]

A_r=Ancho del rollo r [mm]

F_a=Magnitud de los flejes de ancho a [mm]

FI_a=Magnitud de los flejes iniciales de ancho a [mm]

P_ar= Peso de un fleje de ancho a proveniente del rollo r [kg]

R_alcs= Kilogramos requeridos de flejes de ancho a de tipo de lámina l de calibre c en el período s [kg]

DM_lc= Desperdicio mínimo del tipo de lámina l de calibre c [mm]

DMX=Desperdicio máximo [mm]

FR_lc=Cantidad máxima de flejes a cortar dependiendo del tipo de lámina l y calibre c [unid.]

DESVI=Desviación mínima entre el requerimiento y el despacho [%]

DESVS=Desviación máxima entre el requerimiento y el despacho [%]

TF=Período final del horizonte de tiempo [unid.]

PL_r=Período de liberación del rollo r [unid.]

INI_ai=Número de flejes iniciales de ancho a provenientes del rollo inicial i [unid.]

PI_ai= Peso de un fleje de ancho a proveniente del rollo inicial i [kg]

CD_r= Costo de desperdicio del rollo r [$/mm]

CI_ai=Costo de mantener en inventario de flejes de ancho a provenientes del rollo inicial i [$/kg]

CIR_ar= Costo de mantener en inventario de flejes de ancho a provenientes del rollo r [$/kg]

ED= Espacio de almacenamiento disponible en la bodega [mm lineales]

Variables

X_arts= Número de flejes del ancho a, a cortar del rollo r en el período t para cumplir con el requerimiento en el período s; s>=t [unid.]

XI_ais=Número de flejes de ancho a provenientes del rollo inicial i a utilizar del inventario inicial para cumplir con el requerimiento en el período s (unid.]

XIF_ais=Número de flejes de ancho a provenientes del rollo inicial i que quedan del inventario inicial a utilizar para cumplir con el requerimiento en el período s [unid.]

K_alct= Kg. Cortados de flejes de ancho a de tipo de lámina l de calibre c en el período t [kg] (Variable de consolidación)

D_alcs=Despacho de flejes de ancho a de tipo de lámina l de calibre c en el período s. [kg]

IFP_alcs= Inventario final de los flejes de ancho a de tipo de lámina l de calibre c en el período s [kg]

Función objetivo

Restricciones

El propósito de la función objetivo (ecuación 1) es minimizar los costos en los que se incurre durante el proceso del corte de objetos (rollos) para generar ítems (flejes), los cuales son básicamente los costos asociados al desperdicio generado, el nivel de inventario inicial a mantener y el nivel de inventario según su tiempo de permanencia. La ecuación 2 define que los despachos de los flejes según su ancho, tipo de lámina y calibre para cada período deben ser iguales al inventario inicial, más el material cortado al inicio del período.

Las ecuaciones 3 y 4 son las políticas de cumplimiento de la demanda; estas son definidas por la empresa y permiten que exista una flexibilidad en el proceso, disminuyendo complejidad computacional del modelo y generando mejores resultados. Las ecuaciones 5 y 6 son de gran importancia, ya que garantizan que el inventario inicial de los flejes no se despache o consuma parcialmente para ajustarse a los requerimientos, sino que sea de forma entera o completa.

La ecuación 7 busca que el material que no se despache en ningún período del horizonte de tiempo corresponda al inventario final IFP_alc, así asignando el material que sea cortado y que supere los requerimientos totales. Las ecuaciones 8 y 9 definen que los rollos de material pueden solo ser cortados si están disponibles en inventario.

Las ecuaciones 10 y 11 corresponden al rango de desperdicio que puede existir entre el cortado de patrones y el rollo total. También es una política de la empresa y muchas veces está supeditada a los requerimientos de la maquinaria al manejar el material.

Mediante la ecuación 12 se pretende que un fleje se genere solo si el rollo se corta, pues los flejes provienen de los rollos y, a su vez, define un límite máximo de cortes por rollo, ya que dependiendo del tipo de lámina (propiedades mecánicas) y su calibre, el número de flejes puede afectar el desempeño de la máquina, debido al esfuerzo que debe hacer esta durante el corte. Se plantean dos restricciones (ecuaciones 13 y 14) para limitar la cantidad a cortar por rollo. La primera considera el límite de cantidad a cortar en términos del peso de cada uno de los rollos, es decir, que no se puede cortar más de lo que pesa el rollo; y la segunda define el límite de cantidad a cortar en términos del ancho del rollo.

La restricción de la ecuación 15 se estableció para consolidar en una sola variable (K_altc) la cantidad de material cortado (X_arts) en términos de peso (P_ar), y así comparar los requerimientos de demanda y validar su cumplimiento. La ecuación 16 establece un límite máximo para la generación de material en inventario en cada período de tiempo teniendo en cuenta el espacio de almacenamiento disponible. La ecuación 17 define la naturaleza de las variables y su no negatividad.

Resultados

Para la aplicación del modelo de programación lineal propuesto a la instancia final se consideraron 47 rollos, 16 rollos iniciales, 7 anchos de fleje, 4 tipos de lámina y 3 calibres para 5 períodos de tiempo, tal como se mencionó anteriormente. Para este problema, se encontró una programación óptima en la cual resultó que se cortaron 42 rollos de los 47 disponibles con sus respectivas configuraciones de corte para cumplir los requerimientos de demanda y, además, se observa que los rollos que se cortaron solo fueron cortados una vez a lo largo del horizonte de tiempo.

Los rollos fueron cortados teniendo en cuenta su período de disponibilidad o liberación, y los costos incurridos al cortarlos como son los de desperdicio CD y de mantener inventario CIR_ar. Por ejemplo, de los rollos de lámina CR y calibre Cl disponibles no se cortaron dos (R3 y R4), pues eran lo más costosos en términos del desperdicio y del inventario, tal como se muestra en las tablas 1 y 2:

En cuanto al costo de mantener en inventario los flejes provenientes de los rollos R3 y R4, estos eran los más costosos ($1355/kg y $1350/ kg, respectivamente), pues son los más pesados, y como el costo de mantener viene dado por cada kg cortado, se ve reflejado como un costo mayor en la función objetivo con relación a los flejes provenientes de los otros rollos del mismo tipo de lámina y calibre:

Por lo tanto, el modelo busca cumplir con cuatro condiciones para el corte de los rollos:

• Que el rollo se encuentre disponible en el período para su corte.

• Que cumpla con el peso necesario para cumplir con los requerimientos de demanda.

• Que sea el menos costoso en términos del desperdicio y del inventario.

• Que no se haya cortado en un período anterior.

En cuanto a la función objetivo, se observa que la estructura de costos se encuentra distribuida de la forma en que muestra en la tabla 3:

Análisis de sensibilidad

Para conocer el comportamiento del modelo de programación lineal propuesto, se realizaron análisis en términos de la sensibilidad, variando los parámetros que más afectan los resultados del modelo.

En el caso de la desviación entre el material requerido y el despachado, se encontró que en el problema que se aplicó como caso de estudio, todo lo despachado en cada período de tiempo para cada tipo de lámina y calibre estuvo dentro del rango establecido de 5 %-15 %.

Pero cuando se realizaron variaciones con valores que se encuentran por debajo de los de la instancia inicial generan infactibilidad; por lo tanto, la desviación de los requerimientos (DESVI y DESVS) es uno de los elementos que más afecta la factibilidad del modelo. Inicialmente se modificó el límite inferior para conocer su comportamiento (tabla 4):

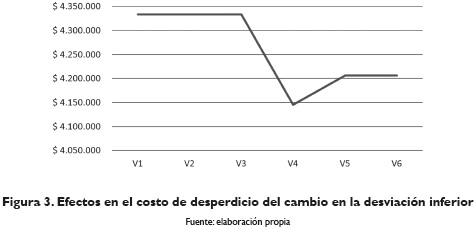
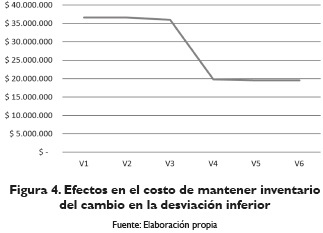
Con estas variaciones al límite inferior se observó una disminución del costo de desperdicio y de mantener en inventario flejes cortados, pues con una menor desviación se incrementa la probabilidad de que de un rollo se puedan cortar más flejes, es decir, mayores opciones para combinar las configuraciones de corte, generando así un menor desperdicio, tal como se muestran en las figuras 3 y 4. Por otro lado, se disminuye el nivel de inventario, pues al reducir el límite inferior de las desviaciones la demanda "disminuye"; por lo tanto es necesario cortar menos flejes.

En cuanto a las variaciones de la desviación por el límite superior, se realizaron las siguientes versiones (tabla 5):

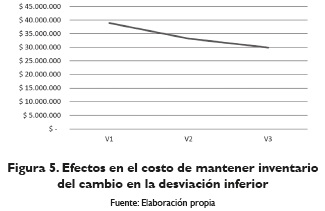
Durante la implementación, las tres últimas versiones no corrieron, pues superaban la capacidad del Neos Server; por lo tanto, se presenta el comportamiento de las tres primeras versiones, en donde se observa una tendencia de disminución del costo de mantener en inventario flejes cortados (figura 5), debido a que a mayor demanda se puede despachar más material y tener menos en inventario.

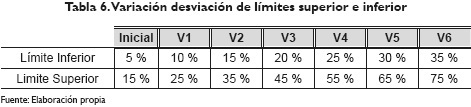
Posteriormente, se realizaron versiones aumentando los dos límites de la desviación de los requerimientos, tal como se muestra en la tabla 6:

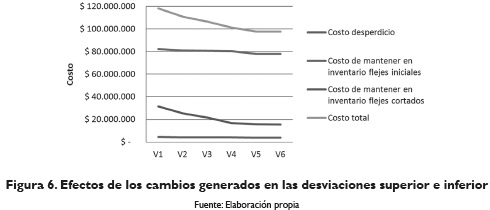
Al llevar a cabo estas variaciones al parámetro de desviación, el modelo se inclina hacia el límite inferior en vez al superior, por la naturaleza del modelo que es de minimización de costos; se logra así que se corte menos material, pues de la versión inicial a la versión 6 se deja de cortar un rollo al pasar de 42 rollos a 41, lo cual se ve reflejado en una disminución de los costos totales, tal como se muestra en la figura 6.

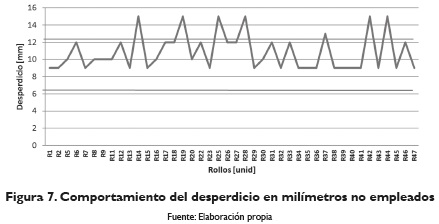
En cuanto al nivel de desperdicio, en la instancia final se consideró que el límite inferior estaba entre los 8 y 9 mm dependiendo del tipo de lámina y del calibre, y el límite superior era de 15 mm, tal como se muestra en la figura 7.

Se revisaron los casos en los cuales el desperdicio se encontró en los dos puntos extremos: 9 mm y 15 mm, y se observó que las configuraciones de corte se encontraban balanceadas en términos de los anchos de los flejes, es decir, que estaban conformadas tanto por flejes anchos como angostos, pues no se encontraron configuraciones en las que todos los flejes fueran angostos o todos anchos, ya que por lo general los flejes angostos son esenciales para completar el ancho del rollo y así poder obtener un desperdicio dentro de los rangos especificados.

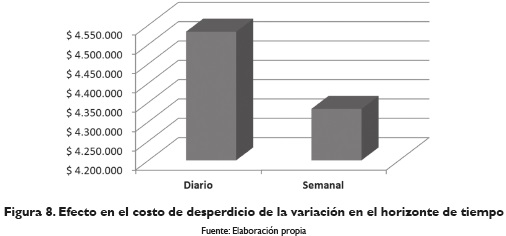
Por otro lado, se evalúa el proceso de planeación detallada, ya que actualmente la empresa realiza el proceso de construcción de los patrones de corte diariamente, debido a la forma en la que están establecidos los programas de producción de las plantas y la programación de los despachos a la planta 2. En el modelo, el horizonte de planeación fue de una semana (5 días laborales) y se comparó con el proceso real de la empresa, que es la programación diaria, para lo cual se construyeron 5 modelos para cada día y se obtuvo que en términos del costo es más recomendable realizar la programación con un horizonte de tiempo más grande, pues se tienen mayores opciones para combinar y conformar los patrones de corte, logrando así obtener mejores combinaciones en términos del nivel de desperdicio total, tal como se muestra en la figura 8. Este cambio en el horizonte de planeación representa una reducción del 4 % semanal del costo de desperdicio.

Conclusiones

El desarrollo de este trabajo de investigación aporta una propuesta metodológica que permite dar solución a este tipo de problemas considerando los requerimientos de demanda, el material disponible en inventario, y la configuración de patrón de corte. Esta propuesta permite identificar los requerimientos y la disponibilidad de material para darles cumplimiento a estos, ajustándose a ellos mediante el modelo programación lineal, propuesto para la programación del corte.

Este modelo no solo considera la configuración de los patrones de corte sino que incluye la verificación del material disponible en inventario, tanto en materia prima como en producto en proceso, el espacio de almacenamiento disponible, los niveles de cumplimiento de los requerimientos (desviaciones), las restricciones de la máquina y el material a cortar como lo es el número de cortes y niveles de desperdicio, y los costos de desperdicio y de mantener en inventario producto en proceso, entre otros. Adicionalmente, cabe resaltar que el modelo fue implementado en un sector real de la industria como lo es el metalmecánico, teniendo en cuenta las necesidades implicadas en este sector, y los datos fueron obtenidos de la misma.

En cuanto a la implementación del modelo propuesto, se observó que su complejidad radica en que los datos de entrada (requerimientos de demanda) son de tipo de continuo y los datos de salida (número de flejes a cortar) deben ser de tipo entero, por la condición que existe de que los flejes deben despacharse o consumirse en su totalidad y no parcialmente, y que deben ajustarse lo más cercano posible a los requerimientos, para lo cual se establecieron unos límites de incumplimiento o desviación por encima y por debajo de los requerimientos. Se evidenció que esta desviación afecta en gran medida la factibilidad del modelo, así como el nivel de inventario con el que se cuenta, pues entre más cercano se necesite lo que se despacha con relación al requerimiento, se evidencia una mayor complejidad para resolverlo, lo que afecta su la factibilidad.

Conjuntamente, no se consideró tanto el largo como el ancho como tradicionalmente numerosas investigaciones lo han abordado, sino que se tuvo en cuenta el ancho tanto en los flejes requeridos como en los rollos disponibles para cumplir con los requerimientos de demanda, sin considerar el largo, debido a que los requerimientos de demanda están dados en términos del peso necesario que deben tener los flejes para cumplir con las diferentes necesidades.

Con relación a la metodología de solución y a la herramienta computacional empleada, el tiempo de solución del modelo varía dependiendo del tamaño de la instancia y del nivel de cercanía del material despachado con relación al requerido, pues entre más cercano se requiera lo que se despache o se consuma, más compleja es la búsqueda de la solución óptima y, por ende, el tiempo de solución aumenta. Para la instancia final implementada el tiempo de solución fue aceptable a pesar de ser un modelo de programación lineal de alta complejidad.

En el caso de instancias más grandes o de un horizonte de tiempo más extenso valdría la pena explorar otras metodologías de solución para investigaciones futuras como las metaheurísticas; para el caso de estudio aplicado la metodología de solución utilizada fue la adecuada, pues en la empresa metalmecánica estudiada la planeación y la programación del corte se hacen día a día, es decir, que los horizontes de tiempo son cortos.

Por lo tanto, se plantea como recomendación para la empresa realizar la programación con un horizonte de tiempo más grande pues se tienen mayores opciones para combinar y conformar los patrones de corte, lo cual genera una reducción en los costos totales.

Referencias bibliográficas

Abbasi, J. A. & Sahir, M. H. (2010). Development of Optimal Cutting Plan using Linear Programming Tools and MATLAB Algorithm. International Journal of Innovation, Management and Technology, 1(5), 483-492.         [ Links ]

Clautiaux, F.; Alves, C.; De Carvalho, J.V. & Rietz, J. (2010). New stabilization procedures for the cutting stock problem. INFORMS Journal on Computing, 23, 530-545.         [ Links ]

Cui, Y. & Lu, Y (2009). Heuristic algorithm for a cuttings rock problem in the Steel bridge construction. Computers & Operations Research. 36: 612-622        [ Links ]

Dyckhoff, H. (1990). A typology of cutting and packing problems. European Journal of Operational Research, 44, 145-159.         [ Links ]

Gilmore, P. & Gomory, R. (1963). A linear programming approach to the Cutting Stock Problem-Part II. Operations Research, 11(6), 863-888.         [ Links ]

Gracia, C. P. (2010). Métodos y algoritmos para resolver problemas de corte unidimensional en entornos realistas. Aplicación a una empresa del Sector Siderúrgico. Valencia, España: Departamento de Organización de Empresas. Universitat Politécnica Valéncia.         [ Links ]

Dutta, G. & Fourer, R. (2001). A survey of mathematical programming applications in integrated Steel plants. Manufacturing & Service Operations Management, 4, 387-400.         [ Links ]

Kantorovich, L.V. (1960), Mathematical methods of organizing and planning production. Reprinted in Management Science, 6, 366-422.         [ Links ]

Karelahti, J. (2002). Solving the cutting stock problem in the steel industry. Department of Engineering Physics and Mathematics. Helsinki University of Technology, 2-5.         [ Links ]

Wongprakornkul, S. & Charnsethikul, P. (2010). Solving One-Dimensional Cutting Stock Problem with Discrete Demands and Capacitated Planning Objective. Journal of Mathematics and Statistics, 6, 79-83.         [ Links ]

Yanasse H. H. & Lamosa Pinto, M. (2007). An integrated cutting stock and sequencing problem. European Journal of Operational research, 183(3):1353-1370.         [ Links ]

Yanasse, H. H. & Limeira, M. S. (2006). A hybrid heuristic to reduce the number of different patterns in cutting stock problems. Computers & Operations Research, 33(9): 2744-2756.         [ Links ]