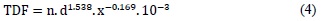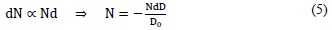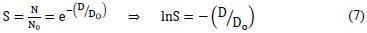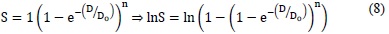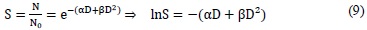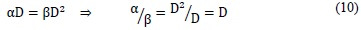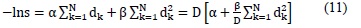DOI: http://dx.doi.org/10.18180/tecciencia.2014.17.2

Evolution of Physico-Mathematical Models in Radiobiology and their Application in Ionizing Radiation Therapies

Evolución de los modelos fisicomatemáticos en radiobiología y sus aplicaciones en terapias de radiación ionizada

O. Garzón¹, M.C. Plazas², E. J. Salazar³

¹ Universidad Nacional de Colombia, Bogotá, Colombia, Oggarzono@unal.edu.co
² Universidad Nacional de Colombia, Bogotá, Colombia
³ Universidad Nacional de Colombia, Bogotá, Colombia

How to cite: Garzón, O. M. et al., Evolution of physic-mathematical models in radiobiology and their application in ionizing radiation therapies, TECCIENCIA, Vol. 9 No. 17., 15-22, 2014, DOI: http://dx.doi.org/10.18180/tecciencia.2014.17.2

Received: 10/Aug/2014 Accepted: 15/Sep/2014 Published 30/Dec/2014

Abstract

Radiobiology is the science of studying the interaction between radiation and biological tissues and the effects of the first on the latter. In this paper, we present various Physico-Mathematical models used in Radiobiology, which have been developed in order to compare and quantify the effectiveness of different radiation regimens. Different researchers have developed empirical models based on experimental considerations and on a radiological foundation. In one application of ionizing radiation therapies, the studies were able to relate several important parameters, such as dose per fraction, total dose, and the treatment time needed to obtain a better therapeutic index. In this paper, we aim to describe and discuss a number of radiobiological aspects of the results obtained throughout past research, such as Isoeffect Curves, Nominal Standard Dose (NDS), time-dose fractionation factors (TDF), and cell survival curves. Finally, we analyze the Linear-Quadratic Model.

Keywords: Isoeffect, Dose Fractionation, sub-lethal damage, lethal damage, cell survival, linear quadratic model.

Resumen

La radiobiología es la ciencia encargada del estudio de la interacción de la radiación con los tejidos biológicos y de los efectos producidos sobre ellos. En este trabajo se presentan algunos modelos Físico-Matemáticos en Radiobiología, que se han desarrollado para la comparación y cuantificación de la efectividad de diferentes regímenes de radiación. Diferentes investigadores han logrado desarrollar modelos empíricos, basados en consideraciones experimentales y modelos a partir de bases radiológicas. En una aplicación a las terapias con radiaciones ionizantes, los estudios logran relacionar varios parámetros importantes tales como dosis por fracción, dosis total y el tiempo del tratamiento para obtener un mejor índice terapéutico. En este trabajo, se pretende describir y discutir algunos aspectos radiobiológicos, de los resultados obtenidos en todo su desarrollo, tales como: Curvas de Iso-efecto, Dosis Nominal Estándar (NDS), Factor Dosis-Tiempo de Fraccionamiento (TDF), Curvas de supervivencia Celular y finalmente se analiza el Modelo Lineal Cuadrático.

Palabras clave: Isoefecto, Dosis, Fraccionamiento, Daños Sub-Letales, Daños-Letales, Sobrevida Celular, Modelo Lineal Cuadrático.

1. Introduction

A variety of radiobiological studies and models were developed during the first decades on the 20th century. These served as a basis for research on cancer treatment with ionizing radiations (radiotherapy). This paper seeks to approach the conceptual and physico-mathematical development of radiobiological models. We present the parameters that model cellular response in interaction with ionizing radiation. Initially, we establish some generalities about biological cellular components and their vulnerability to physical, chemical and biological effects induced by ionizing radiation. We examine the relationship between the microenvironment of cell growth (both healthy tissues and cancerous tumors), time-dose fractionation factors (TDF) and biological responses.

Subsequently, the evolution of several empirical models is shown. These are based on experimental curves, called Isoeffect Curves, which determine the relation between the biological effect and the total administered dose. After-wards, we discuss models that propose the cell as a single target or as a multi-target which can interact directly with the ionizing radiation. These models flow into the Linear Quadratic Model which attempts to mathematically model the experimental behavior of the cell survival curves.

These so-called curves show the relationships between total dose, dose per fraction total treatment time, and the influence of the ionizing radiation energy linear transference. These physical parameters are associated with biological parameters, such as α and β coefficients, which measure the degree of damage caused by ionizing radiation on cells. The damages are classified as sub-lethal or lethal, according to the Linear Quadratic Model.

Cancer morbidity is rising each year, influenced by different environment and cultural factors, as well as by the in-crease in longevity. Radiobiology, along with technological development, will continue to find solutions to improve the techniques and protocols of treatments, with the aim of maintaining radiotherapy as one of the most effective cancer treatment methods [1]

2. Overview

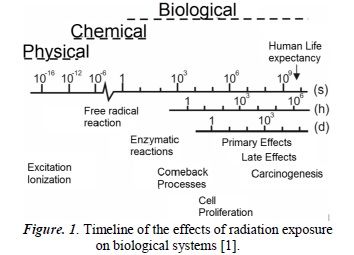
The irradiation of any biological system produces a succession of physical, chemical and biological processes that can be approximated in a wide timeline (See Figure 1). The physical phenomena that take place in the interaction of radiation with the atoms that constitute the cells generate excitation or ionization that destabilize the normal structure of the molecules found therein. For example, a highly energetic electron takes about 10-18s to traverse a molecule of deoxyribonucleic acid DNA [2], creating ruptures in one or both of its helixes.

Now, because the cytoplasm is constituted principally of water, these are the molecules which are mainly affected by radiation. They react chemically inside the cell between themselves and with other cellular constituents, producing highly reactive free radicals which are added to the DNA, altering its chemical constitution. Almost every process taking place in cells requires enzymes that act as catalysts to accelerate these processes and to find balance. Hence, many radio-induced lesions are expected to be successfully mended. Nevertheless, depending on its degree of complexity, the lesion can lead to cellular death or intervene severely in the mitotic cell division cycle. In these biological processes, DNA seeks repair and the cell in its entirety seeks to return to normal function.

The correct functioning of the cell and the optimal performance in the transmission of genetic information depend on the integral maintenance of DNA molecules. The damage caused by free radicals in this molecule is the main cause of radiobiological effects post-irradiation; the repair processes on the DNA can be complete or incomplete. Depending on the complexity of the legion, genetic mutations or loss of reproductive capability can occur, along with other consequences.

Cells can be classified as differentiated or undifferentiated. The former, also called mature cells, execute specific functions in the correct function of the human body; the latter do not execute any functions, but rather only serve as precursors for differentiated cells. According to the law of Bergonié and Tribondeau [2], undifferentiated cells constantly experience mitotic activity, which makes them more radio-sensitive than differentiated cells.

One can infer from this that organs constituted by radio-sensitive cells will be more sensitive to radiation. In fact, this is one of the fundamental principles in radiotherapy - cancer cells are highly proliferative, thus they are in constant mitotic activity, which means they are highly vulnerable to radiation [1] [3]

Tumor growth is characterized by the disproportionate and unorganized growth of the tissue structure; it is, in general, an abnormal growth, with a deficit of blood vessels. Tumorous cells grow in an environment lacking in nutrients and oxygen, which leads to the conformation of heterogeneous tumor regions, called tumor nodules, with different degrees of proliferation and different responses to ionizing radiation therapies.

Healthy tissues and organs are irrigated by blood vessels, which allow in a supply of oxygen and nutrients. This allows for a complete, quicker recovery in the face of cancerous tumors. This is why the temporal influence turns out to be a key factor, since by fractioning the therapeutic radiation dose¹ in time intervals, the healthy tissues and organs will have more capacity to recover in time, which is not the case with cancerous tumors [1] [3]

In therapies using ionizing radiation for the eradication of cancerous tumors there are other important physical factors. Cell damage is proportional to the dose rate. This indicates the dose supply per time unit. The higher the dose rate is, the higher the inhibition of the repairing systems in cells, because there is a higher probability of affecting the cell, particularly the DNA present in their nucleus, meaning more destroyed cells.

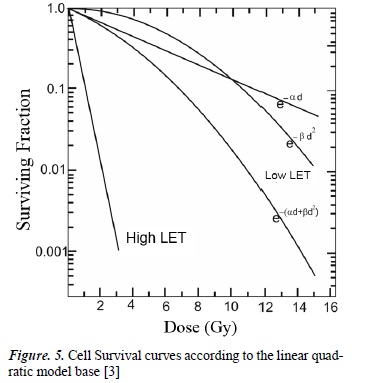
The quality of radiation, determined by linear energy transfer (LET), also indicates the ionizing capacity per unit of length of the radiation when interacting with other materials, in this case biological tissues. For example, charged particles have a high LET compared to photons, which means they generate a large number of excitations and ionizations in the atoms and molecules of cells, causing greater damage in their DNA. This is shown in the cell survival curves (See Figure 5) where cell survival is analyzed according to the dose (for low or high LET radiation) [3]

3. Physico-Mathematical Models

The development of biological concepts and physical parameters that describe the effects of ionizing radiation on various tissues are described below. Their respective experimental fundamentals and the employed mathematical models are also defined.

3.1. Models Based on Empirical Isoeffect

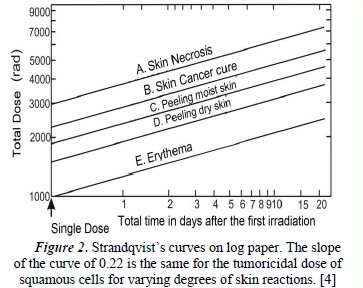
In 1944 Strandqvist [4] developed a new scientific approach to the effects of ionizing radiation, introducing the isoeffect curve (dose-isoeffect), which represents the way the total dose of a fractionated treatment changes, depending on the total treatment time to produce an equivalent isoeffect (see Figure 2). This model is based on the fact that "the total dose in the total time determines the effects, independent of fractionation".

Using a standard treatment scheme (2Gy/day, 5 times per week), and using a 250 kV X-ray machine, Strandqvist carried out experimental measures for the control of cancer effects on the skin. He thus obtained a family of curves (Figure 2), where an optimal region can be found which favors the curing of the tumor with minimal complications [4]

This was expressed as:

Where D is the total dose, T is treatment time, p is a potency less than 1 (to be determined), and k is the constant of proportionality (an interpretation of which will be presented later in this paper). The exponent of T, equivalent to the slope of the Strandqvist curves, represents the average value of the reparation and recovery capacities of normal or tumorous tissues.

Stranqvist demostrated the relationship between the dose and the total treatment time required to produce a certain biological isoeffect. Cohen [5] analyzed and compared the response data of normal tissues, such as skin with skin cancer recurrences, and suggested, in this specific case, that the slope of the isoeffect curve for skin was 0.33 in normal tissues and 0.22 in tumorous tissues. This gave the relationship between tolerance dose and total treatment time.

3.1.1 Nominal Standard Dose (NSD)

In 1967, Ellis [6] proposed a mathematical expression relating total dose, treatment duration time and the number of fractions used in the total dose regimen. According to empirical research performed by Fowler [7] and Stern [8] on normal skin tissue, the isoeffect dose was shown to be not only related with time but also with the number of fractions. This was used by Ellis to replace the term T0,22 with np in expression (1) above, where n is the number of fractions. Ellis uses a standard scheme of 30 fractions of 2 Gy administered over 40 days, which allows him to find the value of the exponent of the number of fractions, using the following relationship:

40²=30^p ⇒ p=0,24

Which turns expression (1) into:

The constant of proportionality k is adjusted to a treatment scheme, assigning it the name NSD, and whose physical interpretation facilitates the comparison of treatments with different fractionation schemes and different total times, indicating the biological effect [9] [10]. The dimensions of this constant include dose and time, and the pro-posed unit is the RET (rad equivalent therapy) [11]. Expression (2) then becomes:

NSD is used to calculate the tolerance of normal tissue in the tumor region and represents the tolerance of normal connective tissue, which is given at 1800 ret [10]

The NSD concept was well received, because it simplified the comparison of treatments. However, it presented various problems:

1. It does not represent a single equivalent dose because the isoeffect time calculated by Ellis used data from 4 to 30 fractions.
2. NSD cannot be calculated when there is no variation in the volume treated or in therapy interruptions.
3. NSD tables are useful for subcutaneous and skin tolerance only, and cannot be applied to tumors or other normal tissues [12]

3.1.2 Time-Dose Fractionation Factor (TDF)

Orton and Ellis introduced the Time-Dose Fractionation Factor (TDF) in 1973 [9] This model relates the effect of two therapeutic schemes using the TDF value, where the effects are the same if the TDF value is the same for both schemes. The TDF value obtained by Otron and Ellis is calculated as a function of time and fractionation. Its mathematical expression is the following:

Where n is the total number of fractions, d is the dose per fraction, and x is the coefficient of proportionality which relates the days of the week with the number of sessions per week. The advantage of this model is the linear behavior of the TDF with respect to n, thus relating different treatment protocols. Additionally, this model is applied easily in clinical practice and relates the fundamental variables of a radi-otherapy treatment: dose, time and number of fractions. However, this model has some disadvantages, such as its short range of applicability on different tissues.

The aforementioned models have been substituted by those deduced from the cell survival equations, including the Linear Quadratic model.

3.2 Models based on Cell Survival Curves and Isoeffect

The interpretation of the effects of radiation on healthy and tumorous tissues has to be made according to the effect caused by the cells that compose these tissues. The survival cells are those that carry out their reproductive activities, along with their functions, after irradiation. Cell death takes place when the cell stops carrying out its function in the differentiated cells, and ceases its reproductive activities in un-differentiated cells.

The methods used in the determination of the cell survival curves exposed to radiation are grouped into two categories: in-vitro and in-vivo. In-vitro methods are based on the ability of some cells to survive and reproduce in a culture medium, whereas in-vivo methods are based on cell counts in certain organs after being irradiated [13]

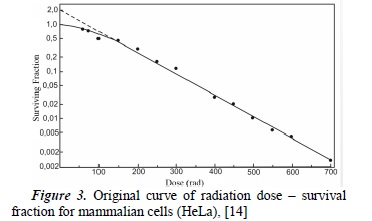
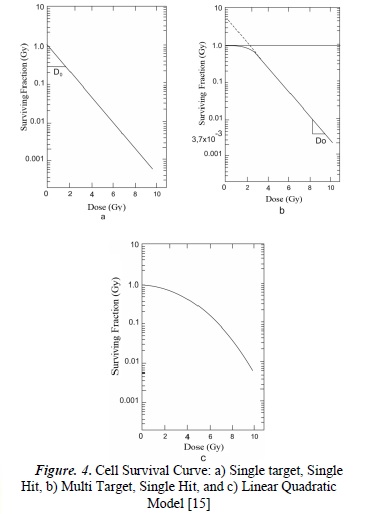
A survival curve is presented in semi-algorithmic form (see Figure 3), with the real dose value on the x-axis, and the natural logarithm of the survival fraction on the y-axis. In accordance with empirically-acquired data, interpolations and extrapolations have been generated in order to obtain cell survival curves. These mathematical procedures, along with their theoretical assumptions, originated a number of survival curve models, such as:

1. Single target - Single Hit Model,

2. Multi target - Single Hit Model,

3. Linear Quadratic Model [13].

3.2.1. Single Target - Single Hit Model

In this model [13] each cell is assumed to contain a single target; the inactivation of this leads to cell death. In addition, a single hit inactivates that single target. Mathematically [10], the number of targets dN inactivated by a small dose dD is proportional to the number of targets N and to the dose dD. Therefore:

Where Do is a constant that corresponds to the value of the dose that permits 37% of cell survival and the minus sign indicates cell death. The value D0 characterizes the intrinsic sensitivity of a cell population. This means the smaller the dose that reduces the original cell population to its 37%, the larger the sensitivity to radiation. Integrating (5), we obtain:

Where No is the initial number of cells and N is the number of cells surviving a dose of radiation.

Considering the cell as a single target, the survival of a cell population is represented by the survival s, and it is expressed as:

Where the value Do can be interpreted as the average dose for a relation of a hit per target.

Expression (7) represents the survival curve for a single target with a single hit. Observing Figure (4a), we can infer linear behavior in a semilogarithmic scale. This model allows the interpretation of survival curves in mammalian cells with very sensitive ratios that correspond to tumorous tissues. It also allows the deduction of the cell response to low dose rates using high LET radiations.

3.2.2. Multi Target - Single Hit Model

In this model [13], the cell is considered to have multiple targets, and the inactivation of all of them is necessary in other to achieve cell death. Each target is inactivated by a single hit. According to the previous interpretation, and according to logical deduction, the survival equation for this model is:

Where S is the fraction of survival, D the total dose, Do is a constant that corresponds to the average dose of a hit per target, therefore maintaining the interpretation of the previous model, and n is the number of targets of the cell.

The survival curve obtained for this model has an initial slope equal to zero, which makes it impossible to correctly model the behavior of the majority of mammalian cells because, empirically, the survival curves generally show an initial negative slope. Nevertheless, as the dose increases, the behavior obtained corresponds to the empirical survival curves.

3.2.3 Linear Quadratic Model of Cell Survival [13]

The Linear Quadratic Model [13] is a mathematical formulation which uses a second-degree polynomial and assumes that each cell is killed because of the inactivation of two or more targets. Therefore, when there is an impact, two possibilities are considered: a) that the cell injury is irreparable, and b) that the injury is reparable by the cell itself. The interpretation of this in relation to the cell survival curve is that the curve is determined through two components, one linear (proportional to the radiation dose, related to the irreparable injury), and the other proportional to the square of the radiation dose (related to the reparable region).

According to this model, the survival fraction is:

Where S is the cell survival fraction, D the total dose, and α and β are the descriptive parameters of the model.

Constant α is the coefficient of proportionality of the total dose needed to achieve an effect, where the produced lesion cannot be reparable, called lethal damage. The parameter β represents the coefficient of proportionality of the square of the dose needed to achieve an effect where the lesion in reparable, also called sub-lethal damage. It is important to consider that the inductive particles of the reparable lesion can act separately for a period of time. After a critical period, the injury is repaired.

The Linear Quadratic model of cell survival quantifies using its two terms, the relative importance of each of the possible mechanisms of cell death, giving more importance to the dose per fraction, than to the dose escalation, taking into account the repair capacity of the injury, using coefficients α and β .

Figure 5 analyses the effect that the LET has on cell survival. For low LET radiations, such as photons, βD2 is insignificant at a low dose, and cell survival is proportional to the single dose. Thus, the survival curve is linear. At higher doses, cell survival is proportional to the square of the dose and the curve tends to be concave and downward. In high LET radiations, such as protons, alpha particles and neutrons, β is zero, which makes the survival curve linear [1].

When, in the Linear Quadratic model [13], the linear term equals the quadratic, meaning the proportion of reparable lesions equals the irreparable, the model shall be expressed as:

This means that the α/β coefficient (also called effectiveness coefficient) equals the dose where reparable and irreparable injuries are the same (see Figure 5). Additionally, parameter α /β is a measure of how fast the survival curve starts to decline in a significant way [10]

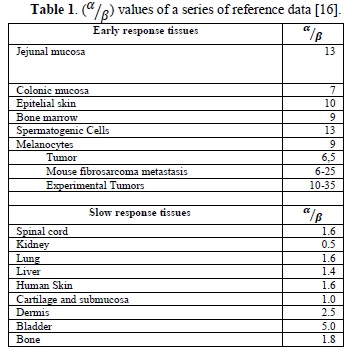
Parameter α/β is important for radiotherapy. Table 1 shows some of the characteristic values of α/β for some tissues. One interpretation of this coefficient states that a high α/β belongs to cells with a high turnover capacity and a low repair capacity. Hence, these characteristics show that the exhaustion in this type of cells produces acute clinical effects.

On the contrary, there is another group of organism cells whose effectiveness coefficient (α/β) is low. This belongs to cells which are more differentiated, have a slow turnover capacity and better tolerate irradiation through low fractions, due to a notable capacity to repair sub-lethal lesions. Therefore, it can be inferred that the chronic effects appear when there is an exhaustion of slow turnover cells, and hence their alterations are shown after a prolonged period of tolerance.

In order to apply the linear quadratic model to dose fractionation in time intervals, three conditions must be satisfied:

1. The dose must be administered in much shorter periods than the average time of sub-lethal repair.
2. This model does not take cell repopulation into account.
3. Two consecutive dose fractions must be administrated in a time interval that allows the complete repair of sub-lethal damage for healthy tissue.

Under these assumptions, the mathematical form of the linear quadratic model is established for a fractionated administration of the dose:

Where D is the overall dose administrated in N fractions, dk is the dose of the k^th fraction.

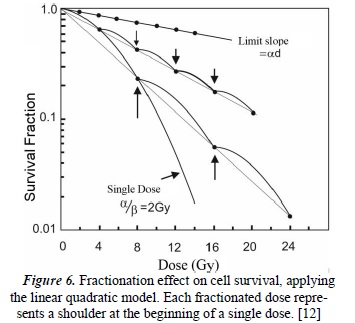
Figure 6 shows the behavior of the fractionated dose in equal time intervals. Conversely, when the size of the dose per fraction decreases, the total dose required to achieve a determined isoeffect increases more for slow response tissues than for acute response tissues. This technique is the basis of radiotherapeutic techniques, such as hyperfractionation, which seeks to control tumors (with responses similar to the acute response tissues) without damaging the adjacent differentiated tissues. It is necessary to clarify that between each small dose, a period of time that allows for sub-lethal repair is necessary [12].

4. Conclusions

This paper sets the conceptual bases for the study of Physico-Mathematical models, which have been used in the development of radiobiology. In addition, it is only the beginning of deeper studies on the current models, such as the quadratic model of cell survival curves. This model is still being researched, with the purpose of consolidating it as a solid theoretically-based model, using mechanistic ideas and statistical arguments.

In recent years, the linear quadratic model has been widely used in radiotherapy, using both single and fractionated doses. Its simplicity allows comfortable application in clinical contexts since, endowed with biological parameters with easy interpretations, it allows a satisfactory description of the cell survival curves in homogenous cell populations.

Along with the technical processes and technological developments, one of the main tools for improving clinical results in radiotherapy (with minimal conditions in healthy tissues) is the integral development of radiobiology. This provides the conceptual basis for cellular behavior under the effects of ionizing radiation and highlights new courses of action in the face of oncological disease.

Notes:

¹ Dose: the energy absorbed per unit mass, the unit is the joule per kilogram (J kg-1) and is given the special name gray (Gy).

References

[1] M. C. Joiner y A. Van der Kogel, «Introduction: The significance of radiology and radiotherapy for cancer treatment,» de Basic Clinical Radiobiology fourth Edition, London, CRC Press, 2009, p. 4.         [ Links ]

[2] M. Hillar, Radiation Safety Training Guide., Texas: Law of Bergonie & Tribondeau, 2006, p. 15.         [ Links ]

[3] G. B.S, «Physics and Radiobiology of Nuclear Medicine,» de Radiation Biology, New York, New York, Springer, 2004, pp. 226-255.         [ Links ]

[4] M. Strandqvist, «Studien über die kumulative wirkung der röntgenstrahlen bei trakionierung,» Acta Radio Supp (Stockh), vol. 55, pp. 1-300, 1944.         [ Links ]

[5] L. Cohen, «Theoretical "Iso-survival" formulae for fractionated radiation therapy,» The british Journal of radiology, vol. 41, nº 487, 1967.         [ Links ]

[6] F. Ellis, «Dose, time and fractionation: A clinical Hypothesis,» Clinical Radiology, vol. 20, nº 1, pp. 1-7, 1969.         [ Links ]

[7] J. F. Fowler, «The estimation of total dose for different numbers of fractions in radiotherapy,» The British Journal of radiology, vol. 38, nº 449, 1965.         [ Links ]

[8] J. Fowler y B. E. Stern, «Dose-time relationships in radiotherapy and the ability of survival curve models,» The Brtish Journal of Radiology, vol. 36, pp. 163-194, 1973.         [ Links ]

[9] C. Orton y F. Ellis, «A simplification in the use of the NSD concept in practical radiotherapy,» British Journal of radiology, vol. 40, pp. 529-537, 1973.         [ Links ]

[10] P. Rubin, Clinical Oncology, A multidisciplinary approach for physicians and students, New York: W.B. Saunders Company, 2001.         [ Links ]

[11] E. J. Hall, Radiobiology for the Radiologist. Ed. Second Edition., Harper & Row. Publishers Philadelphia, 1978.         [ Links ]

[12] C. Pérez y W. Brady, Principles and Practice of Radiation Oncology, Philadelphia.: Raven Publishers, 1997.         [ Links ]

[13] M. Gil Gayarre, Manual de radiología Clínica, Barcelona: Harcourt Brace, 1994.         [ Links ]

[14] S. Lehnert, Biomolecular Action of Ionizing Radiation, Methods of Cell and Molecular Radiobiology., Montreal: Taylor & Francis, 2008.         [ Links ]

[15] S. Lehnert, Biomolecular Action of Ionizing Radiation, Cell Death, Cell Survival, and Adaotation, Montreal: Taylor & Francis, 2008.         [ Links ]

[16] J. Ciudad, D. Guiraldo, A. Sanchez, W. Sanjuanbenito y S. Velazquez, Radiobiología Clínica, Principios Básico., Madrid: Sociedad Española de Física Medica, 2003.         [ Links ]