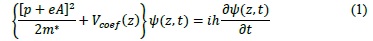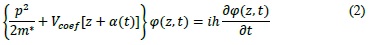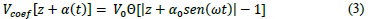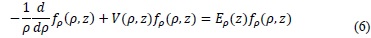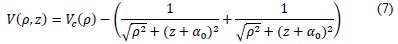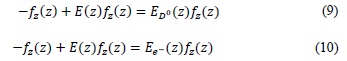Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Tecciencia
Print version ISSN 1909-3667
Tecciencia vol.9 no.17 Bogotá July/Dec. 2014
https://doi.org/10.18180/tecciencia.2014.17.10
DOI: http://dx.doi.org/10.18180/tecciencia.2014.17.10
Effects of a high intensity laser in the binding energy of a donor impurity D0
Efectos de un láser de alta intensidad en la energía de enlace de una impureza donante D0
Armando Castellanos Jerez1 Leonardo Vega Vargas2
1 Universidad Industrial de Santander UIS, Santander, Colombia, wlvegav@gmail.com
2 Universidad Nacional de Colombia, Bogotá, Colombia.
How to cite: Castellanos, A.C.; Vega Vargas, W., Effects of a high intensity laser in the blinding energy of a donor impurity, TECCIENCIA, Vol. 9 No. 17, 78-83, 2014, DOI: http://dx.doi.org/10.18180/tecciencia.2014.17.10
Received: 08/08/2014 Accepted: 12/09/2014 Published 30/12/2014
Abstract
In this paper, we present theoretical results on the effects of an intense laser on the binding energy in the ground state of a neutral donor impurity D° located in a gaas-(Ga,Al)As quantum well, embedded in a quantum wire. We calculated the behavior of the binding energy, considering different parameters such as the radius of the wire, the intensity of the laser beam, different concentrations of aluminum in the heterostructure, and the position of the impurity within the quantum well. By varying the latter parameter, we observed a new behavior of this energy in the presence of an intense laser.
Resumen
En este trabajo presentamos los resultados teóricos de los efectos de un láser intenso en la energía de enlace en el estado base de una impureza donadora neutra𝐷0 Ubicada en un pozo cuántico de gaas(Ga,Al)As embebido a su vez en un hilo cuántico. Calculamos el comportamiento de la energía de enlace teniendo en cuenta diferentes parámetros como el radio del hilo, la intensidad del haz laser, las diferentes concentraciones de aluminio en la heteroestructura y de la posición de la impureza dentro del pozo cuántico; al variar este último parámetro pudimos observar un nuevo comportamiento de esta energía en presencia de un láser intenso.
1. Introduction
In recent decades, low-dimensional structures such as quantum wells (qws), quantum wires (qwws), quantum dots (qds), and other configurations have been studied with special interest [1]. The changes that these structures undergo when they experience external perturbations such as electric and magnetic fields, lasers, and pressures, have been studied in order to manipulate their various electronic states and create novel, diverse optical and electronic devices at a nanoscale. In addition to this, there has been particular interest in heterostructures designed to combine elements from groups III and IV of the periodic table [2]. Some of the best known include: gaas, INPB, and gasbyinas. Of these, we chose the first (gaas). The decision was based on its theoretical and experimental development and its many expected applications due to its optoelectronic properties, which can improve the development of much faster computers, higher sensitivity detectors, more efficient solar cells, etc. [3] [4].
There have been previous studies on impurities in quantum wells and wires under the influence of intense lasers, but none on the configuration of a quantum well within a quantum wire [5] [6]. Hence, greater additional confinement gives us different results than those obtained by configurations of impurities within wells or quantum wires separately. This can lead to experimental development since we can create a larger confinement and in so doing manipulate the movement of the electron in a single direction with great energy efficiency. For this particular approach, we used effective mass approximation and adiabatic approximation.
In this paper we studied the effects of an intense laser on the binding energy in the ground state of a neutral donor impurity, placed in different positions on the quantum well. We also considered the efecto de vestimiento of the laser on the Coulomb impurity and potential geometrical confinement. Both potentials were shown to play a key role in the binding energy of the impurity. We examined the behavior of the binding energy by varying parameters, such as the intensity of the laser beam and the radius of the quantum wire, among others.
2. Quantum confinement
Analyzing the dimensional structures compared to the Broglie wavelength in at least one dimension, quantum effects can be observed in semiconductors with a thickness of 10 to 100 times the lattice constant of these materials [7].
Quantum confinement systems can be constructed by combining two direct energy bandgap semiconductors. Depending on the degree of confinement that the carriers experience, we can experimentally obtain various types of structures thanks to the accelerated development of growth techniques in different types of semiconductors.
Many of the quantum confinement devices have been developed by the successive deposition of alternate layers of two different semiconductors. Examples of these techniques are the molecular beam epitaxy method (MBE) or metal-organic chemical vapor depositions [2]. Although there are other techniques to create such devices, they differ in the creation process. One example is the e-beam lithography technique, which has an advantage in that it can model different types of structures to different tastes. However, using these techniques and the combination of them and others has enabled the development of more complex structures of high quality, while minimizing manufacturing defects and unwanted tensions.
To perform the calculations, we chose the heterostructure made by the union of gaas and (gaas)Al. This was because in the experimental phase, the lattice parameter mismatch between epitaxial layer and substrate is 0.1% when we use the MBE technique, whereas using other systems such as (gaas)In, the same value reaches 7.2%, and the smaller this mismatch is, the better prepared the heterostructure will be. Using the chosen heterostructure to elaborate our calculations, a potential well is created in its two joints whose barrier height depends entirely on the concentration of aluminum. This can be calculated according to the following relationship V_E = 0.65 * (1.125 x + 0,37x ^ 2), where the value of x represents the proportion of aluminum.
3. Potential coating geometric confinement
When a quantum well is in the presence of a monochromatic laser beam - linearly polarized in the axial direction (z axis) - we can study the electronic states of the confinement potential and the electromagnetic field, including the term representing the external field in the kinetic part of the Hamiltonian operator. This semiclassical operation is a combination of the quantum description of a particle motion and the classical description of the radiation field. Thus, it gives us a semiclassical time-dependent equation.
Where m* is the effective mass of the electron in the structure.
For fields that do not vary significantly in a large region of space, we can apply the dipole approximation  (z, t) ≈
(z, t) ≈ 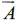 (t), as long as the wavelength of the laser beam we use is much bigger than the width of the quantum well. In the Coulomb gauge, the electromagnetic fields are related to the vector potential through
(t), as long as the wavelength of the laser beam we use is much bigger than the width of the quantum well. In the Coulomb gauge, the electromagnetic fields are related to the vector potential through 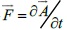 . For any oscillation
. For any oscillation 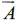 (t), the Kramers-Hennebergerde unitary transformation can be translated into equation (1) to transfer the kinetic time dependence to the potential term in the Hamiltonian operator on the left side of the equation. Aferwards, that transformation becomes:
(t), the Kramers-Hennebergerde unitary transformation can be translated into equation (1) to transfer the kinetic time dependence to the potential term in the Hamiltonian operator on the left side of the equation. Aferwards, that transformation becomes:
The motion of the electron, in the presence of an external electromagnetic field, can be described by an accelerated approach that oscillates in phase with the electromagnetic field. Considering Kramer's approach where the electrons interact with the oscillatory potential, we obtain:
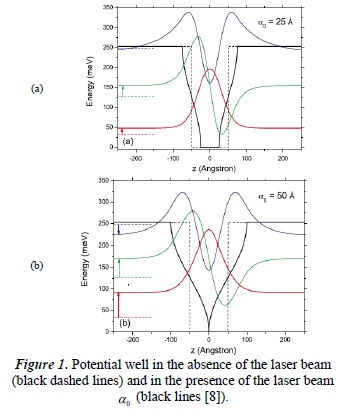
The geometric confinement potential is modified by the parameter α(t) which contains α0 = 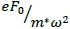 because of the laser beam interaction. Additionally V0 is determined by the concentration of aluminum in the heterostructure and gives the barrier height in the rectangular well. The step function determines the shape of the quantum well in the presence or absence of the laser beam. An expansion of the Floquet-Fourier series was applied in the above equation to expand it as periodic potential, and thus give us the ability to model it on a computer [8]
because of the laser beam interaction. Additionally V0 is determined by the concentration of aluminum in the heterostructure and gives the barrier height in the rectangular well. The step function determines the shape of the quantum well in the presence or absence of the laser beam. An expansion of the Floquet-Fourier series was applied in the above equation to expand it as periodic potential, and thus give us the ability to model it on a computer [8]
In the above graphics we can see how the potential wells are deformed as the value of increases and it reaches a point where we can observe the large confinement effect in an axial direction.
4. Model
Consider first that use a donor impurity D° (ie: a germanium atom) that breaks the translational symmetry of the crystalline structure in its location, with the appearance of additional potential due to the type of impurity. Depending on the dimensions of the geometrical confinement experienced by the impurity and its position, it will have different values in its binding energy.
Due to the effects caused by the impurity within the crystal lattice, the analysis of the electron in the crystal has led to some complications. Besides the crystal potential, the electron feels an asymmetrical attraction potential, rendering impossible an exact solution of the Schrödinger equation for this system. To remove one of the problems, we have applied electron effective mass approximation, taking advantage of the fact that the band structure of the semiconductor is almost parabolic in the bottom of the band, and its effective mass is approximately isotropic. The value of the mass varies according to the relation m*e = (0,067+0,083x)m0 where m0 is the electron mass in vacuum.
Overall, we obtain the Schrödinger equation in cylindrical coordinates:
However, it is important to highlight that the presence of the laser beam on the donor impurity can be analyzed as a three-particle system: one positive ion and two electrons. This does not have an exact solution, and even numerically it has various complications. For this reason, we used the adiabatic approximation to separate the Schrödinger equation into two equations, one depending on its "fast" motion (radial) and the other depending on its "slow" motion (axial). It was therefore proposed that the radius of the wire was much smaller than its length, thus having greater radial confinement and, consequently, a more significant contribution to the binding energy. For this system, it is possible to divide the wave function into its radial and axial components, as follows:
This is a numerical function and it is very useful for solvingour systems equation. First, it is only used in one direction, in order to calculate the energy contained in the nucleus and the electron separately. To be able to do this, the motion in the direction of the z-axis is "frozen" and the following equation in a radial direction is obtained:
Where the potential V is due to the Coulomb interaction and the geometry of the wire, which is altered because of the presence of the laser beam:
And Vc(ρ) is defined as:
Equation (6) is solved via a trigonometric scan, and thus the values of Eρ(z) are calculated along the width of the well.
Afterwards, the motion in the z-axis is "unfrozen" and the motion in the ρ axis is "frozen", in order to calculate the energy of each particle in its two components. We solve the Schrödinger equation through a new trigonometric scan for the nucleus of the impurity and its electron:
Where E(z)=Eρ(z)+Vconf(ρ,z)
Now, by simply subtracting the energy values previously calculated in (9) and (10), the operation Eb(z)=Ee_(z)-ED°(z) is performed, in order to obtain the value of the binding energy for each position in the well in the z coordinate.
5. Results
The results obtained in this paper were calculated taking into account the values of the effective "Bohr radius"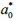 = 9,87nm and the Effective Rydberg constant
= 9,87nm and the Effective Rydberg constant 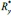 = 5.72meV. The energy values in the graphics are given in
= 5.72meV. The energy values in the graphics are given in 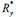 and in nm for the position and the value of parameter
and in nm for the position and the value of parameter 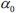
- - Binding energy of an impurity Dº in function of parameter
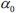 .
. The first result we obtained was the binding energy of an impurity Dº in function of a parameter 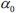 , for an aluminum concentration given by x=0.3 and, thus, a quantum well barrier height of 39.83Ry*.
, for an aluminum concentration given by x=0.3 and, thus, a quantum well barrier height of 39.83Ry*.
In these graphs, we can observe the behavior of the binding energy and the fact that as the value of 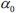 increases, the value of the binding energy decreases. This happens due to the high intensity of the laser beam; it adds some energy to the electron to make it move away from the nucleus of the impurity. In Figure 2b, we can observe a better contribution to the calculation of the adiabatic approximation, because the width of the well is larger than the radius of the wire. For this reason, the two waves that are observed in the graph are more noticeable. The first wave is due to the effect of the geometric confinement felt by the impurity, and which is now larger than the separation effect of the laser beam. The second wave is due to the effects which are produced when the quantum well is deformed and the electron oscillation is greater.
increases, the value of the binding energy decreases. This happens due to the high intensity of the laser beam; it adds some energy to the electron to make it move away from the nucleus of the impurity. In Figure 2b, we can observe a better contribution to the calculation of the adiabatic approximation, because the width of the well is larger than the radius of the wire. For this reason, the two waves that are observed in the graph are more noticeable. The first wave is due to the effect of the geometric confinement felt by the impurity, and which is now larger than the separation effect of the laser beam. The second wave is due to the effects which are produced when the quantum well is deformed and the electron oscillation is greater.
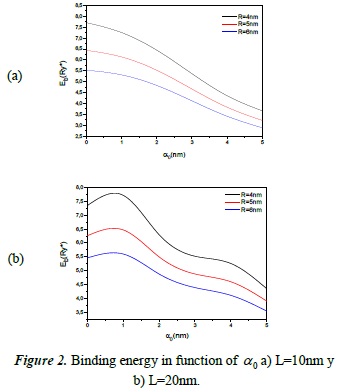
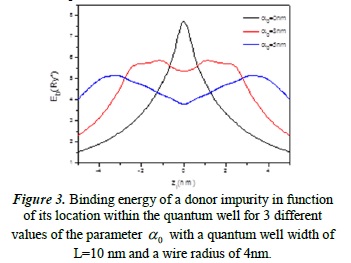
Binding energy of an impurity Dº in function of its location within the quantum well.
In Figure 2 we can observe the binding energy of the impurity D° in function of its location within the quantum well (axially), but radially centered. Additionally, it is shown for different values of 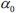 .
.
The black line represents the behavior of the binding energy for different locations within the quantum well in the absence of the laser beam. This result is consistent with those previously reported for similar geometrical configurations with particles in the presence of intense lasers. In the other two lines the behavior of the binding energy is shown, when the impurity is subjected to the laser beam.
In its centered location we can observe a minimum, which occurs because in this location the impurity feels less confinement effect on one or both sides of the quantum well, and a higher separation effect due to the laser. It is possible that the other waves, with the two maxima, are produced by a mix of the laser beam and the geometrical confinement effects.
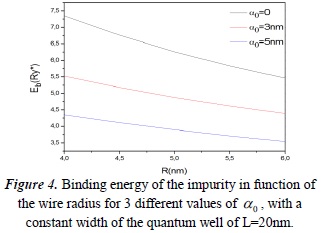
- - Binding energy of an impurity Dº in function of the wire radius.
In the above graph, we see that when the radial confinement is bigger, the binding energy of the impurity is higher, as expected, and in the absence of the laser beam, this energy is greater than with it. This is due to the lack of extra energy in the electron for it move away from the nucleus of the impurity and overcome the Coulomb potential. Something different occurs when it is in the presence of the laser beam, as seen in the red and blue lines - the greater the intensity (the greater 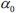 is), the lower the binding energy, thus reaffirming the predictions.
is), the lower the binding energy, thus reaffirming the predictions.
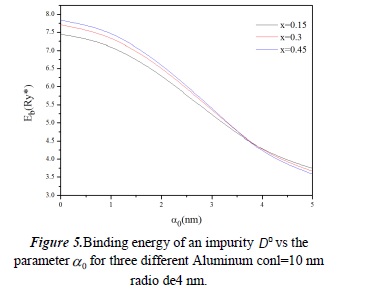
Binding energy of an impurity Dº in function of the parameter 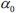 for different aluminium concentrations.
for different aluminium concentrations.
It can be observed that the larger the confinement produced by the height of the potential barrier, the higher the binding energy. This behavior continues until the parameter 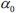 reaches a value of 3.7nm, where the behavior is reversed. This happens because more energy is needed to deform the potential well with higher barriers than when they are smaller.
reaches a value of 3.7nm, where the behavior is reversed. This happens because more energy is needed to deform the potential well with higher barriers than when they are smaller.
6. Conclusions
We have presented a theoretical approach of the effects of an intense laser beam on a neutral donor impurity located in a quantum well, which is also within quantum wire with semiconductor materials of low dimensionality. We analyzed the interaction between light and mass, which takes into account the confinement potential vestimiento. All of the results obtained in this study are consistent with the behavior of the binding energies in previous research by other authors with similar configurations of confinement.
The graphs show that as confinement increases, either radially or by reducing the size the quantum well, the binding energy of the impurity increases. This occurs in the presence or absence of the laser beam, because the geometric confinement heterostructure affects the proximity of the electron and the nucleus of the impurity. This property can have important consequences in optical applications involving semiconductor structures of low dimensionality.
Another important effect of the laser beam on donor impurity is to separate the electron from the nucleus of the impurity, causing the binding energy to decrease. For this reason, we observed that as the intensity of the laser beam increased, the binding energy noticeably decreased.
Our research is novel because there is not, to date, a study of the behavior of binding energy when the impurity is doubly confined and at the same time in the presence of a laser beam using the presented type of heterostructure. By being able to modify and increase the value of the binding energy in a controlled manner, we can expect that some current electrical storage and optoelectronic devices can be modified to function in a much more efficient way.
The property of decreasing the binding energy by using a laser beam should open the door to further studies on the optical properties of quantum well wires for high-level practical applications. This effect is useful and leads to the creation of sensors with higher precision and control. As we observed, many parameters can be modified to obtain the appropriate energy values for each particular case.
References
[1] E. Tangarife, M. de Dios-Leyva y C. Duque, «Efecto combinado de presión Hidrostática y campos eléctrico y magnético sobre la recombinación electrón- Hueco en pozos cuánticos de GaAs(Ga, AI)As,» Revista Colombiana de Física, vol. 38, nº 2, pp. 517-520, 2006. [ Links ]
[2] P. Aristizabal, R. Restrepo, W. Ospina y C. A. Duque, «Energía de enlace de excitones en pozos cuánticos de GaAs/Ga1-xAlxAs,» Revista EIA, nº 7, pp. 121-126, 2007. [ Links ]
[3]: D. Perea, W. Sánchez y N. Porras- Montenegro, «Cálculo de los Primeros Estados Energéticos en Sistemas de Pozos Cuánticos Acoplados de GaAs-(Ga,As)Al, Para Varios Anchos de Pozo y Diferentes Concentraciones de Al,» Revista de la Sociedad Colombiana de Física, vol. 41, nº 1, pp. 11-13, 2009. [ Links ]
[4] J. H. Marin, F. Garcia y F. J. Betancur, «Electron hole pair in a quantum pyramid,» Revista Colombiana de Física, vol. 37, nº 1, 2005. [ Links ]
[5] Z.-. Y. Deng, T.-. R. Lai y J.-. K. Guo, «Effects of dielectric mismatch on the impurity binding energies in GaAs-Ga1-xAlxAs quantum wells,» Journal of Physics: Condensed Matter, vol. 50, nº 8, pp. 5732-5735, 1994. [ Links ]
[6] M. Santhi y J. Peter, «Intense field effects on shallow donor impurities in a quantum wire,» The European Physical Journal B, vol. 71, nº 2, pp. 225-231, 2009. [ Links ]
[7] D. Fuster Signes, ICMUV, CNM, Valencia, 2003. [ Links ]
[8] F. M. Lima, M. Amato, A. Nunes, L. Fonseca, B. Ender y E. da Silva, «Unexpected transition from single to double quantum well potential induced by intense laser fields in a semiconductor quantum well,» Journal of Applied Physics, vol. 105, nº 12, 2009. [ Links ]