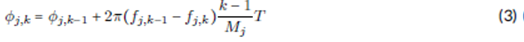1 INTRODUCTION
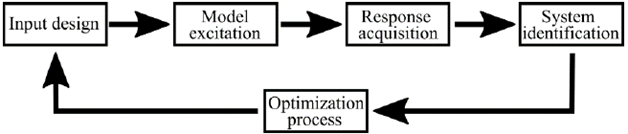
System identification (Sys-ID) is a method for developing mathematical model that describes system dynamics, based on observation or measurements of input and output for the system under study. To identify and quantify aircraft response, control surface excitations must be performed to take the aircraft out of it equilibrium state. Process schematic is shown in Fig. 1. Sys-ID allows to find more accurate results related to aerodynamic derivatives when compared with methods like Computational Fluid Dynamics (CFD) simulations or wind tunnel test. Sys-ID process uses the real scale aircraft characteristics. The development of high accurate aircraft simulation models based on data obtained from identification techniques is an important research topic. Its applications are the development of flight simulation models and the design of control laws including stability augmentation commands, performing adaptive control and reconfiguration based on external disturbances and environmental condition. To perform the system identification a specific control signal is applied to the aircraft model and its response is recorded [1,2,3,4,5].
To detect the specific physical characteristics of the aircraft special flight maneuvers are performed. These maneuvers are divided into longitudinal and lateral motion and performed separately to acquire the required information. Nowadays engineers consider new optimized ways to get model information to reduce flight test campaign time and costs. To achieve this, it is possible to design maneuvers in which flight control surfaces are deflected simultaneously. Control commands are generated by simultaneous excitation of the control surfaces. Relative Peak Factor RPF minimization is preferred because it reduces the control surface deflections by minimizing the energy input. Multisine excitations can be used to achieve this purpose. This method is based on small perturbations to keep the aircraft as close as possible to the equilibrium state while keeping the accuracy of the estimate model. In order to ind signals with these characteristics, Schroeder developed a model that proves that a phase-shifted sum of sinusoids can be used as input signals with low peak factor and good frequency content [6]. A specific power spectrum must be obtained to accomplish this aim. This task can be carried by using engineering based approach based on experience or more efficiently by using Lichota Method for maximizing the information stored from the aircraft response. Lichota method is a bio-inspired method based in Genetic Algorithm (GA) optimization technique to obtain adequate input energy content for a specific aircraft model [7,8, 9,10,11,12].
In this paper the aircraft under study is assumed to be a rigid body. Forces and moments acting on it arise from aerodynamics and propulsion characteristics. Mass and geometry symmetry is assumed along the longitudinal plane. By implementing 4-M methodology the model derivatives can be estimated. This method has some advantages like reduced consumption of money and time. It also deals with complex maneuvers in flight, which cannot be replicated in CFD and wind tunnels tests [1].
2 MATERIALS AND METHODS
In the study two set of deflection sequences were created based on multisine control signals. Various cases were considered basing on if a-priori knowledge based on system dynamics was included. For the first case no a-priori information was added during the computations to calculate the multisine control signals using a Matlab based script [13]. For the second case, a-priori information in terms of stability and control derivatives was used to compute the signals.
Simultaneous control vectors with minimum input amplitudes, wide-band frequency content and orthogonality in both the time domain and the frequency domain were generated. The signals are phase-optimized multisine sweep. Each set of data has minimized RPF for a designated power spectrum in the selected frequency range. Only ailerons and rudder were analyzed to obtain coupled lateral and directional derivatives information. The uniform power spectrum was used in the first case. In the second case the non-uniform power spectrum was obtained through numerical optimization (GA) [11,14, 15].
An aircraft model was excited by the control vectors. For each case the angle of attack, sideslip angle, linear velocity, roll, pitch and yaw rates, bank and pitch angles and linear acceleration magnitudes were registered to perform the Sys-ID process. This project pretends to determine if including a-priori knowledge in the system inputs design will allow us to obtain estimates with higher accuracy. After performing the maneuvers, resulting data was used to identify selected aircraft aerodynamic coefficients through Output Error Method and Maximum Likelihood Principle [10,11] [13] [16].
2.1 First case: Uniform Power Spectrum
For this case, the dynamic information of the aircraft was not included to calculate the orthogonal multisine control vector. A uniform distributed power spectrum was used along the airplane selected frequency range as set in Table 1. The orthogonal harmonically related multisine inputs with minimized peak factor was obtained. The control vector u consists of the sum of harmonic sinewaves which have individual amplitude A k and phase shift angles 4>k as shown in Eq. (1) [17]:
where ∫ k from k = 1 to M are consecutive harmonic frequencies and t is the time. A vector ∫ u was set as an input for the excitations. The signal was divided according to the harmonic frequencies that were assigned to ailerons and rudder. To obtain mutually orthogonal inputs, it was required to assign different harmonics to each flight control. For ailerons ∫0,3∫0,5∫0,... were assigned and for the rudder 2∫0, 4∫0,6∫0... were used. This distribution gives orthogonality in frequency domain as distinct spectral lines compose the frequency content of each input. Due to the orthogonality properties of the sine function, the signal time domain orthogonality is achieved [2]. The range of frequencies was stablished from 0 to 2 Hz typical for a large-scale aircraft. Control surfaces excitation lasted for 20 seconds, however the total maneuver time was 40 seconds. A total of 40 harmonics were analyzed.
The magnitude of the power spectrum was constant along the frequency range. The phase shift angles 4> k for each control surface were chosen to increase the efficiency of the input signal. From equation 2 was obtained a low RPF with a maximum energy and minimum amplitude range input [2] [13].
where j = 1 corresponds to ailerons and j = 2 to rudder. The initial values for the phase shift angles were calculated by using the equation 3 developed by Schroeder [6]:
The generated vector must start and finish with zero value to keep and return the aircraft at equilibrium position before and after the maneuver. For this reason, the signals were shifted on time. For all the signals excitation started at 10 seconds and lasted for 20 seconds.
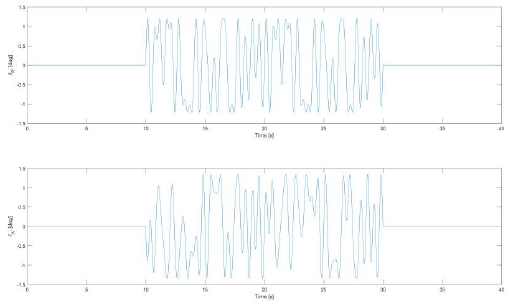
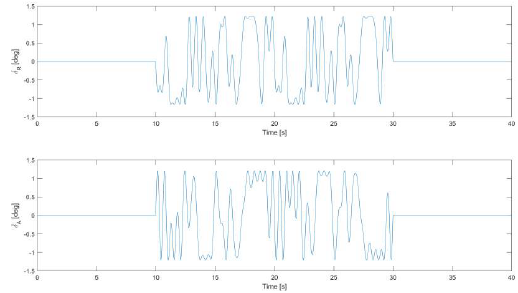
After calculations the control inputs and RPF for each excitation were obtained. Fig. 2 presents the control vector for ailerons and rudder as a function of time.
2.2 Second case: Non-uniform Optimized Power Spectrum with Genetic Algorithm.
In this case, the RPF was optimized using a bio-inspired optimization method, such as GA. The procedure belongs to evolutionary algorithm class and is inspired by natural selection based on crossover, mutation and selection that mimics biological evolution process. The GA at each step selects individuals from a specific population based on decision variables to produce the children for the next generation. By repeating the process on each generation, the individuals evolve towards an optimal solution.
Marchand method was implemented based on the a-priori known stability and control derivatives [18]. Bode plots for lateral and directional derivatives were obtained from literature available information [19]. They were computed for the rolling moment L, the yawing moment N and the lateral force Y for both ailerons and rudder. With the Bode plots it is possible to determine the frequency ranges which are more appropriate to obtain accurate information from the performed maneuvers. A ponderation was developed in the frequency domain to calculate weighting factors. The magnitude of the weighting factors was stablished like a threshold in the order of one decade below in the logarithm scale. The maximum range in the plot was determined along the range of the frequencies under study (0 to 2 Hz) from the graphs and corresponding magnitudes of each plotted magnitude. From the calculated differences a ponderation was computed. The lower the difference from the threshold, the higher the assigned ponderation. For each control surface the obtained ponderation distribution was assigned to 20 harmonic frequencies that compose the power spectrum.
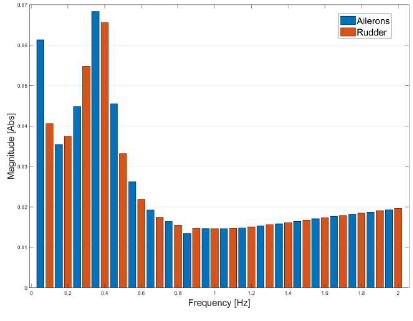
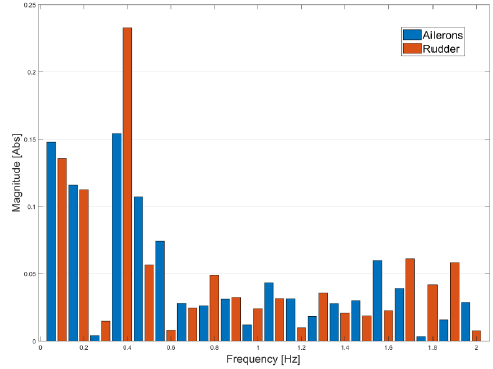
Contributions were added for each control surface and then normalized in a way where the sum of all the power spectrum components is equal to one. Fig. 3 presents the reference power spectrum for both the ailerons and rudder. From the plot it can be seen that in this study for the identification process the information obtained at high frequencies provides less content then at low frequencies the information is more accurate for the study of both control surfaces.
The optimization algorithm begins by creating a random initial population. Then a sequence of new population is created. At each phase, the current individuals are used to create the next generation. To do so the algorithm classifies the individuals according to a fitness parameter, the RPF. The method selects a group of individuals in the current population called parents who contribute their genes coded as numbers in a vector to produce new children. The parents are selected based on their fitness. The children are produced by crossing or mutating the vector entries of parents. The current population is replaced by the next generation and the process is repeated until a determined stopping criterion is achieved.
For the current project, 50 individuals were randomly created as the initial population. Each of them was represented by a power spectrum distribution. Twenty features determine their individual characteristics and each one corresponds to an individual harmonic in the power spectrum matrix. Features were coded with binary numbers (genes). Chromosomes were converted into decimal scale and multiplied by weighting factors contained in the reference power spectrum to include the a-priori knowledge.
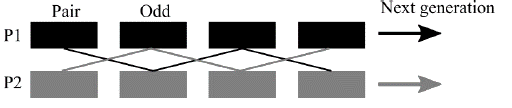
After the individuals were created the selection principle was applied to the calculated population. Roulette Wheel Selection (RWS) method was used for this task, otherwise a super individual would dominate the population. RWS works based on the evaluation of a fitness function. Probability of parenthood is proportional to individual fitness. For this specific case, low RPF magnitude were desired among the analyzed population. Individuals with a low RPF had more chances to be selected for recombination and produce the next generation. RWS method was applied to select well suited individual and produce pairs. RPF was obtained from the evaluations carried for each excitation, which means that 50 solutions were computed. Afterward, RWS process was performed to obtain parents that will produced the best individuals for the next generation. The algorithm creates crossover children by mixing pair of parents by crossover as shown in Fig. 4. Odd and pair genes are combined from two individuals to create two new children.
The newly obtained population replaced the previous one and process was repeated 50 times. To introduce more diversity and uncertainty in the population, a mutation operator was added during the process which changed some elements on the DNA during the combination. This was performed by creating a random vector containing decimal numbers from zero to one. A threshold of 0.95 was set for the mutation. If a number is bigger that the stablish threshold a mutation was imposed to the corresponding gene position in the newly created child. After the last generation, the individual with the lowest RPF was selected to produce the orthogonal multisine control vector u.
The results of the optimized power spectrum distribution obtained after 50 generations for both the ailerons and rudder are presented in Fig. 5.
The orthogonal multisine control input signals obtained from the optimized power spectrum are shown in Fig. 7.
2.3 Model excitation
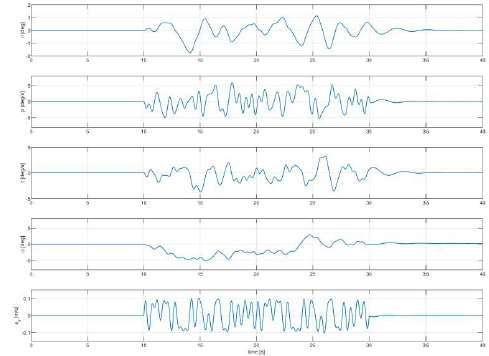
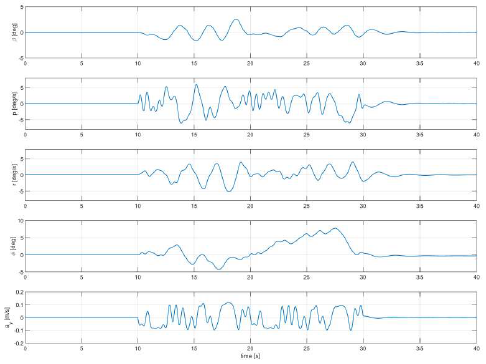
After using the control signals to excite the aircraft model its response in time domain was obtained. The formulation allowed to obtain information regarding the sideslip angle (ϐ), the roll rate (p), the yaw rate (r), the roll angle (<J>), and lateral acceleration (ay). Fig. 6 presents the time response of the model after application of the first set of control signals. Fig. 8 shows the model response to the second set of input signals. The maneuver lasted for 40 seconds in both cases.
3 RESULTS AND DISCUSSION
System identification is used to stablish for estimating the aerodynamic derivatives of an aircraft. Many different methods have been used among the history as reported by Carnduff [20]. Maximum likelihood principle and Output Error Method were used by NASA [21] to identify stability and control derivatives of a Normal category Cessna U-206. Furthermore, time and frequency domain and output error method were applied by Morelli and Klein in the identification process of a Twin Otter airplane [22]. Moreover, a research conducted by Kim and Seong used the maximum likelihood method to identify the parameters of a general aviation canard aircraft [23]. For the present study, Maximum Likelihood Principle and Output Error Method were used to identify the Navion aircraft parameters.
An ordinary differential equations model involving the aircraft dynamic parameters, the input signals and the system response was used to identify the aerodynamic derivatives through OEM in the longitudinal and lateral directions. For the calculations the aircraft was considered as a rigid body where the inertial forces were not affected by the control surfaces deflections. Furthermore, the airplane is assumed to fly at constant speed during cruise flight segment, with all engines running at constant regimen providing constant thrust force magnitude. Due to short maneuver time, no significant fuel consumption was considered. The airplane has a symmetry condition along its longitudinal plane in terms of mass and geometry. Finally, turbulent effects were omited and good weather conditions were assumed.
After the system identification procedure was performed, the obtained data was compared with experimental data acquired from flight tests. Relative error e for each aerodynamic coefficient was calculated from the equation:
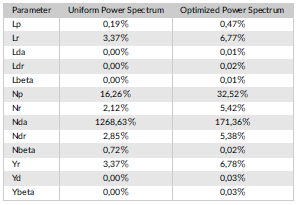
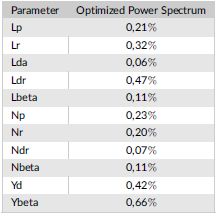
where Oi are aerodynamic derivatives and hat symbol denotes estimates. Results for the analyzed cases are presented in terms of relative error in the Table 2. For this case Nda, Yr were not estimated. 5 out of 11 estimates reduced the relative error magnitude when compared to the error obtained from the optimized power spectrum identification results. Further studies must be carried out to improve obtained results.
4 CONCLUSIONS
During this study, two maneuvers were performed an analyzed to estimate lateral-directional control derivatives. To achieve this goal, ailerons and rudder were deflected simultaneously. First test was based on orthogonal multisine inputs obtained for a uniform power spectrum. Second case was performed for a non-uniform optimized power spectrum with a bio-inspired procedure based on Genetic Algorithm optimization technique to obtain the input signals.
For the second case, a genetic algorithm was applied, natural selection-based process method which has the objective of improve the accuracy of the estimate values. The a-priori knowledge was introduced by multiplying weighting factors by the energy distribution obtained from Marchand method. A mutation operator was used to introduce more diversity to the solution.
The implemented methodology permitted to obtain a low relative peak factor signal. Used of the a-priori information led to obtain better power spectrum distributions.
This kind of investigations can involve different fixed-wing aircraft models because that are totally described in terms of aerodynamic derivatives. For this reason, the methodology of this study could be validated with other aircraft