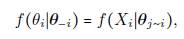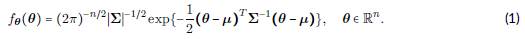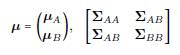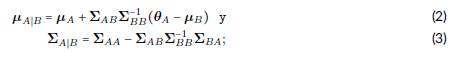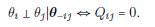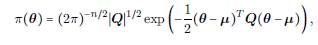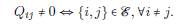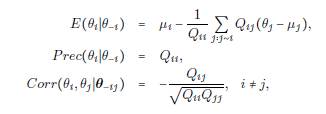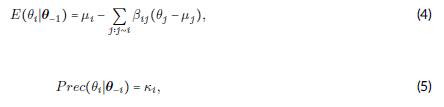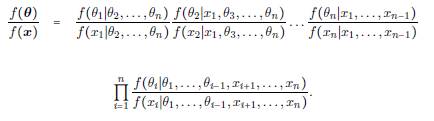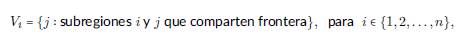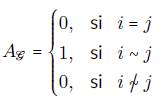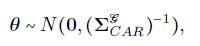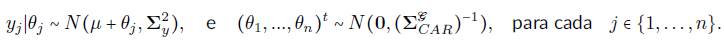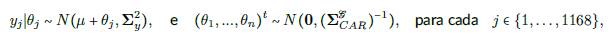1 INTRODUCCIÓN

Los modelos estadísticos para analizar datos espaciales se dividen en dos clases generales: modelos geoestadísticos con soporte espacial continuo y modelos en una lattice, también llamados datos de área, donde los datos se producen en una cuadrícula (posiblemente irregular), con un conjunto enumerable de vértices o ubicaciones. Estos modelos autoregresivos se utilizan en muchos campos, incluyendo la cartografía de las tasas de infecciones [¹], agricultura [²], econometria [³], ecología [⁴] y el análisis de imágenes [⁵]. En este trabajo, se presenta el modelo CAR como un ejemplo de los campos aleatorios gaussianos de Markov. El modelo CAR es un ejemplo dos campos aleatorios de Gaussian Markov [⁶]. Varios autores han analizado este modelo, mostrando las características de las covarianzas y las correlaciones dada una estructura espacial, por ejemplo, el modelo CAR produce variaciones no constantes en cada sitio, así como covarianzas desiguales entre regiones separadas por el mismo número de vecinos (ver [⁵], [⁷]), [⁸] estudió ampliamente la estructura de covarianza a priori que conlleva el modelo CAR. Encontró que la relación entre vecinos no parece tener explicación, ya que nodos con el mismo numero de vecinos y en vecindades similares tienen covarianzas diferentes. Luego, [⁷] en su artículo esclarece todos estas rarezas y concluye que el modelo CAR es afectado por sus vecinos de mayor orden.

El modelo CAR visualiza el dominio geográfico como un grafo no dirigido con un vértice en cada región y una arista entre dos vértices si las regiones correspondientes comparten un borde geográfico. Esto crea vecinos bien definidos para cada región, que se utilizan para definir la distribución conjunta o condicional. La distribución será la distribución multivariante normal.

El sistema de vecindad es un punto clave en los modelos autorregresivos (CAR) que se usan comúnmente en estadísticas espaciales. Para este caso, los grafos que apoyan la construcción del GMRF serán aquellos que expresen estas estructuras de vecindad. En este contexto, las aristas E en el grafo B = (G, E), representan las conexiones en la estructura geográfica y, en consecuencia, definen los vecinos que se utiliza para modelar la dependencia espacial.

Los componentes del vector θ son nodos del grafo. Supongamos que θ₁ ,..., θ _n sean las observaciones realizadas en las áreas 1,...,n. Denotemos por j ~ i que el nodo j es vecino del nodo i. El término condicional, en el modelo CAR se usa porque cada elemento del proceso aleatorio se especifica condicionalmente en los valores de los nodos vecinos. En este artículo se presenta cuales comando pueden ser utiles para construir mapas, grafos y las matrices de adyacencia necesarias para este tipo de análisis, a manera de ejemplo se presenta el mapa de Colombia y el uso de este modelo en R aplicado al caso de robos de celulares en Bogotá.

2 CAMPOS DE MARKOV GAUSSIANOS

Los campos aleatorios son distribuciones multivariadas que, en general, se usan para describir la asociación espacial entre las variables θ. 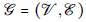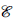Un campo aleatorio de Markov extiende el concepto de cadena de Markov a un contexto espacial y supone que dicha distribución conjunta de θ esta definida como sigue: sea un grafo con n vértices V donde cada uno representa una de las componentes del vector θ = (θ ₁ , θ ₂ ,..., θ _n ) y el conjunto de aristas que conecta dos vértices θ _i e θ _j ,. Asi,

con θ _j ∼ _i el vector formado por todos los componentes de θ quienes son vecinos de i. En esta sección discutiremos brevemente los campos aleatorios gaussianos de Markov que a menudo se usan como una distribución a priori para efectos espaciales.

Un campo de Markov gaussiano aleatorio (GMRF por sus siglas en inglés) es un campo de Markov donde la distribución del vector aleatorio (de dimensión finita) y una distribución normal o gaussiana satisfacen los supuestos de independencia condicional. Se puede encontrar una discusión detallada de GMRF en ([⁶]) y ([⁷]).

Todos los resultados válidos para la distribución normal también serán válidos para un GMRF. Por lo tanto, en la siguiente sección presentamos los resultados más relevantes de la distribución normal multivariante. Después de definir formalmente un GMRF con todas las propiedades heredadas de la distribución normal, presentaremos la conexión entre el grafo 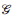y los parámetros de la distribución normal multivariada μ y Σ. Se mostrará que toda la información en el grafo se condensa en la matriz de covarianza Σ por medio de la matriz de precisión Q = Σ^-1, además, el vector promedio /lx no influirá en la estructura del vecindario del grafo.

3 LA DISTRIBUCIÓN NORMAL MULTIVARIANTE.

Para facilitar la comprensión de los campos aleatorios gaussianos de Markov, revisamos la distribución normal multivariante y algunas de sus propiedades básicas.

Un vector aleatorio n-dimensional θ _nx1 = (θ ₁ , θ ₂ ,..., θ _n ) ^T , n < ∞ tiene una distribución n-variada con vector de medias μ_nx1 y matriz de covarianza Σ_nxn si su función de densidad de probabilidad (pdf) toma la siguiente forma:

Esta distribución será denotada por θ~ N(μ, Σ) donde μ y Σ son tales que μ_i = E(θ _i ), Σ _i , = Cov(θ _i , θj), Σ_ii = Var(θ _i ) y Corr(θ _i, θ _j ) = Σ _ij (Σ_ii Σ_jj)^-1/².

Para presentar algunas propiedades de la distribución dada en (1), consideramos la siguiente partición: θ= (θa, θb) ^t , μ y Σ ,y

donde #(A) + #(B) = n. Suponiendo tal partición, algunas propiedades básicas de la distribución normal son:

4 | DEFINICIÓN BÁSICA Y PROPIEDADES DE GMRF

Para construir un GMRF consideramos un grafo 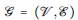con vértices n donde cada vértice representa uno de los componentes del vector θ = (θ ₁ , θ ₂ ,..., θ _n ) y las aristas conectan nodos que tienen algún tipo de asociación. Un GMRF supone que θ = (θ ₁ , θ ₂ ,..., θ _n ) ^T ~ N (μ, Σ) y que las aristas del grafo conectan nodos i y j si y solo si 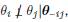, es decir, si θ _i es independiente de θ,, dados los componentes de 6 excepto θ _i y θ,.

Teorema 4.1. Si θ ~ N(μ, q), entonces para i # j,

La demostración se puede encontrar en [⁶]. Por lo tanto, este resultado establece que los componentes no nulos de q determinan la relación de vecindad presente en . Esto implica que cualquier distribución normal con una matriz de covarianza definida positivamente también es un GMRF y viceversa. Por lo tanto, un GMRF se define formalmente de la siguiente manera:

Definición 4.2. Un vector aleatorio θ = (θ ₁ , θ ₂ ,..., θ _n ) ^T є ℝⁿ es llamado GMRF correspondiente a un grafo 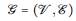con media m y matriz de precisión q > 0, si y solamente si la función de densidad de probabilidad de 6 tiene la siguiente forma:

donde la matriz q cumple la siguiente condición:

Si q es una matriz completamente densa, entonces G está completamente conectado, es decir, el vértice está conectado a todos los demás vértices del grafo. En este artículo, consideramos el caso donde q es esparsa, es decir, la mayoría de las componentes de la matriz son cero.

Teorema 4.3. Sea un grafo 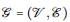que representa 6 un GMRF, con media m y la matriz de precisión q simétrica y definitiva positiva. Luego, la distribución de cada componente 9 _i de 6, dado el vector 6_-i formado por todos los componentes de 6, excepto 9 _i es una distribución normal tal que:

donde i ~ j denota que el nodo j es vecino de nodo i.

5 | ESPECIFICACIÓN DE GMRF A TRAVÉS DE CONDICIONALES COMPLETAS

Una alternativa a la construcción de un GMRF es considerar las condicionales completas de las distribuciones π(θ _i |θ _-i ). Este enfoque pionero se adoptó en ([⁹]) para construir los modelos autorregresivos condicionales, conocidos como modelos CAR. Suponga que la distribución condicional completa de θ _i dada θ _-i para todos i = 1,...,n es una distribución normal con media y precisión dadas respectivamente por:

con k _í > 0, donde la suma en (4) está sobre todos los j de i vecinos. El siguiente teorema nos muestra que esta densidad conjunta de θ existe y que es única.

Teorema 5.1. Si θ _i , dado θ _-i , ∀i = 1,...,n, tiene una distribución normal, con media y precisión dadas en (4) y (5), por lo que la distribución conjunta de θ es un GMRF con vector de medias μ = (μ ₁ , μ ₂ ,…,μ _n ) y matriz de precisión Q, de modo que

en que K _i β _ji , = K _i β _ji , i# j.

La demostración de este resultado se puede encontrar en ([⁶]) y la demostración de los resultados de la aplicación de la Expansión Brook se muestra a continuación y cuya demostración se puede encontrar en ([⁷]).

Teorema 5.2. Si f (θ ₁ | θ _-1 ),f (θ ₂ | θ _-2 ),..., f (θ _n | θ _-n ) son las n distribuciones condicionales completas de una densidad conjunta f (θ) y si x es una configuración de referencia cualquiera tal que f (θ) > 0, entonces la densidad conjunta f (θ) se puede obtener

5.1 | Un ejemplo de Campos de Markov Gaussianos: el modelo CAR

Considere una región geográfica que está dividida en subregiones n indexadas por enteros 1,2,...,n. Suponga que esta colección de subregiones está dotada de un sistema de vecindad {V _i : i: 1,. ..• ,n}, donde V _i denota la colección de subregiones que, en un sentido bien definido, son vecinos de la subregión i. En términos geográficos,

El modelo CAR supone que las distribuciones condicionales completas para efectos aleatorios correspondientes a las variables de respuesta para cada y ₁ ,...,y _n , definidas como θ ₁ , θ _n y dadas por θ - θ _i | θ _-i , i - 1,...,n, siguen distribuciones normales con media y precisión dadas respectivamente en (4) y (5) suponiendo que 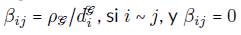caso contrario en que 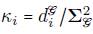, esto es,

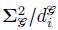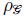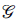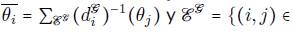
donde es la variante condicional de θ _i |θ _-i , es una constante de proporcionalidad, d ^f es el número de vecinos del nodo i en el grafo , la media de los vecinos del nodo i es 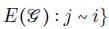es el conjunto de aristas que pertenecen al grafo f. Sea la matriz de adyacencia:

tome 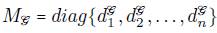. No es inmediato que (7) conduzca a una distribución conjunta completa de θ. [⁹] usa la expansión de Brooky muestra que cuando la matriz ( 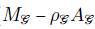) ^-1 es definida positiva y simétrica, la distribución conjunta de 0 es:

donde 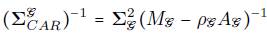. Para que la matriz de covarianza sea definida positiva, es necesario que 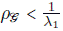donde λ ₁ es el valor propio más pequeño de la matriz 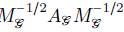. La demostración se puede encontrar en ([¹⁰]).

En resumen, el modelo CAR esta definida por una estructura de correlación inducida por el grafo de la siguiente forma: la región de estudio V se divide en n unidades de área sobre el conjunto de regiones {V _i : i: 1,... ,n} que están vinculados a un conjunto correspondiente de respuestas y - (y ₁ ,y ₂ ,..., y _n ) distribuidas condicionalmente como:

Así, el patrón espacial en la respuesta está modelado por θ. En particular, su uso es fundamental en los modelos bayesianos.

5.2 | Definición de las matrices del modelo CAR en R: División política de Colombia

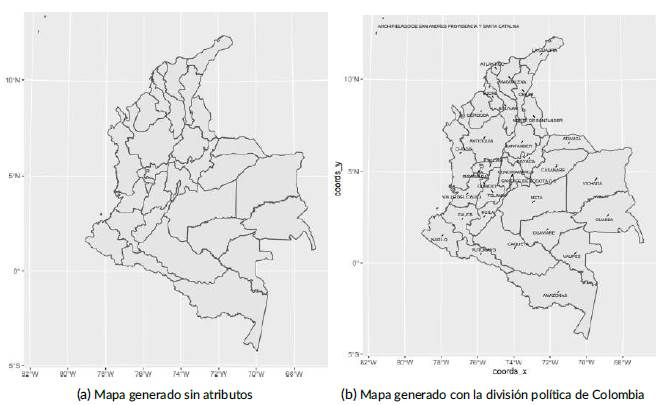
En esta sección se muestra un ejemplo para formular las matrices correspondientes al modelo CAR. Además, se muestra como diseñar estas matrices en R a partir de mapas y, a manera de ejemplo, se utiliza el mapa de Colombia teniendo como base el formato de ggplot2. En primer lugar, se cargan los siguientes paquetes:

Luego, en la internet, se debe buscar el archivo tipo shapefile (.shp) del mapa y los atributos deseados. Por ejemplo, se buscó el mapa de Colombia con la división política en la página web¹ llamado depto.shp. En esta página web, una gran cantidad de mapas de Colombia con diferentes características, incluyendo el mapa con las Fronteras Marinas de Colombia y la División municipal de Colombia, además de otros mapas de Bogotá y Sudamérica. Otras páginas web con descargas libres y con gran cantidad de mapas y atributos de Colombia son: Sistema de Información Ambiental para Colombia, SIAC ² y la página web de los Datos Abiertos de Bogotá a través del ViveLab Bogotá de la Universidad Nacional de Colombia³ entre otras. Después de descargar el archivo .shp, se importa a R con los siguientes comandos:

FIG. 1 Mapa con la división política de Colombia 

El comando st_as_sf convierte un objeto desconocido en un objeto shapefile, para que pueda ser utilizado sin problemas en las funciones del paquete ggplot2. El siguiente comando genera el mapa de Colombia sin atributos (1a).

Otra opción es crear variables asociadas a alguna característica, como sería el caso de asignar los nombres de los departamentos a alguna variable, esto se puede realizar utilizando el comando mutate. Una forma de hacerlo, es generando puntos ubicados en el centro de los unidades, estos puntos se llaman centroides. Para generarlos en R, se crean las variables: centroid, coords, coords_xy coords_y utilizando los siguientes comandos:

Así, la Figura (1b) fue generada con las variables mencionadas anteriormente con ggplot y el paquete ggrepel para generar los textos:

Ahora, para construir la matriz de adyacencia debemos construir el grafo de vecindad de los departamentos de Colombia en el modelo CAR, se consideran como vecinos a cualquier par de departamentos que comparten limite geográfico. Para hacer este grafo, primero se debe guardar las coordenadas de las unidades del mapa con el comando st_centroid:

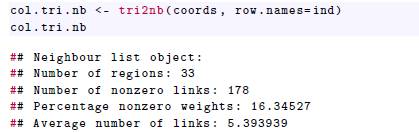
Luego, se debe identificar el conjunto de vecindarios. Los archivos tipo shapef file son objetos usualmente representados por vectores, que consisten en la descripción de la geometría o forma (shape) de los objetos, algunos están descritos por medio de polígonos y otros por multipolígonos, se debe prestar atención a estas características. Si el archivo esta descrito por medio de polígonos, la función que se debe utilizar para generar el conjunto de vecindarios es poly2nb y si el archivo esta descrito por medio de multipolígonos, se debe utilizar tri2nb, ambas funciones pertenecen al paquete spdep. El archivo depto. shp esta descrito por medio de multipolígonos, así:

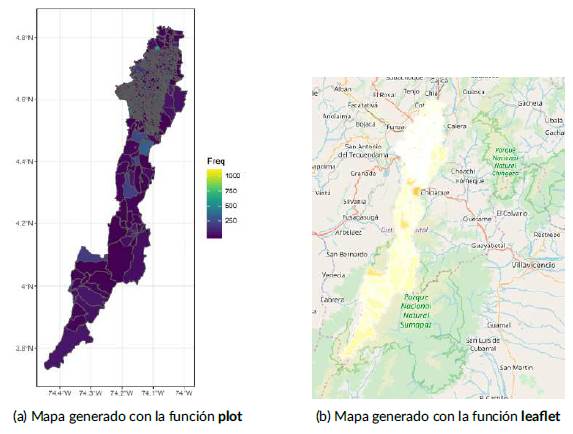
El mapa en la Figura (2) de la división política de Colombia con el grafo de vecindad por adyacencia superpuesto es generado por medio de los siguientes comandos:

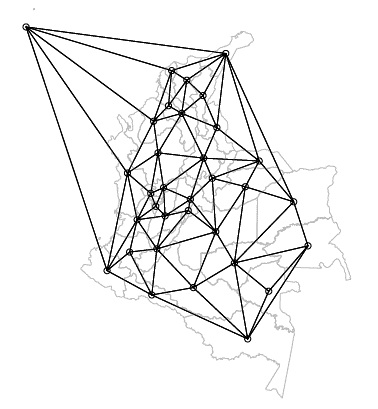
FIG. 2 Mapa de la división política de Colombia con el grafo de vecindad por adyacencia superpuesto. 

Y finalmente, para construir la matriz de adyacencia, la función nb2mat, permite convertir el conjunto de vecindarios en una matriz de adyacencia:

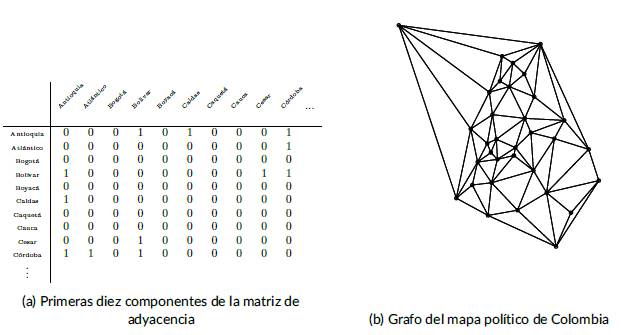
Así, en la Figura (3b) podemos ver el grafo asociado al mapa de Colombia y en la Figura (3a) las primeras diez componentes de la matriz de adyacencia; esta matriz es de tamaño 33 x 33, ya que Colombia se divide administrativa y políticamente en 33 divisiones: 32 departamentos y un distrito capital, Bogotá.

FIG. 3 Matriz de adyacencia y grafo del mapa político de Colombia 

5.3 | Ejemplo modelo CAR en R: hurto de celulares en Bogotá

Para este ejemplo, vamos a suponer que los valores y son el conjunto de datos de hurto de celulares del 01 de enero al 30 de noviembre del año 2018, estos fueron descargados de la página web de Datos Abiertos de Bogotá a través del ViveLab Bogotá de la Universidad Nacional de Colombia⁴, el archivo se llama "scat. shp" y es importado a R por medio de los siguientes comandos:

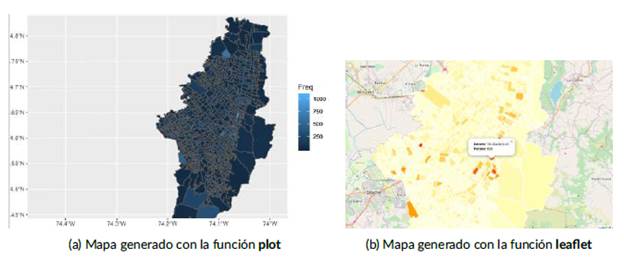
La base de datos contiene el número de hurtos de celulares en cada uno de los 1168 barrios de Bogotá. Para graficar estos datos se propone dos métodos, uno con el comando propio de R y el otro con el paquete leaf let. El siguiente código genera la Figura 5a.

Leaflet es una biblioteca JavaScript de código abierto muy popular para mapas interactivos. Se puede crear un mapa usando Leaflet llamando a la función Leaflet() y luego agregando capas al mapa usando funciones de capa, llamadas layer. Por ejemplo, podemos usar addTiles() para agregar un mapa de fondo, addPolygons() para agregar polígonos y addLegend() para agregar una leyenda. Podemos emplear una variedad de mapas de fondo.

Se puede crear el mapa de Bogotá con una escala de colores dada por la paleta "YlOrRd" del paquete RColorBrewer de la siguiente manera. Primero, transformamos el mapa al formato requerido por el paquete Leaflet(), hacemos esto usando la función st_transform() del paquete sf. En las Figuras (5a) y (5b) se presentan los mapas generados de Bogotá con las funciones descritas anteriormente y en las Figuras (4a) y (4b) se presenta los mismos mapas pero centrados en la zona urbana de Bogotá.

FIG. 4 Distribución de hurtos de celulares en el centro Bogotá 

Antes de empezar a realizar el análisis con el modelo CAR, se puede calcular una medida de autocorrelación espacial. La estadística más utilizada para identificar autocorrelación espacial es el índice de Moran desarrollado por Patrick Alfred Pierce Moran, ([⁹]). Esta estadística es utilizada para realizar un test que permite evaluar la significancia de la correlación espacial bajo la hipótesis nula de que hay cero autocorrelación espacial presente en la variable. Este test de Moran creará una medida de correlación entre -1 y 1 en donde 1 determina una correlación espacial positiva perfecta 0 significa que nuestros datos están distribuidos aleatoriamente y -1 representa autocorrelación espacial negativa. En R, la implementación es muy sencilla, utilizando el comando moran.test. Para esto debemos generar un objeto de tipo listw (matriz de pesos):

El estadístico I de Moran confirma la existencia de autocorrelación espacial positiva en la distribución de hurtos de celulares. En efecto, con un valor estimado de 0.1530 y un p-valor de 2.2e - 16, debe rechazarse la hipótesis de aleatoriedad espacial y aceptar la presencia de autocorrelación espacial positiva. También nos muestra que existe una leve relación de correlación positiva, versus una expectativa de una leve relación negativa.

FIG. 5 Distribución de hurtos de celulares en Bogotá 

Así, con la evidencia estadístico I de Moran, se aplica el modelo CAR. Como no se considera variables regresoras, el modelo apenas va a describir el comportamiento espacial bajo el supuesto de que el número de hurtos se distribuye Normal. De la misma forma que en el mapa de Colombia, se genera el grafo y la matrices correspondientes para utilizar el modelo CAR. Así, con estos valores ajustamos el modelo:

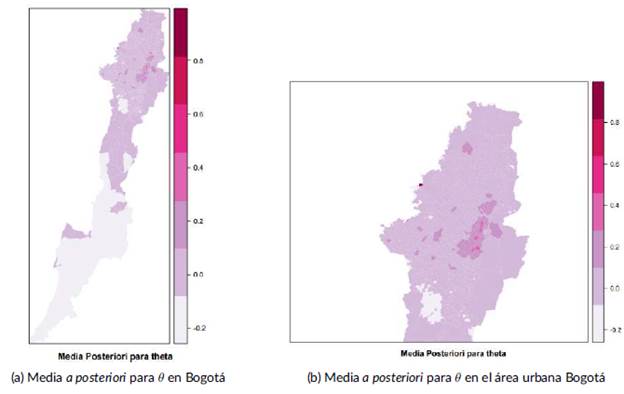
y utilizando métodos MCMC se estima los parámetros 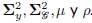. En este artículo profundiza en este tema, pero se puede encontrar estos métodos en ([⁷]) o ([¹⁰]). En las Figuras (6a) y (6b )se presenta la media de los efectos aleatorios θ a posteriori.

FIG. 6 Media a posteriori para 6 en Bogotá 

La estimación a posteriori de los valores de θ mostrados en las Figuras (6a) y (6b) nos muestra un resultado relevante y es que existe evidencia de una autocorrelación espacial, esto es, el número de robos de celulares de Bogotá está asociado con elvecindario. Además, muestra que la variable se puede modelar siguiendo una distribución normal, ya que esta describe el comportamiento espacial mostrando valores de 0 mayores en la zona del centro de Bogotá, donde existe un mayor número de hurtos de celulares.

Conclusión

Este documento contiene una descripción estadística de los hurtos de celulares registrados en los barrios de Bogotá, mostrando que existe dependencia espacial. Se mostró también como se pueden realizar estos análisis en R, presentando los comandos y los paquetes que pueden ser empleados para este tipo análisis. La idea es que las personas puedan utilizar estas herramientas en sus propios estudios, así como descargar información de internet, mapas, datos, ya que todo esto se encuentra disponible. Se efectúa la ubicación espacial de cada delito sobre el mapa de Bogotá: las mayores concentraciones delictivas se presentan con mayor intensidad en el centro de Bogotá y en algunos barrios al sur de la ciudad.

Sin embargo, este es apenas un análisis descriptivo, como complemento de las cifras de criminalidad, se puede considerar variables regresoras que expliquen el comportamiento de hurtos de celulares. También se puede cambiar la distribución para la variable respuesta a una más adecuada, como la distribución Poisson, que podría ajustarse mejor al modelo. Todos estos análisis se pueden realizar por medio del uso del modelo CAR con una extensión natural modelando la media por medio de variables regresoras y cambiando la distribución Normal por una distribución Poisson.