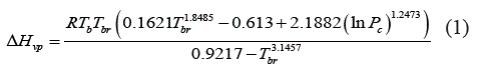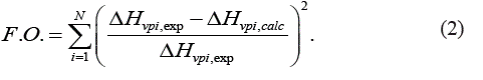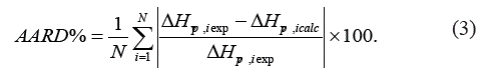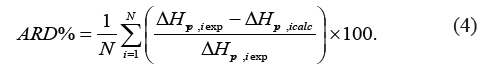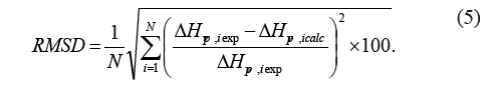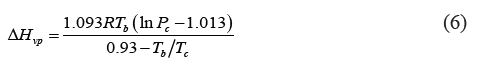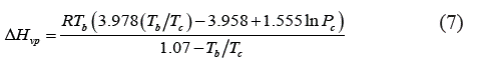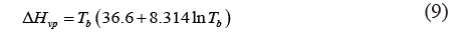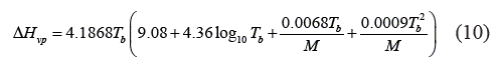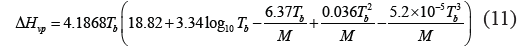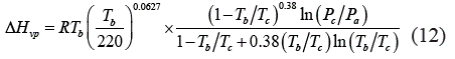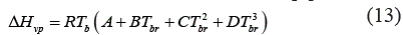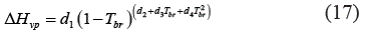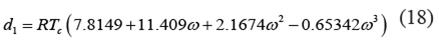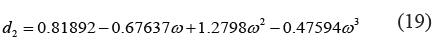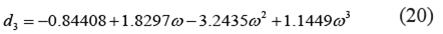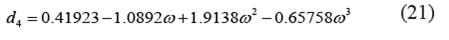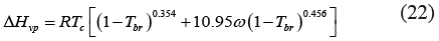I. INTRODUCCIÓN
La entalpía de vaporización se define como la diferencia entre las entalpías de fase de vapor y líquido a la misma temperatura y presión, por otro lado la entalpía de vaporización (ΔH vp ) es la cantidad de energía que es requerida para transformar un material a una temperatura especificada desde la fase líquida a la fase de vapor [1].
El conocimiento de la entalpía de vaporización es de gran importancia en ingeniería ya que permite simular, diseñar y optimizar procesos que involucren cambios de fase líquido-vapor como destilación, evaporación o secado [2,3]. Para mejorar las simulaciones numéricas es necesario el uso de correlaciones termodinámicas precisas, es el caso del calor de vaporización en la predicción de equilibrios líquido-vapor en múltiples etapas de sistemas multicomponentes, ya que éste controla la temperatura y los perfiles de líquido y vapor en una columna [4]. Por tal motivo, existe un gran interés en ingeniería en la medición y correlación de los valores de esta propiedad [5].
La entalpía de vaporización de fluidos puros se puede calcular utilizando ecuaciones de estado o de una manera más simple por medio de correlaciones empíricas, algunas de estas solo requieren las propiedades del fluido como temperatura crítica, presión crítica, temperatura normal de ebullición, peso molecular, factor acéntrico, entre otros [2].
Diferentes ecuaciones para el cálculo de la entalpía normal de vaporización están reportados en la literatura científica, los más conocidos son: Riedel [6],Chen [7], Trouton [8], Zhao et al. [9], Vetere [10], Liu [11], Mehmandoust et al. [5], Morgan, Carruth y Kobayashi [12], Sivaraman et al., Faúndez et al. [2].
Vetere desarrolló una correlación empírica para el cálculo de la entalpía de vaporización para hidrocarburos y alcoholes que depende de dos variables: el peso molecular y la temperatura, con desviaciones menores al 2.08% [10], mientras que la ecuación de Chen depende de la temperatura normal de ebullición, temperatura crítica, presión crítica con desviaciones promedio del 1.82%[7], por otro lado el modelo propuesto por Mehmandoust et al., depende de tres variables: presión crítica, temperatura crítica, temperatura normal de ebullición con 10 constantes y desviaciones promedio del 2.74% [5].
Se propone en este estudio un nuevo modelo simple y generalizado para el cálculo de la entalpía de vaporización de sustancias puras a partir del conocimiento de la temperatura normal de ebullición y de las propiedades críticas: temperatura crítica y presión crítica. Finalmente, la ecuación generalizada se compara con diferentes modelos reportados en la literatura científica.
II. NUEVA ECUACIÓN PROPUESTA Y FUNCIÓN OBJETIVO
La ecuación (1) representa el modelo empírico propuesto para el cálculo del calor de vaporización.
Donde (H vp es la entalpía de vaporización, R es la constante universal de los gases (8.3145 Jmol-1K-1), T b es la temperatura normal de ebullición en K, T c es la temperatura crítica en K, T br es la temperatura normal de ebullición reducida, calculada como T br =T b /T c y P c es la presión crítica en bar.
Se realiza una búsqueda de los valores de presión crítica, temperatura crítica, factor acéntrico, temperatura normal de ebullición y datos experimentales del calor de vaporización de 527 sustancias puras que se analizarán en la presente investigación [13-18]. Se determinaron las constantes de la ecuación (1), utilizando el algoritmo propuesto por Lasdon et al. [19], y la función objetivo dada por la ecuación (2) para 300 sustancias puras.
La función objetivo a minimizar representa la suma de los cuadrados de las diferencias entre los valores experimentales y los valores del nuevo modelo, donde N es el número de compuestos, (H vpi,exp es el calor de vaporización experimental y (H vpi,calc son los valores calculados por el modelo.
Se evalúa la generalización del modelo propuesto por medio del porcentaje de error promedio estándar (AARD%), porcentaje de desviación relativa (ARD%), y la desviación de la raíz cuadrada media (RMSD) [20].
III. COMPARACIÓN DE DIFERENTES MODELOS PARA EL CÁLCULO DE LA ENTALPÍA DE VAPORIZACIÓN
Se compararon los resultados obtenidos con ecuaciones para el cálculo de la entalpía de vaporización, entre las que se destacan:
a. Modelo de Riedel [6]:
Donde (H vp es la entalpía de vaporización, R es la constante universal de los gases (8.3145 Jmol-1K-1), T b es la temperatura normal de ebullición en K, T c es la temperatura crítica en K y P c es la presión crítica en bar.
b. Ecuación de Chen [7]:
c. Regla de Trouton [8]:
d. Modelo de Zhao et al. [9]:
e. Ecuación de Vetere [10]:
Para hidrocarburos:
Para alcoholes:
Donde M es el peso molecular en kgkmol-1.
f. Ecuación de Liu [11]:
Donde P a es la presión atmosférica en bar.
g. Ecuación de Mehmandoust et al. [5]:
Las constantes A, b 1 , b 2 , b 3 , c 1 , c 2 , c 3 , d 1 , d 2 , d 3 estan reportadas en la Tabla I.
TABLA I CONSTANTES DEL MODELO DE MEHMANDOUST ET AL.
| Coeficientes | Valores |
| A | 0.01290 |
| b1 | 0.00086 |
| b2 | -0.00206 |
| b3 | 0.01150 |
| c1 | -0.01983 |
| c2 | 0.00632 |
| c3 | -0.04279 |
| d1 | 0.02086 |
| d2 | -0.00459 |
| d3 | 0.03544 |
a. Ecuación de Morgan [12]:
Donde ϖ es el factor acéntrico.
b. Ecuación de Carruth y Kobayashi [12]:
VI. RESULTADOS Y DISCUSIÓN
A partir del conocimiento de la temperatura normal de ebullición, temperatura crítica y presión crítica de 300 sustancias puras, se determinaron las constantes de la nueva ecuación utilizando el algoritmo de Lasdon et al., el cual minimiza la suma de los cuadrados de las desviaciones relativas de la entalpía de vaporización.
En la Tabla II, se presenta un resumen estadístico de las 300 sustancias puras sometidas al proceso de minimización por medio del porcentaje de error promedio estándar (AARD%), porcentaje de desviación relativa absoluta (ARD%), y la desviación de la raíz cuadrada media (RMSD).
TABLA II PARÁMETROS ESTADÍSTICOS EVALUADOS EN 300 SUSTANCIAS PURAS EN COMPARACIÓN CON OTROS MODELOS.
| AARD% | ARD% | RMSD | |
| Nuevo Modelo | 0.1059% | 0.0033% | 0.0041 |
| Riedel | 0.9776% | 0.6235% | 0.0579 |
| Chen | 0.5227% | -0.2334% | 0.0084 |
| Trouton | 7.2017% | 0.4897% | 0.1450 |
| Zhao et al. | 6.4356% | -3.0795% | 0.0848 |
| Vetere | 13.7068% | 13.9984% | 0.0858 |
| Liu | 2.1062% | -0.9235% | 0.0235 |
| Mehmandoust et al. | 3.1377% | -3.0958% | 0.6340 |
| Morgan | 3.8542% | 4.8187% | 0.0326 |
| Carruth y Kobayashi | 1.4814% | -1.7180% | 0.0113 |
De la Tabla II la ecuación propuesta en la investigación presenta el menor porcentaje de error relativo (AARD%) del 0.1059%, en comparación con otros modelos evaluados en el presente artículo. También se observa que la magnitud global de los valores de RMSD es de relativo bajo orden de magnitud (≤ 0.0041), por lo cual se establece que los resultados simulados utilizando el modelo propuesto se ajustan razonablemente a los valores encontrados experimentalmente, validándose así dicho modelo.
La ecuación de Vetere genera porcentajes de desviación relativa del 13.7068%, resultados que están conformes a lo reportado por Tatar et al., quienes reportan desviaciones del 69.70% [3], mientras que la ecuación de Trouton en el presente trabajo generó desviaciones del 7.2017%, resultado que ésta de acuerdo a lo reportado por Mehmandoust et al. [5].
En la Tabla III, se muestra el porcentaje de error promedio estándar (AARD%) del modelo propuesto y diferentes ecuaciones para el cálculo de la entalpía de vaporización.
TABLA III PORCENTAJE DE ERROR PROMEDIO ESTÁNDAR (AARD%) DE LOS VALORES OBTENIDOS POR LA NUEVA ECUACIÓN, EN COMPARACIÓN CON OTROS MODELOS DE ENTALPÍA DE VAPORIZACIÓN.
| Número de Compuestos | Nuevo Modelo | Riedel | Chen | Trouton | Zhao et al. | Vetere | Liu | Mehmandoust et al. | Morgan | Carruth y Kobayashi | |
| Alcanos | 10 | 0.215% | 1.265% | 0.634% | 9.037% | 2.529% | 15.891% | 1.625% | 3.949% | 4.016% | 1.511% |
| Alquenos | 31 | 0.018% | 0.403% | 0.231% | 7.005% | 2.377% | 15.264% | 0.904% | 2.790% | 1.989% | 0.969% |
| Alquinos | 4 | 0.008% | 0.797% | 0.525% | 2.801% | 5.819% | 13.910% | 1.600% | 1.065% | 2.147% | 0.660% |
| Hidrocarburos cíclicos | 7 | 0.012% | 0.629% | 0.388% | 4.666% | 1.108% | 14.489% | 1.383% | 1.519% | 1.845% | 0.614% |
| Aromáticos | 29 | 0.015% | 0.792% | 0.321% | 2.835% | 4.227% | 13.047% | 1.169% | 1.136% | 3.178% | 1.202% |
| Alcoholes y éteres | 33 | 0.079% | 1.612% | 0.794% | 12.138% | 13.888% | 10.924% | 4.103% | 5.242% | 7.291% | 2.350% |
| Aldehídos y cetonas | 20 | 0.021% | 0.818% | 0.380% | 3.102% | 5.001% | 13.252% | 1.428% | 1.408% | 3.514% | 1.566% |
| Esteres | 8 | 0.017% | 0.897% | 0.400% | 3.831% | 5.585% | 13.108% | 1.769% | 2.635% | 5.130% | 2.187% |
| Hidrocarburos halogenados | 95 | 0.020% | 0.672% | 0.378% | 3.898% | 3.980% | 13.947% | 1.598% | 1.673% | 3.099% | 1.247% |
| Compuestos azufrados | 6 | 1.764% | 4.520% | 1.462% | 31.890% | 28.800% | 19.494% | 9.611% | 6.671% | 10.142% | 2.991% |
| Compuestos nitrogenados | 9 | 0.081% | 0.920% | 0.572% | 8.984% | 9.199% | 12.768% | 2.402% | 2.713% | 3.714% | 1.325% |
| Gases Nobles | 6 | 0.111% | 1.035% | 0.903 | 18.201% | 1.750% | 17.363% | 2.627% | 6.422% | 1.779% | 1.589% |
| Compuestos inorgánicos | 19 | 0.576% | 1.781% | 1.903% | 16.748% | 10.900% | 14.749% | 3.704% | 107.602% | 3.428% | 1.801% |
| Ácidos orgánicos | 23 | 0.028% | 1.221% | 0.509% | 7.654% | 9.477% | 12.037% | 2.493% | 4.041% | 5.579% | 2.036% |
| Promedio | 300 | 0.2104% | 1.2175% | 0.635% | 9.508% | 7.496% | 14.306% | 2.550% | 3.704% | 4.035% | 1.546% |
A partir de la Tabla III el AARD% muestra que el nuevo modelo representa un buen ajuste para todos los tipos de compuestos analizados, a excepción de los compuestos azufrados con desviaciones menores al 1.764%.
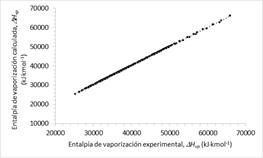
La Fig. 1 muestra la comparación de las entalpías de vaporización experimental y los predichos por el nuevo modelo, donde éste presenta una gran predicción de los datos experimentales con un coeficiente de correlación del 0.9995.
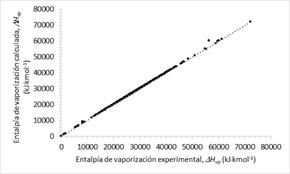
Fig. 1 Exactitud del nuevo modelo propuesto frente a los datos experimentales de 300 sustancias puras.
En la Fig. 2 se evidencia el porcentaje de desviación relativa absoluta (ARD%) frente a la entalpía de vaporización calculada por el nuevo modelo y se concluye que las desviaciones se encuentran entre -0.40% y 1.6% demostrando así la precisión en describir los datos experimentales.
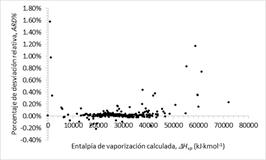
Fig. 2 Porcentaje de desviación relativa Vs. la entalpía de vaporización calculada por el nuevo modelo de 300 sustancias puras.
Con el fin de validar el modelo propuesto se evaluaron 227 sustancias, puras, las cuales no participaron en la minimización. Los valores de temperatura crítica, presión crítica, temperatura normal de ebullición y factor acéntrico, son tomados de la literatura científica [13-16].
En la Tabla IV se presenta un resumen estadístico de las 227 sustancias puras que no fueron sometidas al proceso de minimización, entre las que se destacan compuestos azufrados, cetonas, esteres, alcoholes, hidrocarburos halogenados, alcanos, alquenos, ácidos orgánicos, alquinos, hidrocarburos cíclicos, aromáticos, aldehídos, compuestos nitrogenados, compuestos inorgánicos.
TABLA IV PARÁMETROS ESTADÍSTICOS EVALUADOS EN 227 SUSTANCIAS PURAS EN COMPARACIÓN CON OTROS MODELOS.
| AARD% | ARD% | RMSD | |
| Nuevo Modelo | 0.0821% | 0.0351% | 0.00096 |
| Riedel | 0.9442% | 0.9430% | 0.00833 |
| Chen | 0.6116% | -0.6030% | 0.00488 |
| Trouton | 5.1653% | -1.1842% | 0.04174 |
| Zhao et al. | 4.5431% | -2.3011% | 0.03874 |
| Vetere | 14.0812% | 14.0812% | 0.09402 |
| Liu | 1.8406% | -1.2723% | 0.01586 |
| Mehmandoust et al. | 2.8550% | -0.6645% | 0.02314 |
| Morgan | 5.9337% | 5.9337% | 0.04452 |
| Carruth y Kobayashi | 2.4455% | -2.4455% | 0.01692 |
Los resultados presentados en la Tabla IV están conformes a lo reportado por Tatar et al. [3], Mehmandoust et al. [5], Kikic y Vetere [21], Sanjari et al. [12], Cachadiña y Mulero [2].
Los resultados demuestran la superioridad en la predicción que tiene el nuevo modelo desarrollado para el cálculo de la entalpía de vaporización en comparación con ecuaciones reportadas en la literatura científica con desviaciones promedio del 0.0821%. De la Tabla IV el valor de RMSD es de relativo bajo orden de magnitud (≤ 0.00096) y se establece que los resultados simulados, utilizando el modelo propuesto, se ajustan a los valores encontrados experimentalmente, validándose de nuevo el modelo.
La Fig. 3 muestra la comparación de las entalpías de vaporización experimental y los predichos por el nuevo modelo y se concluye que éste presenta gran precisión en la predicción de los datos experimentales, con un coeficiente de correlación de 0.9999.
En la Fig. 4 se evidencia el porcentaje de desviación relativa absoluta (ARD%), frente a la entalpía de vaporización calculada por el nuevo modelo para las 227 sustancias que no participaron en la minimización, en donde las desviaciones varían desde -0.03% a 0.98%.
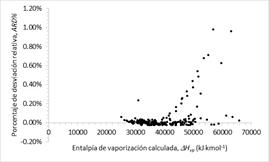
Fig. 4 Porcentaje de desviación relativa versus la entalpía de vaporización calculada por el nuevo modelo de 227 sustancias puras.
El modelo desarrollado en la presente investigación se empleará en diferentes procesos industriales [2,3,22] y en educación en ciencias básicas [23,24].
V. CONCLUSIONES
El nuevo modelo generalizado objeto de estudio en el presente artículo, calcula la entalpía de vaporización y presenta porcentajes de error promedio estándar para 300 sustancias puras de 0.1059% y porcentajes de desviación relativa absoluta entre -0.40% a 1.60%, mientras que para 227 sustancias que no participaron en el proceso de minimización genera porcentajes de error promedio estándar de 0.0821% y porcentaje de desviación relativa absoluta entre -0.03% a 0.98%.
Diferentes métodos para predecir la entalpía de vaporización fueron comparados y evaluados para una sustancia en particular. Se encuentran errores de predicción aceptables, usando las ecuaciones de Riedel, Chen, Trouton, Zhao et al., Vetere, Liu, Mehmandoust et al., Morgan, Carruth y Kobayashi, sin embargo, la nueva ecuación propuesta genera la menor desviación del 0.0821% de las 527 sustancias puras analizadas en la presente investigación.