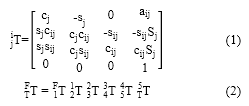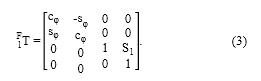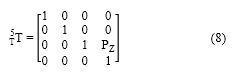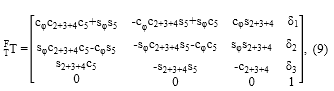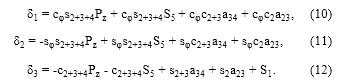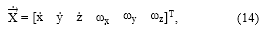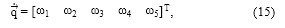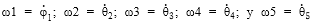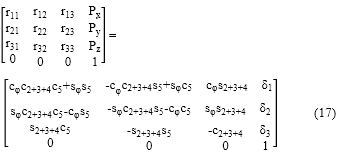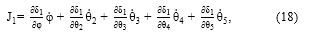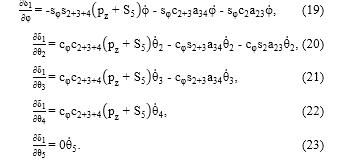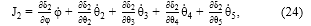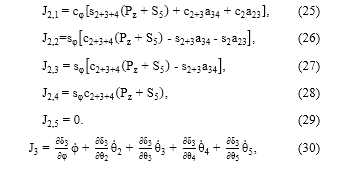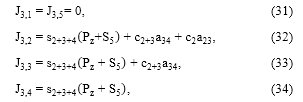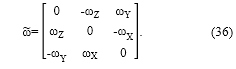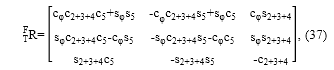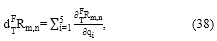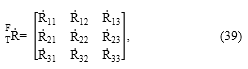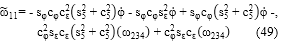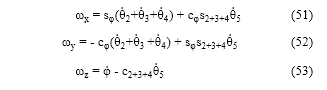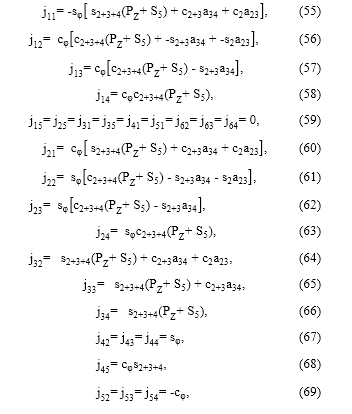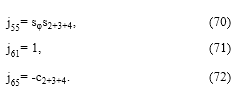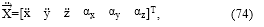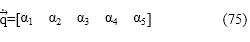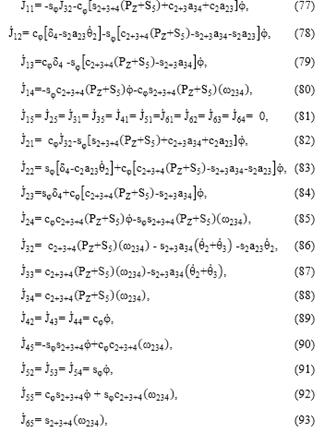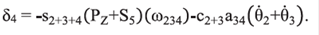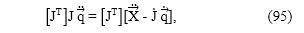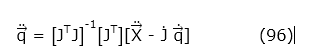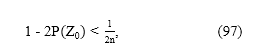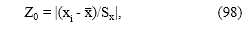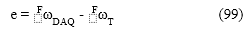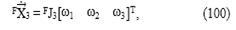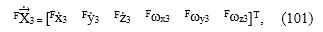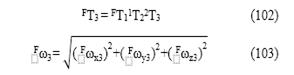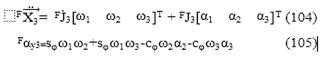I. INTRODUCCIÓN
La implementación de robots en la industria se remonta a principios de la década de los 60, gracias a J. Engelberger con la creación de los robots tipo Unimate [1] de la compañía Unimation Inc., los cuales fueron utilizados en la industria automotriz para el manejo de las máquinas de fundición a presión [2]. Posteriormente, Unimation introduce a finales de los 70 la serie de robots llamados PUMA (Programmable Universal Machine for Assembly), usados en aplicaciones de montaje y armado de piezas. Manipuladores seriales tipo SCARA [3], los modelos KUKA y Mitsubishi Movemaster han sido usados en las últimas décadas en tareas repetitivas o en ambientes de alto riesgo como la soldadura, pintura y el manejo de material radiactivo [4]. Entre estos se destacan productores como ABB, KUKA y FANUC [5].
El modelo RV-M1 de Mitsubishi, debido a su versatilidad, ha sido implementado en diversos sectores industriales [6] y educativos [7-9] donde se destaca como material didáctico y elemento de prueba en las investigaciones [5-10]. Con el fin de mejorar su funcionamiento, se desarrolla la formulación matemática completa de su cinemática de velocidad y aceleración [1]. La cinemática de velocidad y la cinemática de aceleración, al igual que la de posición, puede ser directa o inversa [1-11], y en ambos casos las variables, es decir las velocidades y aceleraciones de herramienta y juntas, se relacionan a través de la matriz Jacobiano, cuyos elementos son los coeficientes que resultan de derivar una función multivariable [12-15]. Para el caso de la cinemática directa de velocidad y aceleración se debe expresar el estado de velocidad y aceleración del efector final o herramienta en función de las velocidades y aceleraciones angulares de las juntas actuadas, mientras que en la cinemática inversa se expresan las velocidades y aceleraciones de las juntas actuadas en función del estado de velocidad y aceleración del efector final [13].
Se desarrolla el modelo cinemático tanto de velocidad como de aceleración, directo e inverso, del robot Mitsubishi Movemaster RV-M1. La nomenclatura de los elementos del robot sigue la notación unificada en [11], y la cinemática directa de posición sigue la notación matricial propuesta por los mismos autores. En cuanto a la cinemática inversa, se adoptará el método propuesto en [10]. Se debe tener en cuenta en la cinemática de posición las limitaciones físicas del robot, escogiendo de las dos posibles soluciones matemáticas la opción que cumpla con el rango operativo del robot [7-16]. Se procede a encontrar analíticamente la matriz Jacobiano para relacionar velocidades de juntas y herramientas. Puesto que el robot Movemaster RV-M1 es un robot inferior [1-2], esta matriz no será cuadrada y se deberá convertir en tal utilizando la matriz traspuesta del Jacobiano; esto permitirá desarrollar la cinemática inversa de velocidad. El paso siguiente a desarrollar será la cinemática de aceleración, para lo cual se toma la derivada de la ecuación de velocidad del robot.
Los resultados del modelo propuesto fueron verificados con el comportamiento real del manipulador en una tarea cinemática. La medición de las velocidades angulares de cada articulación del manipulador se realizó por medio de un sistema de adquisición de datos, construido específicamente para medir velocidad angular [17], mientras los cálculos teóricos se realizaron programando en el software Matlab las ecuaciones determinadas analíticamente [18-19]. El análisis propuesto permitirá expandir las aplicaciones del robot Movemaster RV-M1 en la industria y la academia, puesto que se podrá relacionar posteriormente con el análisis cinemático de posición del robot [10] y con su análisis dinámico [20] para la implementación de leyes de control especializadas.
II. DESCRIPCIÓN DEL ROBOT RV-M1
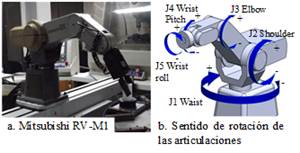
El robot Movemaster RV-M1 es un robot serial tipo vertical, Fig. 1a, de 5 grados de libertad resultantes de igual número de articulaciones tipo junta de revoluta (J1 a J5 en la Fig. 1b) accionadas por motores DC. La capacidad máxima de carga de 1.2 kgf y la velocidad máxima en el extremo de la muñeca (cuarto eslabón) de 1000 mm/seg [16].
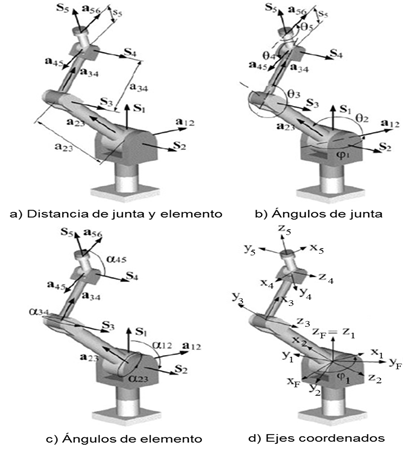
Los parámetros cinemáticos del robot RV-M1 permiten una manera sistemática de relacionar la posición, orientación, velocidad y aceleración de la herramienta con las juntas. Estos se definen de acuerdo a la notación planteada en [11]. Se especifican seis parámetros: dos vectores, dos distancias y dos ángulos derechos, Fig. 2, y son explicados a continuación.
Vector de articulación S i : vector unitario que define el sentido de rotación de una junta de revoluta, se ubica en el eje de rotación de la articulación. El robot Mitsubishi RV-M1 tiene 5 juntas revoluta y 5 vectores de articulación son de este tipo.
Vector del elemento a ij : vector unitario perpendicular a los vectores de articulación Si y Sj con sentido i-j. Define la dirección del eslabón o elemento.
Distancia de articulación Si: distancia entre vectores de elemento a hi y a ij , medida a lo largo del vector S i .
Distancia del elemento aij: distancia a lo largo del vector del elemento a ij , medida entre los vectores de articulación S i y S j .
Ángulo de junta θi: ángulo entre los vectores de elemento a hi y a ij medido mediante la regla de la mano derecha usando como base al vector de articulación Si.
Ángulo del elemento αij: ángulo entre los vectores de articulación S i y S j medido mediante la regla de la mano derecha usando como base al vector de elemento a ij .
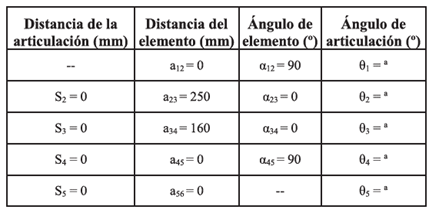
La Tabla I presenta los valores de los parámetros del robot, incluyendo los de valor cero y aquellos variables, de acuerdo con la posición de la herramienta. De la Fig. 2d, cada articulación en el robot tiene un sistema coordenado asociado, de modo que los vectores de articulación y elemento coincidirán con los ejes zi y xi, respectivamente, en cada sistema coordenado. El eje yi se determina mediante la regla de la mano derecha (Si x aij). Un sistema de referencia extra es definido, el marco fijo, denotado como xF-yF-zF en la Fig. 2d.
Se establece la matriz de transformación 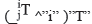 [6], entre dos elementos consecutivos i y j, mediante (1), donde cj = cos(θj), sj = sin(θj), cij = cos(αij) y sij = sin(αij). La matriz en (1) encierra la información de la traslación en las posiciones (1,4), (2,4) y (3,4); y de la orientación en los elementos (1,1) a (3,3). La cuarta fila es de aumento, para convertir la matriz en cuadrada y facilitar los cálculos. A la matriz de transformación que relaciona el sistema coordenado final con respecto al fijo; pasando por todas las articulaciones, se le conoce como matriz de transformación total [11]. Esta resulta de multiplicar las matrices de transformación que relacionan cada elemento con el anterior, como se muestra en (2). La programación de la cinemática de posición se basó en el trabajo presentado en [10].
[6], entre dos elementos consecutivos i y j, mediante (1), donde cj = cos(θj), sj = sin(θj), cij = cos(αij) y sij = sin(αij). La matriz en (1) encierra la información de la traslación en las posiciones (1,4), (2,4) y (3,4); y de la orientación en los elementos (1,1) a (3,3). La cuarta fila es de aumento, para convertir la matriz en cuadrada y facilitar los cálculos. A la matriz de transformación que relaciona el sistema coordenado final con respecto al fijo; pasando por todas las articulaciones, se le conoce como matriz de transformación total [11]. Esta resulta de multiplicar las matrices de transformación que relacionan cada elemento con el anterior, como se muestra en (2). La programación de la cinemática de posición se basó en el trabajo presentado en [10].
Conceptualmente, es posible ubicar el origen del marco fijo en cualquier punto sobre el eje ZF en la Fig. 4d, luego, cuando la primera articulación se acciona el cambio entre el primer sistema coordenado y el marco fijo no es más que la rotación de φ grados alrededor del eje Z. La distancia S1 (distancia entre orígenes) se mantendrá constante. Al aplicar (1) se toma en consideración que el ángulo de elemento αF1 = 0°. Por lo tanto,
Para la segunda matriz de transformación se tiene que el segundo sistema coordenado rota alrededor del eje X una amplitud fija, dando como resultado el ángulo de elemento α12 = 90°, además, al actuar la articulación número 2 se tendrá una rotación θ2 alrededor del eje Z2,
Debido a la estructura del manipulador los ejes Z de los sistemas coordenados 2, 3 y 4 permanecen paralelos sin importar la posición de este, por lo que los ángulos de elemento α23, α34 = 0°, pero presentan desplazamiento del origen del sistema coordenado en la dirección de los vectores de elemento propios de cada sistema, obteniéndose las matrices (5) y (6).
El sistema coordenado 5 presenta una rotación fija en el ángulo de elemento α34 = 90°, y el actuar de la articulación brinda una rotación alrededor del eje Z5 una amplitud θ5, por lo tanto, la matriz (7) tendrá la misma forma de (4):
Finalmente se relaciona el extremo de la herramienta con el origen del sistema coordenado 5 mediante un desplazamiento correspondiente a la longitud de la herramienta en la dirección del vector de articulación 5.
Se reemplazan (3) a (8) en (2) para obtener la matriz de transformación de la herramienta del Mitsubishi RV-M1 en el marco fijo [10]:
Donde c2+3+4 = cos (θ2 + θ3 + θ4), s2+3+4 = sin (θ2 + θ3 + θ4),
Si se conocen los ángulos de posición de los eslabones (φ1, θ2, θ3, θ4, θ5) es posible hallar el lado derecho de (9) para establecer la posición y la orientación de la herramienta del robot en el marco fijo, esta es la cinemática directa. Por el contrario, si se tienen la posición y orientación de la herramienta en el marco fijo, los ángulos de posición de los eslabones se extraen de los términos de la matriz del lado derecho de (9). El artículo de la referencia [10] detalla tales procedimientos, los cuales fueron empleados en la programación de la cinemática de posición.
III. CINEMÁTICA DE VELOCIDAD DEL ROBOT RV-M1
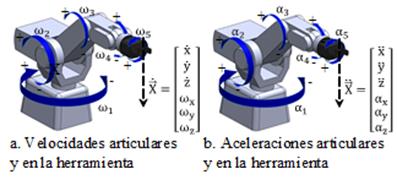
La cinemática de velocidad relaciona las velocidades de las juntas o articulaciones con la velocidad en la herramienta, Fig. 3a. El robot Mitsubishi es un manipulador serial de 5 juntas de revoluta, por lo cual tanto la velocidad lineal como la velocidad angular de la herramienta del robot, con respecto al sistema coordenado global resulta de la composición de las velocidades angulares de los eslabones de la cadena cinemática [1].
A. Cinemática directa de velocidad
En la cinemática directa de velocidad se conocen las velocidades angulares de cada articulación y se pretende determinar la velocidad lineal y orientación que la herramienta adquiere debido a estas. La ecuación que rige la cinemática directa de velocidad está dada por
donde X es el vector estado de velocidad del efector final, dado por
cuyos tres primeros elementos representan la velocidad lineal de la herramienta a lo largo de los ejes Cartesianos ( x : velocidad lineal a lo largo del eje x, y : velocidad lineal de la herramienta a lo largo del eje y, z : velocidad lineal de la herramienta a lo largo del eje z), y los tres últimos elementos del vector en (14) representan las velocidades angulares alrededor de los ejes globales X, Y, y Z, denotadas por ωx, ωy y ωz, respectivamente; q es el vector de velocidad angular de juntas dado por
Con
representando las velocidades angulares de las juntas o razones de cambio de los ángulos; y J es la matriz Jacobiano del robot que permite la transformación del vector de juntas actuadas al estado de velocidad de la herramienta.
A partir de (13) se infiere el problema de la cinemática directa del robot: Conocidos: cinemática de posición (ángulos de junta y posición y orientación de la herramienta) y el vector de velocidad angular de juntas q , halle el estado de velocidad de la herramienta X . La misma ecuación (13) es la solución a este problema, siempre y cuando se conozca la matriz Jacobiano, J.
B. Cinemática inversa de velocidad
El problema de la cinemática inversa de velocidad del robot se establece a continuación. Conocidos: cinemática de posición (ángulos de junta y posición y orientación de la herramienta) y el vector estado de velocidad de la herramienta X , halle el vector de velocidad angular de las juntas q .
Ahora se desea conocer el vector de velocidades angulares q , a partir del conocimiento del estado de velocidad de la herramienta, es decir, X . La solución a este problema se presenta a continuación. A partir de (14) se nota que el vector de velocidad del efector final es de tamaño 6x1, y de (15) es aparente que el tamaño del vector de velocidad de juntas es tamaño 5x1, por lo cual la matriz Jacobiano del Mitsubishi RV-M1 es no cuadrada, lo cual impide el despeje directo de q a partir de (13) mediante la premultiplicación a ambos lados por la matriz inversa del Jacobiano, es decir J-1. Para resolver este inconveniente se utiliza el método de la traspuesta del Jacobiano [2-13].
El método de la transpuesta del Jacobiano consiste en premultiplicar (13) a ambos lados por la matriz transpuesta de la matriz Jacobiano, previa verificación del rango de la matriz. Esta premultiplicación construye la matriz cuadrada JTJ en el lado derecho, lo que permite premultiplicar posteriormente a ambos lados por su inversa, [JTJ]-1, y generar la matriz identidad tamaño 5x5 que premultiplica a q , por lo que su expresión queda dada por (16). La ecuación (16) soluciona el problema, pero nuevamente, es necesario el conocimiento de la matriz Jacobiano, J, cuya obtención se presenta a continuación.
C. Matriz Jacobiano
La matriz Jacobiano contiene las derivadas parciales ordinarias de una función escalar, y permite relacionar las diferentes componentes del estado de velocidad y aceleración del efector final con las articulaciones de un manipulador [12]. Para determinar la matriz Jacobiano del Mitsubishi RV-M1 se utilizará la matiz de transformación presentada en [10], reescrita en (17), donde los elementos en el lado derecho ya fueron presentados previamente en (9), (10), (11) y (12), y las compontes ri,j en el lado izquierdo corresponden a la rotación del sistema coordenado de la herramienta respecto al fijo, pasando por cada uno de los sistemas coordenados correspondientes a cada articulación; y las componentes Pi representan la posición del efector final respecto al marco fijo.
La primera fila de la matriz Jacobiano resulta de derivar (10) respecto a cada una de las articulaciones para obtener
Donde
Las ecuaciones (19) a (23) corresponden a las componentes J11, J12, J13, J14 y J15 de la matriz J6x5, respectivamente. De igual forma, se derivan (11) y (12) para determinar las filas 2 y 3 de la matriz Jacobiano.
donde
donde
Las últimas tres filas (inferiores) de la matriz Jacobiano se obtienen de igualar la matriz antisimétrica, ω , del vector de velocidad angular [ωx, ωy, ωz]T, con el producto matricial entre la derivada de primer orden de la matriz de rotación, T F R , y su traspuesta, T F R T , de acuerdo con [2]:
la matriz antisimétrica tiene la estructura
La matriz de rotación T F R se extraerá de (9):
En cuanto a la derivada de la matriz de rotación, se deriva cada término de la matriz con respecto a cada una de las variables articulares qi:
obteniéndose la expresión:
donde
Reemplazando la matriz traspuesta de (37) y la matriz (39) en (35) se obtiene, por ejemplo, para el término ω 11 :
para reducir y obtener lo que se define en (36), que
Un procedimiento similar se emplea para las componentes diagonales y se verifica que ω 22 = ω 33 = 0. Sin embargo, utilizando las componentes fuera de la diagonal principal, es posible obtener las velocidades angulares de la herramienta en el marco fijo, dadas por (51), (52) y (53), respectivamente.
Al observar (14), se distingue que los últimos tres términos están definidos por ωx, ωy y ωz, que son los mismos presentados en (51), (52) y (53), respectivamente, por lo que es posible rearreglar tales ecuaciones para distinguir los coeficientes de los términos φ 1 , θ 2 , θ 3 , θ 4 y θ 5 , y deducir de esta manera los términos J41, J42, J43, J44 y J45, a partir de (51); los términos J51, J52, J53, J54 y J55 a partir de (52), y los términos J61, J62, J63, J64, y J65 de la matriz Jacobiano a partir de (53). De esta manera se han obtenido todos los términos de la matriz Jacobiano del Mitsubishi RV-M1, la cual es presentada en (54). Las componentes Jmn cuyo valor sea cero expresan la no influencia de la articulación Jn en el valor de la componente m del estado de velocidad de la herramienta, X .
Donde
IV. CINEMÁTICA DE ACELERACIÓN DEL ROBOT RV-M1
La cinemática de aceleración representa un importante aspecto en el control de fuerza de manipuladores a lo largo de una trayectoria, y permite determinar el estado de aceleración de la herramienta (compuesto por tres aceleraciones lineales y tres aceleraciones angulares) con las aceleraciones angulares de las juntas actuadas. La Fig. 3b ilustra las aceleraciones angulares de las juntas y el estado de aceleración de la herramienta, X . Similar a la cinemática de posición y velocidad, se consideran los problemas de cinemática de aceleración tanto directo como inverso.
A. Cinemática directa de aceleración
La cinemática directa de aceleración busca conocer el efecto que tiene, en el movimiento de la herramienta, la aceleración de cada una de las articulaciones para cada punto de una trayectoria. El problema se puede plantear como: conocidos los ángulos de posición de las juntas, la posición y la orientación de la herramienta, las velocidades de las juntas, estado de velocidad de la herramienta (velocidades a lo largo de los ejes X, Y y Z y aceleraciones angulares alrededor de los ejes X, Y y Z), halle el estado de aceleración de la herramienta.
La solución al problema es sencilla al derivar (13) con respecto al tiempo, para obtener:
Donde X : estado de aceleración del efector final dado por
donde x : aceleración lineal de la herramienta a lo largo del eje X, y : aceleración lineal de la herramienta a lo largo del eje Y, z : aceleración lineal de la herramienta a lo largo del eje Z, αx: aceleración angular de la herramienta alrededor del eje X, αy: aceleración angular de la herramienta alrededor del eje Y, αz: aceleración angular de la herramienta alrededor del eje Z. El término q es el vector de aceleración de las juntas dado por (75), con αi: aceleración de la junta i-ésima.
El término faltante en (73) es J , definido por la derivada de la matriz Jacobiano. La obtención del nuevo término J , se presenta a continuación.
Cada una de las componentes de la matriz Jacobiano tiene variables articulares, por lo tanto, para obtener su derivada se deriva parcialmente cada término de la matriz con respecto al tiempo, mediante la aplicación de (76)
para obtener los 30 términos presentados en (77) a (93)
Donde
B. Cinemática inversa de aceleración
En la cinemática inversa de aceleración se desea conocer las aceleraciones de las juntas actuadas en función del estado de aceleración de la herramienta. El problema puede plantearse como: conocidos los ángulos de posición del robot, la posición y la orientación de la herramienta, las velocidades de las juntas, la velocidad lineal de la herramienta, las velocidades angulares de la herramienta, la aceleración lineal de la herramienta y las aceleraciones angulares de la herramienta, halle las aceleraciones de las juntas. La solución al problema requiere de aplicar el método de la traspuesta del Jacobiano, esta vez a (73). Primero se reescribe (73) como
luego se premultiplica a ambos lados por JT,
expresión que después de simplificaciones permite despejar el vector q , presentado en (96).
V. VALIDACIÓN DE LA CINEMÁTICA DE VELOCIDAD
Se validó experimentalmente la formulación matemática, comparando los valores reales de velocidad angular en las articulaciones con el comportamiento cinemático de velocidad evaluado mediante el modelo matemático, para una tarea cinemática realizable por el robot Mitsubishi RV-M1. Se creó una interfaz en ambiente GUIDE de Matlab, llamada AMDC RV-M1 [21], siglas de “Aplicativo en Matlab para el Desarrollo de la Cinemática del RV-M1”. La Fig. 4 presenta el algoritmo con los pasos seguidos para su creación, realiza cálculos de cinemática directa o inversa, de velocidad como y aceleración, y grafica los resultados.
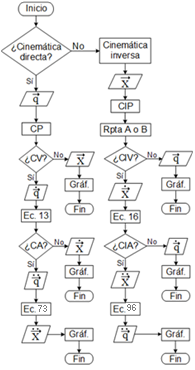
Fig. 4 Algoritmo de la interfaz desarrollada para facilitar los cálculos de la cinemática de velocidad y aceleración.
Para obtener los valores reales de velocidad angular en las articulaciones, durante la tarea cinemática, se utilizó un sistema de adquisición de datos (DAQ por sus siglas en inglés de Data Acquisition System) que permite la medición en tiempo real de las variaciones angulares de las juntas involucradas en el movimiento [17]. El DAQ cuenta con un giroscopio L3GD20 [22] que mide velocidades angulares alrededor de los tres ejes. Su rango de medición es variable: ±250 °/s (escogida), ±500 °/s o ±2000 °/s. Este se comunica y envía los datos leídos por medio de una antena Bluetooth Modem BlueSMiRF Gold [23], que trabaja como una línea de comunicación serial (TX/RX), utilizando el microcontrolador Arduino Uno como plataforma de procesamiento. El sensor y la antena Bluetooth van montados sobre una placa shield para conexión con el microcontrolador, Fig. 5.
A. Selección y programación de la trayectoria
Se toma como trayectoria una trayectoria lineal descendente desde el punto P1=(500, 0, 450)mm a P2=(500, 0, 200)mm con referencia en el marco xF-yF-zF, Fig. 2d, con orientación de la herramienta constante, asemejando la aplicación de un cordón lineal de soldadura vertical. Se establece la velocidad de la herramienta en “SP 3”, equivalente a una velocidad lineal media en la herramienta de 35.89 mm/s. Se establece comunicación serial con el controlador del robot con Matlab, y se ordena al robot completar la trayectoria mediante los comandos “MP”, “HE”, “SP” y “MS” extraídos del manual de usuario [16].
B. Medición de las velocidades angulares
El DAQ construido se ubica sobre la cara superior de los eslabones, como se observa en la Fig. 6. La trayectoria se realiza en el plano XZ y la orientación de la herramienta se mantiene constante, por lo cual sólo es necesario medir las velocidades angulares en los eslabones 2, 3 y 4. El envío de datos del DAQ a teléfono Android se hizo con la aplicación Bluetooth Serial Controller [24].
VI. RESULTADOS
Se hicieron 10 mediciones para cada articulación, en cada una de ellas el DAQ entrega 70 datos entre el inicio y final de la trayectoria; se asume que cada dato Di (1 ≤ i ≤ 70) de cada medición corresponde a la medición de velocidad angular en el mismo punto, de modo que se tendrán 70 puntos de muestreo entre los puntos extremos P1 y P2, incluidos.
Normalmente, cuando se tiene una cantidad n de mediciones que corresponden a un mismo valor real de la variable medida, se encuentran valores que se desvían aparentemente de la tendencia del conjunto, conocidos como Outliers o valores extraños, que pueden resultar de la falta de control sobre el error sistemático en el procedimiento de medición [25]. En este caso, este error se origina por la estrategia de control del robot y la presencia de vibraciones en el robot. En [25] se describe el criterio de Chauvenet para la detección de Outliers en un conjunto de n datos, con probabilidad de ocurrencia menor a 1/2n mediante
donde P(Z0): valor de probabilidad para una función de error normal y Z0 está dado por la expresión
con xi: dato sospechoso, x : promedio del conjunto de datos y Sx: desviación estándar de la muestra. Para n=10 se consideran como valores extraño aquellos con probabilidad de ocurrencia menor a 0.05% a partir de (97).
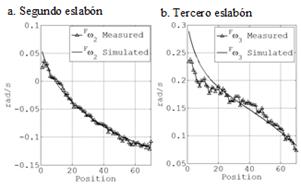
La Fig. 7 muestra las lecturas del DAQ durante la trayectoria con la etiqueta “Measured”, para las velocidades angulares en el marco fijo Fω2 y Fω3, y las compara con las velocidades obtenidas mediante programación de cinemática inversa de velocidad, distinguidas con la etiqueta “Simulated”.
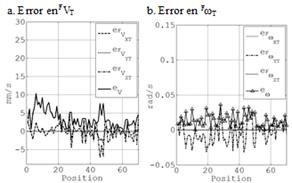
La Fig. 8a presenta el valor de la velocidad angular del cuarto eslabón en el marco fijo, Fω4. La velocidad teórica o calculada es etiquetada con “Simulated” en esa figura, y comparada contra las mediciones reales arrojadas por el DAQ con la etiqueta “Measured”. La Fig. 8b presenta los errores absolutos de las velocidades angulares de los elementos 2, 3 y 4 en el marco fijo, denotados como Fω2, Fω3 y Fω4, respectivamente, que fueron obtenidos al comparar los valores teórico, FωT, con el leído por el dispositivo, FωDAQ, mediante
Debido a la disposición y eje de rotación del primer eslabón la velocidad Fω2, en la Fig. 7a, es absoluta (corresponde totalmente a la rotación de la segunda articulación). Para el caso de Fω3 correspondiente a la velocidad angular del tercer eslabón en el fijo no se ve afectada por las velocidades de los elementos cuarto y quinto, quedando expresado su estado de velocidad como
con F X 3 definido por
y F x 3, F y 3 y F z 3 son las velocidades lineales de la tercera articulación a lo largo de los ejes xF, yF y zF, respectivamente; Fωx3, Fωy3 y Fωz3 son las velocidades angulares alrededor de los ejes xF, yF y zF, respectivamente; y FJ3 es la matriz Jacobiano del tercer eslabón en el marco fijo, la cual es hallada a partir de la matriz de transformación del tercer elemento en el marco fijo construida mediante (102). Finalmente, la velocidad Fω3 se halla a partir de las componentes en (101) mediante (103). Los pasos de las ecuaciones (100) a (103) se repiten para el estado de velocidad del cuarto eslabón en el fijo F X 4 y obtener Fω4. Para el estado de velocidad de la herramienta, FVT, y el vector q , del que se extraen cada una de las velocidad angulares ωi, se cuenta con (13) a través de la interfaz en Matlab mencionada.
La velocidad y aceleración angular del cuarto eslabón en el fijo, Fω4 y Fα4, puesto que no varía la orientación de la herramienta en la tarea. Aun cuando solo se valida experimentalmente la velocidad angular, una estimación de la validez del modelo cinemático planteado resulta al comparar las curvas de velocidad y aceleración angular teóricas para la articulaciones 2 y 3 en el marco fijo, con las calculadas en base a las mediciones realizadas. Para ello, se deriva la el Jacobiano, FJ3, en (100), obteniéndose F J 3, término que permite expresar (73) como (104) y obtener la expresión (105).
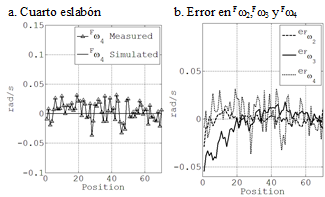
Fig. 8 Velocidad angular del cuarto eslabón ω4, en el marco fijo, medida y simulada y error en las velocidades angulares.
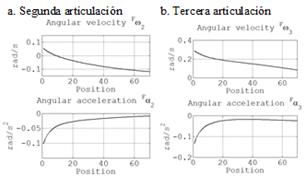
El comportamiento de las velocidades y aceleraciones angulares ω2, Fωy3, α2 y Fαy3 obtenido teóricamente se muestra en las Fig. 9a y 9b. Siendo la aceleración angular la razón de cambio de la velocidad angular, el valor de aceleración angular en cada posición de la trayectoria en la Fig. 9 estará definido por el cociente entre Δω y el tiempo trascurrido entre cada posición (para la tarea cinemática realizada es de aproximadamente 0.1 seg).
VII. DISCUSIÓN DE RESULTADOS
Se consideran los aspectos que afectan directamente la precisión de los resultados.
Limitaciones de control (movimiento Punto A Punto-PTP): Las pruebas se realizaron mientras el manipulador describía un movimiento vertical descendente, con una velocidad de 35.89 mm/s. Idealmente el movimiento es en línea recta, pero se aproximó la tarea cinemática utilizando el comando MS (Move straight) que genera n (1<n<99) puntos entre P1 y P2. El movimiento entre los puntos generados se realiza mediante interpolación articular, véase las curvas de aproximación en la Fig. 10. Del valor de n depende la proximidad entre el movimiento del robot y el deseado y la estabilidad de la estructura física.
Vibración de la estructura física del manipulador: un mayor número de puntos entre P1 y P2 acorta la distancia entre ellos, y hace más inestable es la estructura del robot, presentándose vibraciones de diferente magnitud a lo largo de la trayectoria que afectan directamente la medición de la velocidad. Las vibraciones de baja amplitud son filtradas por el DAQ construido, sin embargo, una gran parte de vibraciones a lo largo de la trayectoria de mayor amplitud generan rizado y saltos en la curva correspondiente a los datos obtenidos.
Precisión del dispositivo de medición: del procedimiento de calibración se estableció un intervalo de incertidumbre para la medición de ±0.65°/s (0.011 rad/s). Las Fig. 11a y 11b muestran la diferencia que existe al simular la cinemática directa de velocidad lineal del robot con la interfaz AMDC RV-M1 usando como datos de entrada los valores obtenidos al simular la cinemática inversa de velocidad, contra los valores obtenidos de la medición utilizando el DAQ.
A pesar de que únicamente debería existir velocidad en el eje Z, la presencia de velocidad en el eje X es atribuida a la aproximación tipo arco de punto a punto inherente al controlador suministrado por el fabricante y de hardware inaccesible. Lo anterior modifica, inclusive, la velocidad en el eje Z, así como la pequeña variación en la inclinación de la herramienta mostrada en la Fig. 11b.
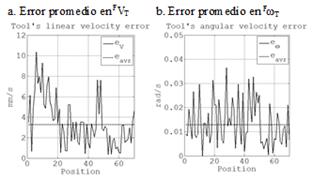
El error absoluto en la velocidad lineal de la herramienta a lo largo de la tarea cinemática se observa en la Fig. 12a. El mayor error se tiene al inicio de la tarea, con excepción de un pico de error atribuible a un pico de vibración del sistema en la tercera y cuarta articulación, puesto que experimentan las mayores velocidades de la trayectoria, al ser exigido el controlador puesto que se requiere mayor cantidad de pulsos de los encoders que gobiernan a los servomotores. En promedio se tiene un error de 3.28 mm/s para la velocidad lineal de la herramienta. La Fig. 12b muestra el error absoluto las desviaciones de velocidad angular en la herramienta. Se tiene entonces un promedio de error absoluto de velocidad angular de la herramienta a lo largo de la trayectoria menor a 0.015 rad/s, valor aceptable dada las condiciones del procedimiento de validación, las limitaciones en el acceso al control del robot y al envejecimiento del mismo, dada la antigüedad del hardware.
VIII. CONCLUSIONES
A partir de la matriz de transformación de posición de la herramienta del robot Mitsubishi RV-M1 se deducen las expresiones que permiten determinar la matriz Jacobiano de este manipulador. El conocimiento de este arreglo permitió el planteamiento explícito matricial de las soluciones de la cinemática de velocidad y de aceleración, directa e inversa en cada caso. A partir de estas ecuaciones, se programó una interfaz gráfica de usuario que resume la ejecución de seis funciones de cálculo: posición, velocidad y aceleración, tanto análisis directo como inverso. La metodología de cálculo propuesta en la interfaz se utilizó para simular una trayectoria lineal vertical, semejante a un cordón vertical de soldadura de 250 mm de longitud. La simulación en la interfaz permitió verificar que el cordón estaba dentro del espacio de trabajo del robot, y obtener los valores de ángulos, velocidad y aceleración de cada junta del robot. Se implementó la tarea cinemática en el robot con la asistencia de un DAQ básico, construido para medir los valores de velocidad angular de cada junta. La confrontación de los valores calculados en la interfaz y los arrojados por el DAQ permitieron establecer una gran concordancia entre el modelo teórico desarrollado y el desempeño real, con errores promedio en la velocidad lineal de la herramienta de 3.28 mm/s, y de 0.015 rad/s para la velocidad angular, valores aceptables y razonablemente atribuibles a la naturaleza del movimiento de aproximación de punto a punto inherente al controlador original del robot. Se considera este trabajo como un aporte significativo a la robótica de manipuladores seriales, por cuanto no existe literatura que reporte un trabajo similar para el robot en estudio.