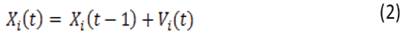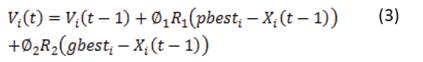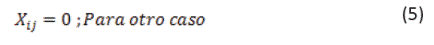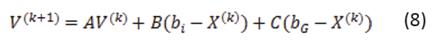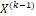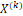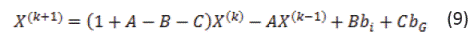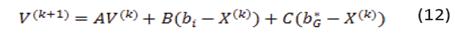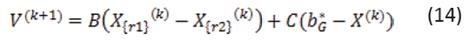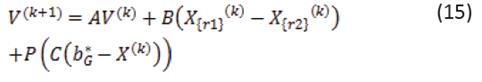I. INTRODUCCIÓN
La reconfiguración de las redes de distribución es uno de los mecanismos más importantes en la operación de los sistemas eléctricos de potencia. El problema de reconfigurar una red de distribución es encontrar una estructura de operación radial (típica en estos sistemas y la más utilizada) que minimice las pérdidas de potencia del sistema. Además, se deben satisfacer las restricciones de operación, tales como niveles de tensión apropiados para la operación del sistema, limitantes de la topología de la red, entre otros. La principal motivación para realizar el estudio de este tipo de redes, es que las pérdidas de potencia en sistemas de distribución son elevadas. Por ejemplo, en Colombia, según datos de la UPME (Unidad de Planeación Minero Energética) las pérdidas de potencia son cercanas al 16 % del total de la potencia generada. Dichas pérdidas son causadas en su mayoría por efecto joule en los conductores, lo cual conlleva al aumento en los costos de operación, estos a su vez, asumidos por el usuario.
Teniendo en cuenta lo anterior, se realiza el análisis de posibles soluciones mediante el uso de métodos heurísticos que se caracterizan por encontrar soluciones óptimas con tiempos cortos de cómputo [1]. Los métodos a utilizar son DEEPSO (Differential Evolutionary Particle Swarm Optimization) y BPSO (Binary Particle Swarm Optimization) ya que estos han sido utilizados en diferentes problemas de optimización de sistemas de potencia [1-6]. Cada una de estas herramientas permite realizar un análisis eficiente del comportamiento de un sistema determinado. Así pues, se implementó cada algoritmo a las redes de prueba de 33 y 69 nodos. De esta manera, se evaluaron en cada caso los niveles de tensión en cada nodo, las pérdidas de potencia, la eficiencia y los tiempos de ejecución.
Varios métodos heurísticos han sido utilizados para abordar este tipo de problemas [7-8]. Trabajo previo como el de A. González en 2007 [2] presenta una serie de algoritmos heurísticos y evolutivos que se enfocan en reconectar circuitos primarios en redes de distribución, de tal manera que se puedan encontrar redes con topologías en las que la confiabilidad sea el factor primordial a la hora de prestar el servicio de energía eléctrica. En este mismo trabajo se plantea el uso de dichos algoritmos para determinar la forma más rápida de restaurar el servicio de energía eléctrica en sistemas de distribución. Así pues, se realiza la reconfiguración de alimentadores en el sistema, de tal forma que se tengan en cuenta las restricciones de topología existentes y aumente la confiabilidad en la prestación del servicio.
Otro trabajo relacionado a este tema es el presentado por J. González e I. Lisanen en 2012 [3], en el cual se realiza un modelamiento matemático para el intercambio de ramas de sistemas de distribución enfocados en reconfigurar un sistema para que opere de forma radial y permita así reducir las pérdidas de potencia del sistema, claro está, satisfaciendo las restricciones de operación.
Otro ejemplo de aplicación de algoritmos heurísticos como el BPSO es el trabajo hecho por K. Kiran y N. Ventaka en 1992 [4], donde se propone un algoritmo de optimización por enjambre de partículas para la reconfiguración multiobjetivo de sistemas de distribución. Este algoritmo tiene como fin minimizar las pérdidas de potencia, controlar las caídas de tensión para mantener operando el sistema dentro de los límites térmicos de los circuitos alimentadores con respecto a sus capacidades de carga. El algoritmo asocia las partículas de un enjambre al comportamiento nodal y ramal del sistema para determinar qué líneas deben conectarse o desconectarse, analizando el efecto de dichos cambios desde el punto de vista de las pérdidas, los valores de tensión y la radialidad del sistema.
De esta manera, el presente artículo presenta en la sección II la formulación y la metodología del problema a solucionar correspondiente a la reconfiguración de sistemas de distribución para minimizar pérdidas. Como metodología se describen los dos métodos (BPSO y DEEPSO) de optimización heurística elegidos para solucionar el problema. En la sección III se presentan los resultados de simulación obtenidos y en la sección IV las conclusiones.
II. FORMULACIÓN Y METODOLOGÍA
A. Función Objetivo y Restricciones
1) Función Objetivo: es la función que se busca optimizar, para este caso particular son las pérdidas de potencia debido a los parámetros físicos de las líneas y el efecto joule (disipación de calor), se pierde potencia en la operación de un sistema eléctrico. El objetivo es minimizar dichas perdidas.
2) Topología: se debe considerar la disposición de las conexiones entre los nodos a evaluar, cómo se organizan las ramas y cómo se dan los flujos de potencia.
3) Radialidad: esta característica puede ser evaluada por medio de la siguiente condición:
donde:
N r = Número de ramas conectadas del sistema
N n = Número total de nodos conectados en el sistema.
4) Niveles de Tensión: la condición idónea para el valor´ de tensión debe ser de 1 p.u (por unidad) o en su defecto lo más cercano posible, con el fin de evitar diferencias de potencial muy altas que generen mayores pérdidas.
B. Método de Análisis y Aplicación
Para realizar el análisis de reconfiguración se aplican los algoritmos heurísticos DEEPSO y BPSO, a dos casos particulares de redes de distribución de: 33 y 69 nodos [5]. El proceso consiste en realizar un análisis de las condiciones de operación del sistema, además de las características físicas de conexión y parámetros de algunos equipos como generadores.
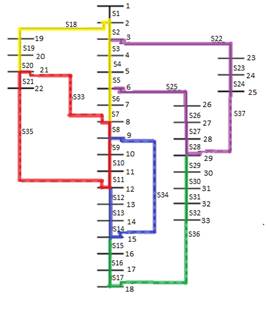
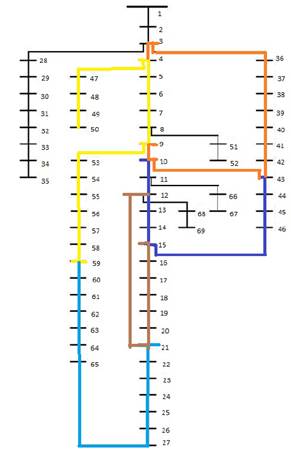
Previo a la aplicación de algún método se deben analizar qué variables de decisión pueden ser establecidas y cómo serán utilizadas. En ambos métodos se emplea como variable de decisión el estado de los interruptores (abierto o cerrado), que interconectan las ramas del sistema. Los interruptores se asocian en grupos de tal forma que se encuentren en cascada, es decir, su disposición física debe ser continua. Se establecen 5 grupos de máximo 9 interruptores (en la red de 33 nodos) y máximo 16 (en la red de 69 nodos) como se muestra en las Fig. 1 y Fig. 2, respectivamente.
En operación real, estos grupos representan la zona donde trabajan las cuadrillas de la empresa encargada de la red de distribución. Los algoritmos realizan un flujo de potencia (Método numérico Newton Raphson desacoplado), para determinar características de operación como pérdidas de potencia y niveles de tensión. Se evalúa el comportamiento de diferentes configuraciones, luego mediante las variables de decisión se busca definir los estados de un grupo específico de interruptores, que representen la configuración óptima para minimizar las pérdidas de potencia.
C. BPSO
El algoritmo de reconfiguración basado en BPSO se utiliza para encontrar la configuración óptima de los interruptores en las redes. Este método se ha usado para optimizar funciones continuas que no son lineales [6-10]. El BPSO realiza el intercambio de información entre los individuos o las llamadas partículas de la población que conforman el enjambre, el cual contiene la información de las características de las funciones y del sistema a analizar. Cada partícula ajusta su propia posición basada en su experiencia previa y busca ubicarse en la mejor posición del enjambre. El movimiento de partículas hacia la solución óptima es guiado por el conocimiento individual y colectivo de las mismas. La ubicación de la partícula en cualquier momento se determina por su velocidad y la posición previa, como se muestra a continuación en (2):
En esta expresión: 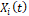 y
y 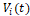 son vectores de posición asociados a la i-ésima partícula en el instante
son vectores de posición asociados a la i-ésima partícula en el instante 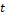 y
y 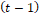 . Adicionalmente
. Adicionalmente 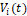 es el vector de velocidad correspondiente a la partícula. Dicho vector de velocidad se actualiza a partir de la información adquirida individualmente y en conjunto. La regla de actualización de velocidad para un algoritmo basado en BPSO es:
es el vector de velocidad correspondiente a la partícula. Dicho vector de velocidad se actualiza a partir de la información adquirida individualmente y en conjunto. La regla de actualización de velocidad para un algoritmo basado en BPSO es:
donde:
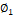 : aceleración constante individual.
: aceleración constante individual.
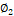 : aceleración constante social.
: aceleración constante social.
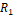 y
y 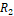 : valores aleatorios en el rango [0, 1];
: valores aleatorios en el rango [0, 1];
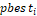 : vector de posición ideal hallado por la i-ésima partícula
: vector de posición ideal hallado por la i-ésima partícula
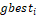 : los vectores de posición ideales hallados por todas las partículas.
: los vectores de posición ideales hallados por todas las partículas.
En el algoritmo BPSO, cada uno de los elementos del vector de posición sólo puede adoptar valores binarios (0 o 1). En cada etapa de iteración, el vector de posición 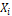 se actualiza de acuerdo con la siguiente regla:
se actualiza de acuerdo con la siguiente regla:
donde:
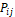 : número aleatorio en el rango [0,1].
: número aleatorio en el rango [0,1].
En este caso, la función sigmoide se usa para describir el comportamiento evolutivo del sistema que tiene una aceleración intermedia en el proceso de aprendizaje. Dicha función es de la forma:
En el algoritmo basado en BPSO, la población de partículas inicia con valores al azar y se evalúa para calcular la función $Fitness$ (es la función de evaluación o función objetivo, es decir, es lo que se quiere llegar a optimizar) en conjunto para luego buscar la mejor partícula, lo cual significa, la que tenga las mejores características hasta el momento. Por otro lado, se debe hallar el mejor global, dicho en otras palabras, la mejor partícula en el enjambre entero.
El mejor individuo entre la población de partículas, con sus dimensiones y el valor de la aptitud es asignado al mejor global. A continuación, se inicia un ciclo que tiende a converger a una solución cercana a la óptima. En el ciclo, las mejores partículas y los mejores globales determinan cómo actualizar la velocidad. De esta manera, la posición actual de cada partícula se cambia con la velocidad de ese instante. La evaluación es realizada nuevamente de tal manera que se pueda calcular la aptitud de cada partícula perteneciente al enjambre. Este ciclo es detenido según el número de iteraciones que se definan.
D. DEEPSO
El método DEEPSO es el resultado de combinar varios métodos de optimización, en los cuales se busca aprovechar las características principales de cada uno en la búsqueda de obtener el valor óptimo mediante una solución correcta a nivel global [6]. Sin embargo, cada método presenta una serie de dificultades en relación al análisis de un problema específico, el procesamiento y la precisión de los resultados obtenidos. Es por ello, que, mediante adecuadas combinaciones de métodos, se deriva un método más robusto y general.
El algoritmo de optimización DEEPSO se origina a partir del método EPSO (Evolutionary Particle Swarm Optimization). Según el estudio y la recopilación de datos hecha en [6] del método DEEPSO se describe que la versión básica del algoritmo se presentó en el año 2002. En [9]; se muestra que se introdujo como una forma en la que "al unir el poder exploratorio de PSO (Particle Swarm Optimization) con el poder de auto-adaptación de los Algoritmos Evolutivos (EA) se tiene como resultado lo mejor de dos mundos".
Para poder entender dicho método primero se hará una breve explicación de cada uno de los métodos utilizados en su formación.
1) PSO Como un proceso de recombinación
La Optimización de enjambre de partículas (PSO) explicada en [10] se basa en una regla de movimiento que genera nuevos individuos en el espacio, a partir de un conjunto de alternativas previamente conocidas. Desde dicha regla de movimiento básica se produce un nuevo vector individual de soluciones X para la iteración (k + 1):
Donde V es llamada la velocidad de la partícula y está definida como:
Donde 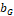 es el mejor punto hasta ahora encontrado por el enjambre y
es el mejor punto hasta ahora encontrado por el enjambre y 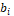 es el mejor antepasado directo de la partícula, con
es el mejor antepasado directo de la partícula, con 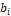 , i = 1, ...N. Partículas} = Pb formando el conjunto de los mejores ancestros en el comportamiento histórico de cada partícula.
, i = 1, ...N. Partículas} = Pb formando el conjunto de los mejores ancestros en el comportamiento histórico de cada partícula.
Cada parámetro (A, B, C) es una matriz diagonal con una incidencia definida al comienzo del proceso. En una formulación clásica, el parámetro A se ve afectado por un valor decreciente con el tiempo, es decir, cambia en cada iteración, mientras que los parámetros iniciales B y C se multiplican con éxito mediante números aleatorios como es explicado en [10] tomados de una distribución uniforme en el intervalo de [0,1]. A partir de las ecuaciones (7) y (8) se infiere que una partícula nueva 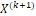 , se origina como una combinación de los siguientes elementos:
, se origina como una combinación de los siguientes elementos:
Se puede dar un aspecto diferente a la definición de la ecuación (8):
Esta expresión es la suma de los parámetros que multiplican los cuatro contribuyentes para generar la descendencia. Por lo tanto, se está considerando una población que incluye no sólo las partículas activas, sino también las que son antepasados inmediatos y el conjunto de los mejores antepasados. De esta manera, se evalúa el camino recorrido por la partícula en los recientes cambios.
2) EPSO: una recombinación adaptativa evolutiva.
El propósito del algoritmo EPSO fue proporcionar la habilidad de adaptación al parámetro de recombinación [9]. Para realizar esto, los elementos en la ecuación (8) están sujetos a mutación y selección, de tal forma que se pueda obtener una mejor tasa de progreso. Si se tiene una población formada por un conjunto de partículas, la estructura general de EPSO resulta en:
Replicación: cada partícula clonada r veces (normalmente r = 1).
Mutación: en cada partícula r los parámetros A, B, C son mutados.
Reproducción: cada partícula r+1 (original y clon) produce un descendiente por medio de la recombinación, acorde a la regla de movimiento de partículas en (8) y (9).
Evaluación: a la población se le evalúa su aptitud.
Selección: mediante un proceso de selección como torneo estocástico, se forma una nueva generación con el mejor descendiente de cada antepasado, esto es posible ya que cada individuo perteneciente a una generación anterior tiene un descendiente.
La mutación de cada uno de los parámetros A, B, C (representada por la letra W). En (9) es restringida por valores aleatorios multiplicativos tal que 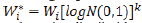
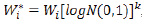 o por valores aleatorios distribuidos gaussianos aditivos tales como
o por valores aleatorios distribuidos gaussianos aditivos tales como 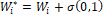 . El operador de aprendizaje (
. El operador de aprendizaje (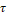 o
o  ) tiene que ser fijado externamente. El parámetro de recombinación está definido por cada elemento A, B y C, la estructura resulta en un operador de recombinación adaptativa.
) tiene que ser fijado externamente. El parámetro de recombinación está definido por cada elemento A, B y C, la estructura resulta en un operador de recombinación adaptativa.
El método EPSO se hizo más eficiente con la introducción de dos adiciones. En las primeras versiones, se mostró que el ruido que afectaba la ubicación exacta de 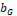 era beneficiosa, por lo que se introdujo un cuarto parámetro o peso en forma de una matriz diagonal
era beneficiosa, por lo que se introdujo un cuarto parámetro o peso en forma de una matriz diagonal 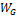 , tal que:
, tal que:
Este peso también está sujeto a mutaciones del tipo mencionado anteriormente, por lo que también entra en el modelo autoadaptable. Por último, en la versión más actualizada y eficiente, se incluyó un peso de comunicación P, que crea una topología en comunicación (Stochastic Star) para el enjambre de partículas. La regla para la recombinación (o movimiento) de EPSO es:
En la que P es una matriz diagonal que afecta a todas las dimensiones de un individuo, que contiene variables binarias de valor 1 con probabilidad p y valor 0 con probabilidad (1-p). La probabilidad de comunicación de valor de $p$ controla el paso de información dentro del enjambre y es 1 en formulaciones clásicas (como la Stochastic Star). Este esquema estocástico oscila conceptualmente entre la disposición estelar y una versión llamada modelo cognitivo [10], donde no existe comunicación. La estrella estocástica hace que en algunos elementos del mejor global sean "notados" por una partícula y entretanto otros sean ignorados, de tal forma que la fabricación de una nueva partícula es afectada en distintas maneras en sus diferentes dimensiones. Esto facilita el desacoplamiento de la evolución en cada una de las dimensiones.
3) DE
La idea original detrás de DE (Diferential Evolution), es que dada una población (enjambre) de individuos (partículas, vectores), se genera una nueva solución de un individuo existente añadiendo alguna fracción de la diferencia entre otros dos puntos de posición 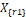 y
y 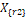 tomados de la población o enjambre [11]. Es decir, en cada nueva población originada, se establece una recombinación adicional que garantice una mayor diversidad y un procedimiento de selección que fabrique la siguiente generación. Esta selección es elitista y basada en uno-a-uno, esto significa que cada padre compite por la supervivencia directamente con su único hijo y lo mejor es retenido. Hay diversas modificaciones para este esquema. Uno particular es el que es llamado DE2 [11], en el cual la producción de un nuevo individuo puede ser establecida como:
tomados de la población o enjambre [11]. Es decir, en cada nueva población originada, se establece una recombinación adicional que garantice una mayor diversidad y un procedimiento de selección que fabrique la siguiente generación. Esta selección es elitista y basada en uno-a-uno, esto significa que cada padre compite por la supervivencia directamente con su único hijo y lo mejor es retenido. Hay diversas modificaciones para este esquema. Uno particular es el que es llamado DE2 [11], en el cual la producción de un nuevo individuo puede ser establecida como:
Se adopta aquí una forma distinta con el fin de observar las similitudes con (7) y (8), es decir, entre DE y PSO en el proceso de generación de nuevos individuos a partir de las ecuaciones de nuevas posiciones y velocidades. La versión canónica de DE hace C = 0; y la versión canónica DE hace B = C. Dejando de lado la recombinación, el DE continua con una selección de padres (escogiendo la siguiente generación tanto de las poblaciones de progenitores como de descendientes) de un tipo especial en la que cada padre compite solo con su descendencia mientras que PSO adopta de alguna manera una selección trivial de superviviente (se elige entre los descendientes solamente). EPSO dispone también de un procedimiento especial de selección de supervivientes, en el que la competencia se establece únicamente entre los descendientes directos de cada partícula.
Con el estudio de las características de cada método se evidenció que el método DE, realizaba un muestreo de un macro-gradiente local en la función objetivo reuniendo dos individuos aleatorios de la población [6]. Este mismo tipo de muestreo es realizado por la ecuación de movimiento PSO, pero recolectando la posición actual y la mejor hasta el momento, de dicha partícula. Por lo tanto, es posible pensar que el esquema DE no funcionaría correctamente cuando se inserta en la ecuación PSO como se hizo con los algoritmos evolutivos [11]. Así mismo, el método DE se basa en valores fijos de parámetros B en el intervalo (0,1). El algoritmo DEEPSO es similar en su secuencia al EPSO. Para visualizar la introducción de la evolución diferencial, se expresa la siguiente ecuación general de la regla de movimiento:
Donde 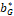 está dado en la ecuación (10). En la expresión (15),
está dado en la ecuación (10). En la expresión (15), 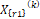 y
y 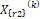 son cualquier par de partículas diferentes, que pertenecen en principio al grupo de las partículas de la generación actual.
son cualquier par de partículas diferentes, que pertenecen en principio al grupo de las partículas de la generación actual.
III. RESULTADOS DE SIMULACIÓN.
Mediante el uso de la herramienta MATLAB se aplicaron los métodos BPSO y DEEPSO para comparar las características de dichos métodos. Los casos de estudio a los cuales se les realizó la reconfiguración fueron dos redes de distribución radial, uno de 33 nodos (Fig.1) y otro de 69 nodos (Fig.2). A ambos sistemas se les aplicaron los algoritmos en las mismas condiciones de operación y uso de recursos computacionales provistos por el computador (Asus XC4055 Intel Core i7 - RAM: 8GB - 2,5 GHz).
A. Aplicación de BPSO
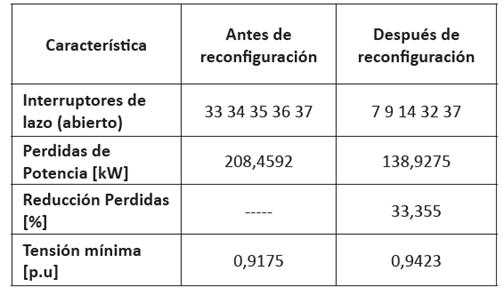
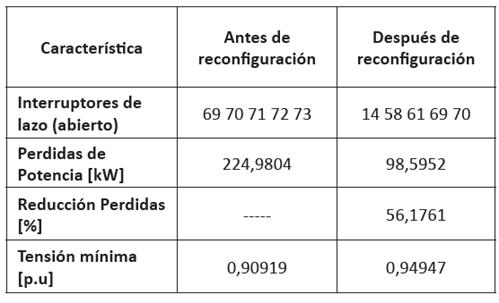
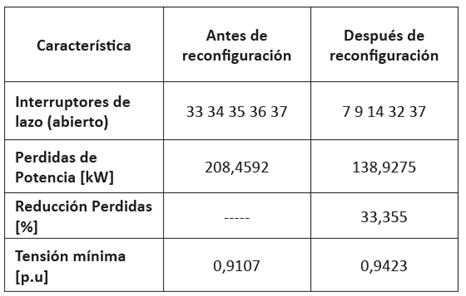
Al utilizar el paquete MATPOWER - Power System Simulation Package [13] Versión 6.0b1 se aplicó el algoritmo de reconfiguración mediante el método BPSO a los sistemas de distribución de 33 y 69 nodos hasta obtener los resultados que se muestran en las tablas I y II.
El tiempo de procesamiento del algoritmo BPSO para el sistema de distribución de 69 nodos fue de 13,42 segundos.
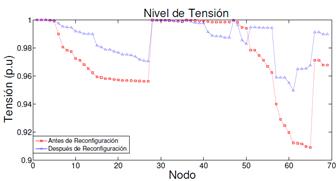
Además de las características de reconfiguración y reducción de pérdidas, el software ofrece la posibilidad de visualizar las tensiones de los nodos del sistema (Fig. 3 y Fig. 4). En las gráficas se muestra cómo cambia el nivel de tensión (eje de ordenadas) en cada nodo (eje de abscisas).

Fig. 3 Comportamiento niveles de tensión en cada nodo del sistema de distribución de 33 nodos: Método BPSO.
B. Aplicación de DEEPSO
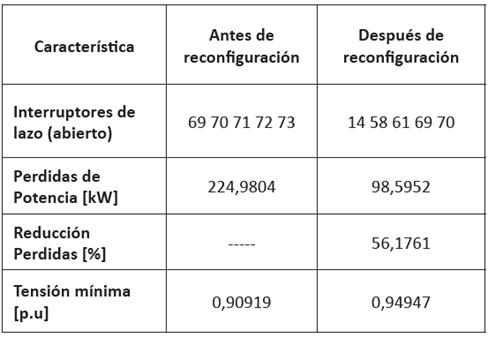
Al utilizar el paquete MATPOWER - Power System Simulation Package [14] Versión 4.1 se aplicó el algoritmo de reconfiguración mediante el método DEEPSO hasta obtener los resultados mostrados en las Tablas III y IV.
El tiempo de procesamiento del algoritmo DEEPSO para el sistema de distribución de 33 nodos fue de 9,45 segundos.
El tiempo de procesamiento del algoritmo DEEPSO para el sistema de distribución de 69 nodos fue de 20,02 segundos.
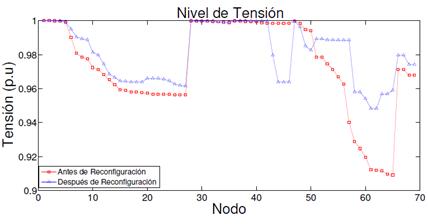
En este caso, en las Fig. 5 y Fig. 6 se muestra el cambio en los niveles de tensión (eje de ordenadas) de cada nodo (eje de abscisas) debido a la reconfiguración.
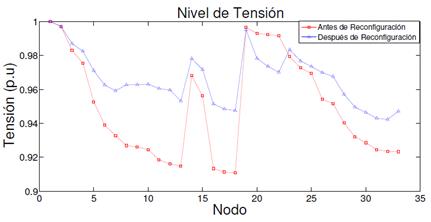
Fig. 5 Comportamiento niveles de tensión en cada nodo del sistema de distribución de 33 nodos: Método DEEPSO.
IV. CONCLUSIONES
Con la implementación de los algoritmos BPSO y DEEPSO en la reconfiguración de sistemas de distribución, se logró reducir las pérdidas de potencia en cada sistema simulado (33% en la red de 33 nodos y 56% en la red de 69 nodos). Se observó que con los dos métodos se obtienen las mismas soluciones en la forma óptima de configurar el sistema y en la reducción de pérdidas.
Teniendo en cuenta que los dos métodos llegan a la misma solución, se infiere que ambos son igual de precisos. Debido a su estructura, DEEPSO es una combinación que aprovecha varios métodos de solución. Por otro lado, BPSO realiza el análisis exploratorio con el uso de una función sigmoidal que describe, el comportamiento evolutivo del sistema simulando la aceleración intermedia de aprendizaje en la búsqueda del resultado óptimo.
El comportamiento de los niveles de tensión observado en las figuras 3, 4, 5 y 6, describe cómo influye la reconfiguración en el sistema. Tal como se esperaba, la nueva disposición de conexión de las líneas dio como resultado mejores niveles de tensión (más cercanos al valor de 1,0 p.u.) en la mayoría de los nodos que conforman la red.
En relación con la eficiencia, se observó que el uso del algoritmo DEEPSO presentó un tiempo de ejecución mayor que el BPSO. Esto se determinó al realizar la optimización heurística en cada sistema en cinco ocasiones. Así pues, al promediar los tiempos de ejecución en las mismas condiciones de procesamiento, se obtuvieron valores de referencia que permitieron comparar la agilidad con la que cada método encuentra la solución de reconfiguración.