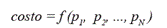I. INTRODUCCIÓN
El servicio del transporte público es una de las principales inquietudes de las autoridades gubernamentales por la necesidad de disminuir los costos y mejorar el servicio. La expansión urbana es una de las razones por la que es preciso reconsiderar los recorridos de las líneas de trasporte. Cuando se inaugura un nuevo barrio o cuando una región tiene un crecimiento demográfico considerable, surge el requerimiento de sus habitantes para que el autobús pase con frecuencia cerca de sus domicilios. Un servicio de transporte eficiente es uno de los elementos principales para conseguir ciudades inteligentes y sostenibles [1].
Esta problemática puede ser representada mediante el problema de localización y ruteo (LRP) general, el cual combina tareas básicas de logística, integrando dos niveles de decisión: localización de los depósitos y ruteo vehicular. En los últimos años ha crecido la cantidad de artículos sobre este tema [2] con distintas aplicaciones y variados enfoques [3]. El estudio de Nagy y Salhi [4] describe técnicas de solución y aplicaciones para este tipo de dificultades, pues está demostrado que este es un problema NP-Completo [5], ya que abarca dos problemas NP-Completos: la ubicación de las instalaciones y la asignación de rutas para los vehículos [6]. En este contexto es recomendable la aplicación de técnicas aproximadas como las metaheurísticas, sobre todo en problemas de grandes dimensiones [7].
Para desarrollar los planteamientos anteriores, el trabajo se organiza de la siguiente manera: la Sección II describe el enfoque hiperheurístico. El caso de estudio abordado es presentado en la Sección III. En la Sección IV se presentan los resultados computacionales. Finalmente, en la Sección V se establecen las conclusiones y los trabajos futuros.
II. ENFOQUE HIPERHEURÍSTICO
Las heurísticas y especialmente las metaheurísticas, demostraron ser capaces de obtener excelentes resultados en problemas de optimización combinatorios complejos, sin tener que adaptarse profundamente a cada problema [8]. Sin embargo, no es posible asegurar que una técnica funcione de manera satisfactoria en múltiples instancias [9]. Esta es la principal razón por la que las hiperheurísticas surgen como nuevas estrategias para resolver esta clase de problemas.
Una hiperheurística es un método de búsqueda general aplicable a múltiples instancias de un problema e incluso, puede utilizarse para resolver problemas distintos. Esta metodología puede pensarse como una heurística para elegir heurísticas [10].
En Burke et al. [11] se define hiperheurística como un método de búsqueda o mecanismo de aprendizaje para seleccionar o generar heurísticas que resuelvan problemas de búsqueda computacionales. Este es un enfoque general, simple y fácil de implementar [12]. Una revisión detallada sobre hiperheurísticas se puede encontrar en [13].
Las hiperheurísticas tienen como objetivo principal el aporte de soluciones generalizadas a los problemas, en lugar de apuntar a los mejores resultados [12]. Entonces, lo que se persigue es incrementar la generalidad de los métodos [10]. La manera en que una hiperheurística guía la búsqueda de una solución consiste en emplear indicadores de desempeño que están relacionados con el funcionamiento de las heurísticas de bajo nivel.
En este trabajo presentamos una hiperheurística paralela (HHP) basada en las metaheurísticas GA (Genetic Algorithm), SA (Simulated Annealing) y ACO (Ant Colony Optimization) como estrategias de bajo nivel. El objetivo global que se persigue es obtener un método que sea capaz de resolver diferentes instancias asociadas a problemas de localización y transporte. Esta hiperheurística opera a un nivel superior al de las técnicas metaheurísticas, de las cuales se asiste para guiar la búsqueda.
Las metaheurísticas no aseguran la obtención de soluciones óptimas, ni desempeños similares para todos los problemas. De esta manera, al menos por ahora, no es posible establecer un ranking de las mejores técnicas. No existe una demostración de que una metaheurística sea superior a otra en todos los casos. En estas condiciones, el rendimiento de una metaheurística es analizado en función de la calidad de la solución obtenida y el tiempo que le demandó al método obtenerla. También es importante considerar la simplicidad del método. Un algoritmo sencillo contribuye a su verificación y mantenimiento. Y por sobre todas las cosas hace más simple su adaptación a problemas distintos.
A. Metaheurísticas aplicadas a HHP
Reeves [14] define un método heurístico como una técnica que encuentra buenas soluciones a un costo computacional razonable sin garantizar que sea óptima. Las heurísticas se empezaron a usar a partir de los años 60, y se fundamentan en su capacidad práctica para solucionar problemas combinatorios reales de difícil resolución. Merece destacarse la forma en que ha crecido el uso de procedimientos heurísticos en los últimos años.
Su utilización se recomienda cuando, por la naturaleza del problema, no existe un método exacto de resolución o si bien existe, este emplea un tiempo excesivo de cómputo para ofrecer la solución. También puede utilizarse como complemento a un método exacto, por ejemplo, cuando se necesita de una buena solución inicial. En otros casos, se requiere incorporar a un modelo algunas condiciones que son difíciles de hacer en un método exacto. Entonces, se aprovecha la flexibilidad de los métodos heurísticos y se resigna una solución óptima por una aproximada a cambio de una versión más realista del modelo.
En particular, se denomina metaheurística a una estrategia de alto nivel que sirve de guía a otras heurísticas para orientar la búsqueda. Una característica que debería ser común a toda buena metaheurística, consiste en un balance entre un proceso de intensificación para explotar el espacio de búsqueda en las cercanías de una solución de buena calidad, y un proceso de diversificación para explorar diversas regiones del espacio de búsqueda [15]. El balance entre exploración y explotación afectará directamente la calidad de la solución encontrada y el tiempo utilizado para obtenerla.
La elección de las metaheurísticas incorporadas en HHP se basa en nuestra experiencia sobre su utilización, en donde observamos que las metaheurísticas basadas en trayectorias (SA) responden mejor al proceso de intensificación, y las técnicas que utilizan poblaciones de soluciones (GA y ACO) realizan una mejor diversificación de la búsqueda. Esto implica mejores tiempos computacionales para la primera, pero a cambio de una mayor probabilidad de quedar atrapado en un óptimo local.
Respecto a los tiempos de cómputo, también notamos ventajas de SA respecto a GA y ACO, remarcando nuevamente que los valores encontrados por SA son óptimos locales que muchas veces se ven superados por las soluciones de las técnicas poblacionales. Esta característica se ve acentuada cuando se configuran los algoritmos para que dispongan de un mayor tiempo de búsqueda. En lo que se refiere a la simplicidad del método, existe concordancia de que SA es uno de los métodos más sencillos y fáciles de implementar.
Se eligió incorporar GA, pues es un algoritmo evolutivo bien establecido por sus grandes ventajas, habiendo demostrado ser capaz de producir resultados sorprendentes ante el fracaso de las técnicas tradicionales de optimización [16]. La técnica ACO se inspira en la inteligencia colectiva de las comunidades de hormigas naturales. Consiste en un procedimiento que simula el mecanismo utilizado por las hormigas en su búsqueda de alimentos. Considera el depósito de feromona que dejan en el camino hacia la fuente de alimentos, que luego es utilizado para reflejar la experiencia adquirida en la búsqueda de la solución [17]. Con respecto a la técnica SA, se trata de un método de búsqueda que se fundamenta en el proceso físico de calentamiento de un sólido, seguido por un enfriamiento paulatino, hasta lograr un estado cristalino con una estructura casi perfecta [18].
B. Algoritmo Paralelo Hiperheurístico HHP
El algoritmo consiste en utilizar un conjunto de metaheurísticas como técnicas de bajo nivel de la hiperheurística. Una versión preliminar del diseño de esta propuesta fue presentada en Rodríguez et al. [19]; allí se propone el uso de SA y ACO como técnicas de resolución de bajo nivel de una hiperheurística. Durante su ejecución, la elección de la técnica a emplear se hacía al azar hasta tanto se cumpliera con la condición de parada. En la versión que presentamos en este artículo, varias mejoras se incorporaron con el objeto de perfeccionar el proceso de búsqueda. Así, se incorporó a la metaheurística GA como tercer método de resolución, con el objeto de obtener un mejor recorrido en el espacio de búsqueda.
Así pues, se implementó un mecanismo que guía la elección en función del estado de la búsqueda y el rendimiento observado en las últimas iteraciones. La hiperheurística lleva un control del resultado encontrado por cada algoritmo, de manera que cuando hay un estancamiento de la búsqueda en alguna de las técnicas se favorezca el uso de alguna otra. Además, cuando una técnica encuentra una mejor solución se activa un componente que privilegia la elección de la misma técnica para la próxima elección.
De igual manera, se desarrolló un proceso que realiza un intercambio de datos permitiendo que una técnica disponga de información descubierta por otra. Esta funcionalidad logra, por un lado, acelerar el proceso de búsqueda y por otro, también funciona como herramienta para escapar de óptimos locales.
La evaluación del estado del problema se hace en función del resultado encontrado por cada una de las técnicas en las últimas j ejecuciones. El valor j funciona como la dimensión de una memoria en la que se recopila información relacionada con:
1. La cantidad de veces que finalizó con éxito la ejecución, esto implica haber encontrado una mejor solución.
2. La cantidad de veces que no pudo mejorar la solución actual.
3. El tiempo que demandó obtener las últimas soluciones.
Con estas medidas de desempeño se asigna un valor de fuerza (peso) a cada metaheurística. De esta manera, es posible hacer que la técnica con mayor peso disponga de más chances de ser seleccionada para su ejecución.
Por último, se incorpora una estrategia paralela clásica basada en la ejecución de hilos. Así, cuando se cuenta con varios procesadores se pueden aprovechar las características de una hiperheurística haciendo que las técnicas de bajo nivel se ejecuten en simultáneo. De esta manera se logran disminuir los tiempos computacionales considerablemente.
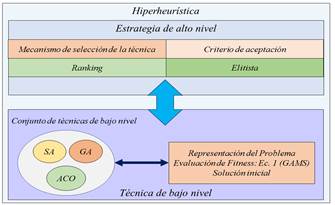
La hiperheurística tiene dos niveles, como se muestra en la Fig. 1, una estrategia de alto nivel y heurísticas de bajo nivel. La estrategia de alto nivel tiene dos componentes: mecanismo de selección heurística y criterio de aceptación. El componente heurístico de bajo nivel se compone de un conjunto de heurísticas que son específicas del problema y que pueden operar directamente sobre una solución dada para mejorar su rendimiento.
Finalmente, cuando una técnica encuentra una mejor solución, se procede a compartir el resultado encontrado con las demás, de la siguiente manera: I) GA incorpora a la solución como un individuo más reemplazándolo por algún otro seleccionado al azar. II) ACO aumenta la cantidad de feromona en el recorrido asociado a la solución encontrada. III) SA adopta la nueva solución como inicial.
Las tres metaheurísticas funcionan utilizando la misma función de aptitud, que es evaluada en este caso mediante el resolvedor GAMS [20]k (Fig. 1), uno de los lenguajes de modelado más difundido entre los investigadores. El flujo de información entre la hiperheurística y las metaheurísticas intervinientes no contiene información referida al problema. Este vínculo es para intercambiar información respecto a las soluciones encontradas y a los recursos utilizados para obtenerla.
El proceso de evaluar una solución con el objeto de obtener su valor de fitness, es una cuestión importante en toda técnica metaheurística. Es un proceso que afecta directamente al tiempo de cómputo puesto que se debe ejecutar cada vez que se necesita evaluar una solución propuesta por el algoritmo. Muchas veces ocurre que se generan soluciones que ya fueron evaluadas anteriormente derivando en un gasto innecesario de recursos. Se pretende que sea un proceso rápido y se realice la menor cantidad de veces posibles. En resumen el pseudo algoritmo correspondiente es:
Algoritmo HHP
Sact:=Inicializar();
Mientras no se cumpla condición Parada
Estado:= EvaluacionEstado();//
H:= EleccionTecnica();
EjecutarTecnica(H);
CompartirInformacion(fitness,H);
Fin Mientras
En este sentido, el algoritmo propuesto realiza dos acciones importantes. Por un lado, mantiene una memoria auxiliar con los registros de las últimas ejecuciones. Así, antes de llamar al módulo que evalúa una solución consulta si dicha solución está en la memoria auxiliar. Por otro lado, la acción de encontrar una nueva mejor solución y compartirla con las demás técnicas hace que el proceso de búsqueda sea más rápido y se reduzca la cantidad de evaluaciones realizadas.
Respecto al paralelismo, cuando existe la necesidad de disminuir los tiempos de cómputos, desarrollar algoritmos que se ejecutan en paralelo resulta una opción adecuada. La posibilidad de contar con múltiples procesadores permite implementar una programación basada en hilos, de manera que dos o más procesos se ejecuten de manera simultánea, uno en cada hilo.
La hiperheurística propuesta está preparada para funcionar en una plataforma que soporte múltiples hilos, con el fin de ejecutar cada uno de ellos en un procesador disponible. De esta manera, para cada hilo se selecciona una metaheurística y se procede con su ejecución hasta finalizar, momento en el que se reportan los resultados obtenidos. En dicho momento se procede con el intercambio de información hacia las demás técnicas que podrían estar en plena ejecución, razón por la cual se necesita un proceso de sincronización para coordinar el acceso a los datos compartidos y así evitar inconsistencias en el sistema.
III. SOBRE EL CASO DE ESTUDIO
Para el desarrollo de este trabajo se eligió una región de la ciudad de Bahía Blanca (Argentina) como caso de estudio, a partir de la premisa de que la racionalidad/eficiencia del transporte aumentará sensiblemente gracias a la optimización de recorridos mediante la hiperheurística presentada.
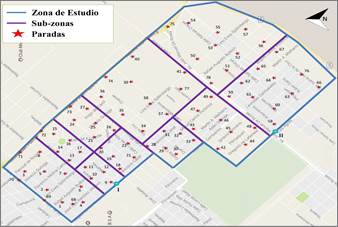
Se abordada un problema práctico que contribuye a la construcción de un sistema eficiente en el traslado de las personas que utilizan el transporte público. Este servicio lo brindan dos empresas, cada una de las cuales cuenta con una capacidad limitada de vehículos. La Fig. 2 muestra la zona de estudio, la cual se desea optimizar. La misma está dividida en zonas que contienen un determinado número de paradas a las cuales están asignados los pasajeros.
El objetivo de este análisis es dual. Por un lado, se pretende que ambas empresas logren maximizar sus beneficios por los servicios prestados. Por otra parte, se desea generar una ruta mejorada para el pasajero, quien necesita un servicio ágil y confiable. Se desea minimizar una función f de costos (1), la cual tiene asociada un conjunto de variables de diseño {p1, p2,…, pn} que permiten definir el ruteo
El requerimiento empresarial consiste en determinar las paradas a utilizar, la asignación de los pasajeros a estas paradas (los pasajeros asignados a las paradas no utilizadas se asocian a la parada más cercana de las seleccionadas en su zona) y establecer las rutas de los autobuses para satisfacer la demanda de los pasajeros, minimizando el costo global y optimizando el servicio. El costo global f incluye los costos fijos de apertura de las paradas, los costos fijos asociados a los autobuses utilizados y los costos por recorrer los trayectos de las rutas establecidas. Los colectivos deberán atravesar la ciudad, partiendo y finalizando sus recorridos en la estación central, cuya ubicación ya se encuentra establecida.
IV. ANÁLISIS DE RESULTADOS
Los algoritmos fueron implementados en el lenguaje Java y los experimentos computacionales se ejecutaron en una PC Intel Core i5-3330 con 8 GB de RAM. La discusión de resultados que se efectúa a continuación, se realiza con base en los valores obtenidos a partir de 30 ejecuciones independientes en cada una de las técnicas.
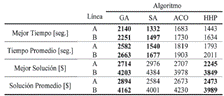
La Tabla I muestra los resultados obtenidos por HHP para el caso de estudio descrito. Se presenta la mejor solución encontrada, el costo asociado a dicha solución, el promedio de las soluciones obtenidas y el tiempo computacional demandado. En la solución propuesta, representada como la secuencia de paradas que el autobús debe recorrer para satisfacer la demanda de cada zona, se puede observar que se utiliza una sola parada de cada zona establecida.
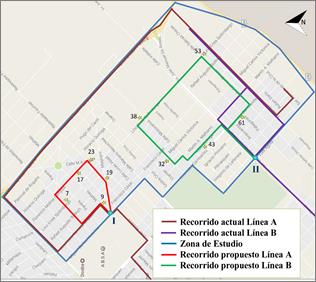
En la Fig. 3 se puede observar cuáles son los recorridos actuales y los propuestos por el algoritmo para cada una de las líneas de transporte. A los fines comparativos y con el objeto de valorar el rendimiento de la híperheurística propuesta, se resolvió el mismo problema con las tres metaheurísticas ejecutándolas de manera independiente. En la Tabla II se ofrecen detalles de los resultados alcanzados por las metaheurísticas GA, SA y ACO, los cuales se compararon con los resultados de HHP. La comparación se realizó en función de la mejor solución encontrada y de los tiempos computacionales incurridos.
Se pudo observar un rendimiento superior de la hiperheurística. HHP encuentra en todos los casos la mejor solución y además, tiene el mejor promedio de las soluciones obtenidas. Respecto al tiempo de cómputo, solo es apenas superado por la técnica SA. Por otro lado, se propuso considerar la cantidad de evaluaciones realizadas como una medida de comparación de rendimientos entre las técnicas. Este aspecto cobra especial interés cuando el proceso para valorar una solución consume muchos recursos. En este trabajo, cada vez que se necesita evaluar una solución propuesta por el algoritmo se resuelve un problema de transporte modelado en el software GAMS, por lo que una disminución en la cantidad de evaluaciones realizadas se ve directamente reflejada en el tiempo de cómputo utilizado.
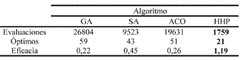
Además, se pretende maximizar el número de evaluaciones en las que se encuentran mejores soluciones. En definitiva, se desea conseguir la mayor cantidad de óptimos parciales durante una ejecución con un mínimo número de evaluaciones. Por lo tanto, un porcentaje de eficacia puede calcularse como el cociente entre la cantidad de óptimos y cantidad de evaluaciones. La Tabla III presenta la cantidad de evaluaciones realizadas por cada uno de los algoritmos, así como también la cantidad de veces que en una evaluación se alcanzó el óptimo. Vistos los porcentajes de eficacia, HHP supera a las tres metaheurísticas cuando se comparan con su ejecución individual.
Merece destacarse la diferencia existente entre las técnicas poblacionales GA y ACO, y la técnica basada en trayectorias (SA) en cuanto a la cantidad de evaluaciones que necesita cada una de ellas. Sin embargo, el esfuerzo computacional realizado por GA y ACO no se ve reflejado en el porcentaje de casos exitosos. En ese aspecto, se muestra un mejor rendimiento de SA y otro muy superior de HHP. También puede observarse que HHP necesita un número considerablemente menor de evaluaciones que las metaheurísticas estudiadas y además, obtiene un gran porcentaje de nuevas mejores soluciones en dichas evaluaciones.
V. CONCLUSIONES
Los resultados obtenidos en el problema abordado en este artículo demuestran la efectividad de emplear el algoritmo hiperheurístico. La hiperheurística logra un alto rendimiento en la búsqueda de soluciones, superando ampliamente a los obtenidos con las metaheurísticas GA, SA y ACO. En primera instancia, se destaca que HHP es capaz de obtener soluciones de mejor calidad empleando menos tiempo de cómputo. Los valores medios exhibidos indican que estas condiciones se presentan en la gran mayoría de las ejecuciones realizadas, demostrando la robustez del algoritmo.
De igual modo, se destacan las contribuciones de los mecanismos de intercambio de información entre las técnicas y el de control y selección de la técnica. El primero permite acelerar la convergencia en el proceso de búsqueda y el segundo procura mejorar el escape de óptimos locales. Además, se resalta que con este enfoque cooperativo se puede disminuir la cantidad de soluciones que es necesario evaluar, a la vez que se aumenta el porcentaje de veces en que se encuentra una mejor solución durante la ejecución de la hiperheurística.
Finalmente, el presente trabajo forma parte de un proyecto conjunto con la Municipalidad de Bahía Blanca, cuyo objetivo es mejorar el transporte de la ciudad (Proyecto CIC: PIT-AP-BA - Resol. Nº 428/16 y/o 429/16). El siguiente paso es la obtención de información actualizada mediante encuestas relacionadas con la demanda de pasajeros, para lo cual se utilizará el software con el fin de obtener resultados mediante datos actualizados.