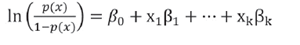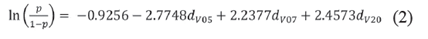I. NOMENCLATURA
FCEFN - Facultad de Ciencias Exactas, Físicas y Naturales.
FFHA - Facultad de Filosofía, Humanidades y Artes.
UNSJ - Universidad Nacional de San Juan.
II. INTRODUCCIÓN
En muchas investigaciones, independientemente del área de conocimiento, es habitual contar con la necesidad de identificar cuáles son las características que diferencian ciertos grupos de sujetos u objetos respecto de otros, para así contar con predicciones futuras [1].
Este trabajo tiene como propósito esencial mostrar los resultados obtenidos en la determinación de variables que mejor explican la atribución de la diferencia de los grupos de alumnos universitarios de la FCEFN y FFHA de la UNSJ, según su buen o mal rendimiento. Para ello se aplican técnicas del Análisis Multivariado (AM), a datos provenientes de una encuesta titulada: “Encuesta de factores de riesgo y calidad de vida de estudiantes universitarios”, realizada a alumnos de dichas facultades.
El Análisis Factorial de Correspondencias Múltiples (AFCM) es una herramienta del AM de gran utilidad en la investigación por encuestas, tanto por su potencial en términos exploratorios como por su adecuación para el tratamiento de variables categóricas. Permite establecer las relaciones (correspondencias) que existen entre las variables (y entre sus modalidades). Puede interpretarse como una manera de representar las variables en un espacio de dimensión menor, mediante la definición de ejes factoriales y utilizando la métrica Chi-cuadrado. También, como un procedimiento objetivo de asignar valores numéricos a variables cualitativas [2].
Por otro lado, tanto el Análisis de Conglomerados como el Análisis Discriminante, a lo que algunos autores ubican entre las técnicas estadísticas del AM más potentes para aplicar en investigaciones sociales, son técnicas que permiten clasificar sujetos u objetos a partir de características similares. Las técnicas mencionadas se pueden diferenciar de acuerdo con la forma de extraer conocimiento útil, escondido en esos datos. El Análisis Discriminante cuenta con grupos de datos conocidos, así como observaciones de unidades cuya pertenencia a los grupos, en términos de los grupos conocidos, es desconocida inicialmente y tiene que ser determinada a través del análisis de los datos. Este tipo de problemas de clasificación es comúnmente conocido como reconocimiento de patrones asistido, o aprendizaje con una guía. En terminología estadística, se conoce con el nombre de “Análisis Discriminante” (AD).
De otro lado, existen problemas de clasificación donde los grupos son ellos mismos desconocidos a priori y el principal propósito del análisis es determinar los grupos a partir de los propios datos, de modo que las unidades dentro del mismo grupo sean en algún sentido más similares u homogéneas que aquellas que pertenecen a grupos diferentes. Este tipo de problema de clasificación es referido como reconocimiento de patrón no supervisado o conocimiento sin guía, y, en terminología estadística, se conoce con el título de “Análisis de Conglomerados” (AC).
De otro lado, se puede afirmar que, en general, un indicador directo de la calidad de la enseñanza es el rendimiento académico medido a través del nivel alcanzado por los estudiantes [3]. Así, dicho rendimiento del estudiantado universitario constituye un factor imprescindible en el abordaje del tema de la calidad de la educación superior. Vista la importancia del tema, en este trabajo se aplican y complementan las distintas técnicas mencionadas para analizar y caracterizar lo que se denomina rendimiento académico universitario desde la perspectiva del alumno.
III. METODOLOGÍA
Teniendo en cuenta que se quiere caracterizar el rendimiento académico hallando tipologías del alumnado, como también determinar variables influyentes y definir una función discriminante que explique el rendimiento de los alumnos universitarios a partir de dichas variables, se organiza el presente trabajo en dos etapas:
1) Caracterización del alumnado según su perfil de rendimiento.
2) Definición y evaluación de modelos que permitan identificar variables influyentes y discriminar a alumnos según su rendimiento.
Para tal efecto, se realiza un estudio exploratorio uni y bidimensional de los datos de la encuesta. Como existe una evidente asociación de las variables tratadas, es necesaria la aplicación de técnicas del AM. La información proveniente de la encuesta incluye preguntas relacionadas con el rendimiento académico del estudiante. La encuesta fue elaborada con la herramienta web de encuestas online, EncuestaFácil.com, y cuenta con varias secciones. Las variables consideradas se pueden agrupar en: variables que caracterizan la Facultad, la universidad y la carrera/s que cursa el estudiante; variables que representan características personales del estudiante y de su familia (edad, sexo, su relación con pares, etc.). Variables asociadas al rendimiento (rendimiento, promedio, etc.); y variables que representan el esfuerzo y motivación del estudiante (Ej. hs. de estudio, asistencia a la universidad, etc.). Se puede consultar la encuesta en:
https://www.encuestafacil.com/RespWeb/Qn.aspx?EID=2197195.
Las preguntas consideradas no son mutuamente excluyentes entre sí, por lo que cada pregunta es una variable en sí misma; las respuestas alternativas a las preguntas de cada sección sí son mutuamente excluyentes y cada una de ellas es una modalidad de las variables cualitativas a las que pertenece. En este trabajo, cada encuestado no interesa en sí mismo sino como representante de cierta categoría o grupo de población. En la primera etapa, mediante el AFCM y un AC, se busca encontrar la tipología de los alumnos según su perfil de rendimiento y su caracterización. Dos alumnos son próximos si poseen buen rendimiento o no, y si tienen similares características según las variables consideradas. Con el AFCM se pretende: hallar la semejanza de los alumnos; estudiar la relación entre las variables; resumir las características observadas en un pequeño número de variables; y comparar modalidades de diferentes variables.
Se distinguen dos ámbitos: el que concierne al estudio de cómo se agrupan los alumnos teniendo en cuenta su rendimiento académico, y las variables más asociadas. A estas variables se les llama en este artículo: “variables activas” en la conformación de los clúster en el AC. El segundo ámbito es relativo a otras variables, distintas de las activas, a las que denominan los autores: “variables suplementarias”, que pueden contribuir con la caracterización de los grupos de alumnos predefinidos, en otros aspectos que pueden ser relevantes.
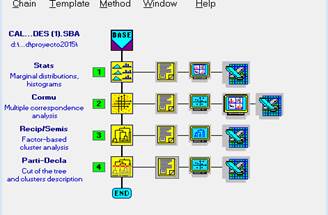
Una vez que se obtienen los factores que concentran la mayor proporción de inercia, mediante el AFCM, se puede aplicar un AC. Dicho análisis trata, a partir de una tabla de datos (individuos-variables), de situar a los individuos en grupos homogéneos o conglomerados, de manera que los que se puedan considerar similares, sean asignados a un mismo clúster o grupo. Tanto el AFCM como AC se realizan con la ayuda del software estadístico SPAD-N, siguiendo los pasos indicados en la Fig. 1. SPAD (Système Portable pourl’Analyse de Données) permite implementar una estrategia de análisis adecuada al tratamiento exploratorio multivariante de grandes tablas de datos. Su concepción es original y adaptada para un proceso natural de aprendizaje a partir de los datos (data learning) [4]. La existencia de asociación entre variables se puede pensar como una fuente de oportunidades para plantear Modelos de Discriminación. El objetivo es definir un modelo para clasificar mediante la construcción de un Modelo de Regresión Lineal Generalizado (MLG), tal que a partir de una observación “x” de n-variables asociadas al rendimiento académico del alumno, proporcione la probabilidad de que el rendimiento académico sea, por ejemplo, malo (éxito).
Dicho modelo se construye maximizando la probabilidad de la muestra. A través de un Modelo de Regresión Logística (MRL) se puede estimar la probabilidad de un suceso que depende de los valores de ciertas covariables o variables asociadas. En la segunda etapa de este estudio, el suceso (o evento) de interés es A: “El Rendimiento Académico del alumno es malo”, que puede presentarse o no en cada uno de los alumnos de la población donde se realizó la encuesta. Se considera la variable binaria “y” (de tipo Bernoulli) que toma los valores: y = 1, si el suceso A se presenta; y = 0, si A no se presenta. Sea p la probabilidad de que y=1, en un ensayo. Suponiendo que la probabilidad p depende de los valores de ciertas variables, X1,… ,Xk; si son las observaciones correspondientes a un alumno sobre las variables, entonces la probabilidad de acontecer A dado x es p(y=1/x) que simbolizamos con p(x). La probabilidad de que no suceda A dado x será p(y = 0/x) = 1-p(x).
Teniendo en cuenta los valores en que varía p(x) y el tipo de variables explicativas en este estudio, resulta conveniente suponer un modelo lineal con la llamada transformación logística de la probabilidad (1), siendo los 1≤i≤k, con los parámetros del MRL.
Según Díaz y Demetrio [5], el objetivo en el proceso de ajuste de un MLG determinado debe ser obtener el mejor trade-off entre el número de variables y sus parámetros, que deben incluirse en la estructura lineal, manteniendo el menor número posible de ellos y la habilidad del modelo para representar a los datos, conservando el ajuste lo más adecuado posible.
Como test de ajuste de un modelo MLG, primeramente se observa el estadístico deviance [6], diferencia entre los máximos de los log-verosimilitud para el modelo saturado y en investigación (modelo con k parámetros), esto es, 𝐷=2( 𝐿 𝑛 − 𝐿 𝑘 ). Otra expresión para este estadístico es S k = D(y, 𝑢 ) ϕ , conocido como la deviance para el modelo de investigación. Para ver si un modelo ajusta bien, se compara el valorSk con el punto crítico de la χ (n−k)gl 2 , para un nivel de significación α. Luego si S k >𝜒 (n−k)gl;α 2 el modelo de investigación es rechazado. Para analizar la contribución de un término más en el modelo, se emplea la diferencia de deviances, S k − S q , la cual debe ser comparada con el punto crítico de la χ (q−k)gl 2 para ese nivel α. También se utiliza la cantidad denotada con AIC, de la formaD+2k ϕ presentada por Chambers y Hastie, con ϕ parámetro de escala [7].
Para determinar un MRL se aplica la función genérica “glm” del programa R. Como el modelo de discriminación no es único, es conveniente evaluar y comparar resultados. Para ello se aplica el método Hold-out que tiene en cuenta las tasas de errores en la clasificación (APER), tanto en la muestra para definir el modelo, como en la muestra test. La tasa de error aparente se define como la fracción de observaciones en las muestras de entrenamiento, clasificadas erróneamente por la función de clasificación muestral, determinada por 𝐴𝑃𝐸𝑅= 𝑛 1𝑀 + 𝑛 2𝑀 𝑛 1 + 𝑛 2 , donde 𝑛 1𝑀 es el número de observaciones de la población 1, clasificado erróneamente como observaciones de la población 2 y 𝑛 2𝑀 ; el número de observaciones de la población 2 clasificados erróneamente como observaciones de la población 1 [8]. En este estudio, la selección de la muestra para el entrenamiento se determinó de forma aleatoria a partir de una rutina “simple” del programa R, y representando aproximadamente el 70% del total de datos de la encuesta.
IV. DESARROLLO Y RESULTADOS
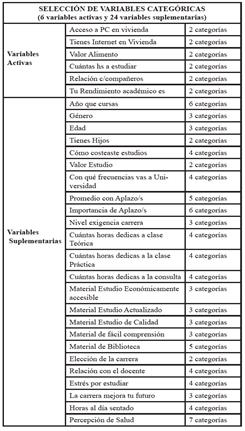
A partir de la puesta en práctica de una encuesta sobre factores de riesgo y calidad de vida a 74 alumnos universitarios pertenecientes a la FFHA y FCEFN de la UNSJ, donde aproximadamente el 88% afirma tener “buen rendimiento académico”, y el 12% “mal rendimiento”, se quiere caracterizar a los alumnos en cuanto a su rendimiento, con el objetivo de identificar grupos y diferenciarlos, con base en el análisis de variables asociadas, utilizando las técnicas estadísticas del AC y el Análisis de Discriminación Logística. En la base de datos se pueden distinguir 95 variables; se trabaja con 30 de ellas que se consideran más adecuadas para la caracterización del rendimiento académico del estudiante de ambas facultades; 6 de las variables se seleccionan como “variables activas” para la construcción de los clúster o grupos. Las 24 variables restantes se consideran “variables suplementarias” para caracterizar a los grupos. Las variables seleccionadas son todas categóricas y el número de modalidades o categorías quedan detalladas en la Tabla I.
El criterio de selección de cada variable categórica como activa, fue a través de observar evidencias, bajo un nivel de significación del 5% en la asociación de la variable seleccionada y la variable rendimiento académico. Esto requirió previamente del análisis y la transformación de la base de datos en forma conveniente. Se combinaron categorías de una misma variable cuando las frecuencias observadas resultaron menores a 5, y se aplicaron pruebas Chi-cuadrado de independencia para tablas de contingencias dos por dos. En total se realizaron 29 pruebas utilizando el software SPSS. Estas variables, así seleccionadas, son las que van a intervenir en la definición de los ejes factoriales (Tabla II y Tabla III), en el AFCM.
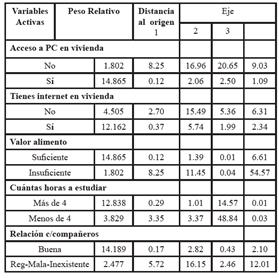
En las Tablas II y Tabla III se muestran algunos resultados del AFCM correspondiente a la primera etapa de trabajo. Del análisis se observa:
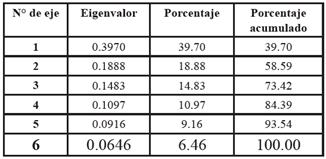
• Para el primer eje factorial, las variables activas que más peso ejercen sobre el eje, y concentran mayor cantidad de inercia son: “Tu Rendimiento Académico es” (contribución 23.6); “Tienes Internet en vivienda” (contribución 21.2); “Acceso a PC en vivienda”; y “Relación con compañeros” (las dos últimas con contribución 19). Los valores de los cosenos al cuadrado de cada modalidad, en la medida en que se aproximan al valor 1, indican buena calidad en la representación de la modalidad en el eje, por lo que todas las modalidades quedan bien representadas en el eje. Las modalidades de mayor peso ubicadas en el semieje positivo son: “Bueno” (respecto a la variable “Rendimiento Académico”); “Sí” (tiene Internet en su vivienda); “Sí” (tiene acceso a PC en vivienda), y “Buena” (relación con compañeros). En el primer eje factorial, que reúne el 39.70% de la inercia total de la nube de puntos (ver Tabla II), se oponen los alumnos que: tienen buen rendimiento, PC e Internet en vivienda, y consideran llevar buena relación con sus compañeros; con aquellos que poseen mal rendimiento, no tienen acceso a PC ni a Internet en su vivienda y llevan mala, regular o ninguna relación con sus compañeros.
• En el factor 2 la variable relevante es “Cuántas horas le dedica a estudiar” (contribución 63.4). Teniendo en cuenta los valores de los cosenos al cuadrado, las dos modalidades de dicha variable quedan bien representadas. El segundo eje, que reúne el 18.88% de la inercia total (ver Tabla II), contrapone los alumnos que le dedican más de 4 horas de estudio diario a la carrera (representado en el semieje positivo), respecto a aquellos que le dedican menos (representado en el semieje negativo).
• El tercer eje factorial, que reúne el 14.83% de la inercia total, la variable más relevante es “Valor alimento”, con una contribución 61.2.
Teniendo en cuenta las proyecciones de calidad en el primer plano factorial de las modalidades de las variables suplementarias, las cuales se pueden identificar a través de los valores-test mayores a 1.96 (en valor absoluto), que conducen a rechazar la hipótesis aleatoriedad con un nivel de significación de 0.05, se observa que: las variables suplementarias relacionadas con el primer eje factorial son “Año que cursas”, “Edad”, “Cómo costeaste estudios”, “Promedio con aplazos”, “Valor Estudio”, “Importancia de los aplazos”, “Cuántas horas le dedica a la práctica”, “Material de Biblioteca” y “Relación con el docente”.
Los alumnos cuyo rendimiento académico es bueno, tienen PC e Internet en vivienda, suficiente dinero para alimento y estudio, dedican más de 4 horas diarias a estudiar, tienen buena relación con compañeros y docentes, cursan tercer año, su edad oscila entre los 18 y los 24 años, costean los estudios solo con aporte, y el promedio con aplazos es mayor a 8. Se oponen a aquellos que poseen mal rendimiento, no tienen PC ni Internet en vivienda, es insuficiente el dinero para alimento y estudio, le dedican menos de 4 horas a la práctica y a estudiar, expresan que su relación con compañeros es regular, mala o inexistente, cursan cuarto año, la edad oscila entre 24 a 29 años, costean el estudio solo con trabajo, sienten mucho fracaso cuando lo aplazan, consideran que el material de Biblioteca es de difícil acceso y su relación con docentes es regular.
Mediante el AC se clasifican los alumnos de acuerdo con su similitud, por clasificación jerárquica, utilizando el método del vecino más próximo, considerando los primeros tres ejes factoriales que reúnen una inercia total acumulada del 73,42% aproximadamente. A partir de ella se obtiene la representación gráfica del proceso del agrupamiento mediante un Dendograma, en la que se pudieron distinguir dos grupos.
La primera clase o grupo la componen 12 alumnos, que representan el 6,22% del total de los alumnos encuestados. Se destacan por: no poseer internet en vivienda (55% del total de alumnos de esta modalidad forman esta clase, y el 91.67% de los alumnos de la clase no tienen internet en su casa); no tienen acceso a PC en vivienda (87.50% del total de alumnos de esta modalidad forman esta clase, y el 58.33% de los alumnos de la clase no tienen acceso a PC en vivienda); su rendimiento académico es malo (77.78% del total de los alumnos que presentan esta modalidad; representa el 58.33% de los alumnos de la clase no tienen buen rendimiento); su relación con compañeros es regular, mala o inexistente (63.64% del total de los alumnos que presentan esta modalidad; representa el 58.33% de los alumnos de la clase tienen esta modalidad); el dinero para alimento y estudio considera que es insuficiente (75%, 28.57% del total de alumnos que presentan cada modalidad; 50%, 83.33% de los alumnos de la clase tienen la modalidad, respectivamente); cursan cuarto año (71.43% del total de los alumnos que presentan esta modalidad; representa el 41.67% de los alumnos de la clase tienen esta modalidad); Cuentan entre 24 a 29 años de edad (36% del total de los alumnos que presentan esta modalidad; representa el 75% de los alumnos de la clase tienen esta modalidad); sienten mucho fracaso con los aplazos (31.03% del total de los alumnos que presentan esta modalidad; representa el 75% de los alumnos de la clase tienen esta modalidad); y considera que su relación con los docentes es regular (36.84% del total de los alumnos que presentan esta modalidad; representa el 58.33% de los alumnos de la clase tienen esta modalidad).
La segunda clase reúne el 83.78% del total de los alumnos encuestados, que se caracterizan por: poseer Internet en vivienda (98.15% del total de alumnos de esta modalidad; 85.48% de los alumnos de la clase); tener acceso a PC en vivienda (92.42% del total de alumnos de esta modalidad; 98.39% de los alumnos de la clase); tener buen rendimiento (92.31% del total de alumnos de esta modalidad; 96.77% de los alumnos de la clase); su relación con compañeros es buena (92.06% del total de alumnos de esta modalidad; 93.55% de los alumnos de la clase); consideran que tienen suficiente dinero para alimento y estudio (90.91%, 94.87% del total de alumnos que presentan cada modalidad; 96.77%, 59.68% de los alumnos de la clase tienen la modalidad, respectivamente); costean los estudios solo con aporte (100% del total de alumnos de esta modalidad; 43.55% de los alumnos de la clase); su edad está entre los 18 y los 24 años (95.12% del total de alumnos de esta modalidad; 62.90% de los alumnos de la clase); y su promedio con aplazo es mayor a 8 (100% del total de alumnos de esta modalidad; 35.48% de los alumnos de la clase).
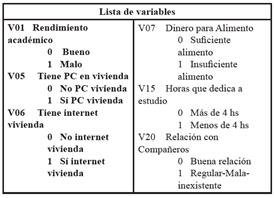
En la segunda etapa de trabajo, para definir un modelo de discriminación mediante MRL, se dispone de la información proveniente de la encuesta, para las variables categóricas cuyas modalidades se definen en la Tabla IV.
Se confecciona un programa en R cuyos pasos se pueden resumir en los siguientes:
Lectura de la base de datos.
Categorización de las variables explicativas (V05, V06, V07, V15 y V20).
Categorización de la variable respuesta (V01).
Selección de una muestra de entrenamiento y una muestra test.
A partir de la muestra de entrenamiento se realiza la estimación de los parámetros, y las pruebas de ajuste para el modelo con todas las variables y el modelo de investigación.
Confección de tablas de datos mal clasificados, para la muestra de entrenamiento y test.
Cálculo de tasas aparentes asociadas a la muestra de entrenamiento y test.
Cálculo de odds radio al modelo reducido para interpretar los coeficientes del modelo.
En la parte izquierda de la Tabla V, se observa el resultado de realizar el ajuste por máxima verosimilitud con el software R, considerando todas las variables de la Tabla IV. Los contrastes sobre los parámetros se realizan a través de tests de Wald. La función “glm” devuelve automáticamente el estadístico y la significación del test de Wald para cada parámetro del modelo.
Como la deviance residual S k =23.966 es menor que el valor crítico χ (n−k)gl;α 2 = χ 47gl;α=0.05 2 =64.00111, se puede asumir que el modelo ajusta bien, con un nivel de significación α=0.05. Luego se aplica el método paso a paso hacia atrás, para analizar si se puede hallar un modelo más simple que el antes fijado. Para ello se utiliza la rutina step de R. Inicialmente se tiene un AIC=33.97 para el modelo con todas las variables, y la función de R considera la eliminación de cada una de las variables para finalmente sacar del modelo la variable V06: “Tiene internet en su casa” por ser la que produce un AIC más bajo (32.16).
TABLA V Resultados del ajuste del modelo con todas las variables (izquierda) y del modelo reducido (derecha), utilizando la rutina glm de R.
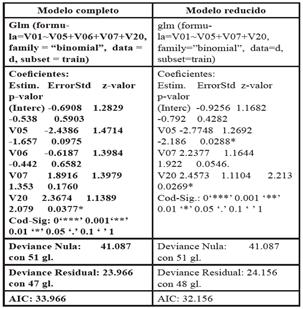
En el siguiente paso se considera la eliminación de alguna de las tres restantes variables, pero el algoritmo en R decide quedarse con ellas ya que su eliminación supone un aumento, en el mejor de los casos, del AIC último hallado. Como los valores de AIC no difieren mucho, entre el modelo con todas las variables y el modelo reducido, se analiza además la inclusión o no de la variable V06 realizando una prueba de significación mediante una prueba de razón de verosimilitudes. A partir de este modelo bajo un nivel de significación del 5%, como G=Deviance (modelo reducido) - Deviance (modelo con todas las variables)=25.881-25.867=0.014, resulta menor que el valor crítico 𝜒 1𝑔𝑙 2 =3.841459; por lo tanto, se puede considerar que la inclusión de la variable V06 no contribuye al modelo.
De acuerdo con los resultados más a la derecha en la Tabla V, se pueden observar los parámetros estimados y su significación en el modelo reducido. El MRL reducido se observa en (2).
Donde p representa la probabilidad de que la variable V01: “Rendimiento Académico” tome la categoría 1 (“Mal Rendimiento”) d V05 , d V07 y d V20 , variables dummy que toman el valor 1 cuando la modalidad que se observa corresponde a la categoría 1; en caso contrario, las variables toman el valor 0.
Sea β 0 + X i . β el segundo miembro del modelo reducido planteado, donde 𝑋 𝑖 =( d V05 , d V07 , d V20 ), 𝛽 0 =−0.9256 y 𝛽 =(−2.7748,2.2377,2.4573 ) 𝑇 vector de parámetros estimados. Si el “Alumno i” tiene 𝑥 𝑖 como vector de observaciones asociadas a las variables del modelo, 𝑝 ( 𝑥 𝑖 ) = 1 1+ 𝑒 𝛽 0 +𝑋 𝑖 . 𝛽 ⇒ 𝑞 ( 𝑥 𝑖 ) =1− 𝑝 ( 𝑥 𝑖 ) = 𝑒 𝛽 0 + 𝑋 𝑖 . 𝛽 1+ 𝑒 𝛽 0 +𝑋 𝑖 . 𝛽 . se definen como reglas para la clasificación: “Si 𝑒 𝛽 0 + 𝑋 𝑖 . 𝛽 1+ 𝑒 𝛽 0 +𝑋 𝑖 . 𝛽 >0.5, entonces el Alumno i pertenece a la clase de los de “Buen Rendimiento”, caso contrario a los de “Mal Rendimiento”.
La Tabla VI representa la tabla de mal clasificados para la muestra de entrenamiento y muestra test, al aplicar el modelo reducido estimado con R. A partir de la tabla se pueden calcular los errores aparentes correspondientes, resultando: 0.07692308 y 0.0909091 respectivamente. Por lo que el porcentaje de mal clasificados para la muestra de entrenamiento es de 7,69%, y para la muestra test de 9,09%. Ambos errores resultan similares, conservando un equilibrio en la proporción de errores, donde supera levemente el error aparente de la muestra test sobre el de la muestra de entrenamiento.
Los coeficientes estimados del modelo reducido se pueden interpretar mediante cocientes de chances. Para ello, se calculan los exponenciales de los coeficientes estimados y sus valores recíprocos en caso de que los exponenciales resulten valores menores a uno. De lo que resulta: si las modalidades “posee suficiente dinero para alimento” y “tiene buena relación con sus compañeros” se mantienen fijas, la chance de que un alumno tenga mal rendimiento, respecto a que tenga buen rendimiento, es 1/ 𝑒 −2.7748 ≅16 veces mayor, si el alumno no tiene acceso a PC en casa, respecto al que sí tiene acceso.
Ahora, si se mantienen fijas “no tiene acceso PC en su casa”, y “tiene buena relación con sus compañeros”, la chance de que un alumno no tenga buen rendimiento, respecto a que sí lo tenga, es 𝑒 2.2377 ≅9.371751 veces mayor si “no tiene suficiente dinero para alimento” respecto al que tiene suficiente alimento. Por último, si se mantienen fijas “no tiene acceso a PC en su casa” y “tiene suficiente dinero para alimento”, la chance de que el alumno no tenga buen rendimiento, respecto al que sí lo tenga, es 𝑒 2.4573 ≅11.67325 veces mayor si el alumno tiene una relación regular, mala o no tener relación con sus compañeros, respecto al que tiene una relación buena.
V. CONCLUSIONES
Mediante un análisis discriminante se pudo establecer el poder explicativo y discriminatorio de características que diferencian a los alumnos según su rendimiento, a partir de datos extraídos de una encuesta.
A través de la identificación de variables influyentes, mediante la aplicación de técnicas del AM, se pudieron vislumbrar aspectos sociales, culturales y económicos fuertemente asociados al rendimiento del estudiante universitario, y con ello a la calidad educativa, tales como: el disponer de PC en vivienda, el tipo de relación con sus compañeros, tener suficiente dinero para alimento.
Esta información relevante de los alumnos puede contribuir en la formulación de políticas de mejoramiento o direccionamiento institucional. Los resultados aportan herramientas que permitan realizar un diagnóstico válido para orientar de manera efectiva las intervenciones que realice la institución, en este sentido, para posteriormente diseñar una medida de seguimiento año a año mediante la aplicación sistemática del instrumento, con el objeto de evaluar el impacto de las acciones realizadas.