I. INTRODUCCIÓN
Los problemas que surgen en la enseñanza de la matemática hacen parte de un campo de investigación amplio, del cual se ha encargado la Didáctica de la Matemática a través de diferentes metodologías, marco teóricos y estrategias que han dotado de un sin número de posibilidades de investigación a docentes de matemáticas. Los filósofos Scheffler y Petrie, citados en [1], en la década de los sesenta y setenta, analizaron el papel de la metáfora en la educación; más adelante, Lakoff y Johnson en [2], pretendieron mostrar cómo, buena parte de la experiencia cotidiana del mundo y de las relaciones sociales, están estructuradas metafóricamente. Asimismo, durante las últimas dos décadas se han escrito artículos de investigación relacionados con el lenguaje metafórico y las implicaciones que este genera en el discurso de los docentes. Entre ellos [3], Lizcano manifiesta en su texto que el estudio sistemático de las metáforas puede emplearse como un potente analizador social, o el trabajo de [4], para quien la metáfora se constituye en una vía para entender la realidad.
En cuanto a la presencia de metáforas en el lenguaje matemático en el aula, Leger, Gálvez, Inostroza, Cubillos, Luci, Tanter, Cosmelli y Soto citados en [1], crean un software llamado ECOCAM, diseñado a partir del análisis de la actividad cognitiva basada en metáforas. Pochulu, Abrate y Font citados en [1] bajo el marco teórico de la metáfora conceptual, diseñan una secuencia de actividades para ser resueltas por los estudiantes, con el fin de analizar el discurso escrito que emplean los alumnos en contextos de resolución de ecuaciones. Acevedo citado en [1], hace un aporte con su tesis doctoral “Fenómenos relacionados con el uso de metáforas en el discurso del profesor. El caso de las gráficas de funciones”, en la cual busca comprobar que este fenómeno detectado por [5], ocurre con cierta regularidad. Asimismo, [6] son un referente teórico muy importante respecto al análisis de la presencia de metáforas y sus implicaciones cognitivas en el lenguaje de las Matemáticas.
Por otra parte, Romaña citado en [1], realiza el trabajo de maestría: “Posibles implicaciones del discurso metafórico docente en el abordaje del concepto de divisibilidad con estudiantes de séptimo grado de la institución educativa Santa Teresita del municipio de La Victoria (Valle del Cauca)”, con el grupo de investigación en Pensamiento Matemático y Comunicación-GIPEMAC en la Universidad Tecnológica de Pereira, en el cual aborda toda la teoría cognitiva de la matemática aplicada concretamente al concepto de divisibilidad.
A través de este breve recorrido, se resalta la importancia del análisis metafórico en el estudio de objetos matemáticos concretos con el objetivo de entender y mejorar la comunicación como elemento fundamental en la enseñanza de la matemática, pues es la metáfora un recurso didáctico que puede llegar a ser útil en la medida en que se logren dilucidar los elementos que constituyen su estructura.
Son muchos los factores que influyen en el proceso de enseñanza de las matemáticas, pues no solo se debe pensar en las condiciones dentro de las cuales el estudiante se encuentra en el aula de clase sino, también en las condiciones del docente, como actores principales del proceso de enseñanza aprendizaje. El principal canal mediante el cual se da la comunicación entre el docente y el estudiante es el lenguaje verbal. [15] considera que “Entre las matemáticas y el lenguaje escrito existe una relación especial: el razonamiento matemático depende de abreviaturas y símbolos y, para su desarrollo, hace falta utilizar la notación escrita, sin que pueda transferirse con facilidad al lenguaje hablado”. Este autor reconoce la dificultad presente cuando se pretende pasar del lenguaje hablado al lenguaje matemático, aunque señala la relación estrecha de este con el lenguaje escrito.
En principio, desde el punto de vista comunicacional, se pueden señalar dos dificultades en el aula. Una se presenta debido a que se enseñan y se aprenden los conceptos de manera mecánica cuando el docente realiza la trasposición didáctica, en términos de [8], al transformar el saber contenido en los libros especializados, dada la falta de comprensión exacta, por parte del profesor, del pensamiento metafórico del autor de dichos libros con relación al objeto de estudio. Otra dificultad se debe al pensamiento metafórico del profesor con el que pretende aclarar o explicar un concepto, dado que él solo puede hablar de lo que su imaginario social le permite entender [9], un imaginario del cual surgen las metáforas que constituyen ese pensamiento metafórico, como asegura [3].
En este orden de ideas hay que señalar que, inicialmente, los conceptos son tratados desde el lenguaje cotidiano empleado por el docente, hecho que permite considerar este canal como el primordial propulsor del fracaso de la comprensión de los objetos matemáticos en estudio. [7] dice que “las matemáticas son un lenguaje de modo especial, como una metáfora”, considera los elementos lingüísticos que frecuentemente utilizamos para referirnos a nuestra cotidianidad como un tratamiento especial que subyace en el lenguaje metafórico que diariamente se emplean en la comunicación. De igual manera lo hace el docente de matemáticas en su discurso, al emplear metáforas de manera inconsciente, con el fin de abordar objetos matemáticos que desde el uso de un lenguaje cotidiano y cultural, se esperaría que fuese más fácilmente comprensible para los educandos.
De esta manera, resulta evidente cómo el sistema conceptual humano está estructurado a través de las metáforas. Según [2]: “La metáfora impregna la vida cotidiana, no solamente el lenguaje, sino también el pensamiento y la acción. Nuestro sistema conceptual ordinario en términos del cual pensamos y actuamos, es fundamentalmente de naturaleza metafórica”. Esta concepción permite sustentar que el lenguaje metafórico hace parte de una práctica cotidiana, que, en el caso de la clase de matemáticas, indiscutiblemente, es difícil no utilizar, ya que este es innato a nuestra condición como canal de comunicación verbal. Esto deja en evidencia que el lenguaje del profesor está fundado en las metáforas que son clasificadas según su contexto de desarrollo cultural. [2] caracterizan las metáforas que se perciben en la vida cotidiana principalmente como: estructurales, orientacionales y ontológicas.
Teniendo en cuenta esta teoría, se presentan aquí los resultados al analizar el discurso utilizado en clase de matemáticas para enseñar el concepto de número complejo de dos profesores, uno licenciado en Matemáticas y Física de la Universidad Tecnológica de Pereira (UTP) y el otro Tecnólogo mecánico de la misma universidad, en grado noveno de la institución educativa Hogar Nazaret, en Dosquebradas (Risaralda).
II. MARCO TEÓRICO
La investigación se desarrolló en el marco de la Teoría Cognitiva de la Matemática y para el análisis de los datos se utilizó el Análisis de Contenido.
A. Teoría Cognitiva de la Matemática
La importancia que tiene el pensamiento metafórico en la construcción del significado de los objetos matemáticos es reconocida por diversos investigadores en didáctica de las matemáticas, y es el origen de una teoría del aprendizaje, propuesta realizada por [6]. Esta teoría, llamada Ciencia Cognitiva de las Matemáticas, presenta como núcleo la importancia que tiene el cuerpo sobre la mente y algunas investigaciones recientes en lingüística cognitiva. Su tesis afirma que el origen de las estructuras matemáticas que construyen las personas y las instituciones, hay que buscarlo en los procesos cognoscitivos cotidianos, como son los esquemas de las imágenes y el pensamiento metafórico.
Según [6], dichos procesos permiten explicar cómo la construcción de los objetos matemáticos, tanto los personales como los institucionales de los que habla [10], están sostenidos por la manera como el cuerpo se relaciona con los objetos de la vida cotidiana. Teniendo en cuenta este punto de vista, para [5], la naturaleza de las matemáticas hay que buscarla en las ideas de las personas, más no en las demostraciones y rigurosidades propias de las matemáticas.
B. Análisis de contenido
Este marco teórico implementa en la investigación como metodología, el análisis textual e intertextual del discurso del docente en un nivel semántico, que confecciona algunos apartes de lo sintáctico y pragmático desde la praxis del lenguaje utilizado por el docente en su discurso, durante la enseñanza del número complejo.
La técnica de análisis de los datos es conocida como análisis de contenido (AC), y según [11], este término se usa para referirse al proceso de recoger y resumir los datos escritos, es decir: “Los contenidos principales de los datos y sus mensajes. […] El análisis de contenido se puede llevar a cabo con cualquier tipo de material escrito, desde documentos a transcripciones de entrevistas”.
[12] señalan que: “Las expresiones verbales pueden producirse en dos formas distintas: como expresiones orales o como expresiones escritas. Se trata de dos modos de expresión verbal que suelen originarse en contextos diferentes, y que se rigen por reglas peculiares. Sin embargo y justamente para poder manejarlas con comodidad como “expresiones-objeto”, el análisis de expresiones orales se realiza normalmente a partir de transcripciones escritas de las mismas”. La transcripción del discurso con el marco teórico mencionado, constituye el análisis a nivel semántico de las expresiones utilizadas por el docente al tratar de enseñar el concepto de número complejo, considerando estas unidades lingüísticas como instrumento en la investigación.
Dentro de los niveles del AC, la investigación se centra en el nivel semántico, aunque no deja a un lado lo sintáctico y pragmático. El análisis temático permeado por los esquemas categoriales por medio de procedimientos estándares de codificación y categorización originarios de este tipo de análisis, son las técnicas más representativas del AC en el nivel semántico. El nivel semántico en su condición de vinculación con el nivel pragmático, interviene en los métodos más representativos de este, como son: la perspectiva instrumental, el análisis de la expresividad y el punto de vista conversacional. De estos, el más aludido con respecto a la intención de la investigación desde la semántica está dado bajo la perspectiva instrumental, ya que esta hace referencia a las circunstancias en las que se da la comunicación y su intencionalidad. [13] considera que el análisis debe iluminar al investigador acerca de la manera en que aquello que hay en la mente de los hablantes influye en la forma de la comunicación.
III. METODOLOGÍA
El estudio se centró en el análisis de registros de audio de dos docentes en el momento en que abordaban el concepto de número complejo con estudiantes de grado noveno. Mediante el estudio de dichos registros y la elaboración de entrevistas para docentes y estudiantes, se buscó determinar el tipo de incidencia del lenguaje metafórico en el aprendizaje del concepto de número complejo.
La metodología de investigación se implementó desde el análisis de contenido de tipo cualitativa-interpretativa, mediante el proceso de observación, elaboración de una entrevista estructurada y en el ámbito del método etnográfico. A la luz de dicho análisis, se observó qué tipo de incidencia generó el lenguaje que usó el docente en la clase, mediante el contraste de significados obtenidos.
A. Descriptores metodológicos
El desarrollo de la clase para el profesor 1, se dio en dos sesiones, cada una de 105 minutos: la primera el 18 de mayo de 2016 y la segunda el 24 de mayo de 2016.
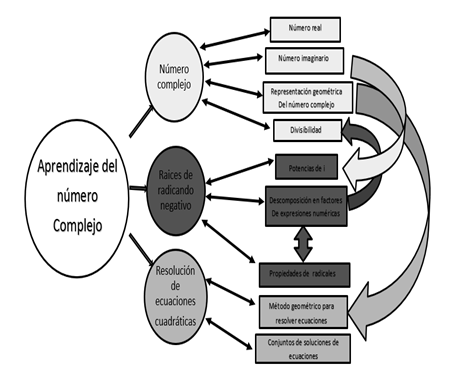
Una vez obtenidas las grabaciones de las clases, se realizó la transcripción de los audios de clase sin omitir detalle. Al tener la información digitalizada, se leyó el discurso identificando las expresiones metafóricas utilizadas en el desarrollo de las clases para la identificación de categorías de estudio, según la documentación referente y el marco teórico de la investigación. Se utilizaron colores para identificar el tipo de metáfora encontrada en el discurso del docente y generar las categorías de estudio. La categorización del discurso del profesor 1 se presenta en la Fig. 1.
En la Fig. 1 se evidencia la aparición de tres categorías, las cuales, a su vez, inducen la aparición de subcategorías que explicitan la funcionalidad de las categorías. En la lectura de la transcripción se notó cómo algunos elementos propios de una categoría se mezclaban con otras, por medio de la descripción de acciones en las subcategorías, es ese el sentido de las flechas relacionales en el diagrama. Un ejemplo de esto, es dado en la siguiente expresión: “Necesito hallar la raíz cuadrada de menos 18, ¿Cómo la puedo sacar?, vamos a cambiar el menos 18 y a darle la vuelta. Raíz de menos 18 es lo mismo que decir la raíz de 18 por menos 1, ahí ya los separé ya los tengo, y esto es lo mismo que decir la raíz cuadrada de 18 por la raíz cuadrada de menos 1.”
En esta expresión correspondiente a la categoría raíces de radicando negativo, se nota cómo el concepto de descomposición de números y divisibilidad se mezcla en una sola expresión con las propiedades de los radicales, mostrando la vinculación de dos subcategorías a través de una expresión metafórica.
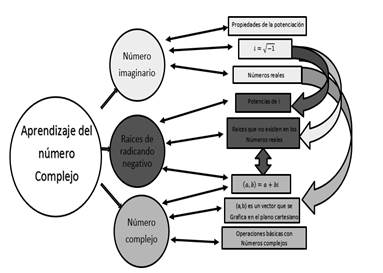
Para el profesor 2, el desarrollo de la grabación del audio se realizó en una clase de 56 minutos el 7 de julio de 2017. Luego se desarrolló el mismo proceso investigativo que para el docente 1, categorizando el discurso del profesor 2, como se ilustra en la Fig. 2.
En la Fig. 2 se observa cómo la concepción del número imaginario se conecta con la categoría de raíces de radicando negativo a través de las potencias de i; esto implica la conexión de cada categoría con subcategorías, como sucedió con el profesor 1. Ejemplos de esto se pueden notar a partir de la siguiente frase metafórica utilizada por el docente durante la clase: “Si tenemos −1 y lo elevamos al cuadrado, eso es lo que yo tengo ahí, i al cuadrado es lo mismo que tener: ( −1 ) 2 y resulta que esta raíz que es cuadrada con la potencia, se cancelan, por las propiedades de la potenciación.”
Es claro cómo el docente explica el proceso aritmético de las potencias de i, utilizando las propiedades de la potenciación y a su vez, hablando de raíces de radicando negativo. Es mediante estos argumentos que fue necesario organizar las categorías metafóricas que el docente empleó en su discurso, pues permitió identificar con mayor claridad las raíces de las metáforas conceptuales que se pretendía analizar.
A través de esta categorización, se realizó la codificación abierta de todas las expresiones metafóricas encontradas en las transcripciones de cada profesor, construyendo de esta forma el corpus de metáforas en donde se hizo la respectiva clasificación de expresiones metafóricas, según las metáforas conceptuales referidas en el marco teórico. En dichas codificaciones, es evidente cómo el discurso está permeado constantemente por metáforas conceptuales, de las cuales se escogieron 12 para el profesor 1 y 14 para el profesor 2, con el fin de elaborar las entrevistas para estudiantes y docentes y, posteriormente, realizar el análisis de variables y así determinar la incidencia de dichas expresiones metafóricas en el aprendizaje del concepto de número complejo.
B. Variables estudiadas
En la investigación se buscó determinar la incidencia del lenguaje metafórico empleado por el docente en el aprendizaje del número complejo, teniendo como punto referente la teoría del análisis del contenido mediante las entrevistas estructuradas por el investigador. Con dichas entrevistas, se realizó una comparación entre las respuestas de cada estudiante a la pregunta por la comprensión de lo que expresó el docente a través de las expresiones metafóricas, y el significado pretendido por el docente, para determinar un grado de coincidencia en las respuestas. Para la medición de dicha coincidencia se utilizó la escala tipo Likert. Este método fue desarrollado por Rensis Likert en 1932; sin embargo, según [14], se trata de un enfoque vigente y bastante popularizado. El método consiste en calificar de manera numérica una serie de ítems presentados en una encuesta con el fin de medir la variable de estudio.
De esta manera, si la respuesta de la estudiante fue muy acorde con lo pretendido por el docente, esta obtuvo una calificación de 5; si por el contrario, lo expresado por la estudiante no coincidía en nada con lo pretendido por el docente, la calificación que obtuvo fue de 1, y así sucesivamente, según la Tabla I.
En el caso de esta investigación, en primera medida se analizó la variable coincidencia entre respuestas, seguido de la variable coincidencia entre intencionalidad del docente y la definición formal matemática; finalmente, se realizó un contraste entre ambas coincidencias para determinar el tipo de incidencia. Para ello, se le entregó el cuestionario a cada estudiante, con el propósito de indagar por la comprensión de algunas expresiones metafóricas utilizadas en la clase por el profesor. De igual manera, a cada docente se le entregó una entrevista que indagaba acerca de la intencionalidad al referirse a cierta expresión metafórica durante la clase. Esta información se condensó en una tabla para evidenciar la medición de la coincidencia entre la comprensión del estudiante ante la metáfora y la intención del docente al referirse a ella, calificando dicha coincidencia con la escala Likert.
IV. RESULTADOS
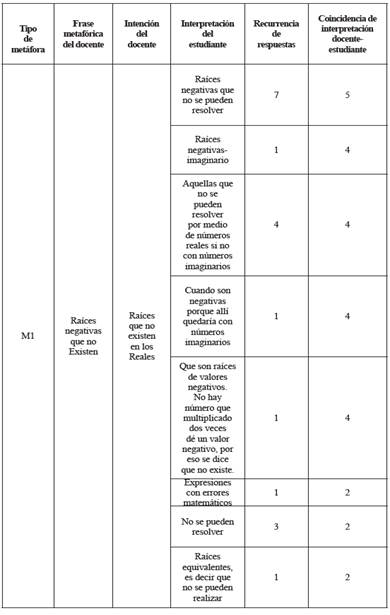
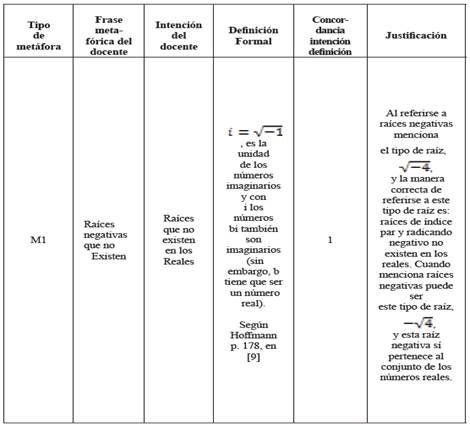
Los resultados se consignaron en una tabla como la que se muestra en la Tabla II para el caso de la metáfora 1 (M1), en la cual se puede apreciar el grado de coincidencia según la escala Likert entre la intención del docente con la frase metafórica M1 y lo que los estudiantes comprendieron de dicha frase.
Se calificó cada una de las metáforas del cuestionario para ambos docentes. Luego, se construyó la tabla donde se calificó la coincidencia entre la intencionalidad del docente y la definición formal de un libro de matemáticas. Los resultados de esta comparación se consignaron en la Tabla III.
TABLA III Calificación de coincidencia entre intencionalidad y definición formal para la metáfora 1 del profesor 1
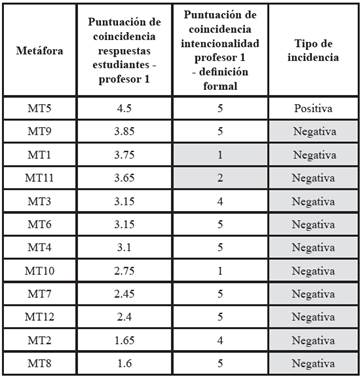
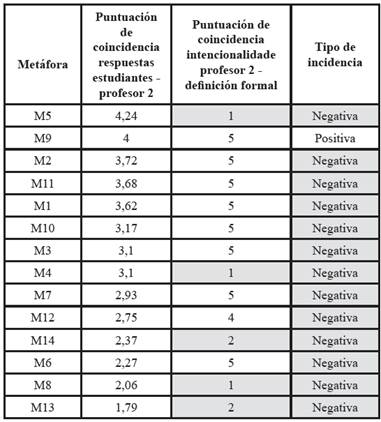
Teniendo la calificación de la variable coincidencia para cada metáfora, se realizó el contraste entre ambos resultados para determinar el tipo de incidencia de las metáforas identificadas en el discurso de cada profesor. Dicho contraste se efectuó mediante la construcción de una tabla en la cual, si la coincidencia entre respuestas es alta y la coincidencia entre intencionalidad y definición formal es alta, se considera que la incidencia es positiva; pero, si la coincidencia entre respuestas es baja y la coincidencia entre intencionalidad y definición formal es alta, la incidencia es negativa y viceversa, lo que se indica con el sombreado. Los resultados del contraste de variables realizado se muestran en la Tabla IV, para el profesor 1 y en la Tabla V para el profesor 2.
Tanto en la Tabla IV como en la Tabla V, se puede apreciar una incidencia negativa casi en la totalidad de los casos. Esto permite ver, para el caso de estos dos profesores y con el tema del concepto de número complejo que, aunque en las entrevistas ellos consideraban hacer bien su trabajo, el concepto no fue comprendido por la mayoría de estudiantes.
Un hecho bastante llamativo en el análisis del discurso de cada profesor, concierne a su formación académica: a pesar de que un profesor es licenciado en Matemáticas y Física de la UTP y el otro Tecnólogo mecánico de la UTP, ambos presentaron un nivel de incidencia negativo muy alto con respecto a las expresiones metafóricas analizadas. Los resultados muestran que su intencionalidad con la expresión metafórica, la mayoría de las veces coincide con la definición formal, lo que implica que ambos presenten una coincidencia satisfactoria entre su intencionalidad y la definición formal. Lo que no sucede con la coincidencia entre las respuestas de los profesores y las de sus estudiantes, ya que para el análisis de dicha variable ambos profesores presentaron niveles muy bajos.
V. CONCLUSIONES
De los resultados del análisis de los discursos de aula de los dos profesores enseñando el concepto de número complejo, se puede concluir que:
Fue posible corroborar que en el discurso de los profesores que participaron en el estudio hay presencia de metáforas como recurso cognitivo, una presencia no consciente y que es una manifestación, como asegura [12], del imaginario social, del que habla Castoriadis en [2], de los profesores de matemáticas en el Eje Cafetero.
También se pudo corroborar el hecho de que los contenidos de las matemáticas no son ajenos a las manifestaciones culturales en las cuales se encuentran inmersos los profesores, como agentes que aseguran la continuidad de un conocimiento que se inició en un tiempo y un espacio lejano a los estudiantes en la región del Eje Cafetero donde se intentan enseñar, algo que ya [5] había sugerido cuando hablaba de la Etnomatemática en grupos humanos diferenciados por sus prácticas sociales y culturales.
Los dos profesores en la mayoría de los casos muestran un manejo de los conceptos. Sin embargo, al usar lenguaje metafórico para explicar dichos conceptos confunden al estudiante y no logran generar el aprendizaje del concepto de número complejo.
Se logró evidenciar en la entrevista realizada a ambos profesores cómo cada uno, al especificar el significado pretendido con la expresión metafórica, manifestaba no recordar haber dicho eso; esto como registro del grado de inconsciencia con el cual el profesor utilizó la expresión en su clase. Las metáforas analizadas surgen en su gran mayoría, cuando las estudiantes le manifiestan al profesor no entender lo que él ha dicho; de allí, el profesor recurrió a un lenguaje menos formal y más metafórico para hacerse entender, lenguaje que, según los resultados obtenidos en la investigación, obstaculizó en la mayoría de los casos el proceso de aprendizaje del concepto de número complejo.
Se observa que, en algunos casos, como el de la metáfora 5 (M5), usada por el profesor 2, la coincidencia con las respuestas de los estudiantes es alta, sin embargo, la coincidencia entre la intencionalidad del profesor y la definición formal es baja, debido a que la forma como lo conceptualiza el profesor es errada. Esto ocasiona una reproducción del error, ya que el estudiante comprendió lo que el docente quiso decir con la expresión, pero interiorizó mal un significado desde la definición matemática formal, así, esta metáfora obstaculizó el aprendizaje de los estudiantes. Por consiguiente, si no se tiene consciencia de la expresión metafórica que se va a utilizar para la explicación en clase, y se utilizan expresiones metafóricas improvisadas, esto puede generar un aprendizaje errado de un concepto, el cual va a obstaculizar el aprendizaje de otros derivados del concepto que se está tratando de enseñar.
Se evidencia de los resultados que muy pocos estudiantes comprendieron las expresiones utilizadas por el docente en clase, cuestión que resulta común en el aprendizaje de las matemáticas, con el hecho de ser siempre la minoría quienes ganan y muchos quienes pierden. Con esto, se acostumbra a pensar en las dificultades que tiene el estudiante para comprender las matemáticas y no en las dificultades que pueden ser generadas por el docente. La investigación evidencia las dificultades que se presentan en el proceso de comunicación y los resultados sustentan aún más las teorías referidas en el marco teórico; las metáforas, al ser pensadas y concebidas desde la experiencia de cada persona pueden no ser comprensibles para todos, convirtiéndose en un problema para lograr el aprendizaje de las matemáticas. En el caso del que trata esta investigación, las metáforas analizadas incidieron negativamente en la comprensión del concepto de número complejo. Se concluye que, aunque la metáfora permea directamente nuestro sistema conceptual, esta deber ser pensada bajo una intencionalidad mediada con el estudiante para concretar significados en el desarrollo de la clase.
De los resultados de las entrevistas a los estudiantes se desprende que para una misma frase metafórica empleada por el profesor se presentan diferentes interpretaciones, casi que una diferente por cada estudiante; unas que concuerdan en características y otras que evidencian confusión en la comprensión. De este hecho se ratifica la existencia de un sistema conceptual permeado constantemente de metáforas construidas desde la experiencia de cada persona. Al buscar conceptos matemáticos en el lenguaje de las personas, es necesario buscar unanimidad al referirse a un término matemático que está matizado por una expresión metafórica, de lo contrario, cada estudiante en el aula comprenderá lo que le sea posible según sus vivencias. En este orden de ideas, la utilización de lenguaje metafórico para explicar conceptos matemáticos no puede ser utilizado de manera improvisada por el docente, sino que debe ser concertado, analizado, pensado y compartido antes del desarrollo de la clase, contrastado en la institucionalidad del concepto, como sugiere [1], con el fin de alcanzar un buen proceso de comunicación en la enseñanza de las matemáticas.
Generalmente no se da una conexión estrecha entre el lenguaje concebido por un profesional de la enseñanza de las matemáticas (profesor) con un estudiante que inicia su experiencia en esta ciencia, lo cual genera un conflicto de significados que deben ser mediados, precisamente en el proceso comunicativo; a esto se le suman los demás problemas de aprendizaje que se presentan habitualmente en el aula. Como advierten [10], el mundo como lo percibimos y la forma como nos movemos en él está estructurado por los conceptos que manejamos, es más, se podría decir que el sistema conceptual define nuestra realidad. Asimismo, sucede con el conocimiento matemático, es una construcción de realidades que se da gradualmente y en la cual todos participan. Por tanto, el proceso de comunicación que media dicha construcción debe contar con un lenguaje comprensible para todos.