I. INTRODUCCIÓN
La CG (Computacional Geometry) puede entenderse como una disciplina que se ocupa del análisis y diseño de algoritmos computacionales para resolver problemas en el ámbito geométrico [1], [2]. Muchos de estos algoritmos utilizan como base una cadena poligonal convexa comúnmente denominada CH (Convex Hull). Típicamente, el CH es considerado como un importante problema computacional y se refiere a la construcción de polígono convexo que constituye la envoltura más externa de un conjunto de puntos dado [2].
Realizar la implementación de algoritmos para obtener una cadena poligonal correspondiente al CH, es un cálculo computacional con diversas aplicaciones como son la planificación de rutas evitando colisiones (por ejemplo en robots o vehículos autónomos [3], [4]) y el reconocimiento de patrones en gráficos (por ejemplo en la visión por computador [5]). En este sentido, el presente trabajo implementó los algoritmos QuickHull, Gift Wrapping y Graham Scan que calculan el CH incorporando modificaciones para reducir el tiempo de ejecución, lo anterior, enmarcados en la investigación base que contempla entre otros aspectos reducir la latencia en el intercambio de mensajes entre microservicios [6].
El contenido adicional de este trabajo consta de las siguientes cinco secciones: II. Trabajo relacionado, III. Marco teórico, IV. Metodología, V. Resultados y Análisis y VI. Conclusiones.
II. Trabajo relacionado
Esta sección presenta cronológicamente algunos estudios relacionados con la presente investigación.
Sunday en su trabajo del 2006 denominado “The Convex Hull of a 2D Point Set or Polygon” [7], presenta una revisión general de diferentes algoritmos para el cálculo del CH.
Para 2009, Qiha en la publicación denominada “New serial and parallel algorithms for finding convex hull based on clusters, domains and directions from single to multitude” [8], presenta un teorema fundamental isomórfico a partir del cual propone dos algoritmos (uno serial y otro paralelo) para encontrar el CH.
Chiang en su trabajo del 2010 titulado “Solving 2D Convex Hull With Parallel Algorithms” [9], presenta una implementación de un algoritmo divide y vencerás que calcula el CH usando paralelismo mediante el aprovechamiento de CPU y GPU.
En 2015, Hoang y Linh en su trabajo “Quicker than Quickhull” [10], proponen una variación del algoritmo QuickHull denominado QuickerHull; el cual incluye mejoras para reducir el tiempo de ejecución del algoritmo.
Skala et al. en su trabajo de 2016 llamado “Reducing the number of points on the convex hull calculation using the polar space subdivision in E2” [11], presentan un método basado en una subdivisión del espacio polar para reducir el conjunto de puntos de un polígono dado, con el fin de acelerar los algoritmos para el cálculo del CH.
En 2018, Gamby y Katajainen realizaron implementaciones de los algoritmos Plane-Sweep, Torch, QuickHull y Throw-Away para evaluar su eficiencia, los resultados fueron publicados en “Convex-Hull Algorithms: Implementation, Testing, and Experimentation” [12]. En 2019, estos mismos autores, en su trabajo “A Faster Convex-Hull Algorithm via Bucketing” [13], propusieron una variante del algoritmo Via Bucketing, logrando una mejora en su tiempo de ejecución.
Borna en su publicación de 2019 titulada “Sweep Line Algorithm for Convex Hull Revisited” [14], presenta un nuevo algoritmo para el cálculo del CH denominado Sweep Line, logrando un tiempo de ejecución en el orden de O(nlogn).
Finalmente, Lesjak en 2021 con su trabajo “Pregled in primerjava algoritmov za izračun konveksne ovojnice” [15] presenta una revisión de algoritmos clásicos y modernos para el cálculo del CH. En el trabajo se destaca el algoritmo Ordered Hull siendo más rápido que el Quickhull.
III. MARCO TEÓRICO
Esta sección contiene aspectos teóricos relevantes para la comprensión del tema tratado en este trabajo.
A. Geometría computacional
La CG es un campo de la informática que comenzó en los años 70s y según Forrest, citado por [16] está relacionada con la representación computarizada, análisis, síntesis (diseño) y manufactura controlada por computadora de formas bidimensionales y tridimensionales. En otras palabras, la CG puede entenderse como una disciplina que se ocupa del análisis y diseño de algoritmos computacionales para resolver problemas en el ámbito geométrico. La CG ha tenido una fuerte interacción con diversos campos de ciencia e ingeniería como Algoritmos, Estructuras de Datos, Matemáticas, Geometría Euclidiana, Optimización, entre otros [17]. Desde la década de los 90s existe una demanda de la CG en una variedad de áreas de las ciencias aplicadas tales como Sistemas de Información Geográfica, Visualización, Robótica y Gráficos por Computadora; estas áreas han propiciado aún más la investigación en CG [17].
1) Términos básicos
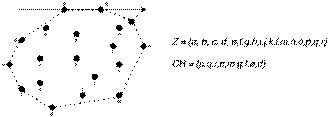
Punto: Es considerado el elemento geométrico más sencillo. Definido como un conjunto de números reales ya sean en dos [x,y] o tres [x,y,z] dimensiones. En laFig. 1, un punto es cualquier de los elementos del conjunto Z.
Segmento: Se define a partir de dos puntos [ punto 1 , punto 2 ]; si se llega a considerar la orientación del segmento se le considera un vector. En laFig. 1se muestra un segmento conformado por los puntos pq.
Polígono: Se denomina polígono a una superficie plana cuyo borde está formado por segmentos rectos. En laFig. 1se muestra el polígono CH.
Cadena poligonal: Un conjunto ordenado de puntos distintos en el plano determina una cadena poligonal, que es la unión de los segmentos. CH de en laFig. 1, también representa una cadena poligonal.
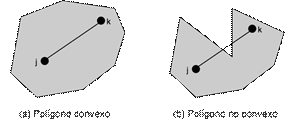
Convexidad: El concepto de convexidad puede definirse así: un conjunto S del plano se considera convexo si j Î S y k Î S, lo que implica que el segmento jk Í S [18] , [19] , verFig. 2.
2) Cálculo del Convex Hull
Es importante reconocer que el CH de un conjunto Z (conjunto de puntos en el plano), es un polígono convexo que contiene a Z [18]. Yendo más allá, y basados en la Fig. 1, al identificar un borde del CH del polígono Z conformado por los puntos pq notamos que ambos son puntos de Z y que al trazar una línea a través de estos puntos (teniendo en cuenta para la orientación el sentido de las manecillas del reloj) obtendremos que los demás puntos de Z se encuentran a la derecha. Esta es la idea que abarca el aspecto geométrico del problema relacionado con el cálculo del CH.
Existen diversos algoritmos para calcular el CH siendo algunos de los más destacados los siguientes: QuickHull, Gift Wrapping y Graham Scan. A continuación, se presenta el pseudocódigo de cada uno de ellos.
a) Algoritmo QuickHull
Este algoritmo fue sugerido por diversos investigadores a finales de los 70s [20], [21], y fue llamado QuickHull por Preparata y Shamos en 1985 [16], citado por [19], [22] y [23]. La complejidad del QuickHull según [20] es del orden O(nh), siendo n el número de puntos y h el número de vértices del CH. Ver Fig. 3.
b) Algoritmo Gift Wrapping
Este algoritmo fu propuesto por Chand y Kapur en 1970 [24] y tiene una complejidad del orden O(nh), siendo n el número de puntos y h el número de vértices del CH. Ver Fig. 4.
c) Algoritmo Graham Scan
Este algoritmo hereda el nombre del apellido de su autor Ronald Graham, quien lo propuso en 1972 [25]. Este algoritmo tiene una complejidad del orden O(nlogn), siendo n el número de puntos. Ver Fig. 5.
IV. METODOLOGÍA
El proceso metodológico seguido en este trabajo consistió en la implementación de los siguientes pasos:
A. Paso No 1 - Implementación de los algoritmos
Se implementó en lenguaje de programación JAVA algoritmos para el cálculo del CH. Además, se construyeron versiones alternativas a los algoritmos buscando mejorar los tiempos de ejecución.
B. Paso No 2 - Generación de los datos de prueba
En este paso se generaron veinte archivos, cada uno con un conjunto de puntos aleatorios, cuyos valores coordenadas (x,y) están entre -10.000 y 10.000. En la generación de los puntos se usaron algoritmos con una distribución uniforme, lo anterior para que todos los números entre -10000 y 10000 tuvieran la misma probabilidad de ocurrencia. Por ejemplo, si se generan 20.000 valores aleatorios, debería esperarse que cada valor se genere aproximadamente 1 vez en promedio. Sin embargo, debido a la naturaleza aleatoria de la función empleada, el número real de veces que se genera cada valor puede variar ligeramente. En este caso, la probabilidad de que se genere un número determinado es de 1/20001, porque hay 20001 valores posibles en el intervalo (de -10000 a 10000, ambos inclusive). El número de puntos de cada uno de los archivos varia así: 5.000, 10.000, 15.000, 20.000, 25.000, 30.000, 35.000, 40.000, 45.000, 50.000, 55.000, 60.000, 65.000, 70.000, 75.000, 80.000, 85.000, 90.000, 95.000 y 10.000.
C. Paso No 3 - Ejecución de los algoritmos
Se ejecutó los algoritmos en un computador portátil con procesador Core i7 de 4 núcleos a 2.3 GHz, 16 Gigas de memoria RAM DDR3 a 1600 MHz, unidad de estado sólido WDC WDS100T2B0A y tarjetas de video Intel HD Graphics 40000 y NVIDIA GeForce GT 650M. Para la ejecución de cada uno de los algoritmos se usó como parámetro de entrada cada uno de los veinte archivos generados. Cómo estrategia para disminuir el ruido generado por otros procesos ejecutados en el computador, cada uno de los archivos se procesa con cada uno de los algoritmos 100 veces; esto permitió tomar los tiempos para cada algoritmo al calcular el CH para los puntos dados.
V. RESULTADOS Y ANÁLISIS
A continuación, se presentan los resultados de la implementación y ejecución de los algoritmos QuickHull, Gift Wrapping y Graham Scan.
A. Implementación del QuickHull
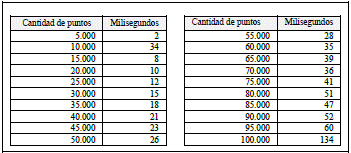
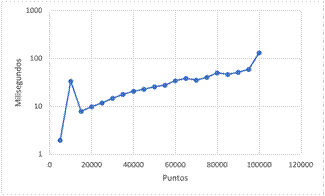
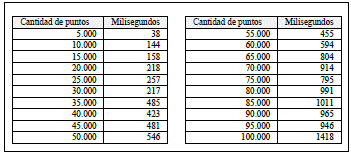
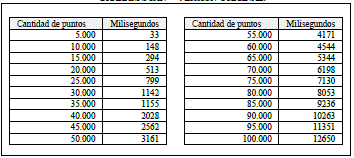
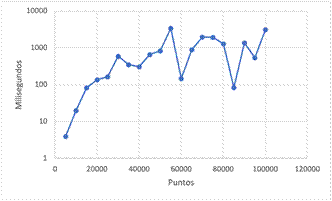
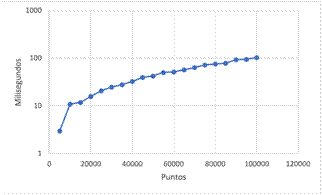
La Tabla I muestra los resultados obtenidos al ejecutar este algoritmo con diferentes conjuntos de puntos. Además, en la imagen Fig. 6 se puede observar un comportamiento coherente de los tiempos de ejecución con relación a la complejidad del algoritmo. Sin embargo, al inicio y fin del gráfico, se observan datos atípicos que pueden deberse a la falta de asepsia computacional.
B. Implementación del Gift Wrapping
Durante la implementación del algoritmo Gift Wrapping, se construyeron dos versiones, una original y otra modificada.
1) Gift Wrapping - Versión Original
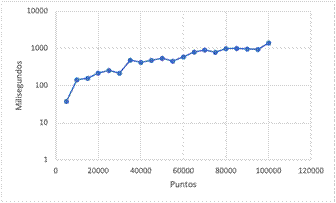
Implementación original del algoritmo Gift Wrapping descrito en el trabajo [24] (ver Fig. 4). La tabla II muestra los tiempos obtenidos al ejecutar el algoritmo. Además, en la Fig. 7 se muestra el comportamiento del algoritmo, que es consistente a su complejidad.
C. Gift Wrapping - Versión Modificada
Esta implementación corresponde a una versión modificada del algoritmo Gift Wrapping original y continúa teniendo la misma complejidad O(nh).
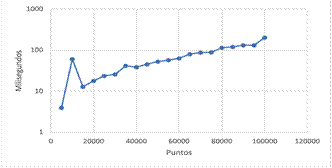
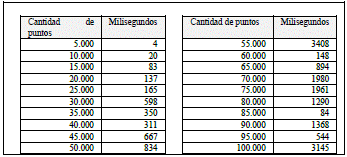
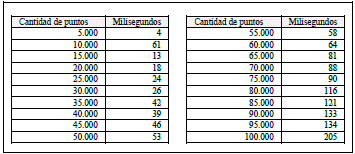
La tabla III muestra una reducción significativa en los tiempos de ejecución en comparación con los datos del algoritmo original (ver tabla II). Esta reducción en los tiempos de ejecución está relacionada con la estrategia usada para comparar los ángulos formados por los vértices. Además, en la Fig. 8 se muestra el comportamiento del algoritmo Gift Wrapping - Versión modificada. Sin embargo, al inicio del gráfico, se observa un valor atípico que pueden deberse a la falta de asepsia computacional.
TABLA III TIEMPOS DE EJECUCIÓN OBTENIDOS AL EJECUTAR EL ALGORITMO GIFT WRAPPING - VERSIÓN MODIFICADA.
D. Comparación entre implementaciones del algoritmo Gif Wrapping
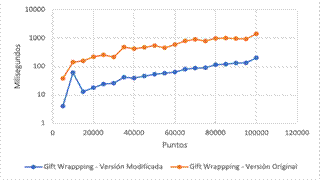
En la Fig. 9 se muestra en una comparación entre las implementaciones del algoritmo Gift Wrapping. Como se puede observar, la versión modificada es más rápida que la versión original. La diferencia entre estas versiones radica en la estrategia usada en la comparación de los ángulos entre vértices, se puede inferir que la estrategia usada en el algoritmo modificado es efectiva, toda vez que evita realizar cálculos en la comparación de ángulos y en consecuencia se presenta una disminución en los tiempos de ejecución. La estrategia usada para comparar los ángulos en la versión original emplea la función del API de JAVA para calcular ángulos y así determinar cuál es el menor. Por otra parte, la estrategia usada por la versión modificada emplea la orientación de puntos para determinar cuál es el ángulo menor.
E. Implementación del Graham Scan
Durante la implementación del algoritmo Graham Scan, se construyeron tres versiones, que incluyen la versión original (ver Fig. 5) y dos versiones modificadas.
1) Graham Scan - Versión Original
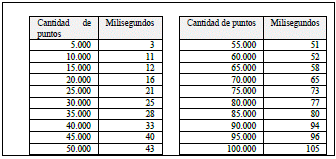
Implementación original del algoritmo Graham Scan descrito en el trabajo [25] (ver Fig. 5). La tabla IV muestra los tiempos obtenidos al ejecutar el algoritmo. Además, en la Fig. 10 se muestra el comportamiento del algoritmo, que es consistente a su complejidad.
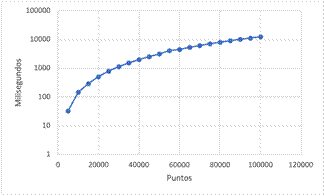
Fig. 10 Comportamiento del algoritmo Graham Scan - Versión Original y basado en los datos de la tabla IV.
2) Graham Scan - Versión Modificada Nº 1
Esta versión incorpora un proceso previo de eliminación de vértices, el cual consiste en encontrar los puntos extremos de la nube de puntos, para formar con ellos un rombo y remover de la nube de puntos todos aquellos que se encuentran al interior del rombo. Esta versión mantiene la complejidad original del algoritmo. Sin embargo, puede reducir drásticamente los tiempos de ejecución dependiendo de la cantidad de puntos que se remuevan al inicio.
La tabla V muestra una reducción significativa en los tiempos de ejecución en comparación con los datos del algoritmo original (ver tabla IV). Además, en la Fig. 11 se muestra el comportamiento del algoritmo Graham Scan - Versión Modificada Nº 1, que describe un comportamiento irregular. Esta situación está relacionada con la cantidad de puntos que logran eliminarse a través de la estrategia de reducción aplicada al inicio del algoritmo y la cual varía según la dispersión existente en la nube de puntos.
3) Graham Scan - Versión Modificada Nº 2
Esta versión incorpora un proceso previo de eliminación de vértices, el cual consiste en encontrar los puntos extremos de la nube de puntos, para formar con ellos un octágono y remover de la nube de puntos todos aquellos que se encuentran al interior. Esta versión mantiene la complejidad original del algoritmo. Sin embargo, puede reducir drásticamente los tiempos de ejecución dependiendo de la cantidad de puntos que se remuevan al inicio.
La tabla VI muestra una reducción significativa en los tiempos de ejecución en comparación con los datos del algoritmo original (ver tabla IV). Además, en la Fig. 12 se muestra el comportamiento del algoritmo Graham Scan en la versión modificada Nº 2 donde se evidencia que los tiempos de ejecución empleados indican una evidente optimización para el conjunto de puntos considerados en la investigación.
4) Comparación entre implementaciones del algoritmo Graham Scan
En la Fig. 13 se muestra una comparación entre la implementación original del algoritmo Graham Scan y dos versiones modificadas. Se puede notar que las dos versiones modificadas presentan menor tiempo de ejecución que la versión original, siendo la versión modificada Nº 2 la más rápida. Aunque las versiones modificadas usan en general estrategias de reducción de puntos, la implementación da versión modificada Nº 2 demuestra ser más eficientes al lograr la eliminación de más puntos.
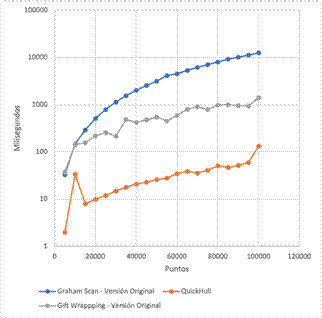
Fig. 13 Comparación del comportamiento entre implementaciones de los algoritmos originales QuickHull, Gift Wrapping y Graham Scan.
5) Comparación de algoritmos QuickHull, Gift Wrapping y Graham Scan
A continuación, se presentan comparaciones entre los algoritmos QuickHull, Gift Wrapping y Graham Scan en sus versiones originales (Ver Fig. 13). También se muestra el resultado de la comparación entre la implementación del algoritmo QuickHull y las versiones más rápidas de las implementaciones de los algoritmos Gift Wrapping y Graham Scan (ver Fig. 14).
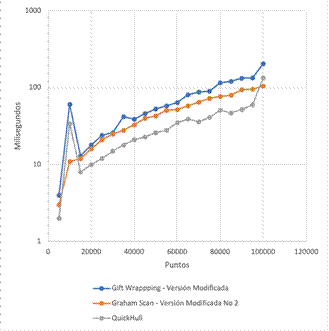
Fig. 14 Comparación del comportamiento entre implementaciones de los algoritmos QuickHull y las versiones modificadas de Gift Wrapping y Graham Scan.
En la Fig. 13 se puede evidenciar que el QuickHull es el más rápido, marcando una notable diferencia con respecto a los tiempos de ejecución de los demás algoritmos.
Por otro lado, la Fig. 14 evidencia que el QuickHull sigue siendo el algoritmo más rápido, sin embargo, también se nota que la diferencia respecto a los tiempos de ejecución de los demás algoritmos se ha reducido significativamente. Esta reducción es debido a la inclusión de las modificaciones en los algoritmos Gif Wrapping y Graham Scan.
Considerando los tiempos observados para la ejecución de los algoritmos Gift Wrapping y QuickHull durante el procesamiento del archivo con los 100 mil puntos. Esta situación puede haber sido influenciada por una distribución también atípica en los puntos, donde los algoritmos QuickHull y la versión modificada del Gift Wrapping fueron ligeramente más lento que la versión modificada del Graham Scan.
VI. CONCLUSIONES
Se implementaron los algoritmos QuickHull, Gift Wrapping y Graham Scan para el cálculo del CH, usando 20 archivos. Cada archivo incluía una nube de puntos aleatoria. Los archivos generados tenían tamaños que iban desde los 5.000 puntos hasta los 100.000 puntos.
Para los algoritmos Gift Wrapping y Graham Scan se realizaron implementaciones modificadas con la intención de reducir los tiempos de ejecución. Con respecto a la implementación modificada del algoritmo Gift Wrapping, se tomó como estrategia comparar los ángulos formados por los vértices, lo que condujo a significativa reducción en el tiempo de ejecución frente a la versión original de este algoritmo. Para el algoritmo Graham Scan se realizaron dos implementaciones modificadas que emplearon como estrategia reducir el tamaño de la nube de puntos.
A partir de la comparación entre las todas las implementaciones realizadas en la investigación, se comprobó que el algoritmo QuickHull es el más rápido. También se nota reducción en los tiempos de ejecución en las implementaciones modificadas con relación a las implementaciones originales de los algoritmos Gift Wrapping y Graham Scan.
Como trabajo futuro, se podrán realizar implementaciones y comparación con otros algoritmos que calculan el CH buscando optimización en el tiempo de ejecución. Adicionalmente, se podrá usar el polígono convexo CH como una base para encontrar la ruta en la arquitectura de los microservicios que permita la reducir la latencia. También, se podrá realizar la construcción de una herramienta software para apoyar el proceso de enseñanza-aprendizaje del CH, permitiendo una fácil evaluación de implementaciones algorítmicas para calcularlo.