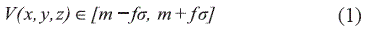Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Ingeniería Biomédica
Print version ISSN 1909-9762
Rev. ing. biomed. vol.1 no.2 Medellín July/Dec. 2007
FAST AND ACCURATE COMPUTATION OF THE EUCLIDEAN DISTANCE TRANSFORM IN MEDICAL IMAGING ANALYSIS SOFTWARE
Cristina Gallego Ortíz
Biomedical Engineering Program. Escuela de Ingeniería de Antioquia-Universidad CES. bmcriga@eia.edu.co.
Received August 14, 2007. Accepted November 18, 2007.
ABSTRACT
Fast and accurate computation of the Euclidean distance map transformation is presented using the python programming language in conjunction with the vtk and itk toolkits. Two algorithms are compared on the basis of their efficiency and computational speed; Saitho algorithm and Danielsson's four-points Sequential Euclidean Distance (4SED). An algorithm is used to compute a scalar distance map from a 3D data set or volume, which can be used to extract specific distance values. The performance time for the Saitho computation speed was less than the Danielsson's 4SED computation allowing a faster calculation of the Euclidean distance map. A software analysis application was implemented using the Saitho algorithm for the computation of the scalar distance maps; it also included an underlying segmentation method to allow the computation of Euclidean distance maps on micro-CT images of segmented bone structures. In the future, this application could be used in conjunction with other image processing software applications of bone analysis.
KEY WORDS: Euclidean distance map, Euclidean distance transformation, Image segmentation.
RESUMEN
Se implementó una aplicación utilizando el lenguaje de programación Phyton y las librerías ITK y VTK para un cálculo rápido y preciso de la transformada Euclidiana de distancia. Se compararon dos algoritmos, el propuesto por Saitho y el algoritmo de Danielsson en la versión four-points Sequencial Euclidean distance (4SED). Se evaluó la precisión y la velocidad computacional de ambos algoritmos, encontrando que la versión propuesta por Saitho es más rápida. Se implementó una aplicación de software para el cálculo de la transformada Euclidiana de distancia, incluyendo herramientas para la segmentacion de imágenes de micro-CT de estructuras óseas. A futuro esta aplicación puede ser usada en conjunto con otros software para análisis de imágenes en el procesamiento de estructuras oseas.
PALABRAS CLAVE: Mapa de transformada de distancia, Transformada de distancia Euclidiana, Segmentación de imágenes.
I. INTRODUCTION
Distance transformations are powerful image analysis tools able to map on a volume dataset, in the case of the Euclidean distance transform (EDT), a distance map that contains the closest distance of a pixel on an object of interest to any pixel in the background or in the case of the signed EDT, the closest distance of any voxel to a voxel or sets of voxels of interest [1].
Distance transformed computations have a vast area of application within medical imaging processing, especially for registration in orthopedic surgery and biomechanical studies of joints [2-4]. Current in vitro and clinical intervention studies reveal little information on potential modifications of soft tissue due to injury or disease. This is being overcome by novel techniques that use computation of distance maps on in vivo bone modeling and noninvasive studies of articulations using computed tomography (CT).
In the field of colon endoscopy, current methods for computation of the centerline of a colon from Computed Tomographic Colonography (CTC) are time-consuming and tedious [5]. This is due to the fact that current techniques depend on the successful tracking of a navigation system through the colon. To overcome this difficulty, the center line computation of the colonic lumen is calculated extracting local maxima in a distance map of the segmented colon lumen, and then local maxima is used to compare and link connection criteria from the Euclidean distance between maximums, as shown in previous studies [5].
Application of distance transform computation in the area of pattern recognition [6] and artificial intelligence systems [7] have been proposed in the past. A Kohonen neural network is trained using typical features of the subclasses in a learning set by means of a shortest Euclidean distance algorithm. The study describes the use of a Kohonen map in the classification of renal diseases as being glomerular or tubular aiming to assist nephrological decision-making.
New promising fields of applications of distance transformations have emerged from results of previous studies, as in the case of an intra-operative navigational guidance for computer-integrated orthopedic surgery [4]. In this context, the algorithm used to compute the distance transformation has to provide reasonable calculation time without loss of accuracy in the distance calculation. To reach this objective, several strategies for the computation of distance maps are used. The first strategy is to use local transformations, which assume that the corresponding distance value of a pixel can be deduced from the values of its neighbors. But this is not exactly true for the computation of the Euclidean distance transform so that these methods lead only to approximations of the exact transformation. This is the case of Danielsson's four-point Sequential Euclidean Distance mapping or 4SED algorithm, which falls in this category of approximate algorithms [2].
For the computation of the exact Euclidean transform, other methods are necessary. The existing algorithms can be basically classified in three categories. Parallel and sequential propagation, raster-scanning and contour-processing algorithms [2]. Raster-scanning algorithms and propagation methods are used by the Saitho algorithm. This algorithm has been proven to be the fastest exact Euclidean distance transform for general purpose computers, although its computational cost is highly image dependent and its complexity can reach n3 for n x n images [8].
A Graphical User Interface (GUI) was developed that implements the Saitho algorithm for the computation of Euclidean distance scalar maps, using the unsigned version of the Saitho algorithm, with the python programming language and the VTKVTKVTK and ITKTK toolkits. The software application allows the user to manage SunVision volume file format (vff) datasets, to segment bone structures from micro-CT mice images using thresholding with global and local voxel criteria, and region-growing techniques based on manually selected seed. This is an approach to a possible application of image analysis software for the computation of euclidean distance maps of binary images of segmented mouse bone structures in micro-CT datasets.
II. MATERIALS AND METHODS
Materials
Datasets with isotropic voxel spacing of 1.0 mm and 0.154 mm, and medium sized datasets with voxel dimensions ranging from 2003 to 4003 were used. SunVision volume file format (vff) micro-CT datasets of mouse were used to test bone segmentation tools of the application.
Synthetic vffs volume datasets were also used, consisting on binary objects of different geometries as a cube, a sphere and a cylinder-sphere as a more complicated structure.
Methods
A. Segmentation
Segmentation tools provide the user with a multi-step approach for segmentation of bone tissue from other soft tissue. The main reason for including a segmentation tool in the GUI is because the authors are interested in the approach to the computation of Euclidean distances maps of segmented mouse bone structures of micro-CT datasets. Current methods involve the use of global and local thresholding criteria as a previous step before the region or seed-growing algorithm is applied to a CT volume dataset for bone segmentation [9, 10].
We have selected a three steps segmentation method that uses a mixture of global and local criteria for the computation of the region-growing algorithm. Our method can be understood as follows: the user, based on commonly CT values that are labeled as bone, selects the first global threshold, setting up the voxel value of those pixels to be segmented, that we called the "black in" voxel value, so that a first version of the binary output image is obtained. Then, the region-growing algorithm is computed using local statistics on the 26-voxel-neighborhood region. The selection of seeds is based on intensity values of voxels that are bone but that were not segmented using the first step of global thresholding. The region-growing algorithm includes those voxels V(x, y, z) whose intensities are inside the interval:
Where m is the mean and σ is the standard deviation of the intensity levels found in the neighborhood region of the voxel seeds, and f is a factor of inclusion voxel criteria.
A final step of the segmentation is based on the addition of multiple seeds, to allow the algorithm to select voxels from other regions that have not been included in the first iteration of the region growing step.
B. Computation of the Euclidean distance transform
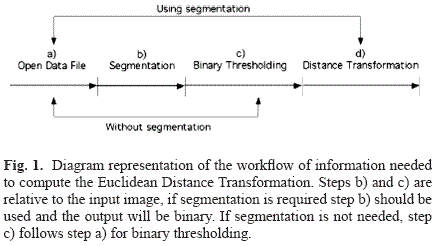
The computation of the distance transform is organized into several modules, which separate the pre-processing, segmenting and binary thresholding stages. The output of a stage is intended to be the input of the next stage, which gives the user the possibility to integrate all techniques necessary for the computation of the distance map, since the input datasets should be binary datasets.
A segmentation tool was developed using global and local thresholding and region growing techniques, as a necessary pre-processing stage to apply the distance transformation to segmented-bone CT datasets.
The computation is done over a binary image were the convention is to differentiate voxels as being target voxels and background voxels. A diagram representing the main steps necessary for the computation of the Euclidean distance is shown in Fig. 1.
C. Comparison of Saitho and Danielsson (4SED) algorithms
For the comparison of Saitho and Danielsson (4SED) algorithms, two types of tests were performed: accuracy and computational time tests. The accuracy test consisted on matching an extracted iso-distance from each distance map. Using the synthetic vffs volume datasets, these iso-distances were extracted and compared using specificity and sensibility tests in relation to a countour of an object of the same size of the evaluated iso-distance. The computational time test took into consideration the period of time spent for each algorithm to perform a given task.
The reason for this is to compare the accuracy of both versions of the distance transform when performing the task of computing a fixed distance. This iso-distance is then converted to a binary contour to be compared with each other.
For the extracted iso-distances from the map, a test was performed using the following criteria, where value dataset correspond to the exact version using Saitho's algorithm, and prediction dataset correspond to the approximate Danielsson's algorithm:
If value{i, j, k} = 1 and prediction{i, j, k} = 1: T P = value is true positive.
if value{i, j, k} = 1 and prediction{i, j, k} = 0: FP = value is false positive.
if value{i, j, k} = 0 and prediction{i, j, k} = 0: T N = value is true negative.
if value{i, j, k} = 0 and prediction{i, j, k} = 1: FN = value is false negative.
In this context, accuracy is calculated from derived quantitative measurements of classified voxels as being true positives, false negatives, true negatives or false positives. With these measurements, specificity and sensitivity were also derived.
III. RESULTS
A. Comparison of Saitho and Danielsson (4SED) algorithms
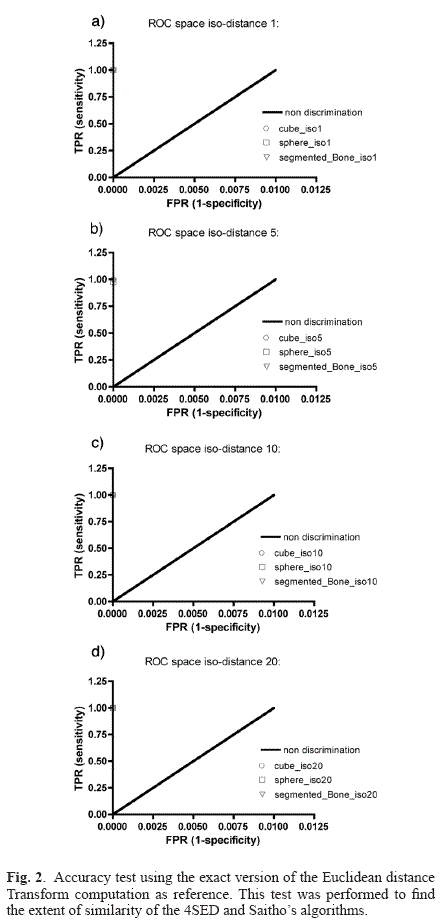
An accuracy test was computed on synthetic vffs volumes consisting of binary objects such as a cube and a sphere. Fig. 2 shows the graphs of the receiving operating characteristics (ROC) spaces derived from the test.
The results for each test are ploted to a ROC space as shown in Fig. 2. The results of the comparison of the equally extracted iso-distances 1, 5, 10, and 20 (in pixel units) from both implementations of the distance map calculation are summarized on Table 1, where it is clear that the average difference between both versions is 0.1%.
B. Computational time test
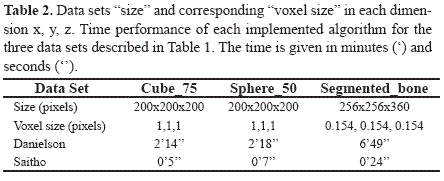
The volume data sets specifications are summarized in Table 2, and the respective time for the computation of the Euclidean distance transform is presented. The computational time, which was acquired using a timer, is the period of time that takes for each computation to be performed and obtained using the developed application.
C. Segmentation:
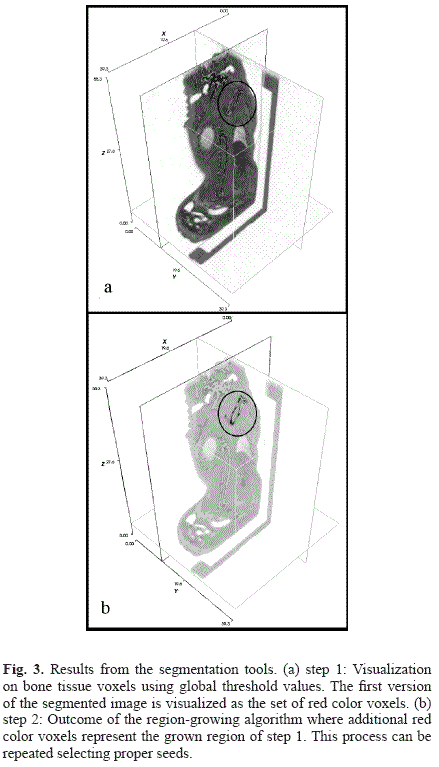
The results of the segmentation of a micro-CT dataset of a mouse are shown in Fig. 3. Fig. 3 a) shows the visualization of initially segmented bone using a global threshold value. This initial segmentation is a parcial version of the complete bone structure. This is due to the fact that only high intensity values are selected on a global thresholding operation, which will probably select the interior of the bones. This is the main reason why segmenting bone structures on micro-CT images datasets requires additional methods besides global thresholding. Region growing algorithms with local statistics computations as described on the methods section allows those other pixels on the boundary of bones to be segmented, because with the proposed method voxels are not only being segmented using intensity value criteria of each voxel separately, but considering the intensity of its neigborgs. As a result, the segmentation process only takes place if the information extracted from the neighbor voxels are within a range of statistical confidency. In Fig. 3 b) the outcome of the region-growing algorithm is visualized using the voxel V(88, 86, 261) as a seed.
D. GUI tool:
A view of the main GUI interface can be appreciated in Fig. 4. The software operates by modules, so that the user can concentrate in specific tasks without losing the overall computation of the distance transform.
A tool for the computation of the binary image is available and allows the preprocessing of the dataset to the desired binary representation. Fig. 5 shows the results for the preprocessing step to the distance transform calculation. The flow of information between modules or stages in the computation of the transformation is shown in Fig. 6.
IV. DISCUSSION
The results of the comparison of Saitho's and Danielsson 4SED algorithms have shown that there is no considerable difference between the extracted iso-distances that were computed using the exact version (Saitho's algorithm) and the ones extracted from the approximate version (Danielsson's 4SED algorithm), though variations are observed between datasets that have different geometry configuration. The highest accuracy in the whole range of evaluated iso-distances was for the cube dataset object (100% in 4 cases), for the sphere dataset object and the segmented-bone dataset. The average accuracy in the four cases was lower than 100% by only 0.1% and 0.125%, for the sphere and the segmented-bone datasets, respectively.
The computational time results from the performance test or what is called the computational cost of each version shows that for all datasets that were analyzed, the Saitho algorithm allows the fastest computation, as stated in the reviewed literature. This computational time test, revealed that in fact, the time required for the computation of the Euclidean distance transform in all datasets is image- size dependent, which also agrees with previous work in this field [9].
Other algorithms have been proposed to compute the signed Euclidean distance [8], or a faster version by propagation using multiple neighborhoods and bucket sorting [10]. These approaches could be evaluated in the future for cases where the signed map or a faster computation is needed.
Previous studies on the implementation of the Euclidean distance transforms suggest that an efficient computation can be reached just by modifying the approximate algorithms with the use of masks applied iteratively over the image (Yamada's EDT) or by morphological operations (Shih & Michel) [2]. The Saitho's algorithm was selected for implementation in this work based on a comparison of the Danielsson's four-point Sequential Euclidean distance mapping or 4SED algorithm and the Saitho exact algorithm implementations that was carried-out by means of an accuracy test and computing time test. This consideration did not take into account the possibility of using a modified version of Danielsson aproximate algorithm as proposed by other authors, because the performance of the exact version on Saitho's algorithm overheaded the performance of Danielsson's both in time and accuracy.
Regarding to the segmentation tasks, there are several methods used by others authors. The simple region-growing algorithms as described by Kang, Engelke et al. 2003 [9, 10], use global criteria to label voxels, but this usually leads to inexact results when complex structures are to be segmented. An improvement of this method is the use of neighborhood statistical computations as criteria of voxel inclusion in the segmented set of voxels as validated by Wang, Greenspan et al. 2006 [11, 12].
V. CONCLUSION
The computation of the Euclidean distance map transformation was showed to be feasible using the python programming language in conjunction with the vtk and itk toolkits. Both algorithms compute a scalar distance map from a 3D data set or volume, which can be used to extract specific distance values. The performance time for the Saitho computation was better than for the Danielsson's 4SED, allowing a faster calculation of the Euclidean distance map. There are two major components in the image analysis software program developed: the underlying segmentation method and the computation of the Euclidean distance map transformation, so that this application could be extended in the future to be used in conjunction with other image processing software applications.
VI. ACKNOWLEDGEMENT
The author would like to thank her supervisors, Dr. David Holdsworth and Dr. Maria Drangova and their collaborators at the imaging laboratories of the Robarts Research Institute, London, Ontario, Canada. Also would like to thank Steven Pollman for providing the synthetic images datasets used in this study and for his technical support and valuable discussions during the development of this project.
REFERENCES
[1] Cuisenaire O. Distance Transformations: Fast Algorithms and applications to Medical Image Processing, Laboratoire de Telocommunications et Teledetection, Docteur en Sciences Appliquees. Belgique: Universite catholique de Louvain, 1999. [ Links ]
[2] Marai G.E.; Laidlaw D.H.; Demiralp C.; Andrews S.; Grimm C.M.; Crisco J.J. Estimating joint contact areas and ligament lengths from bone kinematics and surfaces, Biomedical Engineering, IEEE Transactions, 51, 790-9, 2004. [ Links ]
[3] Marai G.E.; Laidlaw D.H.; Crisco J.J. Super-resolution registration using tissue-classified distance fields, Medical Imaging, IEEE Transactions, 25, 177-87, 2006. [ Links ]
[4] Ma B., Ellis R.E. Robust registration for computer-integrated orthopedic surgery: laboratory validation and clinical experience, Medical Image Analysis, 7(3) 237-250, September 2003. [ Links ]
[5] Frimmel H., Näppi J., Yoshida H. Fast and robust computation of colon centerline in CT colonography, Medical Physics, 31, 3046-56, 2004. [ Links ]
[6] Van Tonder G.J., Ejima Y. The patchwork engine: image segmentation from shape symmetries, Neural Networks, 13(3) 291-303, 2000. [ Links ]
[7] Van Biesen W., Sieben G., Lameire N., Vanholder R. Application of Kohonen neural networks for the non-morphological distinction between glomerular and tubular renal disease. Nephrology Dialysis Transplantation, 13(1) 59-66, 1998. [ Links ]
[8] Cuisenaire, OB. Fast Euclidean Distance Transformation by Propagation Using Multiple Neighborhoods, Computer Vision and Image Understanding, 76, 163-172, 1999. [ Links ]
[9] Kang Y., Engelke K., Kalender W.A. A new accurate and precise 3-D segmentation method for skeletal structures in volumetric CT data, Medical Imaging IEEE Transactions, 22, 586-98, 2003. [ Links ]
[10] Kang Y., Engelke K., Fuchs C., Kalender W.A. An anatomic coordinate system of the femoral neck for highly reproducible BMD measurements using 3D QCT. Computerized Medical Imaging and Graphics, 29(7) 533-541, 2005. [ Links ]
[11] Wang L.I., Greenspan M., Ellis R. Validation of bone segmentation and improved 3-D registration using contour coherency in CT data, Medical Imaging IEEE Transactions, 25, 324-34, 2006. [ Links ]
[12] Brennan D.D., Whelan P.F., Robinson K., Ghita O., O'Brien J.M., Sadleir R., Eustace S.J. Rapid Automated Measurement of Body Fat Distribution from Whole-Body MRI. American Journal of Roentgenology, 185, 418-423, August 2005. [ Links ]