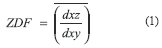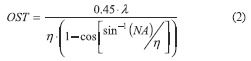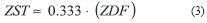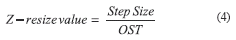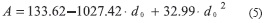Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares en
SciELO
Similares en
SciELO -
 Similares en Google
Similares en Google
Compartir
Revista Ingeniería Biomédica
versión impresa ISSN 1909-9762
Rev. ing. biomed. vol.3 no.6 Medellín jul./dic. 2009
MODELING DENDRITIC ARBORIZATION BASED ON 3D-RECONSTRUCTIONS OF ADULT RAT PHRENIC MOTONEURONS
MODELO DE ARBORIZACIÓN DENDRÍTICA BASADO EN RECONSTRUCCIONES DE MOTONEURONAS FRÉNICAS EN RATAS ADULTAS
Gabriel Obregón1,3, Leonid G. Ermilov1, Wen-Zhi Zhan1, Gary C. Sieck1,2, Carlos B. Mantilla1,2
1 Department of Physiology and Biomedical Engineering, Mayo Clinic, Rochester, United States.
2 Department of Anesthesiology, Mayo Clinic, Rochester, United States.
3 Programa de Ingeniería Biomédica. Escuela de Ingeniería de Antioquia-Universidad CES, Colombia. Contact e-mail: bmgaboh@eia.edu.co.
Received July 10, 2009. Accepted December 16, 2009
ABSTRACT
Stereological techniques that rely on morphological assumptions and direct three-dimensional (3D) confocal measurements have been previously used to estimate the dendritic surface areas of phrenic motoneurons (PhrMNs). Given that 97% of a motoneuron's receptive area is provided by dendrites, dendritic branching and overall extension are physiologically important in determining the output of their synaptic receptive fields. However, limitations intrinsic to shape-based estimations and incomplete labeling of dendritic trees by retrograde techniques have hindered systematic approaches to examine dendritic morphology of PhrMNs. In this study, a novel method that improves dendritic filling of PhrMNs in lightly-fixed samples was used. Confocal microscopy allowed accurate 3D reconstruction of dendritic arbors from adult rat PhrMNs. Following pre-processing, segmentation was semi-automatically performed in 3D, and direct measurements of dendritic surface area were obtained. A quadratic model for estimating dendritic tree surface area based on measurements of primary dendrite diameter was derived (r2 = 0.932; p<0.0001). This method may enhance interpretation of motoneuron plasticity in response to injury or disease by permitting estimations of dendritic arborization of PhrMNs since measurements of primary dendrite diameter can be reliably obtained from a number of retrograde labeling techniques.
KEY WORDS: 3D Reconstruction, Intracellular injection, Phrenic motoneuron, Volume segmentation.
RESUMEN
El área superficial de las dendritas en motoneuronas frénicas (PhrMNs) ha sido estimada anteriormente mediante técnicas estereológicas basadas en suposiciones geométricas, y medida en tres dimensiones (3D) utilizando microscopía confocal. Dado que el 97% del área receptora de una motoneurona corresponde a sus dendritas, la ramificación y extensión dendrítica son fisiológicamente importantes para determinar la salida de sus campos receptivos. Sin embargo, limitaciones inherentes a las estimaciones basadas en morfología neuronal y la tinción incompleta de los árboles dendríticos mediante técnicas retrógradas han dificultado los estudios sistemáticos de la morfología dendrítica en PhrMNs. En este estudio, se utilizó una nueva técnica que mejora la tinción dendrítica de las PhrMNs en preparaciones fijadas ligeramente. La reconstrucción dendrítica en 3D se logró con gran precisión utilizando microscopía confocal en PhrMNs de ratas adultas. Luego de una etapa de pre-procesamiento, la segmentación de los árboles dendríticos se realizó semi-automáticamente en 3D y usando mediciones directas del área superficial, se derivó un modelo cuadrático para estimar dicha área partiendo del diámetro de la dendrita primaria (r2 = 0.932; p<0.0001). Este método podría mejorar la evaluación de la plasticidad neuronal en respuesta a trauma u otras enfermedades permitiendo la estimación de la arborización dendrítica en PhrMNs, ya que el diámetro de la dendrita primaria puede obtenerse confiablemente de numerosas técnicas de tinción retrógrada.
PALABRAS CLAVE: Inyección intracelular, Motoneurona frénica, Reconstrucción en 3D, Segmentación volumétrica.
I. INTRODUCTION
Motoneurons innervate skeletal muscles and together are the final element of motor control. Respiratory motoneurons, including those innervating the diaphragm muscle-phrenic motoneurons (PhrMNs), are highly active throughout the lifespan [1]. Like most mammalian neurons in the central nervous system, PhrMNs receive synaptic contacts at the soma and dendrites, with more than 97% of their receptive area being supplied by dendrites [2]. Dendritic arbors serve to integrate multiple synaptic inputs along their length, in accordance with the timing and amplitude of individual inputs [3] and are highly plastic both in the extent and nature of synaptic connections [4]. For example, altered dendritic arbors are present in several neuropathological conditions including mental retardation syndromes such as Down, Rett's and Fragile X syndromes, schizophrenia and Alzheimer's disease [5]. Clearly, the branching and overall extension of motoneuron dendrites is physiologically important in determining the output of their synaptic receptive fields.
Previous studies on motoneuron morphometry have used stereological techniques that rely on geometrical assumptions about object size, shape, and orientation to estimate cell body and dendritic volumes and surface areas from two dimensional (2D) images [6]. Burke et al. [7] devised a simple stochastic model (Monte Carlo) to simulate or mimic the variability of fully formed, adult motoneuron branching dendritic trees. In their analysis, the surface areas of 64 reconstructed gastrocnemius α-motoneuron dendrites (from cat spinal cords) were correlated to the dendritic stem diameter (measured 15 µm from the soma) through a least-square power function. Hypothesizing that the primary dendrite diameter could be sufficient to describe the quantitative features of other types of motoneurons, we decided to evaluate this parameter in our study. Moschovakis et al.[8] proposed that the surface area distal to a given dendritic branch relates to the square of the parent end diameter.
A three dimensional (3D) morphological method based on stacks of confocal images of retrogradely labeled PhrMNs has been described previously [6,9-11]. However, retrograde labeling methods commonly result in incomplete filling of the dendritic trees. Recently, a novel method to improve dendritic filling of PhrMNs in lightly-fixed samples was developed. Using completely filled PhrMN dendrites from the adult rat, we derived a model for estimating dendritic tree surface area based on measurements of primary dendrite diameter obtained from 3D reconstructions, without morphological assumptions.
II. MATERIALS AND METHODS
General remarks:
The study consisted of 6 adult (280-300 g initial body wt) male Sprague-Dawley rats (Harlan Sprague-Dawley, Indianapolis, IN). All procedures involving animals were in strict accordance with the guidelines established by the American Physiological Society and were approved by the Institutional Animal Care and Use Committee of the Mayo Clinic.
2.1 Tissue preparation:
Methods and preliminary results for intracellular injection of retrogradely-labeled PhrMNs in lightly-fixed sections of the rat adult spinal cord were presented in abstract form [12].
- Retrograde-labeling of PhrMN
Briefly, adult rats were anesthetized using a mixture of ketamine (60 mg/kg body wt) and xylazine (2.5 mg/ kg body wt). PhrMNs were specifically labeled by intrapleural injection of Alexa Fluor 488-conjugated cholera toxin fragment B (CTB, Invitrogen Corp. Carlsbad, CA) [13].
After a 72-h survival period and using a modification of the method described by Pace et al.[13], animals were re-anesthetized as above, transcardially injected with heparinized saline and fixed with 4% paraformaldehyde and 4% sucrose in 0.1M phosphate buffer.
Cervical spinal cords (C3-C6) were excised, postfixed and embedded in agarose. Longitudinal sections were cut at 150 µm using a VT1000S Vibroslicer (Leica, Bannockburn, Ill). Sections containing the ventral horns were placed at the bottom of a sylgard-lined dish.
- PhrMN visualization and lucifer yellow (LY) injection
Retrogradely-labeled PhrMNs were visualized using a Photometrics Cascade CCD camera mounted on an Olympus upright microscope. Appropriate excitation and emission filters were used for Alexa 488 fluorescence. Labeled motoneurons were injected using customfabricated micropipettes filled with a 2% aqueous solution of LY (Sigma-Aldrich Corp., excitation/emission maxima: 425/528 nm) and 0.5 M lithium chloride. Negative current pulses (100 ms; 3-4 Hz; 1-1.5 nA) were generated through the microelectrode with a Grass S88 stimulator (Grass Medical Instruments, Quincy, Mass.) [15-16].
Spinal cord sections were then mounted on gelatin-subbed slides, processed in graded alcohols, and coverslipped with DPX mounting media (Gallard- Schlesinger Ind.).
2.2 Confocal imaging:
- System setup
An Olympus FluoView 200 laser-scanning confocal system mounted on an upright Olympus BX50WI microscope was used. The step size for each optical section was controlled via a Z-axis stepper motor attached to the focusing knob of the microscope.
A 488 nm Argon laser was used to excite the LY-injected PhrMNs, and for imaging FITC-labeled microspheres used for empirical validation (described below). An Olympus 60x oil-immersion objective lens (N.A. = 1.4; working distance = 210 µm), and low-fluorescence immersion oil were used throughout the study. Optical sections were made parallel to the microscope stage (XY plane).
- Image acquisition
Images were digitized at 12-bit resolution (0 - 4095 gray levels; GL) into arrays of 800x600 pixels using Fluoview software version 5 (Olympus). XY pixel dimensions were 0.333x0.333 µm; thus, each image spanned 267x200 µm. Optical sectioning was conducted by moving the stage in a single direction (0.8 µm Z-steps) to eliminate backlash error in the stepper motor [6,11].
Initially, fluorescently injected PhrMNs were located using a 10x objective under an epifluorescence lamp and appropriate emission filters. In order to reconstruct dendritic trees that extended beyond the plane of view, a sequence of adjacent image stacks were captured for each PhrMN making sure that images on all sides of visible neuronal structures were included [15].
2.3 Three dimensional reconstruction
- Z - Distortion
Several factors such as stepper motor inaccuracy, tissue compression, and a mismatch amongst the refractive indexes of the tissue, mounting medium, and objective lens immersion oil, may affect the measurements of confocal optical sections [11]. Additionally, optical systems introduce diffraction-based distortion that is manifest by the spreading of an ideal point object (subresolution) into circumferential "Airy" discs of progressively lower intensity. These factors, in general, introduce worse distortion along the Z- axis [10]. Thus, overall correction factors for taking morphological measurements had to be empirically determined.
- Z - distortion factor
Fluorescently labeled microspheres (10-µm in diameter) were imaged at 0.325 µm steps; the step size was chosen to approximate the XY pixel dimensions. Images of microspheres were loaded and 3D-rendered as isotropic volumes (0.333x0.333 x0.333 µm) using ANALYZE (a comprehensive image display and manipulation package [18]; Biomedical Imaging Resource, Mayo Foundation), and the out-of-focus flare and background noise were thresholded using one of the software's tools. The diameters were measured on both the XZ and XY planes and the Z-distortion factor (ZDF) was calculated (1) as the mean ratio between these values.
- Slice thickness
The optical slice thickness (OST) or Z-axis resolution at the optimal confocal aperture is given by (2), and depends on the numerical aperture of the objective lens (NA), the excitation wavelength (λ) and the refractive index (η) of the surrounding medium and tissue [10].
Even though the techniques for estimating the OST have been described in detail elsewhere [6], for the purpose of this study (Section 4.3), overall Z-distortion was evenly accounted for throughout every optical section, and the resulting Z-slice thickness (ZST) was empirically calculated (3) as the product between ZDF and voxel dimension:
- Z - resize value
Matching the OST and the step size, as defined by the stepper motor, determines the optimal sampling conditions in the Z-axis and ultimately, the accuracy of the volume measurements. The use of a step size smaller than the OST results in oversampling: repeated sampling of similar planes. In contrast, larger step sizes than the OST result in undersampling of the specimen and consequently, in a loss of information [10].
PhrMNs were imaged with a larger step size to minimize photobleaching. Thus, the quotient between the step size used for imaging PhrMNs (0.8 µm) and the ZST was defined as the Z-resize value (4), i.e., the depth assigned to every pixel on the stack of digitized images prior to 3D-rendering. By doing so, the impact of sampling conditions and Z-distortion were considered in creating 3D-rendered images.
- Image resizing and volume rendering
A linear interpolation method (custom-designed in ANALYZE) was used to resize confocal image stacks in order to view anisotropic volumes as isotropic with proper aspect ratios (using the highest spatial resolution per voxel). After interpolation, image stacks were cut down by manually removing planes without neuronal content in order to expedite processing.
Finally, using a fuzzy-gradient-shading algorithm in ANALYZE [6,11], each set of optical sections was 3D-rendered (minimum threshold = 80 GL, maximum threshold = 4,095 GL).
2.4 3D Dendritic segmentation and morphometry
Only dendritic trees with minor mechanical damage caused by spinal cord sectioning, within the working distance of the objective lens and showing branching greater than secondary order were used for morphological analyses. Volume rendering tools available in ANALYZE were used for all aspects of image segmentation and analysis.
- Image denoising
A 3D median filter transformation (kernel size = 3x3x3) was performed on the input volumes to enhance the signalto- noise ratio. The remaining background noise (inherent to the optical system and corresponding to the tissue's natural autofluorescence) was manually traced and deleted from areas surrounding PhrMNs by using different threshold levels and spatial orientations with volume editing and rotation tools. A Seeded Region Growing Method, with one or more seeds, was used to define and keep 3D regions based on connectivity (6-connected, i.e., 3D neighbors).
- Object maps
Based on fluorescence intensity, voxels comprising the dendritic trees of interest were assigned to specific object maps, i.e., one-to-one copies of a volume in which the voxel intensities dictate object membership. Object creation started at the end of the primary dendritic hillock, after which dendritic diameter was fairly uniform. Given differences in fluorescence intensity along the length of individual dendritic trees, more than one object was created and sequential objects were later re-assigned into a single object per primary dendrite.
- Surface area measurements
The newly created dendritic tree objects were displayed separately and surface area measurements were taken from the 3D reconstructions using a surface-tracking algorithm [11]. Sequential image stacks containing redundant information (imaged this way to minimize loss of neuronal content) were registered manually in 3D using object masks, which were then subtracted from one of the stacks to avoid duplication. Outer-most voxel counts were multiplied by the square of the XY resolution to provide surface area in microns.
- Primary dendrite diameter measurements
For each primary dendrite, diameter was measured using a line measuring tool at ~15 µm from the soma (curved distance from the end of the primary dendritic hillock) [11] by interactively rotating the objects to the major-axis diameter view.
2.5 Dendritic arborization models
Dendritic tree surface area measurements were compared to primary dendritic diameters and linear, power, and quadratic curves were plotted to fit the data. Pearson correlation was performed for each model fit using Sigma Plot 11.0 (SAS Inc.).
III. RESULTS
3.1. PhrMN Visualization and LY Injection
Numerous PhrMNs were visible within the ventral horns of C3-C6 spinal cord segments following intrapleural injection with Alexa 488-CTB, consistent with previous reports [11,18-19]. PhrMN somata were distributed across three to four tissue sections spanning 450-600 µm in the axial plane. However, labeling of individual PhrMNs was incomplete, with poor delineation of neuronal features and dendrites. Alexa 488-labeling was useful for guiding the LY-microelectrode through the membrane of superficiallylocated PhrMNs within the lightly-fixed tissue. Complete filling of multipolar PhrMNs, including dendritic trees, was possible after a 10-20 min injection of LY.
3.2 Confocal imaging and 3D reconstruction
In the XY plane, the measured diameter of the microspheres closely matched the specifications of the manufacturer. Table 1 summarizes the parameters that were empirically calculated to correct for overall distortion in the Z-axis, when using a step size of 0.8 µm.
Depending on the location of PhrMNs within a tissue slice, image sets ranged from 76 to 158 optical sections starting from the top surface. Maximum intensity projections were used to evaluate structural details including dendritic branching prior to 3D reconstruction, segmentation and morphometry. A total of 7 PhrMNs from 4 animals were selected based on the branching (> 2nd order) of at least one primary dendritic tree.
3.3 3D Dendritic tree segmentation
Eleven full dentritic arbors showing minor mechanical damage were semi-automatically segmented and assigned to objects based on voxel intensities. Fig. 1 shows fuzzygradient volume renderings of dendritic tree objects created from optical sections of adult rat PhrMNs.
3.4 3D Dentritic tree morphometry
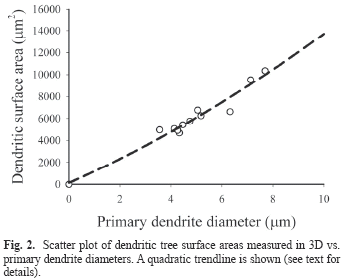
Dendritic branching ranged from 3rd to 7th order. Mean primary dendrite diameters and dendritic arbor surface area were 5.2 ± 1.3 µm and 6,391 ± 1,895 µm2, respectively.
All three fitting models (linear, quadratic and power) demonstrated significant correlation between dendritic tree surface area (A) and primary dendrite diameter (d0). Pearson values for the linear, power and quadratic models were (r2 = 0.949; p<0.001), (r2 = 0.953; p<0.0001) and (r2 = 0.955; p<0.0001) respectively. A fitted quadratic curve (5) is shown in Fig. 2.
IV. DISCUSION
4.1 Dendritic tree morphometry
In the surface area estimation model introduced by Burke et al. [7], dendrites were measured as successions of cylindrical segments, each having a constant diameter and a measured length [20], and branching points (regions where individual branches are linked to a stem branch) were assumed as being dichotomous. However, shape-based assumptions may yield inaccurate results. For example, Prakash et al. [6] showed that stereological methods can overestimate PhrMN soma volumes by up to 300% in cases where the relationship between axial and lateral dimensions deviate from shape assumptions (prolate spheroid). In our study, confocal microscopy allowed for accurate reconstruction of dendritic trees along all axes, and therefore direct measurements of PhrMN surface areas were possible without assumptions of dendrite shape (i.e., cylindrical) or taper rate.
In the present study, dendrites were sampled based on their branching into at least tertiary order. Thus, only dendritic arbors known to be fully reconstructed were used in the model. However, some dendrites showed minimal branching despite considerable length. It is possible that our criteria for inclusion will overestimate branching and thus dendritic surface area. Including dendrites with minimal branching did not change the relationship between primary dendrite diameter and overall dendritic surface area (r2 = 0.545 for a quadratic model; p=0.0002), with a narrow 95% confidence interval for primary dendrite diameters between 2 and 8 µm. In order to empirically validate the model, however, a greater sample of PhrMNs should be analyzed across different developmental time points. Our average primary dendrite diameter was 5.2 µm, which is larger than that previously reported with CTB-based retrograde labeling techniques (e.g., 2.7 µm) [11]. It is likely that these differences reflect the better dendritic filling with LY and incomplete filling (mainly via intracellular organelles) with CTB.
4.2 PhrMN visualization and LY injection
Intrapleural injection with Alexa 488-CTB provides highly specific labeling of PhrMNs [12] and allows the focused impalement of numerous cell bodies with a fluorescent-dye containing microelectrode. However, on multiple opportunities, leakage of LY into the surrounding medium prevented imaging of adult PhrMNs. This could be a consequence of using a dye with a small molecular weight (457 Da) or could be related to the method of tissue-fixation being employed although similar experiments in younger rats (P21 or P28; data not shown) do not seem to be associated with such rate of dye loss. Even though the dendritic fields are primarily oriented in the horizontal plane, parallel to the plane of tissue sectioning [11], sometimes major mechanical damage of superficially located dendritic trees with a ventrodorsal orientation can happen. In turn, this could result in dye leakage. Regardless, detailed morphometric analyses of the dendritic trees of adult motoneurons were possible with highly reliable and accurate 3D representations of dendritic branching.
4.3 Confocal imaging, image resizing and volume rendering
Confocal microscopes are very powerful tools for direct 3D-structural analysis based on their ability to suppress out-of-focus information and to spatially-register sequential optical sections [6,10]. Optimal sampling through optical sectioning and faithful reproduction of shape and size along the Z-axis are therefore notable strengths of these systems. However, empirical calibration and validation of the specific confocal set-up must be conducted for each imaging application when accurate 3D reconstructions are paramount. For example, direct volume measurements of microscopic fluorescentlylabeled beads may show up to 17% overestimation of bead volume (compared to manufacturer's specification) without empirical calibration procedures [6,10]. In the present study, we found that the distortion introduced along the Z-axis would result in a ~24% overestimation of an object's volume.
The mismatch between OST and step size introduces the greatest error when measuring volumes using confocal microscopy [10]. However, various factors including lens properties decrease the actual Z-axis resolution. Z-distortion increases when imaging close to the limits of the lens' working distance. Therefore, instead of trying to achieve the best possible Z-axis resolution (usually twice the XY resolution), the main goal in several practical applications involving volume measurements is to account for Z-distortion by empirically determining it in each application. Furthermore, sampling at an optimal step size usually produces large sets of data with high computational demands, and may lead to photobleaching and tissue damage. Hence, an unbiased interpolation technique that allows undersampling with minimal loss of information was used. Similar techniques such as the Cavalieri principle have been verified extensively [9-10].
4.4 3D Dendritic tree segmentation
Due to the fact that LY and Alexa 488 have close excitation/emission wavelengths, retrogradely-labeled PhrMNs surrounding the injected cells, introduce large amounts of low-contrast background noise. Natural tissue autofluorescence, at the given excitation wavelength (488 nm), is also a major source of noise. Additionally, the fluorescence signal is not uniform throughout the whole extension of the dendrites, and tends to progressively fade away. Thus, object extraction can prove challenging despite optimal imaging conditions. It is possible that injection of a far red-dye could improve signal to noise ratio and ease the segmentation process.
Automated object extraction of neuronal processes from large stacks of 3D confocal images is essential for quantitative neuroanatomy and neuronal assays. Basically, two major approaches are described in the literature [20] -one based on 2D/3D skeletonization algorithms [22-24] and another based on sequential tracing (vectorization) along neuronal processes [25-27]. Simply put, in skeletonization, an image volume is segmented and/or binarized in order to automatically extract the foreground, and the resulting binary image is systematically thinned up to the skeleton of the neurite, which is further processed. In vectorization, the tube-like structure of neurites is used to trace them sequentially from seed points that can be specified manually or extracted automatically. Importantly, some of these methods rely on pre-processing that optimally results in background removal and denoising [27], and are still based on simple assumptions regarding neurite morphology [26]. In the present work, we used semi-automated segmentation algorithms in order to avoid needing morphological assumptions. Clearly, these novel automated dendritic extraction methods may be implemented in our 3D stacks of PhrMN images, but comparison across these methods is outside of the scope of this report.
Median spatial filtering proved to be a highly effective method for enhancing the signal-to-noise ratio, consequentially improving signal contrast. In addition, filtering aided in distinguishing dendrites from different motoneurons traversing in close proximity. However, filtering adds surface features on medium-intensity objects and enhances high-intensity regions (e.g., surrounding PhrMN cell bodies not intracellularly injected). To account for the effects of filtering on morphometric analyses, kernel size was empirically established through trial and error in this application. Additional removal on surrounding "noise" was conducted manually, although seed-based object-growing algorithms may prove useful for this purpose. Variations in thresholding can considerably affect surface area measurements, and thus a set of criteria have to be defined and applied consistently both in semiautomated and automated extraction algorithms.
V. CONCLUSION
A novel model for estimating dendritic surface area based on measurements of primary dendrite diameter was derived using 3D reconstructions of intracellularly-filled adult rat PhrMNs, without morphological assumptions. The dendritic surface area of all branches of a primary dendrite shows a highly significant correlation with dendrite diameter at 15 µm from the soma. However, further analyses, in which completely automated neurite-tracing algorithms could be incorporated, will be needed to validate the dendritic model proposed in this report for PhrMNs across developmental time points. A simple model of dendritic structure based on a minimal number of morphological parameters of the primary dendrites may be useful in studies of motoneuron plasticity following injury or disease, since measurements of primary dendrite diameter can be readily and reliably obtained using optical microscopy methods. In this method, intracellular fills of multiple motoneurons are possible, overcoming existing sampling limitations with in vivo or slice preparations where only few motoneurons per animal can usually be injected. By retrogradely-labeling PhrMNs prior to tissue sectioning, these become visible and thus it is possible to specifically fill only motoneurons of interest.
ACKNOWLEDGEMENT
This research was supported by NIH grants AR055173 and HL037680 and the Mayo Foundation. The authors wish to thank Mr. Paul T. Weavers for technical assistance.
REFERENCES
[1] Mantilla C.B., Sieck G.C. Trophic factor expression in phrenic motor neurons. Respiratory Physiology and Neurobiology, 164, 252-262, 2008. [ Links ]
[2] Kernell D., Zwaagstra B. Size and remoteness: two relatively independent parameters of dendrites, as studied for spinal motoneurones of the cat. The journal of physiology, 413, 233-54, 1989. [ Links ]
[3] Mel B.W. Synaptic integration in an excitable dendritic tree. Journal of Neurophysiology, 70, 1086-101, 1993. [ Links ]
[4] Wong R.O., Ghosh A. Activity-dependent regulation of dendritic growth and patterning. Nature reviews neuroscience, 3, 803-812, 2003. [ Links ]
[5] Vallotton P., Lagerstrom R., Sun C., Buckley M., Wang D., De Silva M., Tan S., Gunnersen J.M. Automated analysis of neurite branching in cultured cortical neurons using HCAVision. Cytometry A, 71A, 10, 889-895, 2007. [ Links ]
[6] Prakash Y.S., Smithson K.G., Sieck G.C. Measurements of motoneuron somal volumes using laser confocal microscopy: comparisons with shape-based stereological estimations. Neuroimage, 1, 95-107, 1993. [ Links ]
[7] Burke R.E., Marks W.B., Ulfhake B. A parsimonious description of motoneuron dendritic morphology using computer simulation. The journal of neuroscience, 12, 2403-2416, 1992. [ Links ]
[8] Moschovakis A.K., Burke R.E., Fyffe R.E. The size and dendritic structure of HRP-labeled gamma motoneurons in the cat spinal cord. The journal of comparative neurology, 311, 531-545, 1991. [ Links ]
[9] Prakash Y.S., Smithson K.G., Sieck G.C. Application of the Cavalieri principle in volume estimation using laser confocal microscopy. Neuroimage, 1, 325-333, 1994. [ Links ]
[10] Sieck G.C., Mantilla C.B., Prakash Y.S. Volume measurements in confocal microscopy. Methods enzymology, 307, 296-315, 1999. [ Links ]
[11] Prakash Y.S., Mantilla C.B., Zhan W.Z., Smithson K.G., Sieck G.C. Phrenic motoneuron morphology during rapid diaphragm muscle growth. Journal of applied physiology, 89, 563-72, 2000. [ Links ]
[12] Ermilov L.G., Zhan W., Issa A.N., Sieck G.C., Mantilla C.B. Enhanced three-dimensional visualization of phrenic motoneurons. Experimental Biology 2009. [ Links ]
[13] Mantilla C.B., Zhan W.Z., Sieck G.C. Retrograde labeling of phrenic motoneurons by intrapleural injection. Journal of neuroscience methods, 182, 244-249, 2009. [ Links ]
[14] Pace C.J., Tieman D.G., Tieman S.B. Intracellular injection in fixed slices: obtaining complete dendritic arbors of large cells. Journal of neuroscience methods, 119, 23-30, 2002. [ Links ]
[15] Ermilov L.G., Miller S.M., Schmalz P.F., Hanani M., Szurszewski J.H. The three-dimensional structure of neurons in the guinea pig inferior mesenteric and pelvic hypogastric ganglia. Autonomic Neuroscience, 83, 116-26, 2000. [ Links ]
[16] Ermilov L.G., Miller S.M., Schmalz P.F., Hanani M., Lennon V.A., Szurszewski J.H. Morphological characteristics and immunohistochemical detection of nicotinic acetylcholine receptors on intestinofugal afferent neurones in guinea-pig colon. Journal of the European Society of neurogastroenterology and motility, 15, 289-98, 2003. [ Links ]
[17] Robb R.A., Hanson D.P., Karwoski R.A., Larson A.G., Workman E.L., Stacy M.C. ANALYZE: A comprehensive, operator-interactive software package for multidimensional medical image display and analysis. Comput med imaging graph, 13, 433-454, 1989. [ Links ]
[18] Goshgarian H.G., Rafols J.A. The phrenic nucleus of the albino rat: a correlative HRP and Golgi study. The journal of comparative neurology, 201, 441-456, 1981. [ Links ]
[19] Lindsay A.D., Greer J.J., Feldman J.L. Phrenic motoneuron morphology in the neonatal rat. The journal of comparative neurology, 308, 169-179, 1991. [ Links ]
[20] Cullheim S., Fleshman J.W., Glenn L.L., Burke R.E. Membrane area and dendritic structure in type-identified triceps surae alpha motoneurons. The journal of comparative neurology, 255, 68-81, 1987. [ Links ]
[21] Al-Kofahi Y., Dowell-Mesfin N., Pace C., Shain W., Turner J.N., Roysam B. Improved detection of branching points in algorithms for automated neuron tracing from 3D confocal images. Cytometry A, 73A, 36-43, 2008. [ Links ]
[22] Al-Kofahi KA, Lasek S, Szarowski DH, Pace CJ, Nagy G, Turner JN, Roysam B. Rapid automated three-dimensional tracing of neurons from confocal image stacks. IEEE Transactions on information technology in biomedicine, 6, 171-187, 2002. [ Links ]
[23] Dima A., Scholz M., Obermayer K. Automatic segmentation and skeletonization of neurons from confocal microscopy images based on the 3-D wavelet transform. IEEE Transactions on image processing, 11, 790-801, 2002. [ Links ]
[24] Cohen A., Roysam B., Turner J. Automated tracing and volume measurements of neurons from 3-D confocal fluorescence microscopy data. Journal of microscopy, 173, 103-114, 1994. [ Links ]
[25] He W., Hamilton T.A., Cohen A.R., Holmes T.J., Pace C., Szarowski D.H., Turner J.N., Roysam B. Automated threedimensional tracing of neurons in confocal and brightfield images. Microscopy and microanalysis, 9, 296-310, 2003. [ Links ]
[26] Zhang Y., Zhou X., Lu J., Lichtman J., Adjeroh D., Wong S.T.C. 3-D axon structure extraction and analysis in confocal fluorescence microscopy images. Neural computation, 20, 8, 1899-1927, 2008. [ Links ]
[27] Yu W., Lee H.K., Hariharan S., Bu W., Ahmed S. Quantitative neurite outgrowth measurement based on image segmentation with topological dependence. Cytometry A, 75A, 289-297, 2009. [ Links ]