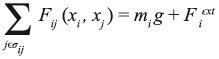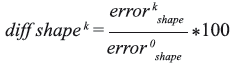Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares en
SciELO
Similares en
SciELO -
 Similares en Google
Similares en Google
Compartir
Revista Ingeniería Biomédica
versión impresa ISSN 1909-9762
Rev. ing. biomed. vol.4 no.8 Medellín jul./dic. 2010
GENERAL ALGORITHMS FOR LAPAROSCOPIC SURGICAL SIMULATORS
ALGORITMOS GENERALES PARA SIMULADORES DE CIRUGÍA LAPAROSCÓPICA
Christian Diaz1, Helmuth Trefftz2, Jorge Bernal3, Steven Eliuk4
1 PhD candidate, Virtual Reality Laboratory, EAFIT University, Medellin, Colombia. cdiazleo@eafit.edu.co.
2 Associated Professor, Virtual Reality Laboratory, EAFIT University, Medellin, Colombia.
3 Director, Laparoscopic Surgery Research Group, CES University, Medellin, Colombia.
4 PhD candidate, Advanced Man Machine Interface Laboratory (AMMi), University of Alberta, Edmonton, Canada.
Received November 25, 2010. Accepted December 29, 2010
ABSTRACT
Recent advances in fields such as modeling of deformable objects, haptic technologies, immersive technologies, computation capacity and virtual environments have created the conditions to offer novel and suitable training tools and learning methods in the medical area. One of these training tools is the virtual surgical simulator, which has no limitations of time or risk, unlike conventional methods of training. Moreover, these simulators allow for the quantitative evaluation of the surgeon performance, giving the possibility to create performance standards in order to define if the surgeon is well prepared to execute a determined surgical procedure on a real patient.
This paper describes the development of a virtual simulator for laparoscopic surgery. The simulator allows the multimodal interaction between the surgeon and the surgical virtual environment using visual and haptic feedback devices. To make the experience of the surgeon closer to the real surgical environment a specific user interface was developed. Additionally in this paper we describe some implementations carried out to face typical challenges presented in surgical simulators related to the tradeoff between real-time performance and high realism; for instance, the deformation of soft tissues are simulated using a GPU (Graphics Processor Unit) -based implementation of the mass-spring model. In this case, we explain the algorithms developed taking into account the particular case of a cholecystectomy procedure in laparoscopic surgery.
KEY WORDS: Medical training, Minimally invasive surgery, Surgical simulation, Virtual reality.
RESUMEN
Recientes avances en áreas tales como modelación computacional de objetos deformables, tecnologías hápticas, tecnologías inmersivas, capacidad de procesamiento y ambiente virtuales han proporcionado las bases para el desarrollo de herramientas y métodos de aprendizaje confiables en el entrenamiento médico. Una de estas herramientas de entrenamiento son los simuladores quirúrgicos virtuales, los cuales no tienen limitaciones de tiempo o riesgos a diferencia de los métodos convencionales de entrenamiento. Además, dichos simuladores permiten una evaluación cuantitativa del desempeño del cirujano, dando la posibilidad de crear estándares de desempeño con el fin de definir en qué momento un cirujano está preparado para realizar un determinado procedimiento quirúrgico sobre un paciente.
Este artículo describe el desarrollo de un simulador virtual para cirugía laparoscópica. Este simulador permite la interacción multimodal entre el cirujano y el ambiente virtual quirúrgico usando dispositivos de retroalimentación visual y háptica. Para hacer la experiencia del cirujano más cercana a la de una ambiente quirúrgico real se desarrolló una interfaz cirujano-simulador especial. Adicionalmente en este artículo se describen algunas implementaciones que solucionan los problemas típicos cuando se desarrolla un simulador quirúrgico, principalmente relacionados con lograr un desempeño en tiempo real mientras se sacrifica el nivel de realismo de la simulación: por ejemplo, la deformación de los tejidos blandos simulados usando una implementación del modelo masa-resorte en la unidad de procesamiento gráfico. En este caso se describen los algoritmos desarrollados tomando en cuenta la simulación de un procedimiento laparoscópico llamado colecistectomía.
PALABRAS CLAVE: Entrenamiento médico, cirugía mínimamente invasiva, simulación quirúrgica, realidad virtual.
I. INTRODUCTION
Since mid-1980, the introduction of the compact CCD (Charge Coupled Device) camera made the laparoscopic surgery feasible allowing its quick introduction in the everyday medical surgical procedures. Due to its promising results, such as shorter recovery time and less risk of infection, it was widely adopted.
Soon, the demand to execute these procedures in clinical practice increased and surgeons were expected to adopt these procedures. This adoption can be possible due to the simplicity of some pioneer procedures in this new surgical area. However, the creation of new procedures with greater complexity and the technical risks, present in these innovative surgical tasks, leads the surgeon to make the mistakes and cause injuries in the patient during execution of these surgical procedures. For example, in the extraction of the gallbladder, an incorrect interpretation of the anatomy can result in an injury of the bladder duct. The treatment of this injure is complicated and sometimes, it requires a second surgical intervention [1].
The training process for laparoscopic surgery is currently based on a combination of several techniques of training and education, for example, training manual skills in real surgeries supervised by an expert, using live animals or in-vitro models based on synthetic materials, and training cognitive skills using informative CD's, videos and books. These techniques have disadvantages such as expensive prices, the high risk for the patient, limited time to train, low realism of the simulation of the real human anatomy, amongst others. These disadvantages limit the efficacy of the training method, therefore increasing the surgeon's stress level and decreasing his creativity to innovate creating new procedures [2].
The advances of new technologies in fields such as physical simulation of deformable objects and virtual environments have created the conditions for virtual surgical training systems to meet all key elements required to obtain an efficient outcome. The virtual laparoscopic simulators have no limitations of time, or risk unlike conventional methods of training, which could further jeopardize the health and even the lives of patients. Moreover, these simulators can reproduce the real human anatomy with greater accuracy, including pathologies and anatomical variations, which the surgeon can face up in a real procedure, and that are difficult to simulate using other training techniques. For example, in the conventional training method the trainee must wait for one patient with the pathology in order to be able to train it.
This paper presents some of the algorithms required to develop a virtual simulator of laparoscopic surgery. The simulator allows the multimodal interaction between the surgeon and the surgical virtual environment using visual and haptic feedback devices. In order to make the experience of the surgeon closer to the real surgical environment, a specific user interface was developed. In this case, we explain the algorithms developed taking into account the particular case of a cholecystectomy procedure in laparoscopic surgery [3].
The rest of the paper is organized as follows: Section 2 describes similar projects. Section 3 describes each component developed in the surgical simulator. Section 4 and 5 describes the obtained results and the discussion. Finally, section 6 describes the conclusions reached so far and the future work.
II. RELATED WORK
Due to the limitations of the medical area to train surgical procedures of high complexity and the technological advances in the informatics technology, biomechanics modeling and virtual environments during the mid-90's, several research groups around the world pursued projects to develop virtual environments in order to train surgeons in minimally invasive surgery. In this way, several projects have been carried out in the surgery simulation area with a broad range of medical applications, such as: laparoscopic surgery [4,5], virtual endoscopy [6], arthroscopy [7], microsurgery [8], extraction of colon tumors [9], intraocular surgery [10], amongst others. These different simulators have demonstrated the utility of the virtual simulators in medical training.
The development of surgical simulators has demanded advances in different research topics, which have contributed to the development of surgical simulators with high realism and real-time performance. In particular, there are four research topics, each of which has reviews dedicated summarizing the research steps followed by the scientific community. These topics include: deformable objects simulation [11], collision detection [12], simulation of topological changes [13] and design and development of simulator-surgeon interfaces [14].
Specifically, in the development of simulators to train the cholecystectomy procedure several approaches have been taken [15], applying the algorithms and methods developed in the research topics mentioned before. Moreover corporations dedicated to develop and market surgical simulators have created training systems for these types of procedures [16]. Yet, the relatively high prices, and low flexibility of these simulators, are limiting factors that hinder their successful application in the training of laparoscopic surgeons in developing countries such as Colombia.
In the present paper we describe the development of a surgical simulation system to train basics tasks and the cholecystectomy procedure, proposing different algorithms and hardware designs in each of four topics previously described.
III. MATERIALS AND METHODS
In order to simulate a basic surgery environment it is necessary to determine the surgical procedure to be simulated. In the surgical education field a procedure that is frequently used as the first step of training is the cholecystectomy [3]. This procedure is ideal to train the skills in a trainee for the follow reasons:
- The surgeon just needs a basic anatomical and physiologic knowledge of the anatomical structures that take active part in the procedure.
- The procedure allows the manipulation of the organs and tissues using several instrument types. It demands the trainee to become familiar with the surgical instrumental.
- The workspace in which the trainee moves the instruments is not very small when compared with other procedures.
- The step sequence to carry out the procedure is not very complex.
- In the laparoscopic surgery field this procedure is the most frequently executed and improved.
In the next sections we describe the development of each component of the surgical simulator.
3.1 Anatomical Model
All surgical simulators should have an anatomical model of the part seen by the surgeon. In our case, the surgical simulator developed will be composed for two different training environments. The first simulates a basic surgical task such as transport objects using the surgical instruments. The second simulates an environment to execute a basic surgical procedure. In this paper we focus on describing the development of second training environment.
The cholecystectomy is a surgical procedure to extract the gallbladder. The surgeon has to interact with two different organs, the liver and the gallbladder. Still, there are other structures such as a common bile duct, which must be modeled also. This duct plays a main role in the cholecystectomy procedure because it has to be cut and sealed before extracting the gallbladder. For this reason a tridimensional model of the liver, gallbladder and associated structures should be created to develop a simulation of this procedure. In [17] the way how the liver and gallbladder are interconnected with the other structures is described in more detail.
To generate the tridimensional model, we used the images provided by the Visible Human project [18,19]. From these images we carried out a process composed of two stages. The first stage consists of the extraction of the contour from the anatomical structure, i.e. the liver or gallbladder, in each of the images that compose its volume. The second stage consists of a tridimensional reconstruction process using the contours provided by the first stage. Each stage is composed by several processing steps, Fig. 1 shows the complete process.
3.1.1. Contour Extraction
The segmentation methodologies for the extraction of contours of the anatomical structures can be classified on three types of algorithms: the automatic, semi-automatic and manual. Considering the methodologies mentioned above, we have chosen to pick a semi-automatic strategy, which gives us precision and flexibility, with a little user intervention when compared with manual methodologies. Next we will describe the methodology proposed.
Fig. 2 shows the processing steps involved with the methodology proposed to extract the contour. First the user has to select some points, called control points, located over the contour of the organ. Second the application adapts the points defined by the user to the contour, using edge detection methods. Third the application interpolates the points adapted applying the spline cubic method. Fourth if the contour interpolated does not correspond correctly to the contour of the organ because it is very irregular, the application solves it dividing the splines in several segments. Finally, the application applies a floodfill algorithm to define the area delimitated by the contour.
3.1.2 Generation of the Tridimensional Mesh
The methodology proposed to create the tridimensional mesh of the organ is based on the Marching Cubes algorithm. Using the areas determined in the first stage we built a volumetric set of points that describe the volume of the organ. From these points we define a volumetric cell in which if the cell corresponds to a point of the organ, its values is equal to a number different of zero. This volumetric cell is the input of the marching cubes algorithm to create the tridimensional mesh, and it use the number mentioned before as a threshold to calculate the mesh. Additionally, in order to improve the quality of the mesh, we apply decimation and smoothing algorithms after applying the marching cubes [20].
3.2 Soft Tissue Deformation
3.2.1 Mass-Spring Model
We applied the mass-spring method to simulate the deformation of the tissues and organs in the surgical simulator. The soft-tissue simulation engine used a quasi-static solver, which is appropriate for heavily damped tissues, and ignores velocity and damping forces in return for significantly improved performance [8]. In this way we just take the elastic part of the equation that describes the behavior of deformable objects. This simplification results in,
where,
Fij (xi, xj) = kij Δij uij
and
Δij = lij - rlij
In these equations kij is stiffness constant associated with a link between nodes Ni and Nj, Δij is the current length of the link minus its resting length, and uij is the unit vector pointing from nodes Ni toward Nj.
After defining the mathematical model, the next step is to determine the method to solve the equations system. In this system, we have n equations where n is the number of nodes, it correspond a linear system of n equations with n unknown variables. The unknown variables are the positions of each node in the mesh. The application and solution of the model can be observed in the following algorithm:
Acquire the position of the each node
While time < δ then
For each i  I
I
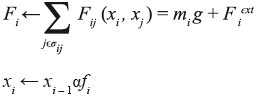
End For
End While
where time is the elapsed time, δ is an interval of time predefined and α is a convergence factor of the solution method. To solve the model, we use the iterative schema proposed in [8].
3.2.2 Boundary Conditions Besides
defining the deformation model and setting out a method to solve it, we have to determine the boundary conditions of the model. These boundary conditions depend on the surgical procedure simulated. Our deformation model have three types of boundary conditions to each node: (i) the first one is a free node, in which the behavior of the node is governed by the equations mentioned before, (ii) the second one is a node subject to an external force, for example when the surgical instrument push an organ or tissue, in this case | Fiext | > 0 and (iii) the third one is a node with a predefined position, for example when a surgical instrument grabs a part of the organ or tissue. In this case the positions of nodes grabbed are equal to the position of the instrument tip.
It is therefore necessary to define the boundary conditions for each particular surgical procedure in order to faithfully reproduce the anatomical conditions of the real environment. In our case the following conditions were defined for the cholecystectomy procedure:
- The nodes located in the anterior and superior diaphragmatic face of the liver are fixed to its rest position due of the contact with the abdominal wall and diaphragm.
- The nodes located in the division of the right lobe and left lobe are fixed due to the action of the falciform ligament.
- The nodes located in the superior diaphragmatic face of the liver are fixed due to the action of coronary ligament.
- The nodes located in the posterior face of the gallbladder are fixed to some nodes of the visceral face of the liver.
For simplification purposes, other boundary conditions of some additional ligaments are not accounted for. Other boundary conditions like the contact with gastric structures are not simulated due to the absence of these structures in the simulation environment.
3.2.3 Shape Conservation
A main characteristic that all physical models should simulate to add realism to the deformation behavior is the volume conservation of the anatomical structures. When we use mass-spring models and surface mesh this property is not guaranteed, even with a volumetric mesh this condition is difficult to satisfy. Recent research has proposed solutions to this problem using the mass-spring model and superficial mesh [21]. However, the proposed methods are computationally expensive. To avoid these problems we propose to add a virtual spring to each node in the mesh. This virtual spring is linked to the rest position of the node before the simulation starts. Although this method does not guarantee the volume conservation of the structure, it guarantees a relative conservation of the shape of the organ, giving some realism to the simulation. Also, the property of the anatomical structure to come back to its rest shape after being exposed to a deformation phenomenon is defined by a stiffness constant of the virtual spring. Fig. 3 shows the configuration of the virtual springs in order to guarantee the preservation of the mesh shape. In the figure kvirtual is the stiffness constant of the springs; pstart is the start position of a node that has not suffered a deformation; and m is the mass associated with each node.
3.2.4 GPU-based Implementation of the Mass-Spring Model
The largest computational task in surgical simulators is that of simulation of the deformation of the anatomical structures. In recent years, the advent of programmable graphical processing unit (GPU), has allowed for the use of the computational power for General-Purpose Computing on the Graphics Processing Unit (GPGPU), such as calculating the deformation of anatomical structures in the surgical simulator [22]. Due to the above reasoning, and the high degree of parallelization possible within the calculation of the mass-spring model, these methods are a perfect candidate to be implemented on the GPU. In this way to get better performance using the processing capacity of the GPU, we explore a GPUbased implementation using the mass-spring model and applying the CUDA (Computed Unified Device Architecture) library. CUDA allows storing the data used in the processing in three different kinds of memory of the graphics device, depending on the memory used the performance of the implementation could be better. In [23] is described and compared the different kinds of memory of the graphic device supported by CUDA. Next we describe the approaches implemented in the GPU to calculate the deformation using four different memory setups in order to store the data structure of the mesh.
- Global Memory Implementation: The data structure used in the GPU implementation consists of three 1D arrays which are linked by the position of each point in the array. The first array called Positions contains the geometric coordinates, the mass and the boundary condition of the each point. The second array called Neighbors has the neighbors of each point in the mesh and the third array called Length Rest contains the length rest of each link in the mesh. In this implementation the data structure is stored in the global memory of the GPU. To decompose the problem each thread in GPU computes the new position of a point in the mesh. For meshes with a large number of points, this approach can offer a great performance improvement, due to the high parallelization achieved in the calculation. However, the use of global memory to store the data structure may limit the performance by this approach due to high latency of reading and writing to global memory on the GPU. To solve this problem, three additional approaches were considered: coalescence memory, shared memory and shared memory + coalescence memory.
- Coalescence Memory Implementation: By performing a simple modification of the data structure described before, it is possible to improve the performance of the algorithm implemented on the GPU. To this end, it is necessary to apply the concept of coalescence memory. Coalesced memory refers to property that the global memory of the GPU has been arranged in a way to allow memory access to the same DRAM (Dynamic Random Access Memory) page when multiple threads simultaneously access contiguous elements of memory [23]. For that reason, and in order to exploit this property of the global memory, the data structure described before was slightly modified, simply by organizing all information that will be accessed at the same time for each thread in a consecutive way in the memory. This schema ensures that the coordinates x, y and z, the masses, boundary conditions, neighbors of each point and the rest length of each spring are consecutively stored in memory.
- Shared Memory Implementation: Other option for improving the performance of the algorithm is to use the shared memory of the GPU, which has writing and reading latency that is less than that of the global memory [23]. The idea of this approach is to copy the positions of points from the global memory to shared memory. Exploiting the characteristics of a neighborhood and in this way to minimize the accesses made to the global memory. However, this is only applicable if the information contained in the array is structured, i.e. if the neighbors of a specific point within the array, are also neighbors in the geometry of the mesh. Changes to the data structure are basically focused on how the neighbors of each point are stored. In this case the index is the position of a point in the array of points. In the new data structure each point has maximum eight neighbors, and to determine if there is a connection with each of these neighbors, values of 0 and 1 are used, where 1 refers to a connection and 0 otherwise. Regarding the changes of the algorithm, each thread of the block reads a point of the mesh and is copied to shared memory, but for the calculation it is necessary to have access to the coordinates of the points around the block some threads of the block must copy these in addition to all positions.
- Shared Memory + Coalescence Memory Implementation: Finally, the last implementation carried out, took advantage of the benefits in terms of performance offered by shared memory and the property of coalescence memory. For this purpose we combined the data structures used in each approach.
In [24] there are more details about the GPU implementation of the mass-spring model using CUDA.
3.3 Collision Detection
Quick collision detection between a rigid object and a deformable object can be implemented applying several techniques, for example, it is possible to compute the distance between two objects applying spatial decomposition using voxels. However, one of the methods currently used in surgical simulation, is based on the use of a hierarchy of bounding volumes of different types, for instance spheres [25], AABB's (Aligned Axis Bounding Boxes) [26], OBB's (Oriented Bounding boxes) [27], among others.
The hierarchy of bounding volumes consists basically in creating a hierarchy of several levels of bounding volumes that cover the object, in our case the liver or the gallbladder. For example, in a binary hierarchy, the first level consists on a coarse bounding volume that contains all the organ, in the second level other two bounding volumes contain half of the organ and so on, until arriving at level n in which the bounding volumes contain the minimum primitive of the mesh, in our case a triangle.
However, in the methods mentioned above, the precision of the outcome depends on the following factors (i) type of bounding volume used, (ii) the adaptation to the object's shape by the bounding volume and (iii) the computational cost of the test performed to detect the collision. The algorithm proposed for the surgical simulator is based on the approximation of the closest of the most distant triangles, it allows to forgetting the overlap and fitting problem of the bounding volumes.
The proposed algorithm is composed by three parts: The first one consists in building the hierarchy. The second one consists in searching for the zone of possible collision between two triangles of different meshes, in our case the mesh of the organ and the mesh of the surgical instrument. The third one consists of updating the hierarchy in order to reflect the deformation suffered by the object when it is exposed to the effect of external forces such as the interaction with other anatomical structures or surgical instruments.
Next we describe the some basic concepts and the three parts of the proposed collision detection method.
3.3.1 Overview of the Algorithm
The triangle is the minimum primitive that can compose the mesh of the objects in the surgical simulator. For simplicity and accuracy purposes, we represent every triangle in the mesh using a point; it is the intersection of the angle bisectors, that is, the center of the triangle's incircle. This point is called the triangle's centroid. For any triangle its centroid will always be located inside it.
In order to describe the algorithm for building, searching and updating the hierarchy, we use the following notation:
- U0 denotes the universe of valid triangle's centroids that compose the organ.
- Ni = | Ui |denotes the size of Ui, which is a subgroup of U0.
- Ci
 Ui and is a centroid point.
Ui and is a centroid point. - Ui and Uk are two subgroups of Ut where Ut is the parent of Ui and Uk, and Ui
 Uk = Ut and Ui
Uk = Ut and Ui  Uk =
Uk =  .
. - The function d:X x X
 R denotes the distance between two points (if the distance is small, the points are close).
R denotes the distance between two points (if the distance is small, the points are close).
3.3.2 Building the Hierarchy
Taking into account the above notation, the proposed algorithm to build the hierarchy is described as follows:
Load Hierarchy (Ut)
If Nt > 1 then
Divide Ut in Uk and Uj
Does Ut father of Uk and Uj
Load Hierarchy (Uk)
Load Hierarchy (Uj)
End if
End Load Hierarchy
In this way to divide Ut in Uk and Uj, the algorithm searches the two point Ck and Cj farthest between in Ut using this definition
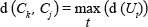
where t is the index of group analyzed in that instant. Based on this criterion, we proceed as follow to define the content of the hierarchy:
For each Ci in Ut - { Ck, Cj }do
If d(Cj , Ci) > d(Ck, Ci) then
Include Ti in Uk
Else If
Include Ti in Uj
End if
End For
3.3.3 Searching in the Hierarchy
After building the hierarchy, we can search the triangles with a possible collision, applying this algorithm:
Search Collision (U0, T)
Usearch = U0
While Usearch > 1 do
If d(T, C1) > d(T, C2)
Usearch = Uk
Else if
Usearch = Uj
End if
End While
Find the triangle Tr refer to Usearch
Find the triangle Tc belong to T
Return if there are collision between Tr and T
End SearchCollision
where Usearch is the group of points where the search is happening and Tr is the triangle reference of the point T.
3.3.4 Updating the Hierarchy
Due to the fact that the proposed hierarchy does not use bounding volumes to detect the collision between objects and it just uses points and calculates the distance to detect the collision, the process of update the hierarchy consist in recalculating the intersection point of the medians of each triangle taking the vertex of the modified triangle. The following algorithm presents the methodology used to update the hierarchy.
Update Hierarchy (Ut)
For each Cj that Cj  ListModified
ListModified
Recalculate Cj
End For
End UpdateHierarchy
Where ListModified is a list with the centroid of the triangles that suffer some deformation. The update approximation is bottom-up, that is, the nodes of the hierarchy are recalculated beginning with the leaf nodes and finalizing with the root node.
3.4 Architecture of the Simulator
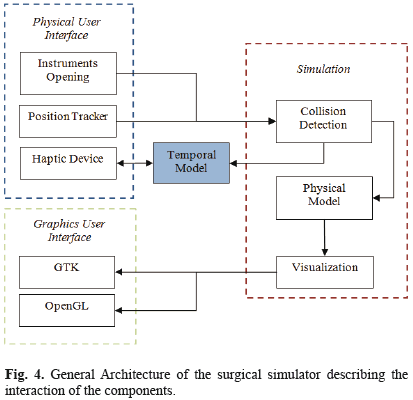
The surgical simulator is a complex system composed by several components that interact amongst them. These components are controlled to achieve the real-time performance necessary to accomplish the requirements of the interactivity with the user. In the Fig. 4 we can observe the global architecture of the surgical simulator developed.
In general, the developed surgical simulator is composed by three components: the physical user interface, the graphical user interface and the simulation core. The first component, the physical user interface is composed by the mechanical device, it allows the movement of the instruments in a way similar to a real surgical procedure, the spatial position tracking device of the surgical instruments, the hardware to measure the opening of the instruments and finally the force feedback devices (Phantom Omni). The interaction between the Phantom Omni and the simulation core is accomplished by the Open Haptics software library, and to grant the real-time performance of the simulator we have to use a temporal model of the virtual object interacting with the user. The temporal model is just a segment of the mesh determined using the collision zone, it includes geometrical and physical information in order to calculate the deformation of the mesh and the force feedback in the segment.
Given that the temporal model contains a reduced subset of the complete mesh, we can achieve the computation of the deformation and the force feedback with an approximate performance of 600 Hz. The second component, the graphical user interface, uses the OpenGL library to visualize the virtual environment and GTK (GIMP Toolkit) to implement a GUI environment to allow the user to interact with menus, buttons and edit textboxes to setup the simulator. The third component, the core simulation, implements the necessary algorithms to detect the collisions between objects in the virtual environment, the implementation of the physical model to calculate the deformation and the visualization module to show the state of the virtual environment.
3.5 Simulator-Surgeon Interface
In a surgical simulator the physical interface plays an important role. The movements of the instruments and the feedback of the different perceptions must be similar to the real life counterparts. This guarantees a correct transfer of the skills from the virtual to the real surgical environment. We analyzed the movements executed by the surgeon during a laparoscopic surgical procedure and found that in a real laparoscopic procedure, instruments have four degrees of freedom, and it is enough to locate the tip of the instrument in the working space.
The physical interface was designed and built to satisfy the mobility requirements of the instruments and to allow adapting the measurement devices such as the haptic devices and the electromagnetic tracker. For this reason, we do not use magnetic materials (metals), since they would distort the electromagnetic field and then the measurement of the instrument position would be incorrect. Fig. 5 shows the physical interface built for the interaction between the user and the surgical virtual environment.
On the other side, the physical interface of the surgical simulator should measure the degrees of freedom of each surgical instrument so that it can be visualized in the surgical simulator. In this way, an electromagnetic Polhemus tracker is adapted to the instruments of the physical interface to measure three degrees of rotation and one of translation. In order to measure the opening of the instruments, we developed a hardware based on a potentiometer link to the handle axis of the instrument. This potentiometer is integrated with a digital-to-analog conversion circuit and a special chip to execute the USB communication with the surgical simulation core.
Finally, there are two haptic devices linked to the tip of the instrument to provide force feedback of the virtual environment to the user.
IV. RESULTS
To evaluate the implemented surgical simulator, we tested the performance of each algorithm proposed in the previous sections. Next we describe the results obtained during each test carried out.
4.1 Experimental Test Collision Detection
The experimental test to evaluate the performance of the search algorithm for collision detection was to take the time required by the algorithm to perform the search and determine the triangle which was in collision with the tip of the instrument, evaluating different mesh sizes. The test was carried out in Dell XPS machine, with 2 GB RAM and processor Intel Core2Duo. In Fig. 6 we can observe the results obtained.
Similarly, the update algorithm was evaluated. In this case we calculated the time that the algorithm took in order to recalculate the centroid of each triangle, and update the farthest points of each of the nodes in the hierarchy. In the Fig. 7 we can observe the results obtained respect to the updated of the hierarchy for meshes of different sizes.
4.2 Experimental Test GPU-based implementation of the Mass-Spring Model
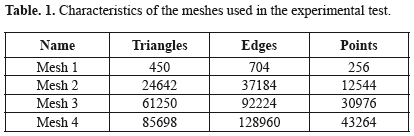
In order to compare the sequential and GPU algorithms proposed for the mass-spring model, an experimental test was developed. In the test two performance variables were measured, time execution and speed-up. The simulation was composed by a triangular mesh. We used four meshes with different sizes (Table 1). In order to conduct the experimental test, a perturbation on the physical model of the mesh, produced by an external force, was applied. For the implementation in the GPU, the tests were conducted using a fixed block size for the different resolution meshes. The experimental test was carried out in a machine with a Nvidia GeForce 8800 GT GPU.
Fig. 8 presents the results of the execution time obtained for each of the approaches described before versus the number of points that possess each of the meshes evaluated.
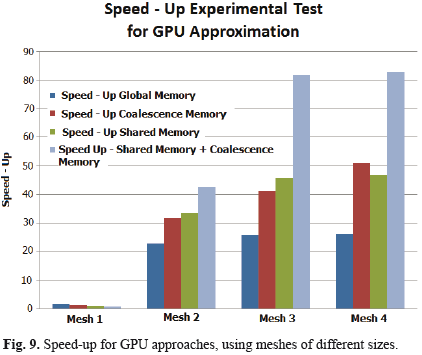
Additionally, Fig. 9 shows the speed-up achieved for each of the approaches and meshes evaluated during the experimental tests.
4.3 Experimental Test Shape Conservation
To evaluate the effectiveness of the proposed method for preserving the shape of objects after they suffered a deformation phenomenon, we made a pilot test in which a mesh suffered a deformation caused by gravity. Evaluating different values of stiffness constant of the virtual springs, were determined the difference between the position of the nodes initially and after have suffered a deformation. The different was calculated using the follow expression:
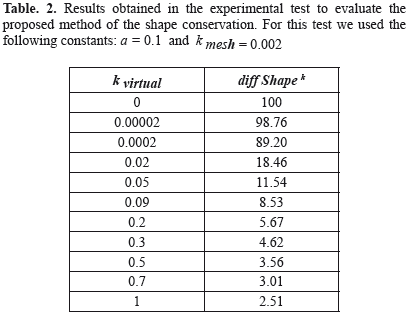
where error0shape refer to the error calculated using k=0. Table 2 shows the results obtained for this experimental test.
4.4 General Performance Test
The developed system simulates a cholecystectomy procedure with an appropriate degree of realism and in real-time. Preliminary tests to analyze the skills transfer of the surgeon lead us to anticipate the success of the surgeon training using this surgical simulator as training tool [20]. Also, the proposed architecture results in a performance of the graphics interface up to 60 Hz and the haptic interface up to 600 Hz. Fig. 10 shows the surgery environment simulated by the system.
On the other side, the preliminary analysis of the physical interface and the anatomical generated model carried out with expert surgeons has given a positive comments about the interaction and the virtual environment of simulation, however we must carry out experimental tests to measure the level of skills transfer achieved with real surgical procedures.
V. DISCUSSION
We faced several challenges during the development of the surgical simulator for a specific procedure as the cholecystectomy; among the most important are the need to guarantee the real-time performance and a suitable realism of the simulation. In order to meet all requirements it is important to develop efficient algorithms in each component of the simulator and to design an architecture that guarantees the real-time at any moment.
The generation of an anatomical model that fulfills the morphologic requirements and additionally facilitates the mapping to the physical model to guarantee the correct behavior of the anatomical structures was a highly complex process. During the extraction of the contours and the tridimensional reconstruction of the anatomical structures using the images of the visible human project, we faced two problems: respect to the complexity of the mesh, that is, the large number of primitives and the stair effect consequence of the inaccuracy of the segmentation method of the contours. These two problems were solved applying decimation and smoothness algorithms of the tridimensional mesh. The size of the meshes generated for the deformable anatomical structures such as the gallbladder (1798 triangles) and the liver (5132 triangles) were suitable for visualization purposes and allowed us to achieve a real-time performance without affecting the realistic anatomical appearance of the structures.
In our case, the collision detection algorithm is simple when compared to the interaction necessary in a surgical simulator. In our approach, we do not detect collision between meshes, but collisions between a triangle and a mesh, that is, the deformable organ is modeled like a mesh but the surgical instrument is modeled using a triangle of its tip. Although there are situations during the simulation where the realism is affected by this simplification, for example when an instrument tube overlaps some organ or tissue, this simplification allowed us to improve the performance of the search and update algorithm in the hierarchy. Observing the figure 6 and figure 7 we can conclude that the search and updating process can be done by ensuring the real-time of the simulation, since the time it takes to execute the two processes for meshes of approximately 4000 triangles, is 3 ms. Also, the use of hierarchies based on distances and not bounding volumes avoids problems related to the adaptation of the bounding volume to the geometrical characteristics of the mesh.
The use of a physical simulation engine concentrated in the local behavior of the organ-instrument interaction, allows for several simplifications to guarantee the realtime performance without affecting the realism of the simulation.
However, for meshes with a large number of nodes such simplifications may not be enough. In this case the benefits of implementing the model mass-spring on the GPU, can ensure real time despite the number of nodes that have the mesh. This result is visible by analyzing figure 9 where the speed-up of the GPU algorithms can be observed. In this case, the higher speed-up was obtained with the implementation on the GPU that combines the use of shared memory and the property of coalescence memory. However, the methods that use shared memory, need a structured mesh to be implemented, this limits the implementation of such methods to only those with a structured mesh. The coalesced memory approach is very flexible since it can represent arbitrary geometry, and is the simplest strategy to be implemented. Moreover, from figure 8 it is possible to conclude that, if it is necessary to simulate the deformation of meshes with up to 43K points for real time applications, the best option is to apply the approaches that use the GPU, since these can provide for a computation time less than 16 ms, and obtain an approximate update frequency of 60 Hz. This frequency guarantees the interactivity of the simulation in a real-time surgical simulator.
Considering the use of virtual springs in the massspring model to conserve the rest shape of the anatomical structures can be an indirect form to conserve volume if there is not a rigid body transformation over the structures. Table 2 shows the effect of the errorkshape when we modified the stiffness constant of the virtual springs, as is expected the error was small when the stiffness constant was big. However if we use a big virtual stiffness constants, we can modify the normal physical behavior of the mesh. In our simulation, applying the quasistatic method solver, considering the size of the organs reconstructed, we achieved the equilibrium of the model in each frame using a α = 0.1 and a δ = 20 ms, with an error below to 0.0005.
On the other side, the design of the physical interface to interact with the virtual environment in laparoscopic surgery procedures impose the fulfillment of the requirements inherent to the application as the mobility of the instrument and technical requirements related with the integration of the haptic feedback and position tracking devices. Special articulated mechanisms had to be designed to fulfill these design criteria. Preliminary user test comparing the use of the interface during the execution of a basic training task have submitted a positive evaluation of the developed interface [20].
Finally, the use of a temporal model to solve the problem of the update rate difference between the haptic and graphic loop guarantee stability in the force perceived by the user.
VI. CONCLUSION
The proposed surgical simulator offers a solution to satisfy every technical requirement demanded for a simulation system; in this case the procedure simulated is the cholecystectomy, providing a suitable visual and haptic feedback to the user. However, the system presented requires additional research in each of the developed components to improve the interactivity and the realism of the simulator.
Future work includes research in four directions specifically. The first one consists in the development of dataset to allow the simulation of anatomical variations and pathologies of the anatomical structures mentioned before. The second one is the study and implementation of an algorithm that allows the volume conservation using mass-spring models and surface mesh, as the proposed in [21]. The third one refer to add algorithms to simulate the cut and application of surgical staples in order to allow the complete interaction of the cholecystectomy procedure, because at the moment the process of cut and location of staples in the simulator is implemented in predefined places affecting the interactivity of the simulator. Finally, we will explore the remote training of surgical procedures developing a networked surgical simulator.
REFERENCES
[1]. Club, S. S. A Prospective Analysis of 1518 Laparoscopic Cholecystectomies. England Journal Medicine, Volume 16, 1991, pp. 1073-1078. [ Links ]
[2]. Tendick, F., Downes, M., Goktekin, T., Cavusoglu, M. C., Feygin D., Wu, X., Eyal, R., Hegarty, M. and Way, L. W. A Virtual Environment Test bed for Training Laparoscopic Surgical Skills, Presence: Teleoperators Virtual Environment. Volume 9, Issue 3, 2000, pp. 236-255. [ Links ]
[3]. Liu, A., Tendick, F., Cleary, K. and Kaufmann, C. A Survey of Surgical Simulation: Applications, Technology, and Education, Presence: Teleoperators Virtual Environment. Volume 12, Issue 6, 2003, pp. 599-614. [ Links ]
[4]. Delingette, H. and Ayache, N. Hepatic Surgery Simulation, Communications ACM, Volume 48, Issue 2, 2005, pp. 31-36. [ Links ]
[5]. Laugier, C., Mendoza, C. and Sudaraj, K. Towards a Realistic Medical Simulator using Virtual Environments and Haptic Interaction. Robotics Research, Volume 6, 2003, pp. 289-306. [ Links ]
[6]. Williams, D., Grimm, S., Coto, E., Roudsari, A. and Hatzakis, H. Volumetric Curved Planar Reformation for Virtual Endoscopy. IEEE Transactions on Visualization and Computer Graphics Volume 14, Issue 1, 2008, pp. 109-119. [ Links ]
[7]. Bayona, S., García, M., Mendoza, C. and Fernández, J. M. Shoulder Arthroscopy Training System with Force Feedback. In: MEDIVIS '06: Proceedings of the International Conference on Medical Information Visualization-Biomedical Visualization, IEEE Computer Society, Washington, DC, USA, 2006, pp. 71-76. [ Links ]
[8]. Brown, J., Sorkin, S., Latombe, J.C., Montgomery, K. and Stephanides, M. Algorithmic Tools for Real-Time Microsurgery Simulation, Medical Image Analysis, Volume 6, Issue 3, 2002, pp. 289-300. [ Links ]
[9]. Raghupathi, L., Grisoni, L., Faure, F., Marchal, D., Cani, M.P. and Chaillou, C. An Intestinal Surgery Simulator: Real-time Collision Processing and Visualization. IEEE Transactions on Visualization and Computer Graphics, Volume 10, Issue 6, 2004, pp. 708-718. [ Links ]
[10]. Wagner, C., Schill, M. and Manner, R. Intraocular Surgery on a Virtual Eye. Communications ACM, Volume 45, Issue 7, 2002, pp. 45-49. [ Links ]
[11]. Meier, U., Lopez, O., Monserrat, C., Juan, M. and Alcaiz, M. Real-time Deformable Models for Surgery Simulation: A Survey. Computer Methods and Programs in Biomedicine, Volume 77, Issue 3, 2005, pp. 183-197. [ Links ]
[12]. Teschner, M., Kimmerle, S., Heidelberger, B., Zachmann, G., Raghupathi, L., Fuhrmann, A., Cani, M., Faure, F., Magnenat-Thalmann, N., Strasser, W. and Volino, P. Collision Detection for Deformable Objects. In: Eurographics State-of-the-Art Report (EG-STAR), Eurographics Association, 2004, pp. 119-139. [ Links ]
[13]. Brown, J., Latombe, J.C. and Montgomery K. Real-Time Knot-Tying Simulation. Visualization and Computer, Volume 20, Issue 2, 2004, pp. 165-179. [ Links ]
[14]. Salleh, R., Razak, Z., Caldwell, D. and Loureiro, R. Salfsar: A Dual Purpose Device for Laparoscopic Training and Tele-surgery. Malaysian Journal of Computer Science, Volume 18, Issue 1, 2005, pp. 78-92. [ Links ]
[15]. Webster, R., Haluck, R. S., Zoppetti, G., Benson, A., Boyd, J., Charles, N., Reeser, J. and Sampson, S. A Haptic Surgical Simulator for Laparoscopic Cholecystectomy using Real-Time Deformable Organs. In: Proceedings of the IASTED International Conference Biomedical Engineering, IASTED Press, 2003. [ Links ]
[16]. Schijven, M. and Jakimowicz, J. Virtual Reality Surgical Laparoscopic Simulators. Surgical Endoscopy, Volume 17, Issue 12, 2003, pp. 2041-2042. [ Links ]
[17]. Gunn, C. Using Haptics in a Networked Inmersive 3D Environment. Ph.D. Thesis, 2007. (Chapter 8 and 9). [ Links ]
[18]. Ackerman, M. and Banvard, R. Imaging Outcomes from the National Library of Medicine's Visible Human Project. Computerized Medical Imaging and Graphics, Volume 24, Issue 3, 2000, pp. 125-126. [ Links ]
[19]. Juanes, J., Prats, A., Lagndar, M. and Riesco, J. Application of the Visible Human Project in the Field of Anatomy: A Review. European Journal of Anatomy, Volume 7, Issue 3, 2003, pp. 147-159. [ Links ]
[20]. Diaz, C., Posada, D., Trefftz, H. and Bernal, J. Development of a Surgical Simulator to Training Laparoscopic Procedures. International Journal of Education and Information Technologies, Volume 2, Issue 1, 2008, pp. 95-103. [ Links ]
[21]. Hong, M., Jung, S., Choi, M.H. and Welch, S. W. J. Fast Volume Preservation for a Mass-Spring System. IEEE Computer and Graphics Applications, Volume 26, Issue 5, 2006, pp. 83-91. [ Links ]
[22]. Sorensen, T. S. and Mosegaard, J. An Introduction to GPU Accelerated Surgical Simulation. In: M. Harders, G. Szekely (Eds.), Third International Symposium, ISBMS 2006, Vol. 4072 of Lecture Notes in Computer Science, Springer Berlin / Heidelberg, 2006, pp. 93-104. [ Links ]
[23]. Hwu, W.-M., Rodrigues, C., Ryoo, S. and Stratton, J. Compute Unified Device Architecture Application Suitability. In: Computing in Science and Engineering, Volume 11, Issue 3, 2009, pp. 16-26. [ Links ]
[24]. Diaz, C., Eliuk, S., Trefftz, H. and Boulanger, P. Simulating Soft Tissue using GPU approach of the Mass-Spring Model. In 3IA '2010 International Conference on Computer Graphics and Artificial Intelligence 2010. [ Links ]
[25]. Hubbard, P. M. Approximating Polyhedra with Spheres for Time-Critical Collision Detection. In: ACM Transactions Graphics, Volume 15, Issue 3, 1996, pp. 179-210. [ Links ]
[26]. Zhang X. and Kim, Y. J. Interactive Collision Detection for Deformable Models using Streaming AABB's. In: IEEE Transactions on Visualization and Computer Graphics, Volume 13, Issue 2, 2007, pp. 318-329. [ Links ]
[27]. Gottschalk, S., Lin, M. C., Manocha, D. OBBTree: A Hierarchical Structure for Rapid Interference Detection. In: SIGGRAPH '96: Proceedings of the 23rd Annual Conference on Computer Graphics and Interactive Techniques, ACM, New York, NY, USA, 1996, pp. 171-180. [ Links ]