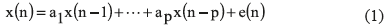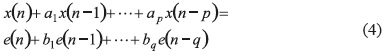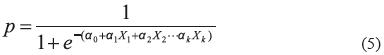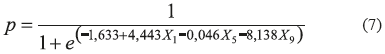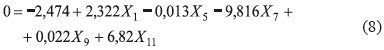Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
Revista Ingeniería Biomédica
versão impressa ISSN 1909-9762
Rev. ing. biomed. vol.5 no.9 Medellín jan./jun. 2011
ANÁLISIS Y CLASIFICACIÓN DEL PATRÓN RESPIRATORIO DE PACIENTES EN PROCESO DE RETIRADA DEL VENTILADOR MECÁNICO
ANALYSIS AND CLASSIFICATION OF THE BREATHING PATTERN IN PATIENTS ON WEANING TRIAL PROCESS
Javier Alberto Chaparro Preciado1, Beatriz Giraldo Giraldo2
1 Grupo de Investigación BIOECI, Escuela Colombiana de Ingeniería Julio Garavito, Bogotá, Colombia. javier.chaparro@escuelaing.edu.co.
2 Departamento de Ingeniería de Sistemas, Automática e Informática Industrial ESAII, Universidad Politécnica de Cataluña, Barcelona, España.
Recibido 2 de mayo de 2011. Aceptado 29 de junio de 2011
RESUMEN
La estimación del momento óptimo de retirar la ventilación asistida de un paciente en cuidado intensivo sigue siendo fundamental en la práctica clínica. En este trabajo se estudia el patrón respiratorio a partir de la señal de flujo respiratorio de pacientes en proceso de extubación teniendo en cuenta las siguientes etapas: caracterización de la señal a partir de la identificación de los ciclos respiratorios, análisis del patrón respiratorio a partir del modelado matemático de las series, y clasificación del mismo con el objetivo de identificar patrones de pacientes con posible éxito en el proceso. Se analizaron 153 pacientes clasificados en los grupos éxito, fracaso y reintubados, de acuerdo con el resultado de la prueba de extubación de tubo en T. Se seleccionaron las series temporales de tiempo de espiración, tiempo de inspiración, duración del ciclo respiratorio e índice de respiración superficial dado que presentaron diferencias significativas en los parámetros de valor medio, orden del modelo, primer coeficiente y error final de predicción. Con ellas se obtuvo una exactitud de clasificación del 86% (sensibilidad 0,86 - especificidad 0,84) utilizando un clasificador tipo discrimante lineal. Se analizaron otros clasificadores como regresión logística y máquinas de soporte vectorial.
PALABRAS CLAVE: Patrón respiratorio, Ventilación mecánica, Modelado de señal, Retirada del ventilador.
ABSTRACT
Estimating the optimal time to remove the ventilatory support from a patient in intensive care remains essential in clinical practice. In this work we study the breathing pattern from the respiratory flow signal in the process of weaning considering the following stages: characterization of the signal from the identification of respiratory cycles, respiratory pattern analysis from mathematical modeling of the resulting series, and classification in order to identify patterns of patients with possible success in the process. We analyzed 153 patients classified into three groups: success, failure and reintubated, according to results of T-tube test. The time series for breathing duration, inspiratory time, expiratory time, and shallow breathing index that resulted in significant differences in the mean, model order, first coefficient and final error of prediction were selected. With them we obtained a classification accuracy of 86% (sensitivity 0.84 - specificity 0.86) using a linear classifier discriminate type. Other classifications were analyzed, such as logistic regression and support vector machines.
KEY WORDS: Breathing pattern, Mechanical ventilation, Signal modeling, Weaning process.
I. INTRODUCCIÓN
La función principal del sistema respiratorio es mantener la concentración de gases, oxígeno y dióxido de carbono en unos rangos que garanticen el estado homeostático del cuerpo humano. La ventilación es la primera de cuatro fases y una de las más importantes en este proceso, su fallo motiva el ingreso del paciente a una unidad de cuidados intensivos y la instauración de la ventilación asistida mediante un ventilador mecánico. La dinámica de esta primera fase se puede registrar y analizar a partir de señales de flujo, gases, volúmenes o electromiográficas principalmente [1].
La ventilación mecánica es el tratamiento utilizado para suplir la falta de la ventilación espontánea, sin embargo conlleva el desafío clínico de establecer el momento óptimo de iniciar el proceso de extubación. La bibliografía reporta evidencias de una relación directamente proporcional entre el tiempo de conexión al ventilador y el grado de complicación que pueden presentar los pacientes al iniciar su retirada. Los modos de ventilación y los métodos utilizados para la extubación son motivos de diferentes estudios. Se reporta en varios trabajos que hasta un 25% de los pacientes que se desconectan de la ventilación mecánica sufren distrés respiratorio y deben ser reintubados [2-4].
En diversos trabajos se ha analizado el patrón respiratorio de pacientes en proceso de extubación. Se han evaluado diferentes técnicas de procesamiento lineal y no lineal de señales con el propósito de establecer diferencias entre el patrón de pacientes con éxito y fracaso en dicho proceso [5-7]. En este trabajo se presentan los resultados de la caracterización y análisis de las señales de flujo respiratorio de un grupo de pacientes en proceso de weaning mediante técnicas de procesamiento lineal y no lineal. Al final del mismo se identifican las características, obtenidas de las diferentes técnicas de procesamiento, con mayores diferencias significativas que permitieron obtener clasificadores con tasas de acierto superiores al 86%.
La base de datos utilizada está formada por 153 registros de señal de flujo respiratorio de pacientes en proceso de extubación clasificados de acuerdo al resultado del mismo en éxito (E), fracaso (F) o reintubados (R). El trabajo se desarrolló en tres etapas: una primera etapa fue la caracterización de la señal respiratoria mediante un grupo de series temporales obtenidas a partir de la marcación de los instantes de inicio de inspiración y de espiración. Se propuso un algoritmo de marcación basado en la identificación y validación de los cruces por cero. La validación se logró evaluando dos condiciones de flujo y tiempo que debe cumplir la señal después de identificarse el cruce. Como resultado de esta etapa se obtuvieron las series temporales tiempo de inspiración (TI), tiempo de espiración (TE), duración del ciclo respiratorio (TTot), volumen tidal (VT), fracción inspiratoria (TI/TTot), flujo inspirado medio (VT/TI), y el índice de respiración superficial (f/VT), siendo f la frecuencia respiratoria.
En la segunda etapa se realizó el análisis del patrón respiratorio. Se aplicaron técnicas estadísticas y de modelado matemático a las series temporales en los tres grupos de estudio. De las primeras se obtuvieron las variables media, desviación estándar, curtosis, asimetría, distancia intercuartil y el coeficiente de variación. Los modelos utilizados fueron de tipo autorregresivo puro (AR) y autorregresivo de promedio móvil (ARMA). Las variables establecidas en estos últimos fueron el orden (utilizando el criterio de Akaike [8]), el primer coeficiente y el error final de predicción (FPE). Con estas variables se buscaron diferencias estadísticamente significativas entre los grupos E, F y R, aplicando la prueba no paramétrica de Kruskal-Wallis [9].
La última etapa fue la de clasificación en la cual se utilizaron técnicas de regresión logística, discriminante lineal y máquinas de soporte vectorial (SVM). Seleccionadas las quince primeras variables con las mejores diferencias significativas y evaluadas todas las posibles combinaciones con las tres técnicas de clasificación se encontraron tasas de aciertos de 0,87 con la función logística, 0,86 con la función discriminante lineal y 0,87 con las SVM en pacientes en proceso de extubación entre los grupos éxito y fracaso. El grupo de pacientes reintubados fue evaluado con cada una de estas funciones de clasificación y los resultados mostraron que su comportamiento es más cercano al grupo de éxito que al de fracaso.
II. MATERIALES Y MÉTODOS
2.1. Base de datos
El estudio se realizó con la base de datos denominada WEANDB, formada por señales respiratorias de pacientes conectados al ventilador mecánico mediante un tubo endotraqueal. A partir del resultado del test de tubo en T, los pacientes fueron clasificados en tres grupos: grupo éxito (E) con 94 pacientes que superaron satisfactoriamente la prueba y recuperaron la respiración espontánea; grupo fracaso (F) con 38 pacientes que no superaron el test y fueron reconectados al ventilador; y grupo reintubados (R) con 21 pacientes que superaron la prueba y fueron extubados, pero antes de 48 horas fueron reconectados al ventilador. Estos pacientes fueron registrados en los Departamentos de Cuidados Intensivos del Hospital de la Santa Creu i Sant Pau, Barcelona, y del Hospital de Getafe, España, de acuerdo con los protocolos aprobados por sus comités éticos. La señal de flujo respiratorio se obtuvo mediante un pneumotacógrafo (monitor datex-Ohmeda transductor de reluctancia variable) conectado a un tubo endotraqueal. Se registraron 30 minutos a una frecuencia de muestreo de 250 Hz (tarjeta de adquisición National Instruments dAQCard 6024E).
2.2. Caracterización del patrón respiratorio
En la etapa de caracterización de la señal respiratoria se hizo un preprocesado de las señales para acondicionarlas al estudio, que incluía remover los posibles valores espurios. El filtrado pasabajos (0 - 10Hz) de las señales permitió suavizar su trazado, facilitando de esta forma la marcación de los puntos significativos para la estimación de las series temporales. Estos puntos significativos (Fig. 1), o instantes de inicio de inspiración e inicio de espiración, fueron identificados sobre los trazados de flujo respiratorio utilizando un algoritmo de marcación que permitió hacer automático dicho proceso.
El algoritmo procesa una a una las muestras de la señal de flujo. Inicia con la búsqueda de un cruce por cero, si este se presenta, se continua con la detección de la fase respiratoria, una vez conocida la fase de la señal, se evalúan las condiciones de nivel mínimo de flujo y de duración para que el cruce por cero se convierta en un inicio de inspiración o espiración. Las referencias Fsp y Fin son los niveles de flujo mínimo inspiratorio y espiratorio respectivamente; si el flujo está en la fase inspiratoria y supera la referencia Fsp durante un tiempo mayor a Tsp, se marca el último cruce por cero como un inicio de inspiración, de lo contrario, si el flujo está en la fase de espiración y supera la referencia Fin durante un tiempo mayor a Tin se dice que el último cruce por cero corresponde a un inicio de una espiración. Los valores de las condiciones de flujo ascendente Fsp y descendente Fin se establecieron cercanos al 10% del valor máximo inspiratorio y espiratorio respectivamente, previa inspección visual del trazado de la señal. Para las condiciones de duración de tiempo Tsp y Tin se propusieron los valores de 0,1 s.
2.3. Análisis del patrón respiratorio
Un primer análisis se hizo mediante la comparación de los estadísticos media, desviación estándar, curtosis, asimetría, distancia intercuartil y el coeficiente de variación de las series temporales TI, TE, TTot, VT, TI/TTot, VT/TI, y f/VT, entre los tres grupos de pacientes estudiados. Posteriormente se procedió a estimar los modelos autorregresivos puros (AR) y de media móvil (ARMA) a cada una de estas mismas series y analizar sus principales parámetros.
El modelo autorregresivo AR permite establecer la muestra x(n) en función del historial de la misma más un componente de error, como se muestra en (1).
donde p es el orden del modelo estimado mediante el criterio de Akaike, a1,...,ap son los coeficientes reales del modelo, y e(n) es un proceso aleatorio gausiano con media cero y varianza σ2w. Se asume que la secuencia x(n) es de media y varianza ergódica [10]. Otra variable utilizada a partir del modelado de la señal fue el error final de predicción del modelo (FPE), en este se busca minimizar la función (2).
siendo p el orden del modelo, N el número de datos, y s2p el total del error cuadrático dividido por N dado por la relación (3) [11]:
El modelo autorregresivo puro permite establecer la muestra x(n) en función del historial de la misma más un componente de error. Sin embargo, también pueden considerarse componentes móviles que caractericen mejor la dinámica de la serie estudiada. Este es el caso de los modelos ARMA que se pueden describir de acuerdo con la ecuación (4).
donde p y q son los órdenes del proceso estimado mediante el criterio de Akaike, a1,...,ap y b1,...,bq son los coeficientes reales del proceso [12]. El error final de predicción FPE para este tipo de modelo se calcula de acuerdo a la expresión de (2) y (3).
Para cada una de las series temporales de los tres grupos de estudio se obtuvieron las siguientes variables después de estimar los modelos AR y ARMA: orden del modelo, primer coeficiente y error final de predicción. Con estas tres variables se buscaron diferencias estadísticamente significativas entre los grupos E, F y R, aplicando la prueba no paramétrica de Kruskal-Wallis [13].
2.4. Clasificación del patrón respiratorio
En la tercera etapa del trabajo, se seleccionaron las variables que caracterizaron el patrón respiratorio con las mejores diferencias significativas entre los grupos de E y F, y con ellas se evaluaron tres métodos de clasificación: regresión logística, discriminante lineal y máquinas de soporte vectorial. El propósito fue el de obtener una función que clasificara entre estos dos grupos. En el proceso de entrenamiento y validación de los diferentes clasificadores se utilizó la técnica de cross-validation.
Un modelo de regresión con una variable dependiente binomial es un modelo que permite estudiar si dicha variable discreta, depende o no de otra u otras variables. Si la variable binomial de parámetro p es independiente de otra variable X, se cumple (p|X=x)=p, para cualquier valor x de la variable X. Un modelo de regresión logística de k variables se expresa como en (5). El cálculo de los coeficientes α en (5) se puede encontrar en textos especializados [14,15].
De otro lado, la técnica de discriminante lineal permite asignar un individuo a un grupo definido a priori en función de una serie de características del mismo. Una función discriminante es una combinación lineal de las variables independientes. Asumiendo que se dispone de un conjunto de k variables independientes (X1, X2,..., Xk), la función discriminante puede expresarse como en (6).
siendo Xi la i-ésima variable independiente, uo el término independiente, y ui el conjunto de coeficientes de la función discriminante [16].
La teoría de máquinas de soporte vectorial (SVM) está basada en la idea de minimización de riesgo estructural. Una SVM mapea los puntos de entrada a un espacio de características de una dimensión mayor y encuentra un hiperplano que los separa maximizando el margen m entre las clases de este nuevo espacio. La transformación de los datos a este nuevo hiperplano se hace a través de kernels de tipo lineal, cuadrático, polinomial, de funciones gausinas radiales, entre otros. Una explicación detallada del método se puede encontrar en libros especializados [17,18].
III. RESULTADOS
En la caracterización del patrón respiratorio se desarrolló un algoritmo de marcación de puntos significativos con buenos resultados de acuerdo con el proceso de validación realizado con la ayuda de dos médicos expertos. Las distancias euclidianas entre las marcas hechas por los médicos y las hechas por el algoritmo de marcación fueron de 0,04 y 0,01. Estos resultados permiten suponer una buena calidad en las marcaciones. La elaboración de las series temporales TI, TE, TTot, VT, TI/TTot, VT/TI y f/VT se realizó teniendo como punto de partida la estimación hecha de los instantes de inicio de inspiración y espiración.
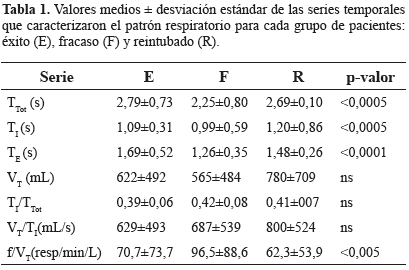
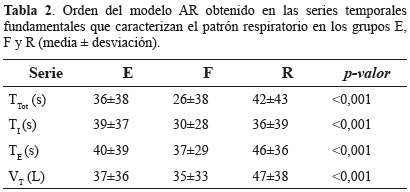
El análisis del patrón respiratorio mostró diferencias significativas entre los grupos E, F y R para los valores medios de las series temporales de duración del ciclo respiratorio, tiempo de inspiración, tiempo de espiración y el índice de respiración superficial. La Tabla 1 presenta estos resultados. Las series temporales de volumen tidal, fracción inspiratoria y relación VT/TI no presentaron diferencias significativas.
Las series temporales que caracterizan el patrón respiratorio presentan comportamientos estadísticos que concuerdan con los reportados en otros trabajos de investigación sobre esta temática y a algunos índices clínicos de extubación ampliamente conocidos. Este es el caso del índice de ventilación superficial (f/VT) el cual predice un éxito si es menor a 80 o un fracaso si es mayor a 100, y los resultados obtenidos para la base de datos WEANDB en los grupos de éxito y fracaso así lo demuestran; sin embargo el grupo de pacientes clasificados como reintubados presenta un índice promedio de 62 lo que llevaría a pensar que son pacientes con un eventual éxito en el proceso de extubación.
Las diferencias estadísticas más importantes fueron obtenidas para los valores medios de las series temporales tiempo de inspiración (TI), tiempo de espiración (TE) y duración del ciclo respiratorio (TTot). La diferencia en la duración del ciclo respiratorio entre los grupos de éxito y fracaso lleva a pensar que una alta frecuencia respiratoria (el inverso del TTot) es indicador de un fracaso en el proceso de extubación. Sin embargo no existen umbrales, en términos de frecuencia respiratoria o duración del ciclo respiratorio, que permitan diferenciar con claridad el grupo de éxito y fracaso; actualmente se recomienda clínicamente que la frecuencia respiratoria deba estar entre 10 y 35 respiraciones por minuto.
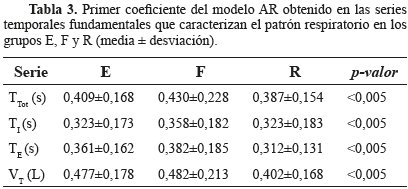
Los modelos autorregresivos puros (AR) aplicados a las series fundamentales del patrón respiratorio (TTot, TE, TI, VT) permitieron establecer que tanto el orden (p) del modelo como el primer coeficiente presentan diferencias significativas en los tres grupos de pacientes (Tablas 2 y 3). Teniendo en cuenta que una señal determinística tiene un orden (p) menor al que tendría una señal aleatoria y que el primer coeficiente del modelo presenta un comportamiento inverso, se puede deducir que las series temporales fundamentales del grupo E presentan una mayor variabilidad en relación con las del grupo F.
Los resultados también muestran que los valores medios del orden p del modelo ARMA estimado en las series temporales TTot, TI y TE tienen la tendencia a ser mayores en el grupo E respecto al grupo F; la diferencia significativa más importante se obtuvo para el tiempo de espiración (p = 0,02). Al comparar el grupo R no se pudieron establecer diferencias o tendencias con respecto a los otros dos grupos. El orden de modelo q estimado para las series temporales TI, TE y TTot fue mayor en el grupo E que el encontrado en el grupo F, siendo VT la serie con mayor discriminación entre los grupos (p = 0,01).
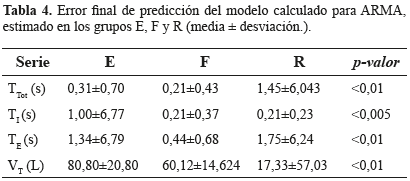
Otra variable que permitió identificar los grupos de estudio a partir de los modelos ARMA es el FPE (Tabla 4). Las series temporales TI, TE, TTot y VT son siempre mayores en el grupo E. Estos resultados, sumados al hecho que el orden promedio de p tiende a ser mayor en el grupo de éxito, sugieren nuevamente una mayor variabilidad en las series temporales de este grupo.
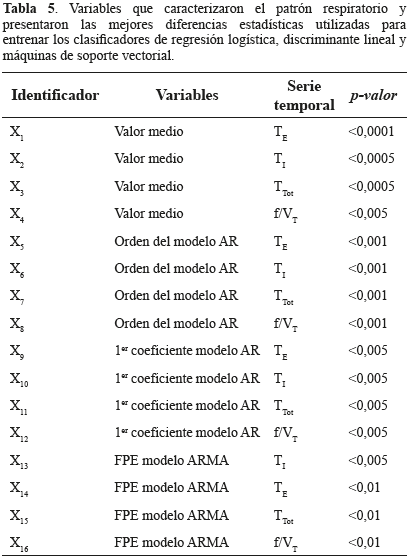
La tercera fase del trabajo se inició con la identificación de las variables que mejores diferencias significativas arrojaban entre los grupos E, F y R. La Tabla 5 recoge las primeras 15 variables estadísticamente significativas según los resultados de la prueba de Kruskal-Wallis. Para facilitar la lectura de las ecuaciones a cada una de ellas se le asignó un identificador entre X1 y X15.
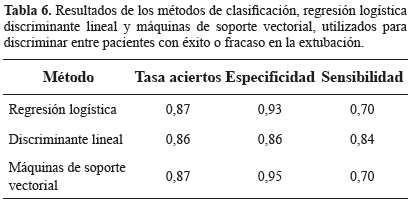
Utilizando el grupo de variables de la Tabla 5 se elaboraron las funciones de clasificación con los métodos de regresión logística, discriminante lineal y máquinas de soporte vectorial que permitieran clasificar el patrón respiratorio de pacientes con éxito o fracaso en proceso de extubación. Se evaluaron todas las posibles combinaciones de las variables para los tres métodos y los resultados con las mejores tasas de clasificación, especificidad y sensibilidad se presentan en la Tabla 6.
La función de regresión logística (7) con la mejor tasa de clasificación (87%) se logró con las variables tiempo de espiración TE(X1), orden del modelo AR del TE(X5) y primer coeficiente del modelo AR del TE(X9). La sensibilidad y especificad obtenida con este clasificador fue de 0,93 y 0,7 respectivamente.
La función discriminante lineal (8) con mejor tasa de clasificación (86%), combinó las variables tiempo de espiración TE(X1), orden p del modelo AR para las series TE(X5) y TTot(X7) y primer coeficiente del modelo para estas mismas series temporales (X9 y X11 respectivamente). Con esta combinación de variables se logró una sensibilidad de 0,84 y una especificidad de 0,84.
Los resultados obtenidos con las máquinas de soporte vectorial mostraron una tasa de aciertos del 86% con una especificidad de 0,95 y una sensibilidad de 0,70 utilizando un kernel lineal.
IV. CONCLUSIÓN
Para la caracterización de la señal respiratoria se propuso un algoritmo que permitió identificar y marcas los instantes de inicio de inspiración y espiración. Con dicho algoritmo se hicieron las marcaciones de las señales respiratorias de la base de datos WEANDB y posteriormente se elaboraron las series temporales que caracterizaron el patrón respiratorio en este trabajo.
Al analizar la base de datos WEANDB se encontraron diferencias significativas entre los valores medios de TI, TE y TTot cuando se compararon los grupos de éxito y fracaso (p<0,005). Cuando se compararon los tres grupos simultáneamente se encontraron diferencias en el rango intercuartil entre las series TE y TTot y la asimetría de TI/TTot. El coeficiente de variación presentó un valor más elevado en las series correspondientes al grupo de éxito que al grupo de fracaso. Este resultado se puede asociar con una mayor variabilidad del patrón respiratorio en los pacientes del grupo éxito respecto a los pacientes de los otros dos grupos.
Con los modelos autorregresivos AR, las variables orden p y primer coeficiente del modelo permitieron caracterizar el patrón respiratorio en los tres grupos de pacientes. Se encontraron diferencias estadísticamente significativas en las series temporales fundamentales TI, TE, TTot y VT. Los modelos ARMA presentaron diferencias en este mismo grupo de series, en el error final de predicción FPE y en la tendencia de los órdenes del modelo p y q en las series fundamentales a ser mayores en el grupo E en relación con el grupo F. Estos resultados sugieren una mayor variabilidad en las series del grupo E teniendo en cuenta que en una señal entre mayor sea su contenido aleatorio mayor es el orden necesario de un modelo autorregresivo y también mayor el FPE del mismo.
Los tres métodos de clasificación utilizados presentaron buenos resultados, con un número reducido de variables. Con el análisis discriminante lineal se obtuvo el mejor compromiso entre sensibilidad y especificidad de la clasificación. Después de evaluar el grupo de pacientes reintubados con estos tres clasificadores, se encontró que estos tienen un comportamiento más cercano al grupo de éxito que al de fracaso. La regresión logística clasificó el 91,6% como éxito, el discriminante lineal el 52% y la máquina de soporte vectorial el 75,1%.
AGRADECIMIENTO
Este trabajo ha sido financiado parcialmente por las ayudas TEC2007-68076-C02-01 y TEC2007-63637 del Ministerio de Ciencia e Innovación del Gobierno de España.
REFERENCIAS
[1]. Guyton A.C., Hall J.E. Tratado de Fisiología Médica. McGraw-Hill, 2001. Capítulo 37 417-437. [ Links ]
[2]. Tobin M. J. Advances in mechanical ventilation, N. Engl. J. Med., 344, 1986-1996, 2001. [ Links ]
[3]. Giraldo B.F., Chaparro J., López-Rodríguez D., Great D., Benito S., Caminal P. Study of the respiratory pattern variability in patients during weaning trials, Memorias de la 26th Conferencia Anual de la IEEE-EMBS. San Francisco, EEUU, 2004. [ Links ]
[4]. Casaseca de la Higuera P., Martin M., Arbeloa C. Weaning from mechanical ventilation: a retrospective analysis leading to a multimodal perspective, IEEE Transaction on biomedical engineering, 53(7), July 2006. [ Links ]
[5]. Giraldo B.F., Chaparro J., Benito S., Caminal P. Effect of pressure support ventilation on the respiratory pattern variability. Memorias de la 25th Conferencia Anual de la IEEE-EMBS. Cancún, México, 2003. [ Links ]
[6]. Giraldo B., Garde A., Arizmendi C., Jane R. , Benito S., Diaz I., Ballesteros D. Support Vector Machine Classification Applied on Weaning Trials Patients. Memorias de la 28th Conferencia Anual de la IEEE-EMBS. New York, EEUU, 2006. [ Links ]
[7]. Hao-Yung Y., Jiin-Chyr H., Yung-Fu C., Xiaoyi J., Chen T. Using support vector machine to construct a predictive model for clinical decision-making of ventilation weaning. Memorias del Congreso Mundial de Computación Inteligente. Hong Kong, 2008. [ Links ]
[8]. Tong H. Autoregressive model fitting with noisy data by Akaike's information criterion. IEEE Transaction on Information Theory. Vol. 21, No. 4, July 1975. [ Links ]
[9]. Witter R., Witte J. Statistics, Wyle, novena edición, 2009, 449-469, 2009. [ Links ]
[10]. Khorshidi Sh., Karimi M. Modified AIC and FPE criteria for autorregresive (AR) model order selection by using LSFB estimation method, Memorias de la Conferencia Internacional sobre avances en herramientas computacionales para aplicaciones en ingeniería. ACTEA'09. Beirut, Líbano, 2009. [ Links ]
[11]. Rahim H., Ibrahim F. Model Order Selection Criterion for Monitoring Hemoglobin Status in Dengue Patients using ARX model, Memorias de la Conferencia Internacional en Tecnología de la Información aplicada en Biomedicina ITAB'08. Shenzhen, China, 2008. [ Links ]
[12]. Box G., Jenkins G., Reinsel G. Time Series Analysis, Forecasting and Control. Tercera edición, Prentice Hall International, 1994. Capítulo 3, 69-77. [ Links ]
[13]. Spiegel M., Stephens L. Estadística. Tercera Edición, Mc Graw Hill, 2001. Capítulo 17. [ Links ]
[14]. Jhonson R., Wicher D. Applied Multivariate Statistical Analysis. Quinta Edición, Editorial Prentice Hall Hispanoamericana. 2006. Capítulo 7. [ Links ]
[15]. Hair J., Anderson R., Tatham R., Black W. Análisis Multivariado de Datos. Quinta Edición, 1999. Capítulo 7. [ Links ]
[16]. Huberty C. Applied Discriminant Analysis. Whiley Series in Probability and Mathematical Statistics, Jhon Wiley & Sons, 1994. Capítulo 4, 53-74. [ Links ]
[17]. Steinwart I., Chrismann A. Super Vector Machine, Information Science and Statistics. Springer, 2008. Capítulo 8, 287-330. [ Links ]
[18]. Burges C. A tutorial on support vector machines for pattern recognition. Data Mining and Knowledge Discovery, 2, 121-167, 1998. [ Links ]