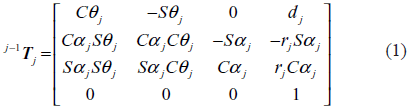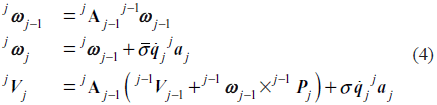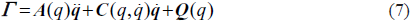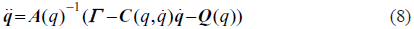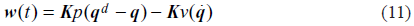Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Ingeniería Biomédica
Print version ISSN 1909-9762
Rev. ing. biomed. vol.5 no.10 Medellín July/Dec. 2011
MODELADO Y SIMULACIÓN DE UN ROBOT PARA CIRUGÍA ENDOSCÓPICA TRANSLUMINAL
MODELING AND SIMULATION OF A ROBOT FOR ENDOSCOPIC TRANSLUMENAL SURGERY
Víctor Hugo Mosquera Leyton1, Oscar Andrés Vivas Albán1,2, Carlos Felipe Rengifo Rodas1
1 Facultad de Ingeniería Electrónica y Telecomunicaciones, Universidad del Cauca, Popayán, Colombia.
2 Dirección de correspondencia: avivas@unicauca.edu.co.
Recibido 27 de enero 2012. Aprobado 17 de febrero 2012
RESUMEN
Este artículo presenta el diseño de un nuevo robot para cirugía endoscópica transluminal. Este tipo de cirugía, evolución tecnológica de la cirugía laparoscópica, pretende ingresar al abdomen del paciente por los orificios naturales (boca, uretra, ano o vagina), y desde allí acceder al sitio donde se hace necesaria la intervención, procedimiento que conlleva muchas más ventajas respecto a la cirugía laparoscópica. El robot diseñado consta de diecinueve grados de libertad y es movido por un joystick utilizando un controlador por par calculado. La simulación muestra bajos errores cartesianos y movimientos muy precisos del órgano terminal.
PALABRAS CLAVE: Cirugía Mínimamente Invasiva, Cirugía Endoscópica Transluminal, Control de Robots, Robótica Quirúrgica.
ABSTRACT
This article presents the design of a new robot for translumenal endoscopic surgery. This type of surgery, evolved from laparoscopic surgery, allows the access into the abdominal cavity of the patient through natural orifices such as the mouth, urethra, anus or vagina, and from there reaches the area of the surgical intervention. This procedure has many advantages over laparoscopic surgery. The designed robot has nineteen degrees of freedom and is moved with a joystick device and controlled by a computer torque control. Simulation shows low cartesian errors as well as accurate movements at the end effector.
KEY WORDS: Control of Robots, Minimally Invasive Surgery, Surgical Robotics, Translumenal Endoscopic Surgery.
I. INTRODUCCIÓN
Afinales del siglo pasado la cirugía laparoscópica instauró una revolución en los quirófanos del mundo, a partir de los trabajos de Mühe [1] y Mouret [2]. Esta técnica realizada en el abdomen del paciente, significó un avance importante respecto a la cirugía abierta convencional. La laparoscopia consiste en la apertura mínima de tres orificios en el abdomen, el primero de los cuales le insufla gas carbónico con el fin de disponer de mayor espacio de trabajo, y luego por este orificio es introducido un endoscopio o mini cámara con su respectiva fuente de luz fría. Los otros dos orificios (o tres en algunos casos) son utilizados para introducir los instrumentos quirúrgicos que manejará el cirujano, el cual podrá observar en un monitor las imágenes del interior del paciente y realizar la intervención programada de acuerdo a ellas.
Las ventajas de la laparoscopia son claras ya que el riesgo de complicaciones e infecciones disminuye considerablemente, la recuperación es mucho más rápida lo cual le conviene al sistema de salud, aparte de los beneficios estéticos generados con la presencia de cicatrices más pequeñas. Entre los procedimientos más comunes realizados con laparoscopia están la extracción de cálculos, del apéndice, de la vesícula biliar enferma, la colocación de by-pass gástrico, etcétera [3].
Hace poco más de una década se dio un nuevo avance tecnológico con la aparición de los primeros robots asistentes en operaciones de laparoscopia, de los cuales sus principales exponentes son el robot Zeus [4] y el robot Da Vinci [5]. En este caso el cirujano está cómodamente sentado frente a una consola manipulando dos instrumentos tipo joystick, mientras el paciente en la misma sala o de hecho en cualquier lugar del mundo, está siendo operado con la ayuda de tres brazos robots: uno porta la cámara o endoscopio, y los otros dos siguen fielmente los movimientos del cirujano.
Otro avance muy reciente y con un enfoque diferente en el campo de la cirugía mínimamente invasiva, es la llamada cirugía endoscópica transluminal por orificios naturales (NOTES en inglés) [6-8], que pretende no realizar orificios artificiales como en el caso de la laparoscopia, sino utilizar los orificios naturales con el fin de acceder por medio de ellos a la cavidad abdominal, utilizando para ello la boca, vagina, ano o uretra. Por estos orificios se introduciría tanto el endoscopio flexible como los dos instrumentos que utilizaría el cirujano para realizar la operación. Las ventajas son mayores comparando con la laparoscopia, ya que la incisión o herida se produce al interior del cuerpo humano (por ejemplo en el estómago para después de ahí acceder al órgano en cuestión), con una notable disminución del riesgo de infecciones o complicaciones. En pacientes obesos las ventajas son mucho más claras ya que el tejido adiposo dificulta una intervención laparoscópica. Actualmente diversos equipos médicos empiezan a realizar sus primeras intervenciones de esta técnica, en seres humanos o en animales, que junto con los mini-robots se perfila como una de las tecnologías más prometedoras para el futuro de la cirugía.
El éxito de este nuevo procedimiento se basa ante todo en disponer de un endoscopio e instrumental lo suficientemente flexible y preciso a la vez, que permita llegar a la zona de interés y penetrando por un orificio natural. Es aquí donde la robótica puede proveer de una solución funcional a este problema.
Una posible solución son los robots serpiente ya que su forma y capacidad para navegar por entornos exigentes tales como tuberías, los convierte en una opción viable para el diseño de asistentes robóticos orientados a la cirugía endoscópica transluminal [9-11]. Basados en éstos el presente estudio expone una nueva arquitectura para un asistente robótico transluminal. El documento se estructura de la siguiente manera: la sesión II muestra el modelo matemático del robot, la sesión III presenta el controlador del mecanismo, la sesión IV su funcionamiento en un ambiente en tres dimensiones, y por último la sesión V muestra las conclusiones.
II. MODELADO DEL ROBOT
Los robots serpiente constan de varios cuerpos unidos por articulaciones, permitiendo movimientos que son imposibles para los robots clásicos. Ellos se pueden arrastrar, trepar o nadar, imitando la locomoción de esos reptiles, logrando llegar a sitios vedados a otro tipo de mecanismo autónomo. El aparato digestivo humano, por su anatomía, se convierte en un laboratorio ideal para que esta clase de robots pueda mostrar sus capacidades. Sin embargo, en los avances que hasta ahora se han logrado con la endoscopia transluminal, se han utilizado endoscopios flexibles que requieren del cirujano una gran habilidad.
Construir un endoscopio robótico basado en un robot serpiente daría al cirujano mucha mayor precisión y seguridad en las intervenciones de endoscopia transluminal. Importante es el hecho de que se pueda contar con un instrumento que pueda permanecer rígido y estático respecto a una base, que ofrezca al cirujano una imagen estable y orientable a voluntad, que permita cambiar fácilmente el instrumento instalado en su órgano terminal, y en general, que le provea a él la comodidad de un procedimiento que por el momento es complicado. Incluso en el futuro podría pensarse en la tele cirugía endoscópica transluminal, donde el cirujano trabajaría en una cómoda consola y el robot y paciente estarían ubicados lejos de él y bajo la supervisión de un asistente.
El mecanismo a diseñar estará conformado entonces por varios grados de libertad que a partir de una base situada en la camilla donde se encuentra el paciente y al mismo nivel de la cabeza, le permita sortear la anatomía propia del paciente en la boca, garganta, y esófago, hasta llegar al estómago. En éste último órgano debe disponer de varios grados de libertad con el fin de tener la movilidad suficiente para alcanzar su pared, perforarla y pasar al otro lado, donde deberá tener la suficiente capacidad de movimiento y manipulación. Además, el robot como tal en su órgano terminal constará al menos de tres ramas: una llevará el endoscopio o cámara, y las otras dos llevarán los instrumentos quirúrgicos para realizar la operación.
El hecho de entrar por el aparato digestivo facilita la construcción del robot y la intervención en sí misma, proporcionando un acceso a la cavidad abdominal seguro. Futuros trabajos podrían explorar las otras posibles vías de entrada y sus particularidades mecánicas y médicas.
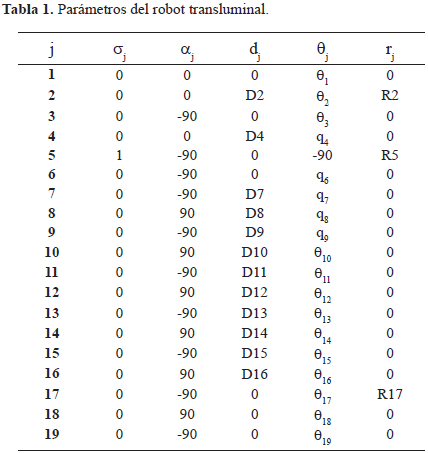
Según las dimensiones normales del cuerpo humano y de la anatomía del aparato digestivo, se diseñó una estructura con diecinueve grados de libertad, conformada por una serie de eslabones que le permiten fácilmente llegar al estómago a través del esófago, teniendo como base fija la camilla sobre la cual se encuentra el paciente. Para este primer diseño solamente se consideró la rama principal del endoscopio. Todas las articulaciones son rotacionales a excepción de la quinta que es prismática y que permite mayor o menor penetración al interior de la cavidad abdominal. La Fig. 1 muestra la arquitectura de este robot, mientras que la Tabla 1 presenta los valores de los parámetros geométricos, según la descripción de Khalil [12]. En esta tabla j designa el número de la articulación, σj se refiere al tipo de articulación (0 para las articulaciones rotacionales, 1 para las prismáticas), αj se refiere al ángulo entre los ejes zj, dj representa la distancia entre los ejes zj, θj simboliza la variable articular rotacional o un ángulo entre los ejes xj, y por último rj simboliza la variable articular prismática o una distancia entre los ejes xj.
A. Modelo geométrico
El modelo geométrico directo (MGD) proporciona la posición y orientación del órgano terminal en función de las posiciones de cada articulación. Para hallarlo es necesario calcular la matriz de transformación homogénea entre cada articulación, según (1) [12-13].
Finalmente todas las diecinueve matrices de transformación se multiplican hasta obtener la matriz 0T19 que proporcionará la posición y orientación del órgano terminal para determinadas posiciones articulares deseadas. Dado el tamaño de esta matriz ella no puede hallarse de forma simbólica sino numérica, utilizando una Matlab Function del programa Matlab®, donde a cada tiempo de muestreo simulado cambia el valor de las articulaciones y por lo tanto de cada matriz de transformación, hallándose finalmente la matriz 0T19 para cada instante de la trayectoria realizada.
De otro lado el modelo geométrico inverso (MGI) entrega todas las posibles posiciones articulares que llevan al órgano terminal a una posición cartesiana deseada. Dada la multitud de soluciones posibles este modelo solamente se puede calcular de manera simbólica para robots de hasta seis grados de libertad. En el caso de este estudio el cálculo se realizó también de manera simbólica, pero haciendo uso de un enfoque original que involucra la matriz Jacobiana del robot. Teniendo en cuenta la relación entre las velocidades articulares (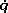 ) y cartesianas (
) y cartesianas (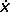 ):
):
Donde J es la matriz Jacobiana del robot, se despeja la velocidad articular para obtener la siguiente expresión:
Esto significa que si se tienen las posiciones cartesianas deseadas (posiciones en tres dimensiones definidas por el usuario, es decir enviadas por un dispositivo tipo joystick), y si se tiene la matriz Jacobiana, es posible hallar las velocidades articulares deseadas y a partir de éstas (integrando) obtener las posiciones articulares necesarias en cada articulación del robot serpiente con el fin de satisfacer la posición deseada por el usuario a través del joystick.
La matriz Jacobiana de un robot puede obtenerse de dos maneras diferentes. La primera consiste en utilizar herramientas de cálculo simbólico para derivar el modelo geométrico directo con respecto al vector de posiciones articulares, opción que no puede utilizarse dada la gran cantidad de articulaciones del robot propuesto. La segunda consiste en utilizar el procedimiento iterativo de cálculo de velocidades que se describe a continuación [12]. Para j desde j = 1 hasta n (número de cuerpos del robot):
Donde jωj y jVj son respectivamente la velocidad angular y linear del origen del sistema de referencia j con respecto al sistema de referencia cero. Ambas velocidades se expresan en el sistema de referencia j. La matriz jAj-1 (3x3) describe la orientación del sistema de referencia j-1 con respecto al sistema j. El vector j-1Pj (3x1) describe la posición del sistema de referencia j en el sistema de referencia j-1. jaj es un vector constante definido por [0 0 1]T. 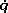 j es la velocidad angular de la articulación j. Como se vio anteriormente σj representa el tipo de articulación. La recurrencia se inicializa con 0ω0 = 0 y 0V0 = 0 dado que la base del robot se supone inmóvil.
j es la velocidad angular de la articulación j. Como se vio anteriormente σj representa el tipo de articulación. La recurrencia se inicializa con 0ω0 = 0 y 0V0 = 0 dado que la base del robot se supone inmóvil.
La ecuación permite calcular las velocidades angular y lineal del sistema de referencia asociado al órgano terminal. Para facilitar la notación se define la función fv de la siguiente manera:
Dada la linealidad de (4) con respecto a las velocidades d e con respecto a las velocidades angulares, la columna i de la matriz Jacobiana puede obtenerse evaluando fv en la posición articular actual y en 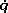 = ei , siendo ei la i-ésima columna de una matriz identidad. El procedimiento del cálculo de la Jacobiana se reduce entonces a aplicar el algoritmo n veces, es decir:
= ei , siendo ei la i-ésima columna de una matriz identidad. El procedimiento del cálculo de la Jacobiana se reduce entonces a aplicar el algoritmo n veces, es decir:
El procedimiento descrito permite el cálculo de la Jacobiana para un vector de posición dado. Todos los cálculos se realizan de manera numérica, lográndose una solución para el modelo geométrico inverso que tiene una precisión de menos de 10x10-17 metros, más que suficiente para este caso.
B. Modelo dinámico
El modelo dinámico inverso (MDI), necesario para la implementación de un controlador basado en el modelo, tal como el control por par calculado [12-13], se halla con base al software Symoro [14], el cual entrega una expresión simbólica del mismo. La expresión general de este modelo es:
Donde Γ son los p ares articulares que van a los motores, A es la matriz de inercia, C la matriz de Coriolis y centrífugas, Q el vector de gravedad, q las posiciones articulares y 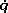 las velocidades articulares.
las velocidades articulares.
Para el caso del modelo dinámico directo (MDD), necesario para simular el sistema en un software como Matlab®, basta con despejar las aceleraciones articulares de (7):
El software Symoro entrega estos dos modelos y a partir de ellos se puede proceder a simular el sistema en el software Matlab®.
III. CONTROL DEL ROBOT
Para realizar el control de este robot se utiliza un control por par calculado, basado en el modelo de la planta que permite el desacoplamiento y la linealización del sistema robot [12-14]. A partir de , si se agrupan la matriz C y el vector Q en la nueva variable H se obtiene:
Asumiendo que las matrices A y H se pueden estimar por medio de 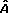 y
y 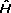 , se realiza la siguiente linealización:
, se realiza la siguiente linealización:
Donde w representa la nueva señal de control. Si el sistema es conocido con cierta precisión, es decir 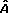
 A y
A y 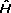
 H, la señal de control w(t) puede ser definida como:
H, la señal de control w(t) puede ser definida como:
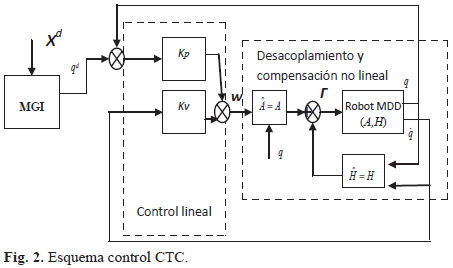
Donde Kp y Kv son las ganancias proporcional y derivativa respectivamente y qd las posiciones articulares deseadas. El esquema de este controlador se muestra en la Fig. 2. Obsérvese que las consignas cartesianas deseadas provenientes del joystick son convertidas a consignas articulares gracias al modelo geométrico inverso (MGI) calculado en línea utilizando la matriz Jacobiana.
IV. RESULTADOS
Con el fin de probar tanto el controlador como todos los modelos involucrados, dos tipos de pruebas se realizaron: a) con una consigna circular de un centímetro de radio (lo cual le exige bastante al controlador y prueba la capacidad del sistema para seguir consignas de reducido tamaño); b) manejo libre del robot siguiendo una trayectoria dada por un dispositivo joystick.
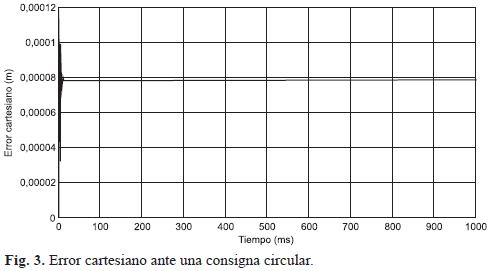
Para el primer caso se obtuvo un error cartesiano bastante pequeño (comparando el círculo deseado con el obtenido), del orden de 1,0x10-4 metros al inicio de la trayectoria (Fig. 3), y aún menor en el transitorio de la señal.
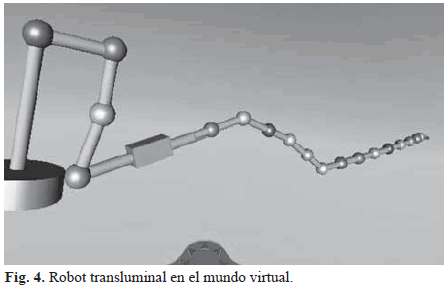
Pero la prueba realmente importante se da para la segunda situación. En este caso se construyó en un ambiente virtual el robot con ayuda del toolbox Simulink 3D Animation de Matlab®, el cual permite implementar pieza por pieza el robot. La Fig. 4 muestra el robot diseñado en la mencionada herramienta, donde puede observarse la curvatura que presenta en lo que sería el paso por la boca, garganta y esófago del paciente, hasta llegar al estómago.
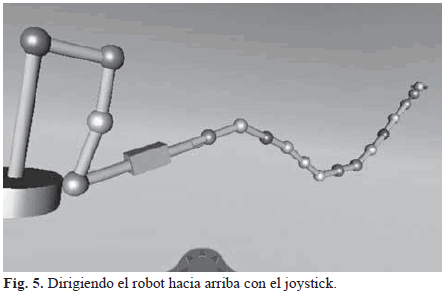
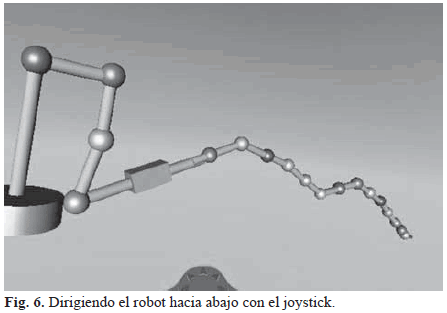
Después se conectó un joystick Genius modelo F-23 al sistema en Simulin® aprovechando que el toolbox antes mencionado permite una entrada directa desde el joystick. La idea es que el robot, en modo flexible, sea introducido por la boca hasta el estómago de manera manual como se hace con los endoscopios tradicionales. Una vez éste llegue al estómago, se pasa a modo controlado donde el robot adopta una posición fija que depende de la anatomía particular del paciente (similar a la mostrada en la Fig. 4). Cuando el órgano terminal del robot se encuentre al interior del estómago el joystick solamente moverá las últimas siete articulaciones, que serán las que se hallarán dentro del órgano, mientras que el resto (las que pasan por la boca, garganta y esófago) se mantienen en una posición fija. Esto evitará que se generen daños involuntarios en las paredes de los órganos no involucrados en la intervención. El paciente por su parte deberá estar sometido a anestesia local o general, a discreción del personal médico. Se pueden además implementar estrategias de control más sofisticadas que tengan en cuenta los movimientos naturales del paciente (respiración o movimientos involuntarios). La Fig. 5 muestra la posición del robot cuando el usuario lo dirige hacia arriba (eje z) con la ayuda del joystick, o hacia abajo (Fig. 6).
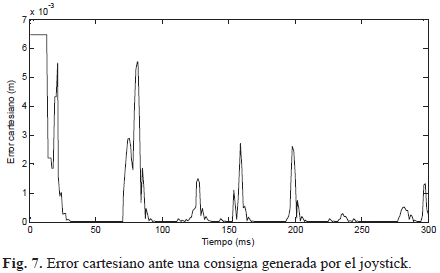
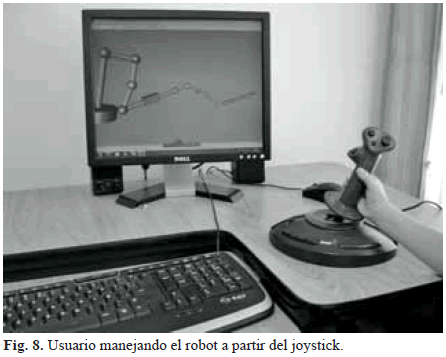
La Fig. 7 muestra el error cartesiano que se presenta en el órgano terminal cuando éste recibe diversas consignas cartesianas a través del joystick. Este error puede llegar a ser de hasta 0,006 m (6 milímetros) cuando el joystick se acciona con rapidez, o de menos de 0,003 m (3 milímetros) cuando el accionamiento es más lento. Es claro que éste último es el adecuado en intervenciones quirúrgicas delicadas como las que se tratan en este estudio. La Fig. 8 presenta una fotografía del usuario controlando el robot a partir del joystick.
V. TRABAJOS FUTUROS
El sistema implementado hasta el momento demostró la viabilidad del nuevo robot para servir como herramienta quirúrgica en cirugía endoscópica transluminal. Hacia el futuro existen aspectos por mejorar o probar como son:
Velocidad de respuesta: La herramienta con la cual se simuló el robot (Matlab/Simulink®) no es la más adecuada en cuanto al manejo en tiempo real. Por esto se llevará próximamente todo el diseño a Visual C++, utilizando las herramientas de manejo gráfico QT y VTK.
Primer prototipo: Un siguiente paso será la construcción de una maqueta que represente la curvatura del aparato digestivo, y sobre ésta introducir un primer prototipo del robot con el fin de probar su movilidad y realizar ajustes tanto de la estructura mecánica como del controlador. Inclusive el robot podría ser movido por una interfaz háptica a fin de probar aspectos tales como la realimentación de fuerza, la interfaz de usuario, o el efecto del robot sobre las paredes del aparato digestivo. El primer prototipo permitirá también evaluar la controlabilidad del dispositivo por parte del cirujano, y si es necesario la implementación de una estrategia de control más sofisticada.
Instrumentos quirúrgicos: No basta solamente con obtener un mecanismo que pueda llegar al estómago a través del aparato digestivo y que porte una cámara de video, sino que pueda llevar en su órgano terminal diversas herramientas que permitan traspasar la pared del estómago y realizar tareas de corte, cauterizado, pinza, o sutura. Esto implica el diseño completo de las tres ramas que compondrán el endoscopio.
Seguridad: Una vez realizadas las consideraciones anteriores se debe hacer un análisis exhaustivo en cuanto a la seguridad del paciente, puesto que se introduce en su interior un dispositivo electrónico. Una opción que se podría manejar es el uso de pocos motores externos los cuales moverían las articulaciones internas por medio de bandas.
VI. CONCLUSIÓN
El presente artículo mostró el diseño de un nuevo robot para cirugía endoscópica transluminal. Este tipo de cirugía mini-invasiva pretende llegar a la cavidad abdominal a través de los orificios naturales del paciente (boca, ano, uretra o vagina). El robot diseñado consta de diecinueve grados de libertad y permitiría llegar al estómago pasando por la boca y el esófago. El robot se introduciría de manera manual aprovechando la flexibilidad que le dan sus numerosos grados de libertad, para después adoptar la forma del aparato digestivo según la anatomía propia del paciente.
Una vez alcanzado el estómago el robot puede ser movido a través de un joystick el cual controla el movimiento de sus últimas articulaciones, las que están precisamente al interior del estómago. Para mover el robot se utiliza un control por par calculado, el cual arroja errores cartesianos del orden de los milímetros cuando el mecanismo es dirigido por el joystick.
Trabajos futuros implementarán el robot en una herramienta que funcione en tiempo real, al mismo tiempo que se construirá un primer prototipo del robot que pueda manejar diferentes instrumentos quirúrgicos.
AGRADECIMIENTO
Los autores agradecen a la Universidad del Cauca el apoyo prestado para el desarrollo de este proyecto, a través de uno de sus proyectos de investigación internos.
REFERENCIAS
[1]. Mühe E. Die Erste Cholecystecktomie Durch das Laparoskop. Langenbecks Arch Klin Chir, 369, 804, 1986. [ Links ]
[2]. Mouret P. How I developed laparoscopic cholecystectomy. Annals of the Academy of Medicine Singapore, 25, 744-747, 1996. [ Links ]
[3]. Jones D.B. Laparoscopic Surgery: Principles and Procedures. Marcel Dekker, 2004. [ Links ]
[4]. Marescaux J., Rubino F. The Zeus robotic system: experimental and clinical applications. Surgical Clinics of North America, 83, 1305-1315, 2003. [ Links ]
[5]. Ballantyne G.H., Molle F. The Da Vinci telerobotic surgical system: the virtual operative field and telepresence surgery. Surgical Clinics of North America, 83, 1293-1304, 2003. [ Links ]
[6]. Kalloo A., Singh V.K., Jagannath S.B. Flexible transgastric peritoneoscopy: a novel approach to diagnostic and therapeutic interventions in the peritoneal cavity. Gastrointestinal Endoscopy, 60, 114-117, 2004. [ Links ]
[7]. Rao G.V., Reddy D.N. Transgastric appendectomy in humans. Proceedings of the World Congress of Gastroenterology, Montréal, Canada, 2006. [ Links ]
[8]. Marescaux, J., Dallemagne B., Perretta S. Surgery without scars: report of transluminal cholecystectomy in a human being. Archives of Surgery, 142, 823-826, 2007. [ Links ]
[9]. Lipkin K., Brown I., Peck A., Choset H., Rembisz J., Gianfortoni P., Naaktgeboren A. Differentiable and Piecewise Differentiable Gaits for Snake Robots. Proceedings of the International Conference on Intelligent Robots and Systems, San Diego, USA, 2007. [ Links ]
[10]. Johnson A., Wright C., Tesch M., Lipkin K., Choset H. A novel architecture for modular snake robots. Technical report, Robotics Institute, Carnegie Mellon University, USA, 2011. [ Links ]
[11]. Hopkins J.K., Spranklin B.W., Gupta S.K. A survey of snakeinspired robot designs. Bionispiration and Biomimetics, 4, 2009. [ Links ]
[12]. Khalil W., Dombre E. Modeling, Identification and Control of Robots. Kogan Page Science, 2002. [ Links ]
[13]. Vivas A. Diseño y Control de Robots Industriales: Teoría y Práctica. Elaleph, 2010. [ Links ]
[14]. Sciavicco L., Siciliano B. Modeling and Control of Robot Manipulators. McGraw-Hill, 1996. [ Links ]