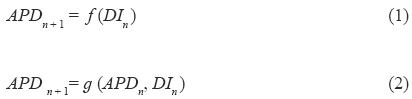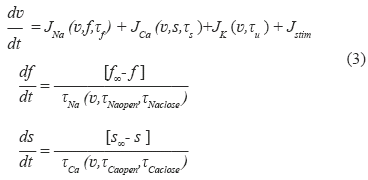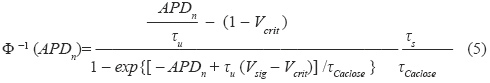Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares en
SciELO
Similares en
SciELO -
 Similares en Google
Similares en Google
Compartir
Revista Ingeniería Biomédica
versión impresa ISSN 1909-9762
Rev. ing. biomed. vol.7 no.13 Medellín ene./jun. 2013
MODELO PARAMÉTRICO DE LA ACTIVIDAD ELÉCTRICA CELULAR CARDIACA ESTIMADO A PARTIR DE REGISTROS ELECTROCARDIOGRÁFICOS ESTÁNDARES
PARAMETRICAL MODEL OF CARDIAC CELL ELECTRICAL ACTIVITY ESTIMATED FROM STANDARD ELECTROCARDIOGRAM RECORDINGS
Alfredo Illanes1,2, Guillaume Sérandour1
1 Facultad de Ciencias de la Ingeniería, Universidad Austral de Chile, Valdivia, Chile.
2 Dirección para correspondencia: alfredoillanes@uach.cl.
Recibido 1 de febrero de 2013. Aprobado 10 de abril de 2013
RESUMEN
El presente trabajo tiene como objetivo principal relacionar la actividad eléctrica cardiaca celular con la actividad eléctrica cardiaca medida en una sola derivación del electrocardiograma (ECG), mediante un modelo paramétrico de potencial de acción (PA) celular, lo cual se llevó a cabo relacionando dinámicas conocidas, matemáticamente modelables, que existen a nivel de una célula cardiaca, a dinámicas que pueden ser encontradas en un registro ECG estándar. La principal dinámica celular a relacionar con el ECG es la conocida como curva de restitución celular en tres dimensiones, la cual relaciona la duración del potencial de acción celular (APD) con el intervalo diastólico que lo precede y con el mismo APD pero del ciclo cardiaco precedente. Curvas de restitución similares se encontraron en señales ECG registradas durante el test isométrico handgrip, relacionando el intervalo QT con el intervalo TQ que lo precede y con el intervalo QT del ciclo cardiaco precedente. Siguiendo esta similitud, un modelo paramétrico de curva de restitución, extraído de un modelo de PA a tres corrientes iónicas, es ajustado a la curva de restitución del ECG con el fin de estimar los parámetros del modelo de PA. Este modelo es finalmente simulado estimulándolo con un tren de impulsos de frecuencia igual a la frecuencia cardiaca del sujeto experimentado. Los resultados muestran que la curva de restitución obtenida experimentalmente a partir del ECG es similar a la obtenida a partir de la simulación del modelo de PA. Más aún, el APD simulado del modelo sigue de forma satisfactoria la variación en el tiempo del intervalo QT del sujeto experimentado. Esto abre nuevas perspectivas en el análisis de la actividad celular a partir de registros ECG estándar.
PALABRAS CLAVE: Modelado ECG, modelo de potencial de acción celular, intervalo QT, APD, curva de restitución.
ABSTRACT
The main purpose of this paper is to relate cellular cardiac electrical activity with the cardiac electrical activity measured in only one electrocardiogram (ECG) lead, through a cellular action potential (AP) parametrical model. This is performed by relating known dynamics, which can be mathematically modeled, existing at a cardiac cell level, to dynamics which can be obtained from a standard ECG recording. The main cellular dynamic used for relating with the ECG is the one known as three dimensional cellular restitution curve, which relates the action potential duration (APD) with its preceding diastolic interval and with the APD of the preceding cardiac cycle. Similar restitution curves were found in ECG signals recorded under the isometric handgrip test by relating the QT interval with its preceding TQ interval and with the QT interval of the preceding cardiac cycle. Following this similarity, a parametrical restitution curve, derived from a three ionic current cellular AP model was fitted to the ECG restitution relation for AP model parameter estimation. This model is finally simulated by stimulating it with an impulse train of frequency similar to the heart rate of the tested subject. The results show that the restitution curve experimentally obtained from the ECG is similar to the one obtained from de AP model simulation. Moreover the simulated APD follows satisfactorily the QT interval time variation of the tested subject. This opens new perspectives for the analysis of cellular cardiac electrical activity from standard ECG recordings.
KEY WORDS: ECG modelling, cellular action potential model, QT interval, APD, restitution curve.
I. INTRODUCCIÓN
El electrocardiograma (ECG) posee un gran valor clínico para el diagnóstico de trastornos del ritmo y de la conducción eléctrica cardiacos. Éste describe la actividad eléctrica del corazón captada por electrodos (al menos dos) localizados en la superficie del cuerpo. Cada ciclo cardiaco se caracteriza en el ECG por una sucesión de eventos conocidos como la onda P, el complejo QRS y la onda T. Los intervalos de tiempo entre inicios y términos de estos distintos eventos son importantes para el diagnóstico, pues reflejan procesos electrofisiológicos que ocurren al interior del corazón y que por ende entregan información significativa acerca de la actividad eléctrica cardiaca.
Aunque el ECG corresponde a un procedimiento no-invasivo de adquisición de datos que permite acceder a la dinámica global de la actividad eléctrica del corazón, la información obtenida de esta manera es difícil de analizar. En efecto, esta información es el resultado de una suma de actividades microscópicas localizadas al interior del cuerpo y transmitidas a través de un medio no homogéneo [1,2]; entre los electrodos y el corazón se encuentran una diversidad de órganos y tejidos. Es decir que las señales captadas en un registro electrocardiográfico corresponden a una medida de la actividad eléctrica cardiaca a escala macroscópica que encuentra su origen a escala microscópica, a nivel de potenciales celulares. Esto hace que sea un problema complejo la extracción de información de la actividad eléctrica cardiaca celular a partir de técnicas no invasivas como el ECG.
Diversos trabajos han tenido como objetivo el estudio de esta compleja relación entre la actividad eléctrica celular cardiaca y sus proyecciones en potenciales de superficie del cuerpo a nivel ECG. En una primera categoría se encuentran trabajos que relacionan experimentalmente intervalos del ECG con intervalos medibles a nivel de potenciales de acción celular. En [3] y [4] se estudiaron los efectos de la frecuencia cardiaca sobre el intervalo QT del ECG. Ambos trabajos muestran similitudes entre estos efectos y los producidos por la frecuencia de excitación del tejido cardiaco sobre la duración del potencial de acción celular. En los trabajos presentados en [5,6] se realizaron estudios experimentales acerca de la dependencia del intervalo QT con el intervalo TQ del ECG y se encontraron relaciones similares con la dependencia existente a nivel celular entre el intervalo diastólico y la duración del potencial de acción.
Si bien los trabajos citados anteriormente ponen en evidencia relaciones entre intervalos a nivel ECG e intervalos a nivel celular, estos sólo exploran el ámbito experimental y no relacionan analíticamente ambos niveles por medio de modelos matemáticos. En este sentido cabe mencionar el trabajo presentado en [7] donde un modelo a dos variables de estado del potencial de acción celular fue ajustado a señales ECG por medio de una relación de restitución a dos dimensiones.
Un área de investigación que aborda el estudio de la relación entre potenciales medidos a nivel de superficie del cuerpo a potenciales celulares por medio de modelos matemáticos es el que concierne al problema inverso del ECG. Este consiste en la caracterización de un modelo matemático de la actividad eléctrica celular cardiaca a partir de señales ECG [8-13]. En general el problema directo (la generación de señales ECG a partir de un modelo de actividad eléctrica celular cardiaca) se resuelve calculando una función de transferencia que relaciona los potenciales medidos a nivel de la superficie del cuerpo con las fuentes localizadas al interior del corazón [8,10]. Con el fin de resolver el problema inverso es necesario invertir esta función de transferencia. Este proceso de inversión es generalmente complejo debido a que hay menos información en las señales ECG que la requerida para la caracterización del modelo. Con el fin de superar este problema es necesario utilizar un gran número de electrodos en la superficie del cuerpo con el fin de obtener una mayor cantidad de observaciones (señales ECG) [8]. La desventaja de esta solución es que se transforma en un procedimiento que no es estándar, por lo cual no se puede llevar a cabo con electrocardiógrafos convencionales.
El objetivo de este trabajo es relacionar la actividad eléctrica cardiaca celular con la actividad eléctrica cardiaca medida en una sola derivación del electrocardiograma (ECG), mediante un modelo paramétrico de potencial de acción (PA) celular, lo cual se llevó a cabo relacionando dinámicas conocidas, matemáticamente modelables, que existen a nivel de una célula cardiaca, a dinámicas que pueden ser encontradas a nivel de un registro ECG estándar. El punto clave de este enfoque es la relación entre intervalos de tiempo medibles en señales ECG e intervalos definidos a nivel celular, mediante un modelo paramétrico de potencial de acción (PA) celular cuyos parámetros pueden ser estimados a partir de un registro ECG.
La principal dinámica celular que se quiere explotar para relacionar ambas escalas es la relación existente entre la duración del potencial de acción celular (APD) y el intervalo diastólico (DI), ambos parámetros utilizados para describir la actividad eléctrica y de reposo de una célula respectivamente. En efecto, se ha logrado demostrar en investigaciones tanto experimentales [14-18] como analíticas [19-21] que el tejido cardiaco posee una memoria que se ve reflejada en una relación entre el APD y el DI, tanto de ciclos presentes como de ciclos pasados. De hecho, la relación entre un APD y su DI que lo precede directamente tiene una forma de onda bien definida conocida como curva de restitución celular [18, 20-22]. Esta relación de restitución ha sido largamente estudiada y permite evaluar ciertas características del comportamiento cardiaco, particularmente el riesgo de alternancias [21, 23-27], un ritmo cardíaco anormal, caracterizado por variaciones en la duración del APD entre dos ciclos cardiacos y que podría estar detrás de la activación de arritmias cardiacas de gravedad.
Se han encontrado igualmente relaciones de restitución celulares en tres dimensiones, relacionando el APD actual no solo a su DI precedente sino que también a su APD precedente. Estas relaciones se han presentado tanto en trabajos experimentales [28, 29], como en trabajos analíticos [19, 30].
Los resultados obtenidos muestran que el APD simulado del modelo sigue de forma satisfactoria la variación en el tiempo del intervalo QT del sujeto testeado, lo cual abre nuevas perspectivas en el análisis de la actividad celular a partir de registros ECG estándar.
Cabe señalar que algunos resultados preliminares de este trabajo fueron presentados en [31].
1.1. La curva de restitución celular
El propósito de esta sección es introducir algunos conceptos para una mejor comprensión del objetivo del presente trabajo y sobre todo para entender los parámetros que involucra la relación de restitución a nivel celular.
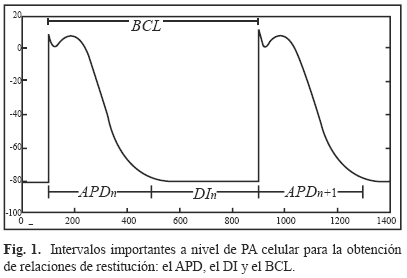
Cuando un estímulo eléctrico de amplitud suficiente llega a una célula excitable, el potencial al interior de la célula se vuelve rápidamente positivo con respecto al exterior de ésta. Este proceso es conocido como despolarización celular. El proceso inverso, cuando la célula cardiaca estimulada vuelve a su estado de reposo, se conoce como repolarización celular. El registro de las diferencias de potencial medidas entre los medios intracelulares y extracelulares durante los procesos de despolarización-repolarización de una célula cardiaca corresponde al potencial de acción celular (llamado AP por la abreviación en inglés de Action Potential). La duración de ambos procesos es conocido como la duración del potencial de acción (llamado APD por la abreviación en inglés de Action Potential Duration) y el intervalo de tiempo entre el fin de la repolarización celular y la llegada del próximo estímulo eléctrico es conocido como el intervalo diastólico (llamado DI por la abreviación en inglés de Diastolic Interval). El APD y el DI están relacionados por medio del periodo de excitación celular (llamado BCL por la abreviación en inglés de Basic Cycle Length) que corresponde al intervalo de tiempo entre dos excitaciones sucesivas. Estos tres intervalos (APD, DI, BCL), que se pueden observar en la Fig. 1, son importantes para la comprensión del concepto de relación de restitución celular.
Cuando el corazón late a una cierta frecuencia, el APD debe ajustarse con el fin de asegurar un bombeo efectivo de sangre. Un incremento de la frecuencia cardiaca requiere una disminución del APD y del DI, lo que resulta en sístoles y diástoles eléctricas más cortas. Para una concordancia correcta entre las fases de llenado y eyección de los ventrículos, las variaciones del APD y del DI están fuertemente relacionadas. La dinámica de este proceso se conoce como restitución eléctrica. El comportamiento dinámico de esta relación ha sido estudiado en diversos trabajos [14-18, 26, 32].
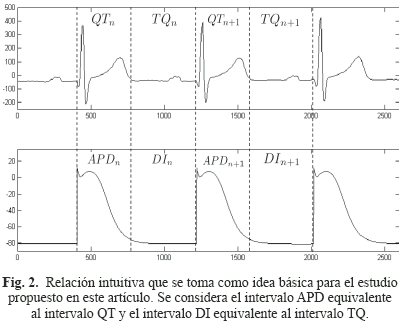
Esta relación de restitución puede ser descrita matemáticamente tanto para una relación de restitución a dos variables, entre el APD actual y su DI precedente (1), como para una relación de restitución a tres variables, entre el APD actual, el DI que lo precede y el APD del ciclo precedente (2):
donde los subíndices n y n + 1 denotan el número de ciclo cardiaco. La curva que representa esta relación, tanto en dos como en tres dimensiones, es la llamada curva de restitución celular. Las funciones f y g de (1) y (2) son generalmente determinadas de forma experimental. En la literatura la mayoría de los modelos empíricos de la curva de restitución tienen una forma exponencial [22, 33].
Diversos protocolos de excitación celular han sido utilizados con el objetivo de registrar la curva de restitución celular. Los más utilizados son los conocidos como protocolo S1-S2 y protocolo dinámico. El primero consiste en enviar una secuencia de impulsos a un BCL constante para enseguida enviar un estímulo prematuro individual [15]. El segundo consiste primeramente en excitar la célula a un BCL constante y enseguida, cuando todos los transitorios se hayan desvanecido, progresivamente disminuir el BCL [17].
La importancia de la curva de restitución en la caracterización de dinámicas cardiacas ha sido enfatizada en numerosos estudios [29, 30]. Es conocido que la restitución del APD es de importancia fundamental en dinámicas cardiacas. En particular, la pendiente de la curva de restitución está relacionada a la ocurrencia de alternancias [21, 22, 33, 34], un ritmo cardiaco anormal que se caracteriza por dinámicas de larga y corta duración del APD y que pueden estar detrás de ciertas patologías cardiacas [23, 24, 27].
II. MATERIALES Y MÉTODOS
En esta sección se detalla la metodología y el procedimiento de adquisición de datos para estimar los parámetros de un modelo de potencial de acción (PA) a partir de una sola derivación del ECG. Esta metodología y los registros utilizados son los mismos que en el trabajo presentado en [7] pero ahora con el objetivo de obtener curvas de restitución basadas en el ECG que poseen tres dimensiones (ECG-RC3D), las cuales servirán para estimar los parámetros de un modelo a tres corrientes iónicas (en [7] se trabajó con un modelo a dos corrientes iónicas).
Como se explicó en las secciones anteriores el principal comportamiento dinámico de la actividad eléctrica celular considerada en este trabajo está caracterizado por la curva de restitución que relaciona los APDs y DIs de distintos ciclos cardiacos. Con el fin de relacionar actividades cardiacas observadas a nivel celular y a nivel ECG, los intervalos QT y TQ son utilizados para obtener relaciones de restitución a nivel ECG.
La analogía entre intervalos a nivel celular y ECG sobre la cual se basa este trabajo se ilustra en la Fig. 2. Desde un punto de vista fisiológico, la representación mostrada por esta figura es incorrecta, sin embargo explica intuitivamente la idea básica detrás de este estudio. Esta idea se apoya en el hecho de que el intervalo QT está relacionado con los APDs de un gran número de células, los cuales varían de sitio en sitio en los ventrículos [34, 35].
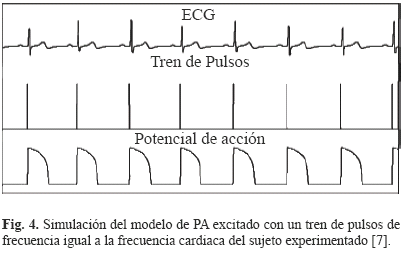
La Fig. 3 resume las etapas para estimar los parámetros del modelo de PA a tres corrientes iónicas a partir de un registro ECG de una derivación. Estas etapas serán presentadas en detalle en las próximas secciones. La señal ECG resultante del test handgrip entra primeramente a una etapa de segmentación, a partir de la cual se calculan los intervalos QT y TQ para cada ciclo cardiaco. Luego se obtiene la ECG-RC3D graficando, en la fase de contracción durante el test del handgrip, el intervalo QT del ciclo cardiaco n + 1 (QTn + 1) en función de los intervalos TQ y QT en el ciclo cardiaco anterior (TQn y QTn). A esta curva obtenida experimentalmente a nivel ECG se le ajusta una curva de restitución paramétrica extraída del modelo de PA, obteniendo cuatro parámetros del modelo de PA. El resto de los parámetros del modelo de PA se estiman por medio de la simulación de este mismo, utilizando como entrada un tren de pulsos cuya frecuencia está dada por la frecuencia cardiaca del ECG del sujeto experimentado (ver Fig. 4). Finalmente, a partir del PA simulado, se miden el APD y el DI para cada ciclo cardiaco y se comparan las curvas de restitución celular obtenidas del modelo con las ECG-RC3D obtenidas experimentalmente. Igualmente se comparan la variación del intervalo QT obtenido experimentalmente a partir del ECG con la del intervalo APD simulado del modelo.
2.1. El ejercicio isométrico handgrip
A nivel ECG, tal como a nivel celular (ver Sección 1.1), es necesario un protocolo de registro que permita generar dinámicas de aceleración y deceleración de la frecuencia cardiaca para obtener variaciones importantes de los intervalos QT y TQ. Esto se logra con el test isométrico handgrip al cual es sometido el sujeto examinado.
Este examen consiste en que el sujeto realice una contracción isométrica voluntaria con su mano contra una resistencia ajustable por medio de resortes. Un ejercicio isométrico es un tipo de ejercicio durante el cual los músculos no sufren cambio de longitud pero generan una tensión mucho mayor que lo que se observa en estado de reposo. Este ejercicio produce dos efectos esenciales para este estudio:
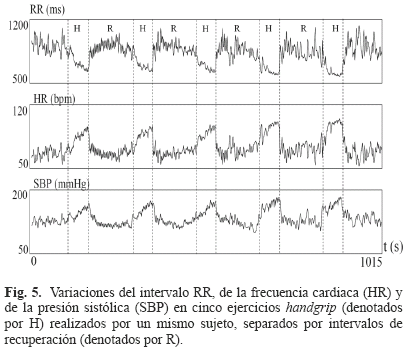
- Conduce a un rápido incremento de la frecuencia cardiaca al inicio del esfuerzo (ver Fig. 5).
- Asegura una variación importante de los intervalos QT y TQ del ECG. Posee igualmente dos ventajas prácticas importantes:
- Es un ejercicio de fácil implementación.
- Provee una señal ECG de buena calidad ya que posee muy bajo ruido de electromiograma debido a la poca actividad muscular que el ejercicio requiere.
El test handgrip es de alguna forma similar al que se realiza a nivel celular con el protocolo de estimulación presentado en [16], donde se producen aceleraciones y deceleraciones abruptas sostenidas de la frecuencia de excitación (en el caso del ECG de la frecuencia cardiaca). El test handgrip es un ejercicio que desencadena casi instantáneamente una respuesta cardiaca parasimpática lo que resulta en rápidos incrementos de la frecuencia cardiaca y la presión arterial [36] como se puede observar en la Fig. 5.
2.2. Procedimiento de adquisición de datos
Los registros utilizados en el presente trabajo corresponden a los mismos registros utilizados en [7]. A continuación se presentará en detalle el procedimiento con el cual se adquirieron dichos registros.
Se realizaron registros ECG de una derivación (DII) en 16 sujetos voluntarios adultos sanos a una frecuencia de muestreo de 500 Hz, utilizando un dispositivo A/D (PowerLab, ADInstrumentation, Australia). Los datos fueron procesados utilizando los software científicos Matlab [37] y Scilab [38].
Para el experimento cada sujeto se sienta relajadamente en un sillón y la mano que sostiene el dispositivo handgrip permanece en una superficie plana. Como entrenamiento el sujeto realiza con el dispositivo handgrip unas pocas contracciones voluntarias de 5 segundos de duración cada una, separadas de fases de un minuto de recuperación entre las dos contracciones. Este primer paso permite asegurar que el esfuerzo requerido corresponde a un esfuerzo entre 20% y 30% de una contracción voluntaria máxima. Una intensidad de esfuerzo inferior podría no producir los efectos handgrip deseados y en el caso de intensidades de esfuerzo muy altas sería muy difícil mantener este esfuerzo durante 60 segundos.
Luego de la etapa de entrenamiento y de una etapa de reposo de 10 minutos, el sujeto es sometido a cuatro ejercicios Handgrip de 60 segundos, separados de intervalos de recuperación de dos minutos.
2.3. Obtención de la curva de restitución en tres dimensiones a partir del ECG
Con el fin de obtener una curva de restitución a nivel ECG se requieren los siguientes pasos:
- Registro del ECG durante el test handgrip.
- Cálculo automático de los intervalos QT y TQ del ECG.
El primer paso ya fue explicado en la sección anterior por lo que esta sección se dedicará a presentar en detalle el cálculo del intervalo QT.
La Fig. 6 muestra un diagrama de bloques que presenta los pasos para segmentar automáticamente el ECG con el fin de calcular los instantes de principio de complejo QRS y fin de la onda T. Estos instantes son utilizados para el cálculo de los intervalos QT y TQ. En una primera etapa la señal ECG es filtrada utilizando un filtro pasabanda con frecuencias de corte [0.05 100] Hz con el fin de atenuar ruidos de la deriva de línea de base y ruidos de alta frecuencia. El filtro consiste en aplicar la Transformada Rápida de Fourier (FFT) a la señal ECG para luego truncar las componentes frecuenciales indeseables y finalmente aplicar la FFT inversa.
En una segunda etapa se detecta automáticamente el umbral de la onda R del ECG. Este instante sirve como referencia para la búsqueda posterior de los instantes de principio de complejo QRS y fin de la onda T. Para la detección del umbral de la onda R se utilizó el algoritmo presentado en [39, 40]. Este algoritmo consiste principalmente en el cálculo de un indicador basado en la amplitud y la curvatura de la señal ECG. Es bien sabido que en general la onda R posee la amplitud y curvatura más grande en una señal ECG, por lo cual este indicador diferencia de manera bastante eficaz la onda R del resto de las ondas del ECG.
Luego de una etapa de ventaneado que sirve a delimitar groseramente cada uno de los instantes a detectar, se procede a detectar el principio del complejo QRS y el fin de la onda T. La detección del principio del complejo QRS se realizó utilizando el algoritmo presentado en [39]. Este algoritmo consiste en el cálculo de la envolvente del ECG con el fin de desmodular el complejo QRS en una señal tipo campana de Gauss, cuyo principio y fin coincide con el principio y fin del complejo QRS.
La detección del fin de la onda T es conocida por ser una tarea bastante compleja, especialmente en señales ECG no estacionarias. El algoritmo propuesto en [41] ha sido elegido para ser utilizado en este estudio debido a su robustez frente al ruido y a las no estacionaridades del ECG. Este algoritmo está basado en el cálculo de un área que está parcialmente delimitada por la onda T. La consistencia de este algoritmo ha sido probada asumiendo esencialmente la hipótesis de concavidad de la onda T. La confiabilidad que presenta este algoritmo es esencial para el objetivo de este estudio.
Finalmente la ECG-RC3D se obtiene de la misma forma que en [7], pero esta vez agregando un eje más, esto es, graficando el intervalo QT al ciclo cardiaco n+1 en función de los intervalos TQ y QT al ciclo cardiaco n.
2.4. Modelo de Potencial de acción celular y relación de restitución analítica
Lo que se busca en este estudio es poner en relación dinámicas ECG con dinámicas celulares por medio de un modelo de PA celular. Claramente el modelo debe ser simple y de baja cantidad de parámetros para que éstos puedan ser estimados a partir de una sola derivación del ECG. Por ende la relación se debe focalizar en dinámicas específicas que ocurren a nivel de una célula. Como se presentó en la Sección 1.1, la principal dinámica celular a relacionar en el ECG es la dinámica de restitución celular, por lo cual el modelo de PA utilizado debe ser capaz de reproducir dicha dinámica.
En [7] se utilizó el modelo de PA presentado en [20] para relacionar nivel celular con nivel ECG en registros realizados durante el test handgrip. Este modelo permitió extraer una curva de restitución celular analítica de dos dimensiones, como la de la ecuación (1), la cual permite ajustar una curva de restitución dos dimensiones, obtenida a partir del ECG.
En el presente trabajo se realizó un estudio similar al realizado en [7] con la diferencia que se utilizan relaciones de restitución de tres dimensiones como la de la ecuación (2). Para ello se utilizó un modelo de PA celular del cual es posible extraer una curva de restitución analítica en tres dimensiones. El modelo de PA utilizado en este trabajo es el modelo presentado en [19], descrito por el sistema de ecuaciones (3):
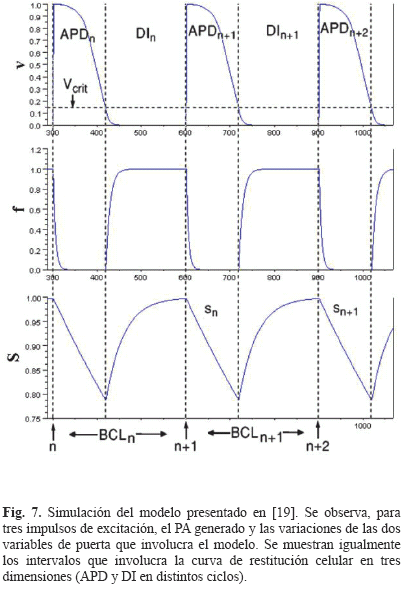
Este modelo corresponde a un modelo de PA celular a tres corrientes iónicas, las cuales corresponden indirectamente a las corrientes iónicas de sodio JNa, de calcio JCa y de potasio JK respectivamente. El modelo posee tres variables de estado, una correspondiente al potencial de acción v, y las otras dos correspondientes a variables de puerta que regulan las entradas de iones sodio (f) y calcio (s). Una simulación de estas tres variables de estado que involucra el modelo se puede observar en la Fig. 7.
La corriente iónica de sodio corresponde a una corriente de dinámica rápida dependiente del potencial v, de la variable de puerta f y de una constante de tiempo τf que representa la dinámica del sodio entrante en la célula. La corriente iónica de calcio corresponde a una corriente de dinámica lenta dependiente igualmente de v, de la variable de puerta s y de una constante de tiempo τs que representa la dinámica de iones calcio entrando en la célula. La corriente iónica de potasio no está regulada por una variable de puerta, solo depende de v y de su constante de tiempo τu que representa la dinámica de iones potasio saliendo de la célula. Las variaciones de las variables de puerta f y s dependen de constantes de tiempo con las cuales se abren y cierran las compuertas que dejan entrar las corrientes de sodio (τNaopen y τNaclose) y calcio (τCaopen y τCaclose) respectivamente. La corriente de estimulación Jstim corresponde a una corriente externa que consiste en un tren de pulsos de alrededor de 1 ms de duración. Para mayores detalles acerca del modelo se sugiere consultar el trabajo presentado en [19]. En total el modelo involucra siete parámetros correspondientes todos a las constantes de tiempo que rigen las entradas y salidas de iones de la célula.
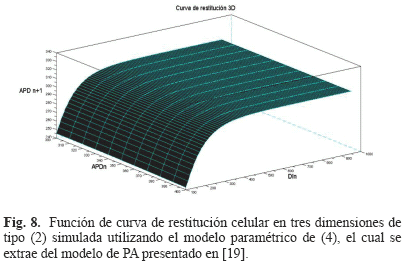
Una de las ventajas de este modelo es que a partir de éste es posible extraer una fórmula paramétrica explícita para una curva de restitución celular en tres dimensiones. Esta ventaja es fundamental para la estimación de la mayoría de los parámetros del modelo de PA celular a partir del ECG. Esta fórmula es de la forma dada en la ecuación (2), donde la función g consiste en una función tipo exponencial en tres dimensiones (ver Fig. 8) cuyo modelo paramétrico se muestra en (4). Se sugiere consultar [19] para mayores detalles acerca de la extracción de (4) a partir de (3).
donde,
Vcrit y Vsig corresponden simplemente a umbrales de voltaje a la cual la célula responde por un potencial de acción.
De acuerdo a lo anterior el modelo de PA de (3) involucra siete parámetros, por lo cual el vector de parámetros a estimar en el modelo de PA es:
θPA=[τf ,τs,τu,τNaopen,τNaclose,τCaopen,τCaclose]
Mientras que el modelo analítico de curva de restitución celular de (4) involucra cuatro parámetros. Por lo cual el vector de parámetros que es posible estimar a partir del modelo de curva de restitución celular es:
θCR=[τs,τu,τCaopen,τCaclose]
Este vector de parámetros es estimado ajustando el modelo paramétrico de curva de restitución celular de (4) a la curva de restitución experimental obtenida a partir del ECG, (ECG-RC3D) utilizando el método de mínimos cuadrados no lineal.
Finalmente los tres parámetros restantes de (3), esto es, [τf ,τNaopen ,τNaclose] son estimados minimizando el error cuadrático promedio entre el APD simulado del modelo de PA y el intervalo QT obtenido experimentalmente del ECG (para mayores detalles ver [7]).
III. RESULTADOS
En esta sección se presentan los principales resultados obtenidos en este trabajo. Estos pueden ser divididos en cuatro partes: variación de los intervalos TQ y QT durante el test del handgrip, obtención de la ECG-RC3D experimentales, ajuste de esta curva basada en el ECG por medio de la curva de restitución analítica de (4), y simulación del modelo de PA a tres corrientes iónicas utilizando los parámetros estimados a partir del ECG. En esta última parte se presentarán las curvas de restitución simuladas y experimentales así como también las variaciones de los intervalos APD a nivel celular y QT a nivel ECG.
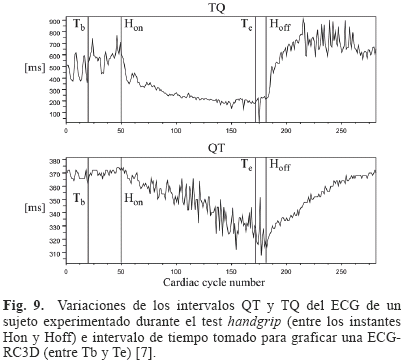
Para poder obtener la ECG-RC3D, tal como a nivel celular, es necesario registrar el ECG bajo un protocolo que permita una variación suficiente de los intervalos involucrados en la relación de restitución. Estas variaciones se logran mediante el test del handgrip, cuya utilización permitió obtener curvas de restitución en dos dimensiones en [7]. La Fig. 9 muestra las variaciones del intervalo QT y TQ del ECG durante una contracción voluntaria realizada en el test handgrip [7]. Se observa que al ciclo cardiaco correspondiente al inicio del esfuerzo (Hon), tanto el intervalo TQ como el intervalo QT comienzan a disminuir, pero sin la misma dinámica. Por un lado el intervalo TQ presenta una disminución rápida al comienzo del esfuerzo para luego estabilizarse lentamente en un valor casi estacionario. La recuperación de este intervalo es rápida luego de que se pone fin a la contracción (Hoff). Por otro lado el intervalo QT disminuye linealmente durante el proceso de contracción sin alcanzar un valor estacionario, para luego, al término de la contracción, recuperarse linealmente con una pendiente muy similar a la producida por la fase de contracción. Estas dinámicas muestran de qué forma tanto el intervalo QT como el TQ se van ajustando a los requerimientos generados durante el primer minuto del test handgrip, de una manera similar a lo que sucede a nivel celular con el APD y el DI.
La Fig. 10 muestra las ECG-RC3D obtenidas durante la fase de contracción en el test handgrip para cuatro sujetos diferentes. Se puede observar claramente la forma exponencial en tres dimensiones que rige la relación entre los intervalos QTn + 1, TQn y QTn durante el test handgrip. Esta relación es similar a la encontrada a nivel celular entre el APDn + 1, DIn y APDn [28-30]. A estas curvas de restitución se les ajustó el modelo analítico de curva de restitución celular de (4) con el fin de estimar las cuatro contantes de tiempo de este modelo como se puede observar en la Fig. 11.
Las figuras 12 y 13 comparan los resultados de las simulaciones del modelo de PA con los parámetros estimados a partir del ECG. La Fig. 12 muestra una comparación entre la ECG-RC3D (círculos negros) y la curva de restitución resultante de la simulación del modelo de PA (círculos rojos) con todos los parámetros estimados. Se puede observar que tanto la ECG-RC3D experimental como la curva de restitución simulada tienen forma exponencial y sus puntos se distribuyen en el espacio de tres dimensiones en coordenadas similares. Más aún, si se compara la variación del intervalo QT obtenida experimentalmente a partir del ECG registrado durante el handgrip y la variación del APD simulado del modelo de PA (ver Fig. 13) se puede ver que ésta última sigue de manera satisfactoria el QT experimental. Esto quiere decir que, desde un punto de vista de dinámicas de restitución en tres dimensiones, el modelo paramétrico de PA es identificable a partir de las observaciones correspondientes al ECG través del modelo de curva de restitución.
IV. DISCUSIÓN Y CONCLUSIÓN
En este trabajo se presentó un estudio que tenía como finalidad relacionar dinámicas eléctricas cardiacas que ocurren a dos niveles diferentes. Por un lado la actividad eléctrica celular cardiaca a un nivel microscópico y por otro lado los potenciales registrados a nivel macroscópico en la superficie del cuerpo con el ECG. La idea principal fue utilizar una dinámica específica que ocurre a nivel celular, que permitiera ser modelada en función de un modelo paramétrico simple, con el fin de poder relacionarlas a solo una derivación del ECG. Esto se hizo por medio de la identificación de un modelo paramétrico de PA celular cuyos parámetros pudieran ser estimados a partir de una señal ECG.
Los resultados experimentales obtenidos demostraron que la ECG-RC3D que relaciona los intervalos QT y TQ en una sola derivación del ECG es similar a la extensamente estudiada curva de restitución celular que relaciona el APD con el DI de distintos potenciales de acción. Esto permitió relacionar dinámicas ECG a dinámicas celulares por medio de un modelo de potencial de acción celular a tres corrientes iónicas que pudo ser completamente identificado gracias la similitud de dinámicas de restitución que ocurren a nivel celular y a nivel ECG. Prueba de esta identificación es que los parámetros estimados del modelo de PA a partir del ECG permitieron simular este modelo resultando en similitudes satisfactorias entre las dinámicas obtenidas experimentalmente con un sujeto dado y dinámicas generadas de un modelo matemático cuyos parámetros son propios del sujeto experimentado.
Si bien es cierto los registros ECG utilizados en este trabajo son exactamente los mismos que los utilizados en [7], donde se obtuvieron curvas de restitución en dos dimensiones, el estudio se focalizó en relaciones de restituciones en tres dimensiones con el fin de identificar un modelo de PA de mayor complejidad que en [7]. Esto nos permite identificar el proceso en base a un modelo que posee más grados de libertad que en [7] y por ende un mayor nivel de detalle en las dinámicas eléctricas celulares. Más aún, el nuevo modelo utilizado [19] involucra variables que poseen una significancia fisiológica mayor que el modelo utilizado en [7], ya que involucra tres corrientes iónicas correspondientes al Na+, Ca+ y K+ (el modelo presentado en [20] y utilizado en [7] involucra únicamente corrientes equivalentes de entrada y salida).
Con esto se abren diversas perspectivas que podrían ser importantes en electrocardiografía en un futuro cercano, sobre todo considerando que se utilizan registros ECG estándar. Una primera posible aplicación es adaptar los estudios ya hechos a nivel de curva de restitución celular a la curva de restitución basada en el ECG. Como se vio en la Sección 1.1, estudios realizados a nivel celular han mostrado que la forma de la curva de restitución celular, particularmente su pendiente, está directamente relacionada a la ocurrencia de alternancias. Esto último nos lleva a una segunda aplicación posible que tiene que ver con la relación que puede existir entre las ya conocidas alternancias de la onda T [42, 43] y las alternancias del APD, las cuales podrían tener una explicación por medio de la relación de restitución.
AGRADECIMIENTOS
Se agradece enormemente el apoyo de la Dirección de Investigación y Desarrollo (DID) de la Universidad Austral de Chile por medio del financiamiento del proyecto s-2009-28. Se agradece igualmente a Víctor Alcafuz, Juan Pablo Arias y Alejandro Bertín que con sus tesis de pregrado aportaron significativos aportes a los avances de este trabajo.
REFERENCIAS
[1]. Malmivuo J., Plonsey R. Bioelectromagnetism: Principles and Aplication of Bioelectric and Biomagnetic Fields. Oxford University Press, 1995. Capítulo 6, 165-177. [ Links ]
[2]. Sörnmo L., Laguna P. Bioelectrical signal processing in cardiac and neurological applications. Elsevier, 2005. Capítulo 6, 411-452. [ Links ]
[3]. Arnold L., Page J., Attwell D., Cannell M., Eisner D. The dependence on heart rate of the human ventricular action potential duration. Cardiovascular research, 313, 547-551, 1981. [ Links ]
[4]. Attwell D., Cohen I., Eisner D. The effects of heart rate on the action potential of guinea-pig and human ventricular muscle. The Journal of Physiology, 16, 439-461, 1982. [ Links ]
[5]. Fossa A., Wisialowski T., Crimin K. QT prolongation modifies dynamic restitution and hysteresis of the beat-to-beat QTTQ interval relationship during normal sinus rhythm under varying states of repolarization. Journal of Pharmacology and Experimental Therapeutics, 316(2), 498-506, 2006. [ Links ]
[6]. Fossa A., Wisialowski T., Crimin K., Wolfgang E., Couderc J.P., Hinterseer M., Kaab S., Zareba W., Badilini F., Sarapa N. Analyses of dynamic Beat-to-Beat QT-TQ interval (ECG restitution) changes in humans under normal sinus rhythm and prior to an event of Torsades de Pointes during QT prolongation caused by Sotalol. Annals of noninvasive electrocardiology, 12(4), 338-348, 2007. [ Links ]
[7]. Illanes Manriquez A., Zhang Q., Medigue C., Papelier Y., Sorine M. Electrocardiogram-based restitution curve. Proceedings of the Computers in Cardiology, Valencia, Spain, 33, 493-496, 2006. [ Links ]
[8]. Panfilov, A. V. (ed.) et al. Forward and inverse problems in electrocardiography. Computational biology of the heart. Workshop on Whole Heart Modeling, 11th-13th February 1994, Utrecht, the Netherlands. Chichester: Wiley. 295-343, 1997. [ Links ]
[9]. MacLeod R., Brooks D. Recent progress in inverse problems in electrocardiology. IEEE Engineering in Medicine and Biology, 17(1), 73-83, January/February 1998. [ Links ]
[10]. Gulrajani R. The forward and inverse problems of electrocardiography: Gaining a better qualitative and quantitative understanding of the heart's electrical activity. IEEE Engineering in Medicine and Biology, 17(5), 84-122, September/October 1998. [ Links ]
[11]. Armoundas A., FeldmanA., Mukkamala R., Cohen R. A single equivalent moving dipole model: An efficient approach for localizing sites of origin of ventricular electrical activation. Annals of Biomedical Engineering, 31, 564-576, 2003. [ Links ]
[12]. Ghodrati A., Brooks D., Tadmor G., MacLeod R. Wavefrontbased models for inverse electrocardiography. IEEE Transaction on Biomedical Engineering, 53(9), 1821-1831, 2006. [ Links ]
[13]. Nielsen B., Cai X., Lysaker M. On the possibility for computing the transmembrane potential in the heart with a one shot method: An inverse problem. Mathematical Biosciences, 210, 523-553, 2007. [ Links ]
[14]. Franz M., Schaefer J., Schottler M., Seed W., Noble M. Electrical and mechanical restitution of the human heart at different rates of stimulation. Circulation, 53, 815-822, 1983. [ Links ]
[15]. Elharrar V., Surawicz B. Cycle length effect on restitution of action potential duration in dog cardiac fibers. American Journal of Physiologie, 244, H782-H792, 1983. [ Links ]
[16]. Franz M., Swerdlow C., Liem B., Schaefer J. Cycle length dependence of human action potential duration in vivo. The American Society for Clinical Investigation, 82, 972-979, 1988. [ Links ]
[17]. Koller M., Riccio M., Gilmour R. Dynamic restitution of action potential duration during electrical alternans ans ventricular fibrillation. American Journal of Physiology, 275(2), H1635- H1642, 1998. [ Links ]
[18]. Koller M., Maier S., Gelzer A., Bauer W., Meesmann M., Gilmour R. Altered dynamics of action potential restitution and alternans in humans with structural heart disease. Circulation, 112, 1542-1548, 2005. [ Links ]
[19]. Tolkacheva E., Schaeffer D., Gauthier D., Mitchell C. Analysis of the Fenton-Karma model through an approximation by a onedimensional map. Chaos, 12(4), 1034-1042, 2002. [ Links ]
[20]. Mitchell C., Schaeffer D. A two-current model for de dynamics of cardiac membrane. Bulletin of Mathematical Biology, 65, 767-793, 2003. [ Links ]
[21]. Jordan P., Christini D. Determining the effects of memory and action potential duration alternans on cardiac restitution using a constant-memory restitution protocol. Physiological measurements, 25, 1013-1024, 2004. [ Links ]
[22]. Nolasco J., Dahlen R. A graphic method for the study of alternation in cardiac action potentials. Journal of Applied Physiology, 25, 191-196, 1968. [ Links ]
[23]. Karma A. Electrical alternans and spiral wave breakup in cardiac tissue. Chaos, 4(3), 461-472, 1994. [ Links ]
[24]. Watanabe M., Otani N., Gilmour R. Biphasic restitution of action potential duration and complex dynamics in ventricular myocardium. Circulation Research, 76, 915-921, 1995. [ Links ]
[25]. Watanabe M., Fenton F., Evans S., Hastings H., Karma A. Mechanisms for discordant alternans. Journal of Cardiovascular Electrophysiology, 12(2), 196-206, 2001. [ Links ]
[26]. Franz M. The electrical restitution curve revisited: Steep or flat slope - which is better. Journal of Cardiovascular Electrophysiology, 14(10), S140-S147, October 2003. [ Links ]
[27]. Cain J., Tolkacheva E., Shaeffer D., Gauthier D. Rate-dependent propagation of cardiac action potentials in a one-dimensional fiber. Physical Review, 70, 061906, 2004. [ Links ]
[28]. Otani N., Gilmour R. Memory models for the electrical properties of local cardiac systems. J. Theor. Biol., 187, 409-436, 1997. [ Links ]
[29]. Gilmour R., Otani N., Watanabe M. Memory and complex dynamics in cardiac Purkinje fibers. American Journal of Physiology, 272, H1826-H1832, 1997. [ Links ]
[30]. Tolkacheva E., Schaeffer D., Gauthier D., Krassowska W. Condition for alternans and stability of the 1:1 response pattern in a "memory" model of paced cardiac dynamics. Physical Review E, 67, 031904, 2003. [ Links ]
[31]. Illanes A., Sérandour G. Modelo paramétrico de actividad eléctrica celular cardiaca estimado mediante electrocardiograma. Terceras Jornadas de Ingeniería Biomédica JCIB 2012, Viña del Mar, Chile, 2012. [ Links ]
[32]. Boyett M., Jewell B. A study of the factors responsible for rate-dependent shortening of the action potential in mammalian ventricular muscle. Journal of Physiology, 285, 359-380, 1978. [ Links ]
[33]. Guevara M., Ward G., Shrier A., Glass L. Electrical alternans and period doubling bifurcations. Computers in Cardiology, 167-170, 1984. [ Links ]
[34]. Abildskov J. The sequence of normal recovery of excitability in the dog heart. Circulation research, 52, 442-446, 1975. [ Links ]
[35]. Watanabe T., Rautaharju P., McDonald T. Ventricular action potentials, ventricular extracellular potentials, and ECG of guinea-pig. Circulation Research, 57, 362-373, 1985. [ Links ]
[36]. Médigue C., Papelier Y., Bise S., Sorine M. Short term control of the cardiovascular system: Assessment with the isometric handgrip exercise. INRIA, Tech. Rep., 2004. [ Links ]
[37]. Matlab. The Mathwork Inc., Natick, Massachusetts. http://www.mathworks.com/. [ Links ]
[38]. Scilab: The open source platform for numerical computation, http://www.scilab.org/. [ Links ]
[39]. Illanes Manriquez A., Zhang Q. An algorithm for QRS onset and offset detection in single lead electrocardiogram records. Proceedings of the 29th Annual International Conference of the IEEE EMBS, Lyon, France, 29, 541-544, 2007. [ Links ]
[40]. Chacón F., Illanes-Manriquez A. Evaluación de un algoritmo simple de detección de onda R con bases de datos estándares. Segundas Jornadas Chilenas de Ingeniería Biomédica, Viña del Mar, Chile, 2009. [ Links ]
[41]. Zhang Q., Illanes Manriquez A., Médigue C., Papelier Y., Sorine M. An algorithm for robust and efficient location of T-wave ends in electrocardiograms. IEEE Transaction on Biomedical Engineering, 53(12), 2544-2552, 2006. [ Links ]
[42]. Chow T., Saghir S., Bartone C., Goebel M., Schneider J., Booth T., Chan PS. Usefulness of microvolt T-wave alternans on predicting outcome in patients with ischemic cardiomyopathy with and without defibrillators. Am J Cardiol, 100(4), 598-604, 2007. [ Links ]
[43]. Bloomfield D., Bigger J., Steinman R., Namerow P., Parides M., Curtis A., Kaufman E., Davidenko J., Shinn T., Fontaine J. Microvolt T-wave alternans and the risk of death or sustained ventricular arrhythmias in patients with left ventricular dysfunction. J Am Coll Cardiol, 47(2), 456-63, 2005. [ Links ]