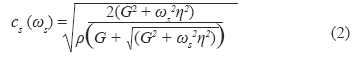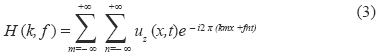IN VIVO SWINE KIDNEY VISCOELASTICITY DURING ACUTE GRADUAL DECREASE IN RENAL BLOOD FLOW: PILOT STUDY

VISCOELASTICIDAD RENAL DURANTE LA DISMINUCIÓN GRADUAL DE FLUJO SANGUÍNEO EN UN MODELO PORCINO IN VIVO: ESTUDIO PILOTO

Carolina Amador^1,2, Matthew Urban¹, Randall Kinnick¹, Shigao Chen¹, James F. Greenleaf¹

1 Department of Physiology & Biomedical Engineering, Mayo Clinic, Rochester, United States.
2 Dirección para correspondencia: amadorcarrascal.carolina@mayo.edu.

Recibido 2 de mayo de 2013. Aprobado 28 de mayo de 2013. En discusión hasta el 1 de junio de 2013

ABSTRACT

Elasticity imaging methods have been used to study kidney mechanical properties and have demonstrated that the kidney elastic modulus increases with disease state. However, studies in swine suggest that kidney elastic modulus is also affected by hemodynamic variables. A newly emerging method called Shearwave Dispersion Ultrasound Vibrometry (SDUV) offers a tool to determine renal elasticity and viscosity in vivo. The purpose of this study was directed toward evaluating the feasibility of SDUV for in vivo measurements of healthy swine kidney during acute gradual decease of renal blood flow. In this study in vivo SDUV measurements were made on a group of 5 normal swine kidneys at baseline renal blood flow (RBF) and 25, 50, 75 and 100% decrease in RBF. The shear elastic modulus at full baseline was 7.04 ± 0.92 kPa and 3.48 ± 0.20 kPa at 100% decrease in RBF. The viscosity did not change between baseline (2.23 ± 0.33 Pa•s) and 100% decrease in RBF (2.03 ± 0.32 Pa•s). The data from this study indicates that other variables such as local blood flow, pressure and volume as well as method accuracy need to be measured to illustrate the relationship between shear elasticity and viscosity associated with acute kidney processes.

KEY WORDS: Renal cortex, elasticity, viscosity, ultrasound, medical imaging.

RESUMEN

Métodos de imágenes de elasticidad se han utilizado para estudiar las propiedades mecánicas renales y han demostrado que el módulo elástico de los riñones del aumenta con el estado de enfermedades renales. Sin embargo, estudios en cerdos sugieren que el riñón módulo elástico también se ve afectada por las variables hemodinámicas. Un método emergente llamado Shearwave Dispersion Ultrasound Vibrometry (SDUV) ofrece una herramienta para determinar la elasticidad y la viscosidad renal. El propósito de este estudio se dirige a la evaluación de la viabilidad de SDUV para mediciones las propiedades viscoelasticas del riñón saludable durante variación aguda del flujo sanguíneo renal. En este estudio el método SDUV se realizó en un grupo de 5 riñones porcinos normales al inicio del flujo sanguíneo renal (RBF) basal y 25, 50, 75 y 100% de disminución en el RBF. El módulo elástico basal fue de 7,04 ± 0,92 kPa y 3,48 ± 0,20 kPa a 100% de disminución del RBF. La viscosidad no cambió entre el momento basal (2,23 ± 0,33 Pa • s) y el 100% de disminución del RBF (2,03 ± 0,32 Pa • s). Los datos de este estudio indican que variables tales como el flujo local de sangre, la presión y el volumen así como el método exactitud deben ser medidos para ilustrar la relación entre la elasticidad y la viscosidad asociada con los procesos renales agudos.

PALABRAS CLAVE: Corteza renal, elasticidad, viscosidad, ultrasonido, imágenes médicas.

I. INTRODUCTION

Elasticity imaging is an emerging imaging modality that has the potential to assess kidney state in chronic kidney disease (CKD) by using the mechanical properties of kidney as the contrast mechanism in images. CKD encompasses a long-term decrease in renal function. Progressive CKD leads to the destruction of kidney parenchyma and ultimately to end-stage renal disease (renal failure), a condition that requires dialysis or kidney transplant [1].

Various functional measurements such as biomarkers, renal biopsies and noninvasive imaging methods are used to assess kidney function in management of CKD. However, there is still a need for fast, low cost noninvasive tool capable of assessing kidney function in the early stages of CKD. Several elasticity imaging methods, such as elastography, acoustic radiation force imaging (ARFI), transient elastography (TE), magnetic resonance elastography (MRE), supersonic shear imaging (SSI) and shearwave dispersion ultrasound vibrometry (SDUV), have been used to study kidney mechanical properties [2-11]. For instance, a study in rats has shown that stiffness in the renal cortex increases after 2 and 4 week exposures to ethylene glycol which causes nephrocalcinosis, an end-stage renal disease [12]. Elasticity imaging methods have demonstrated that elasticity of the kidney changes with disease state and changes enough to be detected.

The kidney, like many other soft tissues, exhibits viscoelastic behavior, that is, the kidney has both elastic and viscous characteristics [13]. Measurements of the elastic component can be biased higher than the actual values if viscoelastic materials are treated as elastic materials [6, 14]. Therefore, to fully characterize the kidney, measurements of the elastic and viscous components of the tissue need to be measured. Tissue viscoelastic properties are usually measured in a model dependent manner by mean of fitting a rheological model to shear wave speed dispersion [15, 16]. The Voigt model has been shown to be appropriate for describing viscoelastic properties of tissue in the low frequency range (50-500 Hz) [17, 18]. In current practice, elastography and ARFI are useful approaches, but they do not provide a quantitative measure of tissue elastic moduli. TE and MRE are capable of quantifying tissue elastic moduli but not the viscous component. SSI can provide maps of elastic moduli and viscosity, but specialized hardware is necessary to implement this method. SDUV is capable of providing quantitative measurements of tissue viscosity, in addition to elastic modulus. SDUV has been used to characterize swine kidney mechanical properties in vitro [10, 19].

The kidney is a highly vascularized organ, up to 25% of its volume may be attributed to its hemodynamics. The effects of hemodynamic alterations on tissue viscoelasticity have not been extensively studied [9, 11, 20]. In studies in swine, the renal artery was occluded in progressive steps, and the cortical and medullary stiffness decreased as a result of decreased perfusion [9], in contrast when the renal vein is occluded the cortical and medullary stiffness increased [11]. Similarly, studies in canine livers have shown increase stiffness with changes in interstitial pressure [20].

SDUV potentially offers an in vivo tool to assess the physiological changes of the kidney and to monitor the development of CKD. The purpose of this study was therefore directed toward evaluating the feasibility of SDUV for in vivo measurements of viscoelasticity in healthy swine kidney. Moreover, in this study SDUV was used to measure kidney viscoelastic properties during acute gradual decrease of renal blood flow. For this purpose, shearwave dispersion was studied by exciting shear waves in the renal cortex with a mechanical actuator and with acoustic radiation force.

II. MATERIALS AND METHODS

Animal experiments were reviewed and approved by the Mayo Clinic Institutional Animal Care and Use Committee. Five domestic female pigs were used in this study. For all studies, pigs were anesthetized (telazol 5 mg/ kg and xylazine 2 mg/kg) and maintained with mechanical ventilation of 1-2% isoflurane in room air. An ear vein catheter was introduced for saline infusions (5 mL/min). A catheter was placed in one carotid artery for monitoring mean arterial pressure (MAP). An ultrasonic Doppler flow meter (Transonic System, T206, probe 3RB429) was placed on the right renal artery for continuous monitoring of the renal blood flow (RBF). A pneumatic inflatable vascular occluder was placed on the right renal artery proximal to the Doppler flow meter.

2.1 Shearwave dispersion ultrasound vibrometry (SDUV)

Shearwave dispersion ultrasound Vibrometry (SDUV) is a method that quantifies both tissue shear elasticity and viscosity by evaluating dispersion of shear wave propagation speed over a certain bandwidth [15, 21]. In this study, shear waves are excited by an external mechanical actuator and by acoustic radiation force.

2.2 Shear wave excitation with mechanical actuator

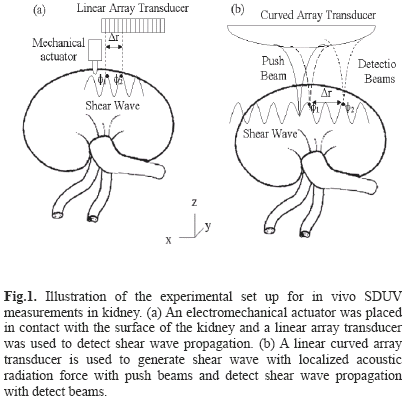
Three animals were studied with this SDUV implementation. The right kidney was exteriorized through a small flank incision. An electromechanical actuator (V203, Ling Dynamic Systems Limited, Hertfordshire, UK) was placed in contact with the surface of the kidney to vibrate the kidney and create propagating shear waves. The electromechanical actuator was driven by a single frequency signal in the range of 100 Hz to 400 Hz by 50 Hz increments. This signal was amplified and applied to the electromechanical actuator. The motion was measured using a high-frame rate mode that acquired 7 A-lines with 0.9 mm A-line separation at a frame rate of about 2500 frames per second (fps) using a Sonix RP ultrasound scanner equipped with a L14-5/38 linear array transducer (Ultrasonix Medical Corp. Richmond, BC, Canada). The electromechanical actuator was placed near one end of the transducer, Fig. 1. Ultrasound echoes were processed by the previously described cross-correlation method to estimate displacement [22]. A temporal Fourier transform (FFT) was performed to the displacement estimates and phase gradients were taken from the FFT signal at the frequency of interest.

The shear wave speed at different frequencies is estimated from its phase measured at least at 2 locations separated by Δr along its traveling path:

where Δø_s = ø₂ - ø₁ is the phase gradient over the traveled distance Δr. To estimate viscoelastic properties from shear wave dispersion, a rheological model is required. The most common rheological models are the Kelvin - Voigt and the Maxwell model. The Kelvin - Voigt model has been shown to be appropriate for describing viscoelastic properties of tissue in the low frequency range (50-500 Hz) [16, 23] and it has been used to characterize in vitro swine kidney mechanical properties with SDUV [10, 19]. For a viscoelastic, homogenous, isotropic material, the Kelvin - Voigt model relates the shear wave propagation speed, c_s, and the frequency of shear wave, ω_s by [17]

where ρ, G and η are the density, shear elastic modulus and viscosity of the medium, respectively. The shear wave speed was then estimated with Equation 1 and shear wave speeds between 100 Hz and 400 HZ were fitted by Equation 2 to solve for the shear elastic modulus and viscosity. Shear wave phase velocity was estimated at each excitation frequency over a region of interest (ROI), approximately 7.2 mm along x-axis and 5 mm along z-axis, in the renal cortex at full baseline renal blood flow, 25%, 50%, 75% and 100% decrease in baseline renal blood flow.

2.3 Shear wave excitation with acoustic radiation force

External mechanical excitation creates single frequency shear waves to characterize viscoelastic behavior using shear wave dispersion. A limitation of this type of excitation is that the modulation frequency has to be changed multiple times to evaluate dispersion over a significant bandwidth. To overcome this limitation, acoustic radiation force is used to generate shear waves over a certain bandwidth with a single impulse excitation.

SDUV has been implemented on a Verasonics V-1 system. Two animals were studied with this SDUV implementation, with a setup that used a curved linear array transducer (C4-2, Philips Healthcare, Andover, MA), Fig. 1(b). The Verasonics V-1 ultrasound system (Verasonics, Redmond, WA) is a programmable ultrasound research platform that has 128 independent transmit channels and 64 receive channels. The system is integrated around a software-based beamforming algorithm that performs a pixel-oriented processing algorithm. This algorithm facilitates conventional and high frame rate imaging.

The curved linear array transducer was partially located in the abdominal cavity through a small flank incision. A 3 MHz, 331 µs duration push beam was transmitted and focused in the renal cortex to generate shear waves in the medium. The shear wave propagation was measured with the same transducer with 2 kHz flash imaging and plane wave compounding imaging technique [24]. A set of 3 plane waves with different emission angles were transmitted at 6 kHz pulse repetition frequency (PRF). By coherently compounding each set of 3 plane waves, a compound image PRF of 2 kHz was produced. The push causes shear displacements outward of the focal region in the +x and -x directions. The spatial resolution in x-direction and z-direction were 0.25 mm and 0.5 mm respectively. The field of view (FOV) was 40 mm in x-direction and 60 mm in z-direction. Local tissue displacements are estimated using 1-D autocorrelation between two compounded images [25]. Shear wave phase velocity was estimated by previously described twodimensional Fourier transform method [26, 27]. A twodimensional (2D) Fourier transform (FFT) is performed to the displacement estimates:

where u_z(x,t) is the estimated displacement in z-axis, which is a function of distance along x-axis and time, k is the wave number and f is the temporal frequency.

The 2D-FFT analysis were used to estimate shear wave phase velocities as a function of frequency at full baseline renal blood flow, 25%, 50%, 75% and 100% decrease in baseline renal blood flow.

2.4 Statistical analysis

Results are reported as mean ± standard deviation. The number of samples, repetitions and size of regions of interest (ROI) were made on the basis of the data and the degree of their scatter and reproducibility. Univariate ANOVA was used to test for statistically significant differences among variables for the different experiments. Statistical significance for all tests was accepted for p ≤ 0.05.

III. RESULTS

Table 1 shows the characteristics of the experimental animals. All five animals had similar body weight.

Table 1

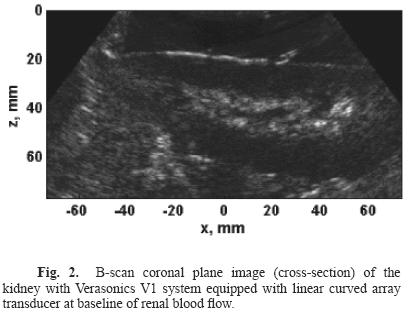
B-scan coronal plane images (cross-section) were acquired with the Verasonics V1 ultrasound system equipped with a curved array transducer at baseline of renal blood flow, Fig. 2.

The estimated tissue displacement from crosscorrelation method [22] generated by 100 Hz harmonic excitation at baseline of renal blood flow is illustrated in Fig. 3(a). The magnitude of the temporal Fourier transform of the estimated displacement from Fig. 3(a) is illustrated in Fig. 3(b). The estimated shear wave phase gradient estimated using Fourier transform analysis at 100 Hz, 200 Hz, 300 Hz and 400 Hz excitation for baseline renal blood flow is shown in Fig. 3(c). The mean shear wave phase velocity estimated from Equation 1 as a function of frequency for baseline renal blood flow is illustrated in Fig. 3(d).

Figure 3

Shear wave dispersion (shear wave phase velocity as a function of frequency) were measured from three repetitions using mechanical excitation for animals 1, 2 and 3, Fig. 4. The color bars represent baseline renal blood flow, 25, 50, 75 and 100% decrease in baseline renal blood flow respectively.

Figura 4

Fig. 5(a) illustrates displacement estimates, from 1D autocorrelation method [25], generated by acoustic radiation force toneburst applied at baseline of renal blood flow. The push at x = 0 causes shear motion outward the focal region in the +x and -x directions. Displacement estimates as a function of time over 7.4 mm to 9.5 mm in +x direction are shown in Fig. 5(b). The wave number - frequency diagram from 2D Fourier transform of tissue displacement estimates outward the focal region in the +x direction is shown in Fig. 5(c). Shear wave phase velocity as a function of frequency estimated by 2D-FFT method [27] for baseline renal blood flow is illustrated in Fig. 5(d).

Figure 5

One of the advantages of the 2D Fourier transform method is the high resolution in frequency as illustrated in Fig. 5(d). Shear wave phase velocity, for frequencies between 100 Hz and 400 Hz with 50 Hz increments, from three repeated measurements using acoustic radiation force toneburst excitation for animals 4 and 5 is shown in Fig. 6. The color bars represent baseline renal blood flow, 25, 50, 75 and 100% decrease in baseline renal blood flow respectively.

Figure 6

The shear wave speed of the group of five animals (mean ± standard deviation) is statistically significant different at each occlusion state between 100 Hz and 400 Hz (p<0.001), Fig. 7. Moreover, during acute renal blood flow reduction, a decrease in shear phase velocity at low frequency (100 Hz) was observed in the group of animals (p<0.02).

On the other hand, there is not statistically significant difference in shear wave speed from all occlusion periods at 400 Hz (p = 0.67).

Shear elastic modulus and viscosity of the group of five animals (mean ± standard deviation) as a function of acute gradual decrease in renal blood flow is illustrated in Fig. 8. The shear elastic modulus of the group of five animals (mean ± standard deviation) is statistically significant different at each occlusion state (p<0.01). On the other hand, there is not a statistically significant difference in viscosity from all occlusion periods (p = 0.90).

Figure 8

B-scan coronal plane images (cross-section) acquired with the Verasonics V1 ultrasound system equipped with a curved array transducer at base line renal blood flow and 100% decrease in baseline renal blood flow in one kidney is illustrated in Fig. 9.

Figure 9

Fig. 10(a) illustrate the cortical thickness (geometric distance between red lines shown in Fig. 9) measured from B-scan images over 40 mm in x direction. Cortical thickness as a function of acute gradual decrease in renal blood flow is illustrated in Fig. 10(b).

Figure 10

IV. DISCUSSION

This study reports in vivo quantitative measurements of shear elastic modulus and viscosity of healthy swine kidneys measured by SDUV using two experimental configurations, a mechanical actuator and acoustic radiation force. Moreover, swine kidney shear elastic modulus and viscosity were measured during acute gradual decrease of renal blood flow.

Shear wave dispersion (shear wave phase velocity as a function of frequency) shown in Fig. 3(d) and Fig. 5(d) was consistent between shear waves generated by mechanical actuator at a single frequency (pure-tone shear waves) and shear waves generated by acoustic radiation force with an impulse (multi-tone shear waves). The signal-to-noise ratio (SNR), defined as the ratio of mean to standard deviation of measurements, for the shear wave phase velocities excited with mechanical actuator (Fig. 4) was 3 times higher than the shear wave phase velocities from acoustic radiation force excitation (Fig. 6). It is expected that when acoustic radiation force is applied through tissue layer (skin, fat, muscle) before reaching the organ of interest, shear wave motion will decrease due to phase aberration and attenuation leading to smaller SNR. A more detailed comparison between multi-tone approach and single-tone approach in gelatin phantoms was previously reported by Chen et al. [15] and there were no significant differences between shear elastic modulus and viscosity estimations.

To estimate viscoelastic properties, a model needs to be fit to the shear wave dispersion. In this study, the Voigt model was used to fit shear wave dispersion to estimate shear elastic modulus and viscosity. The Voigt model has been previously used to study in vitro kidney viscoelastic properties [10, 19]. Although this rheological model assumes homogeneous and isotropic material, an in vitro study by our group shows a fairly good fit to kidney shear wave dispersion [18]. The shear elastic modulus of the group of 5 animals shown in Fig. 8(a) was highest at baseline renal blood flow, once the renal blood flow was decreased by 25% of baseline, the shear elastic moduli decreased by larger proportion when compared to 50, 75, and 100% decreased of baseline renal blood flow, refer to Fig. 8(a). It has been reported by Rognant et al. [28] that a 25% decrease of renal blood flow from baseline is equivalent to approximately 70% acute renal artery stenosis, therefore the decrease in renal blood flow from 25% to 100% of baseline would be equivalent to a very small percentage in renal artery stenosis, which may be the reason why the shear elastic moduli did not change much during 25, 50, 75 and 100% decrease in baseline renal blood flow.

The shear elastic modulus measurements presented in this study are rather similar to previous estimates in the literature. For instance, an MRE study by Warner et al reported in vivo swine kidney shear elastic modulus of 3 kPa, and it also reported a decrease in shear elastic modulus with acute decrease in renal blood flow [9]. Changes in kidney shear modulus by altering the blood from the renal vein and urinary have also been reported by Gennisson et al [11], where occluding the renal vein caused increase in kidney shear modulus and the increase of urinary pressure caused increase in shear modulus. The hemodynamic effects in tissue mechanical properties have also been studied in other soft tissue like the liver. Rotemberg et al reported shear wave speed estimates in excised canine liver that were pressurized, in this study the shear wave speed variations are alluded to nonlinear material characteristics [20]. These previous studies did not consider tissue viscosity. If viscosity is not taken into account, measurements of shear stiffness can be biased higher than their actual values [6, 14]. Tissue viscosity is an understudied quantity but it may provide important information about tissue state.

The kidney viscosity measured in this study did not change as a function of renal blood flow, Fig. 8(b). The variations in shear elastic modulus and viscosity at each renal blood flow period (refer to Fig. 8) could be attributed to the small number of shear wave phase velocity measurements for the mechanical actuator method (singletone approach), refer to Fig. 3(d). To illustrate this, when fitting the Voigt model to 7 measurements of shear wave speed (e.g. 100 Hz to 400 Hz by 50 Hz increments in Fig. 5), the shear elastic modulus is 3.47 kPa and viscosity is 1.79 Pa•s, compared to 3.83 kPa and 1.75 Pa•s from fitting 30 shear wave speed measurements. Because SDUV had been implemented in the Verasonics ultrasound system, SDUV measurements are acquired with high temporal and spatial resolution, by means of shear wave detection, and as a consequence it allows the use of the two-dimensional Fourier transform method, which then estimates shear wave phase velocity over a large bandwidth with high resolution. Although the accuracy of shear wave phase velocity estimates from 2DFFT method was not evaluated in this study, the 2DFFT method is a robust method that is commonly used for seismic applications [27] and it has been used to study shear wave propagation modes in arteries [26].

Because viscosity is a relatively unexplored parameter, there remains a question about how accurate the viscosity estimates are. In this study, we did not evaluate the precision of SDUV for in vivo measurements; therefore it is difficult to separate method variability to other parameter such as tissue heterogeneity, local blood pressure and blood volume, which unfortunately were also not measured. In a report by Schmeling, et al. the viscosity in the left ventricular wall of the heart during the diastolic phase of the cardiac cycle increased during occlusion of the left anterior descending coronary artery in animals that were reperfused and not reperfused [29]. During reperfusion, the viscosity returned to baseline in animals that recovered from the stunning while the increase in viscosity persisted throughout reperfusion in animals that did not recover. Viscosity was shown to increase in both ischemic and nonischemic regions of the ventricular wall. Viscosity may be an indicator of tissue damage (for instance, ischemia or acute kidney injury). A more comprehensive study is needed to evaluate such hypothesis specifically. The high variability in the viscosity estimates for this in vivo SDUV kidney study could be associated to errors in phase estimates at high frequencies, which are expected because displacement amplitude decreases at high frequencies (shear wave attenuates faster). Urban et al. reported a study where different parameters that affect the performance of SDUV were evaluated [30]. Although the errors associated with phase estimate are expected to be small, these errors affect shear wave phase velocity estimates.

The B-mode images at baseline and 100% decrease of baseline renal blood flow illustrate a change in renal volume, refer to Fig. 10(a). Moreover, there is a relatively large difference between cortical thickness at baseline and at a 100% decrease of baseline renal blood flow, Fig. 10(b). These are images of just one section of the kidney; therefore, it is difficult to state that indeed the kidney volume is changing, especially when urine and blood volume were not measured. Nonetheless, Warner et al reported statistically significant change in kidney volume from baseline compared to 100% decrease in baseline blood flow [9].

Finally, although this study demonstrates the feasibility of SDUV to study in vivo exposed kidney viscoelasticity, there may be some limitations when studying the kidney transcutaneously. For instance, because the kidney is a highly perfused organ, it is important to study the hemodynamic effects in renal viscoelasticity independent of renal disease. In this study, only renal blood flow was monitored, therefore, future studies should assess other parameters such as blood pressure, blood volume, urine volume, perfusion pressure, glomerular filtration rate, diuresis, etc.

V. CONCLUSION

Shearwave dispersion ultrasound vibrometry provides a fast, low cost non-invasive tool to measure not only tissue elasticity but also tissue viscosity. It has the potential to monitor progression of disease with less risk, potential sampling error and cost inherent to biopsies. In this study we showed that shear elastic moduli is affected by renal blood flow. Moreover, the data from this study indicates that other variables such as local blood flow, pressure, and volume as well as method accuracy need to be measured to illustrate the relationship between shear elasticity and viscosity with acute and chronic kidney processes. Nonetheless, the ability of SDUV to detect changes in elastic moduli related to blood flow represent a novel method to measure kidney hypoperfusion.

ACKNOWLEDGMENTS

The project described was supported by Grant Number DK082408 from the NIH. The content is solely the responsibility of the authors and does not necessarily represent the official views of the NIH. Disclosure: Mayo Clinic and some authors have financial interest in the technology. Patents were issued and the technology has been licensed for research and development.

REFERENCES

[1]. Y. H. Liu, "Renal fibrosis: New insights into the pathogenesis and therapeutics," Kidney International, 69, 213-217, January 2006.         [ Links ]

[2]. S. Y. Emelianov, M. A. Lubinski, W. F. Weitzel, R. C. Wiggins, A. R. Skovoroda, and M. Odonnell, "Elasticity imaging for early detection of renal pathology," Ultrasound in Medicine and Biology. 21, 871-883, 1995.         [ Links ]

[3]. K. R. Nightingale, M. L. Palmeri, R. W. Nightingale, and G. E. Trahey, "On the feasibility of remote palpation using acoustic radiation force," Journal of the Acoustical Society of America. 110, 625-634, July 2001.         [ Links ]

[4]. B. J. Fahey, K. R. Nightingale, R. C. Nelson, M. L. Palmeri, and G. E. Trahey, "Acoustic radiation force impulse imaging of the abdomen: Demonstration of feasibility and utility," Ultrasound in Medicine and Biology, 31, 1185-1198, September 2005.         [ Links ]

[5]. R. Arndt, S. Schmidt, C. Loddenkemper, M. Grünbaum, W. Zidek, M. Van Der Giet, and T. H. Westhoff, "Noninvasive evaluation of renal allograft fibrosis by transient elastography - a pilot study," Transplant International. 23, 871-877, 2010.         [ Links ]

[6]. S. A. Kruse, J. A. Smith, A. J. Lawrence, M. A. Dresner, A. Manduca, J. F. Greenleaf, and R. L. Ehman, "Tissue characterization using magnetic resonance elastography: preliminary results," Physics in Medicine and Biology, 45, 1579- 1590, June 2000.         [ Links ]

[7]. N. S. Shah, S. A. Kruse, D. J. Lager, G. Farell-Baril, J. C. Lieske, B. F. King, and R. L. Ehman, "Evaluation of renal parenchymal disease in a rat model with magnetic resonance elastography," Magnetic Resonance in Medicine, vol. 52, pp. 56-64, July 2004.         [ Links ]

[8]. M. Yin, J. Chen, K. J. Glaser, J. A. Talwalkar, and R. L. Ehman, "Abdominal magnetic resonance elastography," Topics in Magnetic Resonance Imaging. 20, 79-87, 2009.         [ Links ]

[9]. L. Warner, M. Yin, K. J. Glaser, J. A. Woollard, C. A. Carrascal, M. J. Korsmo, J. A. Crane, R. L. Ehman, and L. O. Lerman, "Noninvasive In Vivo Assessment of Renal Tissue Elasticity During Graded Renal Ischemia Using MR Elastography," Investigative Radiology. 46, 509-514, 2011.         [ Links ]

[10]. C. Amador, M. W. Urban, L. V. Warner, and J. F. Greenleaf, "In vitro renal cortex elasticity and viscosity measurements with shearwave dispersion ultrasound vibrometry (SDUV) on swine kidney," in Engineering in Medicine and Biology Society, 2009. EMBC 2009. Annual International Conference of the IEEE, 2009, 4428-4431.         [ Links ]

[11]. J. L. Gennisson, N. Grenier, C. Combe, and M. Tanter, "Supersonic shear wave elastography of in vivo pig kidney: influence of blood pressure, urinary pressure and tissue anisotropy," Ultrasound in Medicine and Biology. 38, 1559-1567, September 2012.         [ Links ]

[12]. N. S. Shah, S. A. Kruse, D. J. Lager, G. Farell-Baril, J. C. Lieske, B. F. King, and R. L. Ehman, "Evaluation of renal parenchymal disease in a rat model with magnetic resonance elastography," Magn Reson Med. 52, 56-64, July 2004.         [ Links ]

[13]. Y. Fung, Biomechanics: mechanical properties of living tissues: Springer-Verlag, 1993.         [ Links ]

[14]. C. Amador, M. W. Urban, S. Chen, Q. Chen, K. An, and J. F. Greenleaf, "Shear Elastic Modulus Estimation From Indentation and SDUV on Gelatin Phantoms," Biomedical Engineering, IEEE Transactions on, 58, 1706-1714, 2011.         [ Links ]

[15]. S. Chen, M. Urban, C. Pislaru, R. Kinnick, Z. Yi, Y. Aiping, and J. Greenleaf, "Shearwave dispersion ultrasound vibrometry (SDUV) for measuring tissue elasticity and viscosity," IEEE Transactions on Ultrasonics Ferroelectrics and Frequency Control, 56, 55-62, 2009.         [ Links ]

[16]. T. Deffieux, G. Montaldo, M. Tanter, and M. Fink, "Shear Wave Spectroscopy for In Vivo Quantification of Human Soft Tissues Visco-Elasticity," IEEE Transactions on Medical Imaging, 28, 313-322, March 2009.         [ Links ]

[17]. S. Catheline, J. L. Gennisson, G. Delon, M. Fink, R. Sinkus, S. Abouelkaram, and J. Culioli, "Measurement of viscoelastic properties of homogeneous soft solid using transient elastography: An inverse problem approach," Journal of the Acoustical Society of America. 116, 3734-3741, December 2004.         [ Links ]

[18]. C. Amador, M. W. Urban, S. Chen, and J. F. Greenleaf, "Shearwave Dispersion Ultrasound Vibrometry (SDUV) on swine kidney," IEEE Trans. Ultrason., Ferroelect., Freq. Contr. 58, 2608-2620, In press. 2011.         [ Links ]

[19]. C. Amador, M. W. Urban, J. F. Greenleaf, and L. V. Warner, "Measurements of swine renal cortex shear elasticity and viscosity with Shearwave Dispersion Ultrasound Vibrometry (SDUV)," in Ultrasonics Symposium (IUS), 2009 IEEE International, 2009, 491-494.         [ Links ]

[20]. V. Rotemberg, M. Palmeri, R. Nightingale, N. Rouze, and K. Nightingale, "The impact of hepatic pressurization on liver shear wave speed estimates in constrained versus unconstrained conditions," Physics in Medicine and Biology, 57, 329-341, January 2012.         [ Links ]

[21]. S. Chen, M. Fatemi, and J. F. Greenleaf, "Quantifying elasticity and viscosity from measurement of shear wave speed dispersion," The Journal of the Acoustical Society of America, 115, 2781, 2004.         [ Links ]

[22]. H. Hasegawa and H. Kanai, "Improving accuracy in estimation of artery-wall displacement by referring to center frequency of RF echo," IEEE Transactions on Ultrasonics Ferroelectrics and Frequency Control, 53, 52-63, 2006.         [ Links ]

[23]. A. H. Henni, C. Schmitt, and G. Cloutier, "Shear wave induced resonance elastography of soft heterogeneous media," Journal of Biomechanics, 43, 1488-1493, May 2010.         [ Links ]

[24]. G. Montaldo, M. Tanter, J. Bercoff, N. Benech, and M. Fink, "Coherent Plane-Wave Compounding for Very High Frame Rate Ultrasonography and Transient Elastography," IEEE Transactions on Ultrasonics Ferroelectrics and Frequency Control, 56, 489-506, March 2009.         [ Links ]

[25]. C. Kasai, K. Namekawa, A. Koyano, and R. Omoto, "Real-Time Two-Dimensional Blood Flow Imaging Using an Autocorrelation Technique," Sonics and Ultrasonics, IEEE Transactions on, 32, 458-464, 1985.         [ Links ]

[26]. M. Bernal, I. Nenadic, M. W. Urban, and J. F. Greenleaf, "Material property estimation for tubes and arteries using ultrasound radiation force and analysis of propagating modes," Journal of the Acoustical Society of America, 129, 1344-1354, March 2011.         [ Links ]

[27]. D. Alleyne and P. Cawley, "A two-dimensional Fourier transform method for the measurement of propagating multimode signals," The Journal of the Acoustical Society of America, 89, 1159-1168, 1991.         [ Links ]

[28]. N. Rognant, O. Rouviere, M. Janier, H. L. Quoc, P. Barthez, M. Laville, and L. Juillard, "Hemodynamic Responses to Acute and Gradual Renal Artery Stenosis in Pigs," American Journal of Hypertension. 23, 1216-1219, November 2010.         [ Links ]

[29]. T. J. Schmeling, D. A. Hettrick, J. R. Kersten, P. S. Pagel, and D. C. Warltier, "Changes in passive but not active mechanical properties predict recovery of function of stunned myocardium," Annals of Biomedical Engineering, 27, 131-140, March-April 1999.         [ Links ]

[30]. M. W. Urban, S. G. Chen, and J. F. Greenleaf, "Error in Estimates of Tissue Material Properties from Shear Wave Dispersion Ultrasound Vibrometry," IEEE Transactions on Ultrasonics Ferroelectrics and Frequency Control, 56, 748-758, April 2009.         [ Links ]