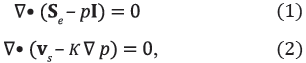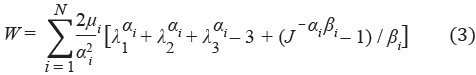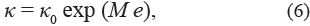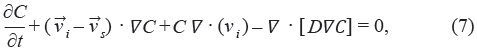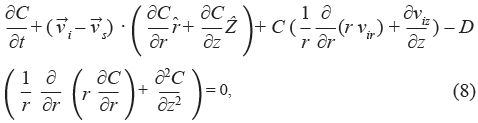Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares en
SciELO
Similares en
SciELO -
 Similares en Google
Similares en Google
Compartir
Revista Ingeniería Biomédica
versión impresa ISSN 1909-9762
Rev. ing. biomed. vol.8 no.16 Medellín jul./dic. 2014
PARAMETRIC ANALYSIS OF DRUG DISTRIBUTION DURING INFUSIONS INTO THE BRAIN USING AN AXISYMMETRIC MODEL WITH BACKFLOW
ANÁLISIS PARAMÉTRICO DE LA DISTRIBUCIÓN DE DROGA DURANTE INFUSIONES EN EL CEREBRO CON UN MODELO AXISIMÉTRICO CON REFLUJO
A ANÁLISE PARAMÉTRICA DE DISTRIBUIÇÃO DE DROGAS NO CÉREBRO DURANTE INFUSÕES COM UM MODELO AXISYMMETRIC COM REFLUXO
Gustavo A. Orozco1, Joshua H. Smith2, José J. García3
1 Escuela de Ingeniería Mecánica, Universidad del Valle. Cali, Colombia.
2 Department of Mechanical Engineering, Lafayette College. Easton, Pennsylvania, United States.
3 Escuela de Ingeniería Civil y Geomática, Universidad del Valle. Cali, Colombia. Dirección para correspondencia: josejgar@gmail.com.
Recibido 11 de agosto de 2014. Aprobado 1 de diciembre de 2014.
ABSTRACT
Convection-enhanced delivery as a means to deliver therapeutic drugs directly to the brain has shown limited clinical efficacy, primarily attributed to the phenomena of backflow, in which the infused fluid flows preferentially along the shaft catheter rather than forward into the tissue. We have previously developed a finite element model of backflow that includes both material and geometric nonlinearities and the free boundary conditions associated with the displacement of the tissue away from the external surface of the catheter. However, that study was limited to predictions of the tissue deformation and resulting convective fluid velocity in the interstitial space. In this study, we use results from that model to solve for the distribution of the infused therapeutic agent. We demonstrate that a significant percentage of the infused drug is not transported into the region of tissue located forward from the catheter tip, but instead is transported into the region along the lateral sides of the catheter. For lower flow rates, this study suggests that the use of a catheter with a larger radius may be preferable since it will provide the higher amount of drug to be transported to the tissue in front of the catheter. In contrast, for higher flow rates consistent with clinical infusions, the radius of the infusion catheter had minimal effect on the distribution of the infused drug, with most being transported into the tissue around the shaft of the catheter.
KEYWORDS: Convection-enhanced delivery, Infusion drugs, Computational model, Mass transport, Brain tumors.
RESUMEN
Convection-enhanced delivery es una técnica que permite transportar drogas directamente en el cerebro para el tratamiento de enfermedades del sistema nervioso central. Este método ha mostrado una eficacia limitada debido principalmente al fenómeno de reflujo (backflow), según el cual, el fluido inyectado fluye preferiblemente a lo largo del catéter y no hacia el tejido delante de la punta. Previamente desarrollamos un modelo de elementos finitos para representar el reflujo, el cual incluye las no linealidades geométricas y del material y las condiciones de borde libre asociadas con el desplazamiento del tejido en la superficie externa del catéter. Sin embargo, ese modelo solo predice la deformación del tejido y el campo de velocidades en el espacio intersticial. En este estudio, hemos utilizado los resultados provenientes del mencionado modelo bifásico para resolver la ecuación de transporte de masa y predecir la distribución de droga suministrada. Se pudo demostrar que un porcentaje significativo de droga no penetra en el tejido ubicado delante de la punta del catéter, sino que es transportado hacia el tejido ubicado alrededor del catéter. Para bajo caudales, este estudio sugiere que el uso de un catéter con un radio mayor permitiría transportar una mayor cantidad de droga hacia el tejido al frente de la punta. Por otro lado, para los mayores caudales usados en la práctica clínica, el radio del catéter tiene un efecto marginal en la distribución del fármaco, y la mayor cantidad de droga se transporta hacia el tejido ubicado alrededor del catéter.
PALABRAS CLAVE: Entrega mejorada por convección, Infusión de drogas, Modelo computacional, Transporte de masa, Tumores Cerebrales.
SUMÁRIO
Convection-enhanced delivery é uma técnica para o transporte de drogas directamente no cérebro para tratar doenças do sistema nervoso central. Este método tem demonstrado eficácia limitada devido, principalmente, ao fenómeno de refluxo (refluxo), através do qual, de preferência, o fluido injectado flui através do cateter para o tecido e não à frente da ponta. Anteriormente desenvolvido um modelo de elementos finitos para representar a refluxo, que inclui geométricas e não-linearidades do material e as condições associadas com a extremidade livre de deslocamento da trama na superfície exterior do cateter. No entanto, este modelo apenas prevê deformação do tecido e campo de velocidades no espaço intersticial. Neste estudo, foram utilizados os resultados do modelo de duas fases acima referidas, para resolver a equação de transporte e prever a distribuição de massa de medicamentos fornecidos. Demonstrou-se que uma percentagem significativa da droga não penetra no tecido localizado em frente da ponta do cateter, que é transportado para o tecido que rodeia o cateter. Para as taxas de fluxo baixas, este estudo sugere que o uso de um cateter com um raio maior do que transportar uma maior quantidade de droga para o tecido em frente da ponta. Além disso, para taxas de fluxo mais elevadas utilizadas na prática clínica, o raio do cateter tem um efeito marginal sobre a distribuição da droga, e tanto fármaco é transportado para o tecido que rodeia o cateter.
PALAVRAS-CHAVE: Convecção reforçada entrega, a infusão de drogas, modelo computacional, transporte de massa, tumores cerebrais.
I. INTRODUCCIÓN
Convection-enhanced delivery (CED) is a method that was developed to treat cerebral diseases by infusing therapeutic agents directly into the brain under positive pressure in order to avoid the blood-brain barrier. Whereas controlled animal studies have been encouraging [1-3], clinical trials [4] have shown limited efficacy of this technique, attributed to poor distribution of the drug into the targeted region, which may be due to backflow, in which the infused fluid flows toward the surface of the brain along the annular gap formed outside the surface of the catheter. Hence, a significant amount of drug may be transported into the tissue from the lateral surface formed around the catheter rather than from the infusion cavity formed around the catheter tip.
In order to understand the physics of the problem and to improve the infusion protocols, several theoretical models have been developed to calculate drug distribution during infusions into the brain. Generally these models assume that brain tissue is rigid or behaves as a linear elastic material under infinitesimal deformations [5-7]. However, given the compliant nature of brain tissue, substantial deformations are generated during infusions, as it has been documented in animal studies [8]. In addition, experimental testing has shown that brain tissue exhibits nonlinear stress-strain curves under finite deformations [9, 10]. As shown in the study by Smith and García [11], which includes geometrical and material nonlinearities, the consideration of the finite deformations of the tissue around the infusion cavity greatly modifies the contours of drug distribution with respect to those predicted for rigid materials. However, the model described by Smith and García [11] was based in a simplified spherical model that does not include backflow.
A recent finite element model that includes backflow and considers material and geometrical nonlinearities was developed to predict fluid flow under flow-controlled infusions [12]. Nonetheless, this model does not solve the mass transport equation in order to predict the distribution of the infused drug. Hence, the objective of this study was to solve the mass transport equation to calculate drug distributions under flow-controlled infusions, considering the backflow zone and the nonlinear effects included in our previous model of fluid transport [12]. The model was used to perform a parametric analysis in order to determine the sensitivity of results under variations of flow rate, catheter radius, tissue shear modulus and hydraulic conductivity, and effective drug diffusivity.
II. METHODS
To consider the deformation of the tissue that has shown to be substantial during infusions into animal brain tissue [8], the solution of the mass transport equation required information about the deformations and the interstitial fluid velocity that occurs during infusion. Predictions for these were obtained using our previously developed biphasic model [12], which is briefly explained below, for the sake of completeness.
2.1 Biphasic Finite Element Model of Infusion
The model of infusion represents brain tissue as a biphasic medium consisting of solid and fluid phases. This theory assumes that both phases are intrinsically incompressible but that the medium may compress by expulsion of the fluid. The governing equations are force equilibrium and mass conservation of the mixture [12], which may be respectively expressed as
where Se is effective Cauchy stress tensor, p is the interstitial fluid pressure, I is the identity tensor, vs is the velocity of the solid matrix, and κ is the hydraulic conductivity.
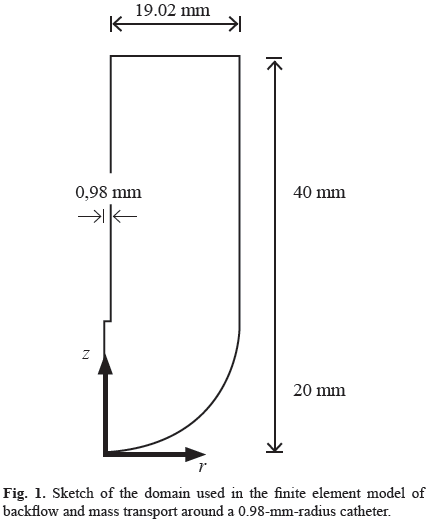
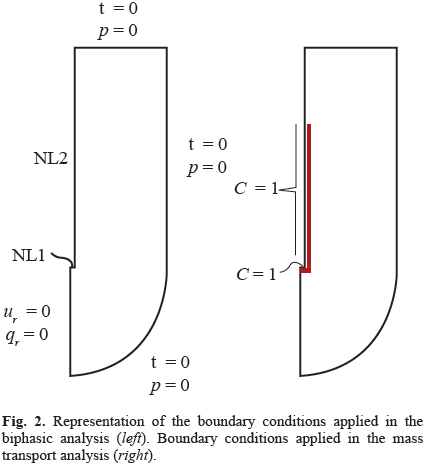
The model includes geometric and material nonlinearities, strain-dependent hydraulic conductivity, and the consideration of the free boundary problems that occur at the catheter tip and around the outer surface of the catheter resulting from backflow along the catheter shaft [13]. It was developed using ABAQUS 6.10 (Simulia, Providence, RI) considering axial symmetry and the planar geometry of Fig. 1, and it was calibrated with published experimental data [14]. The free boundary problems were treated using two specially formulated layers at the tip and side of the catheter (Fig. 2a), as explained in detail in references [12].
The infused material was represented as a biphasic medium composed of solid and fluid phases. The solid phase was represented with the following Ogden-type compressible hyperelastic energy function
where λ1, λ2, λ1 are the principal stretch ratios, αi, µi, and βi are material parameters, and J is the determinant of the deformation gradient tensor. The coefficients are related to the initial shear modulus G by
and the parameters βi are related to the Poisson's ratio ν by
The nonlinear parameter αi was taken to be -4.71, consistent with the experimental studies on brain tissue of Miller and Chinzei [10], and the Poisson's ratio was taken to be 0.35, in agreement with other analyses [6, 7, 11, 12]. Also, the hydraulic conductivity was assumed to depend on tissue dilatation as
where κ0 is the hydraulic conductivity at zero strain, M is a non-dimensional parameter, and e is the volumetric dilation.
2.2 Infusion Mass Transport Model with Backflow
Fluid and solid velocities, fluid fractions, and displacements from the biphasic model were used for the solution of the mass transport equation. The appropriate form of the convective-diffusive mass transport equation [6, 11] is
where C is the concentration of the chemical species per unit volume of tissue, 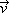 i is the interstitial fluid velocity vector, and D is the effective diffusion coefficient. It was assumed that transport is limited to the interstitial space and that no vascular or cellular absorption occurs.
i is the interstitial fluid velocity vector, and D is the effective diffusion coefficient. It was assumed that transport is limited to the interstitial space and that no vascular or cellular absorption occurs.
We assumed an axial symmetry consistent with other models [12] and experimental tests [13, 14]. This geometry consists of a cylinder extending between the radius of the catheter and an outer surface of 20-mm radius with a hemisphere of that radius at the catheter tip (Fig. 1). For an axial symmetric geometry, the (7) may be represented by the following equation:
where r and z are the current radial and axial coordinates, respectively; and 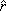 and
and 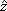 are unit vectors along the radial and axial directions. In addition, vir and viz are the radial and axial components of the interstitial fluid velocity vector, respectively.
are unit vectors along the radial and axial directions. In addition, vir and viz are the radial and axial components of the interstitial fluid velocity vector, respectively.
Eq. (8) was solved numerically using the finite element method in space with the Galerkin approach for the interpolating functions while the time derivative was approximated with the Euler's backward difference. A custom-written axisymmetric program was developed in MATLAB (Mathworks, Natick, MA), which efficiently imported the output files from the biphasic model and solved the mass-transport equation. Based on a convergence study, meshes of 3680, 3431, 3364, and 3241 axisymmetric elements of type CAX4P were used for a catheter radius of 0.150, 0.33, 0.50, and 0.98 mm, respectively.
With respect to the boundary conditions for the mass transport infusion model, the drug concentration on the infusion surface was assumed to be equal to the infused agent and it was normalized to one. On the external side of the catheter, the drug concentration is initially unknown. As infusion proceeds and due to backflow, the tissue near the catheter tip separates from the outer surface of the catheter and the boundary condition changes to be a known drug concentration. As a first approximation, drug concentration along the backflow length on the surface of the catheter was assumed to be equal to the normalized fluid concentration (Fig. 2b).
2.3 Model Verification
We made several comparisons in order to verify our code. First, for a rigid domain, numerical concentrations were compared with closed-form solutions that can be obtained by independently considering axial and radial flow, for both steady and transient states. Second, considering that there are no analytical solutions including the various sources of nonlinearities associated with the problem, our code was verified using a previously developed finite element program based on spherical geometry, which includes finite deformations, material nonlinearities, and the variation of hydraulic conductivity with strain [11]. Those simulations were performed using similar baseline parameters published in that study. Finally, using a more general geometry (Fig. 1) and all sources of nonlinearities, a mass balance convergence was conducted for the case of a small diffusion coefficient so that drug mass transport into the tissue was dominated by convection.
2.4 Parametric Analysis
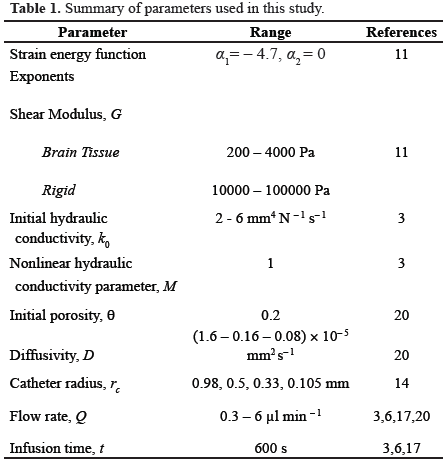
We performed an analysis in order to determine the sensitivity of our results to variations in the infusion parameters. First, we considered two materials, one with elastic properties similar to those of brain tissue and another with stiffer properties, in order to obtain results that could be compared with those of other models that adopted the hypothesis of infinitesimal deformations. We performed 272 simulations for the brain-like material and 162 simulations for the rigid material under variations of infusion parameters within the ranges shown in Table 1, which reproduce conditions adopted in experimental or clinical infusions [1, 4, 15] or are consistent with previous theoretical studies [11, 16, 17]. The total infusion time was set 600 seconds, consistent with other numerical studies [6, 11, 18, 19]. To more exactly describe the drug distributions, we defined four regions (Fig. 3): tip gap, annular gap, forward tissue, and lateral tissue. The first two, tip gap and annular gap, described the infusion cavity and the backflow zone around the catheter, respectively, and are both filled with fluid. The other two, forward tissue and lateral tissue, described the regions of the tissue in front of the catheter tip and around the outer cylinder of the catheter, respectively.
III. RESULTS
3.1 Model Verification
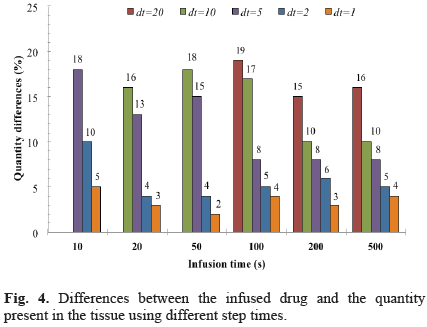
The predicted numerical concentrations yielded differences less than 2% with respect to the closedform solutions. The verification with a spherical symmetrical finite element code [11] showed differences of concentration lower than 5% for a wide range of material properties that were included in the comparison [20]. For the mass balance verifi cations including all nonlinear effects and the domain with the backflow zone (Fig. 1), it was observed that a decrease in the time step resulted in a decreased error between the infused drug and the quantity present in the tissue. For example, differences were less than 5% using a time step of 1 s (Fig. 4). There were no spatial instabilities for the values of the diffusion coefficient D considered in this analysis since pilot simulations showed these instabilities arose for diffusivities less than 8.0×10-6 mm2 s-1 for the stiffer materials and less than 5.0×10-6 mm2 s-1 for the softer materials. For each case, the Peclet number was within the range 500-1000, which means that the transport phenomenon was dominated by convection.
3.2 Drug Distributions from Parametric Analysis
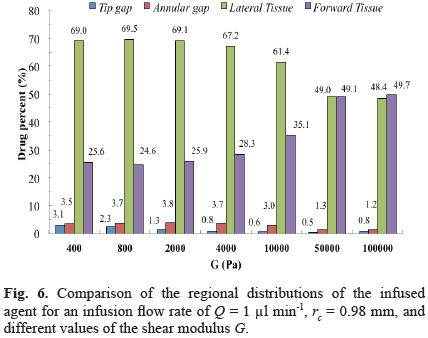
The effect of varying mechanical properties on final drug distribution was substantial when comparing rigidlike materials (shear modulus G > 50000 Pa) and brainlike materials (G < 4000 Pa). Generally, a shorter backflow length and a deeper drug penetration along both the radial and axial directions were obtained for the stiffer material (Fig. 5b). The drug was more uniformly distributed for the softer materials, whereas there was a peak at the corner of the catheter for the stiffer material, which appears to be due to an increase in the fluid velocity at this location (Fig. 5a). This peak did not appear for the softer material due to the larger deformation of the tissue. For a flow rate of 1 µl/min and values of G between 400 and 4000 Pa, the relative distribution in the four sections of the domain was rather similar, characterized by a drug content in the lateral tissue above 60%, which was between two and three-fold the drug content in the forward tissue (Fig. 6). This distribution tendency changed for more rigid materials, with the drug content almost equal in the lateral and forward sections for shear moduli higher than 50000 Pa (Fig. 6).
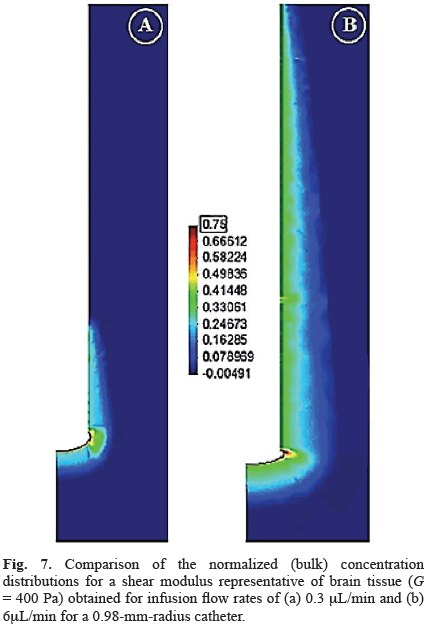
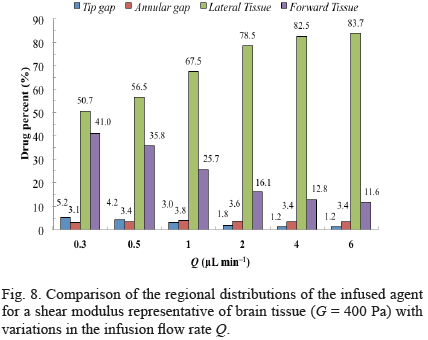
For both low and high flow rates, substantial deformations as well as maximum concentrations localized around the catheter tip were obtained for brain-like materials (Fig. 7). For all flow rates considered, models with a shear modulus similar to brain tissue had over 50 percent of the infused drug transported into the lateral region of the tissue (Fig. 8). For increments in flow rate, the drug distribution increased in the lateral region, decreased in the forward tissue and the tip gap, and was relatively constant in the annular gap (Fig. 8).
We next present results for variations of parameters with respect the following baseline values: catheter radius rc = 0.98 mm, shear modulus G = 2000 Pa, initial hydraulic conductivity κ0 = 2 mm4 N-1 s-1, nonlinear permeability parameter M = 1, and diffusion coefficient D = 1.6 10-5 mm2 s-1, as shown in Table 2. Two flow rates (0.3 µl/min and 6 µl/min) were considered in this comparison.
For a flow rate of 0.3 µl/min and reductions of the catheter radius, there was an increase of drug content in the lateral region as well as important decreases in the forward tissue, the tip gap and the annular gap, e.g., up to 43% reduction in the forward tissue and up to 25% increase in the lateral tissue for a catheter radius of 0.105 mm (Table 2). The same tendency was observed for the flow rate of 6 µl/min, however, the variations were not as high as those observed for the lower flow rate, e.g., up to 17% decrease in the forward tissue and up to 4% increase in the lateral tissue for rc = 0.105 mm.
Decreases in the shear modulus G yielded a rather constant drug content in the lateral tissue region (changes less than 2%) and accumulation of the drug in the tip gap, e.g., differences up to 128% and 92% for 0.3 µl/min and 6 µl/min, respectively (Table 2). However, whereas the drug content increased in the annular gap and decreased in the forward tissue for reductions of G and Q = 0.3 µl/min, it decreased in the annular gap and increased in the forward tissue for Q = 6 µl/min.
There were decreases in the content in the lateral region and increases in the forward tissue for increases of the initial hydraulic conductivity. However, for 6 µl/min, this decrease of content was rather low (-5%). Change of one order of magnitude in the diffusivity parameter D had a marginal effect on content distribution (Table 2).
IV. DISCUSSION
To the best of our knowledge, this is the first model to predict drug distribution during infusions into the brain that includes material and geometrical nonlinearities and the consideration of backflow. Results showed the important influence of including large deformations compared to analyses that consider the infused domain to be rigid. For instance, while the prediction of drug content in the tissue in front of the catheter tip for a rigid domain was about 50%, it was only around 25% for a domain with elastic properties similar to those of brain tissue.
The difference of drug content distributions between rigid-like and brain-like materials may be primarily attributed to the larger backflow length predicted for softer materials that greatly enhances the drug distribution toward the lateral section of the tissue, which may be many times larger than the infusion cavity in front of the catheter tip. This explains why the simulations predict that a significant proportion of the drug is transported into the tissue surrounding the catheter rather than forward of the tip. The higher penetration of the drug for rigid-like materials (Fig. 5) may be explained by the smaller expansion of the interstitial spaces compared to the substantial increases in void fraction that have been documented for brain-like materials in other computational models [11, 21], and in the experimental studies [5, 22]. Additionally, the relevance of the increasing of void fraction on brain tissue has been highlighted in a specific algorithm [23] to provide better drug coverage around the catheter tip. A higher penetration implies that a higher volume of infusion will be predicted with a rigid model, which is consistent with the results presented by Kim et al. [24] showing that the predictions of the infusion volume from their rigid model are about 20% greater than the experimental measurements in rats. The rigid models [24, 25] are also unable to predict drug accumulation due to the increase in porosity around the catheter tip, as has been documented in other studies [5, 11].
Simulations also showed that the drug content in the lateral tissue was relatively constant for brain-like materials and higher flow rates under variations of parameters like catheter radius and shear modulus (Table 2). This is consistent with results of computational simulations showing that the influence of the catheter radius and shear modulus on backflow length is marginal when nonlinear effects such as finite deformations generated under higher flow rates are included in the analyses [20]. Under these conditions, the higher percent of the drug is transported from the backflow surface, which is relatively large compared to the area of the infusion cavity.
Decreases of drug content in the tip gap and annular gap for decreases of catheter radius are explained by the lower volume of these gaps, which grossly decreases with the cube of the catheter radius. In addition, under lower flow rates (0.3 µl/min), a higher proportion of the backflow zone is near to the catheter tip and the area of the infusion surface is comparable to that of the annular volume around the backflow zone (Fig. 7). Hence, this implies that a higher proportion of the drug is transported from the catheter tip and makes the influence of variations, such as the catheter radius, more marked in the relative distribution of the drug.
On the other hand, higher drug contents in the lateral tissue under higher flow rates may be explained by the longer backflow lengths and deformations caused by the augmented dragging action of the fluid flow over the poroelastic tissue, which is consistent with the results presented by Casanova et al [26]. Drug content predictions were not sensitive to diffusivity changes since the transport phenomenon analyzed in this study was dominated by convection, as characterized by large Peclet numbers. Similar conclusions were obtained in another study [11] under a spherical geometry that considers similar parameters and the nonlinearities of the problem.
No spatial instabilities were present for the ranges of shear modulus and diffusivity used in this study using the traditional Galerkin method even though the Peclet number was as high as 1000 for the softer material. From the clinical point-of view, results of the study showing increases of drug content in the lateral tissue for smaller catheters, more markedly for lower flow rates, suggests that the use of a catheter with a larger radius may be preferable since it will provide a higher amount of drug to be transported to the tissue in front of the catheter. In addition, under flow-controlled infusions, the pressure is lower for larger catheter radius. Hence, a lower degree of tissue damage may be expected for a larger catheter radius due to the lower values of stress associated with the infusion pressure.
This study was performed using an axisymmetrical geometry and assuming a homogeneous material. Our next endeavor will be the implementation of the model in realistic 3-D geometries in order to be able to quantify the influence on drug distribution of anatomical details, such as the ventricles. Another limitation is that the anisotropy of the hydraulic conductivity was not taken into account in the initial non-deformed configuration. However, the variation of strain with the hydraulic conductivity was included in the model, which allows to describe changes in highly expandable sections, which has been suggested to be the main mechanism behind the preferential flow observed in white tissue matter [27, 28]. It has to be noted that the significant effects of finite deformations analyzed in this study will also constitute a main component of future models.
CONFLICTS OF INTEREST
There are no conflicts of interest.
ACKNOWLEDGMENTS
The authors appreciate the support of the Universidad del Valle and Lafayette College to undertake this study. Thanks are also due to Colciencias program 516-2012 (contract #110656933826) "Programa Nacional de Ciencia y Tecnología de la Salud" for the financial support.
REFERENCES
[1]. Krauze M. T., Mcknight T. R., Yamashita Y., Bringas J., Noble C. O., Saito R., Geletneky K., Forsayeth J., Berger M. S., Jackson P., Park J. W., and Bankiewicz K. S. Real-time visualization and characterization of liposomal delivery into the monkey brain by magnetic resonance imaging. Brain Res. Protoc., 16, 20-26, December 2005. [ Links ]
[2]. Krauze M. T., Forsayeth J., Park J. W., and Bankiewicz K. S. Realtime imaging and quantification of brain delivery of liposomes, Pharm. Res., 23, 2493-2504, November 2006. [ Links ]
[3]. Rosenbluth K. H., Martin A. J., Bringas J., and Bankiewicz K. S. Evaluation of pressure-driven brain infusions in nonhuman primates by intra-operative 7 Tesla MRI. J. Magn. Reson. Imaging, 36, 1339-1346, June 2012. [ Links ]
[4]. Sampson J. H., Archer G., Pedain C., Wembacher-Schröder E., Westphal M., Kunwar S., Vogelbaum M. A., Coan A., Herndon J. E., Raghavan R., Brady M. L., Reardon D. A., Friedman A. H., Friedman H. S., Rodríguez-Ponce M. I., Chang S. M., Mittermeyer S., Croteau D., and Puri R. K. Poor drug distribution as a possible explanation for the results of the PRECISE trial. J. Neurosurg., 113, 301-309, August 2010. [ Links ]
[5]. Brady M., Raghavan R., Chen Z.-J., and Broaddus W. C. Quantifying fluid infusions and tissue expansion in brain. IEEE Trans. Biomed. Eng., 58, 2228-2237, August 2011. [ Links ]
[6]. Chen X. and Sarntinoranont M. Biphasic finite element model of solute transport for direct infusion into nervous tissue. Ann. Biomed. Eng., 35, 2145-2158, December 2007. [ Links ]
[7]. Stoverud K. H., Darcis M., Helmig R., and Hassanizadeh S. M. Modeling concentration distribution and deformation during convection-enhanced drug delivery into brain tissue. Transp. Porous Media, 92, 119-143, March 2012. [ Links ]
[8]. Valles F., Fiandaca M. S., Bringas J., Dickinson P., LeCouteur R., Higgins R., Berger M., Forsayeth J., and Bankiewicz K. S. Anatomical compression due to high volume convection-enhanced delivery to the brain. Neurosurgery, 65, 579-586, September 2009. [ Links ]
[9]. Franceschini G., Bigoni D., Regitnig P., and Holzapfel G. A., Brain tissue deforms similarly to filled elastomers and follows consolidation theory. J. Mech. Phys. Solids, 54, 2592-2620, December 2006. [ Links ]
[10]. Miller K. and Chinzei K. Mechanical properties of brain tissue in tension. J. Biomech., 35, 483-490, April 2002. [ Links ]
[11]. Smith J. H. and García J. Jaime. A nonlinear biphasic model of flow-controlled infusions in brain: Mass transport analyses. J. Biomech, 44, 524-531, February 2011. [ Links ]
[12]. García J. J., Molano A. B., and Smith J. H. Description and validation of a finite element model of backflow during infusion into a brain tissue phantom. J. Comput. Nonlinear Dyn, 8, 011017, January 2013. [ Links ]
[13]. Morrison P. F., Chen M. Y., Chadwick R. S., Lonser R. R., and Oldfield E. H. Focal delivery during direct infusion to brain: Role of flow rate, catheter diameter, and tissue mechanics. Am. J. Physiol, 277, R1218-R1229, January 1999. [ Links ]
[14]. Raghavan R., Mikaelian S., Brady M., and Chen Z.-J. Fluid infusions from catheters into elastic tissue: I. Azimuthally symmetric backflow in homogeneous media. Phys. Med. Biol., 55, 281-304, January 2010. [ Links ]
[15]. Brady M. L., Raghavan R., Alexander A., Kubota K., Sillay K., and Emborg M. E. Pathways of infusate loss during convectionenhanced delivery into the putamen nucleus, Stereotact. Funct. Neurosurg., 91, 69-78, January 2013. [ Links ]
[16]. García J. J. and Smith J. H. A biphasic hyperelastic model for the analysis of fluid and mass transport in brain tissue. Ann. Biomed. Eng., 37, 375-386, February 2009. [ Links ]
[17]. Smith J. H. and García J. J. A nonlinear biphasic model of flowcontrolled infusion in brain: Fluid transport and tissue deformation analyses. J. Biomech., 42, 13, 2017-2025, September 2009. [ Links ]
[18]. Sarntinoranont M., Banerjee R. K., Lonser R. R., and Morrison P. F. A computational model of direct interstitial infusion of macromolecules into the spinal cord. Ann. Biomed. Eng., 31, 448-461, April 2003. [ Links ]
[19]. Sarntinoranont M., Chen X., Zhao J., and Mareci T. H. Computational model of interstitial transport in the spinal cord using diffusion tensor imaging. Ann. Biomed. Eng., 34, 1304-1321, August 2006. [ Links ]
[20]. Orozco A., Smith J. H., and García J. J. Predictions of drug distribution during infusions into the brain using an axisymmetric finite element biphasic model that includes backflow. Proceedings of the 2013 ASME Sum. Bio. Conf., Oregon, USA, June, 2013. [ Links ]
[21]. Raghavan R. and Brady M. Predictive models for pressure-driven fluid infusions into brain parenchyma. Phys. Med. Biol., 56, 6179-6204, October 2011. [ Links ]
[22]. Sampson J. H., Raghavan R., Provenzale J. M., Croteau D., Reardon D. A., Coleman R. E., Ponce I. R., Pastan I., Puri R. K., and Pedain C. Induction of hyperintense signal on T2-weighted MR images correlates with infusion distribution from intracerebral convection-enhanced delivery of a tumor-targeted cytotoxin. Amer. J. Roentgenology, 188, 703-709, November 2007. [ Links ]
[23]. Sampson J. H., Raghavan R., Brady M. L., Provenzale J. M., Herndon J. E., Croteau D., Friedman A. H., Reardon D. A., Coleman R. E., Wong T., Bigner D. D., Pastan I., Rodríguez-Ponce M. I., Tanner P., Puri R., and Pedain C. Clinical utility of a patientspecific algorithm for simulating intracerebral drug infusions. Neuro-Oncol., 9, 343-353, January 2007. [ Links ]
[24]. Kim J. H., Mareci T. H., and Sarntinoranont M. A voxelized model of direct infusion into the corpus callosum and hippocampus of the rat brain: model development and parameter analysis. Med. Biol. Eng. Comput., 48, 203-214, March 2010. [ Links ]
[25]. Kim J. H., Astary G. W., Kantorovich S., Mareci T. H., Carney P. R., and Sarntinoranont M. Voxelized computational model for convection-enhanced delivery in the rat ventral hippocampus: comparison with in vivo MR experimental studies. Ann. Biomed. Eng., 40, 2043-2058, September 2012. [ Links ]
[26]. Casanova F., Carney P. R., and Sarntinoranont M. Effect of needle insertion speed on tissue injury, stress, and backflow distribution for convection-enhanced delivery in the rat brain. PLoS ONE, 9, e94919, April 2014. [ Links ]
[27]. White E., Bienemann A., Malone J., Megraw L., Bunnun C., Wyatt M., and Gill S., An evaluation of the relationships between catheter design and tissue mechanics in achieving high-flow convectionenhanced delivery. J. Neurosci. Methods, 199, 87-97, July 2011. [ Links ]
[28]. Yin D., Valles F. E., Fiandaca M. S., Bringas J., Gimenez F., Berger M. S., Forsayeth J., and Bankiewicz K. S. Optimal region of the putamen for image-guided convection-enhanced delivery of therapeutics in human and non-human primates, NeuroImage, 54, S196-S203, January 2011. [ Links ]