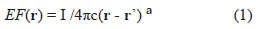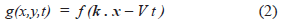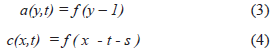Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares en
SciELO
Similares en
SciELO -
 Similares en Google
Similares en Google
Compartir
Revista Ingeniería Biomédica
versión impresa ISSN 1909-9762
Rev. ing. biomed. vol.9 no.17 Medellín ene./jun. 2015
FIELD GENERATED BY WAVES, SEQUENTIAL ACTIVATIONS AND APPARENT MOTION: EFFECTS AND TYPICAL PATTERNS
CAMPOS GENERADOS POR ONDAS, ACTIVACIONES SECUENCIALES Y MOVIMIENTO APARENTE: EFECTOS Y PATRONES TÍPICOS
CAMPOS ONDAS GERADAS, ATIVAÇÕES SEQÜENCIAIS E MOVIMENTO APARENTE: EFEITOS E PADRÕES TÍPICOS
Juan Fernando Gómez-Molina1, Alberto Antonio Restrepo Velázquez2, Luis Fernando Botero Posada3
1 International Group of Neuroscience. Medellín, Colombia. Dirección para correspondencia: gomezmoljfmedcol@gmail.com.
2 Informática y Sistemas. EAFIT University, Medellín, Colombia.
3 Medicine Department, Universidad CES, Medellin, Colombia.
ABSTRACT
Important components of the Extracellular Field (EF) can be caused by a sequential or moving depolarization generated by some cell-groups at specific sub-regions. These depolarizations can be sensed not only by man-made techniques -as electroencephalography (EEG) and electrocardiography (ECG) - but also by some physiological processes associated to ephaptic interactions. METHODS: Based on principles of electromagnetism we implement two computer simulations where this can be studied: 1. Bilateral waves, where subregions can have up to 3 mesoscopic states: activated, resting or sleeping (hyperpolarized) and 2. Stochastic propagation without deactivation. RESULTS: Biphasic, Gaussian and Mexican hat functions can be generated by these models. CONCLUSIONS: (i) Mesoscopic minimalistic models can explain in a simple way some electrophysiological signals. (ii) We suggest an analogy between mechanisms used in animal and robots to detect visual motion and engineering techniques to detect moving depolarizations in the nervous system. Similarly, such mechanisms might exist in cell-groups. (iii) Distorted waves can cause pathologies and their modulation by electric or magnetic stimulation can be potentially beneficial.
KEYWORDS: Electrophysiology, Models, Motion detection, Waves, Local and global states.
RESUMEN
Componentes importantes de los campos extracelulares (CE) pueden ser causados por despolarización secuencial o en movimiento, generadas por algunos grupos celulares en subregiones específicas. Estas despolarizaciones pueden ser detectadas no solo con técnicas hechas por el hombre -como la electroencefalografía (EEG) o la electrocardiografía (ECG)- sino también por algunos procesos fisiológicos asociados con interacciones por efectos directos de campo eléctrico local. MÉTODOS: Basados en principios del electromagnetismo nosotros implementamos dos simulaciones de computador donde esto puede ser estudiado: 1. Ondas bilaterales, donde las subregiones pueden tener hasta 3 estados mesoscópicos: activación, reposo o dormido (hiperpolarización) y 2. Propagación estocástica sin desactivación. RESULTADOS: Funciones bifásicas, Gaussianas y tipo sombrero mexicano pueden ser generadas por estos modelos. CONCLUSIONES: (i) Modelos mesoscópicos minimalísticos pueden explicar de una manera simple algunas señales electrofisiológicas. (ii) Sugerimos una analogía entre mecanismos usados en animales y robots para detectar movimiento visual y técnicas de ingeniería para detectar despolarizaciones en movimiento en el sistema nervioso. Asimismo, tales mecanismos pueden existir en grupos celulares. (iii) Ondas distorsionadas pueden causar patologías y su modulación con estimulación eléctrica y magnética puede ser beneficiosa.
PALABRAS CLAVE: Detección de movimiento, Electrofisiología, Modelos, Ondas, Estados locales y globales.
RESUMO
Os principais componentes do campos extracelulares ( CE ) pode ser causada por movimentos despolarizações seqüenciais ou alguma célula adj Gerado em grupos sub-regiões específicas . Está despolarizações pode ser detectado não apenas as técnicas feita pelo homem , tais como a eletroencefalografia (EEG) e eletrocardiograma (ECG) - Sino também para algumas adj associados processos fisiológicos com interações epapticas . MÉTODOS : Com base em : princípios do eletromagnetismo Implementamos duas simulações de computador onde este pode ser estudada : 1. ondas bilaterais , onde as sub-regiões podem ter até 3 ESTADOS mesoscópicos : ativação, descanso ou hiperpolarização e 2. estocástico propagação pecado desativação. RESULTADOS: funções bifásicos , Gaussian e tipo chapéu mexicano pode ser gerada por esses modelos. CONCLUSÕES : (i) minimalisticos modelos mesoscópicos pode explicar de uma forma simples Alguns sinais eletrofisiológicos . (Ii) sugerir uma analogia entre -mecanismos de animais e robôs usados para detectar movimento visual e técnicas afins despolarizações Pará detectar movimento no sistema nervoso . Além disso, histórias de mecanismos podem existir em grupos de células . (Iii) as doenças podem causar ondas distorcidas e modulação estímulo elétrico e magnético pode ser benéfico.
PALAVRAS-CHAVE: Detecção de movimento, Eletrofisiologia, Models, Waves, Estados locais e globais.
I. INTRODUCTION
In clinical electrophysiology there are many cases of waves, sequential activations, and apparent "electric motion": for instance, the activation of neural pathways by a sensory stimulus during evoked responses [1]; the propagation of hyper-synchronous activity in epilepsy [2]; the moving depolarizations in the heart [3]; and the traveling of the slow wave oscillation during sleep [4].
It is then reasonable to model the sources of a diverse variety of electrophysiological signals as electrical activities that "move" following some trajectories. The biological source models that have been used for this purpose include: monopoles, dipoles, or specific ionic currents [3]. On the other hand, when a source is going to generate an EF, the first and more fundamental event is the opening and/or closing of ionic channels [3-7]. Big complexes of ion channels (cells, columns) inherit the 3 states of the channels [8]: activation (functional or open); resting (closed or easy to activate) and "asleep" (hyperpolarized; hard or unlikely to be active). Algorhythms that apply to both, local and global states, help to simplify computer programs.
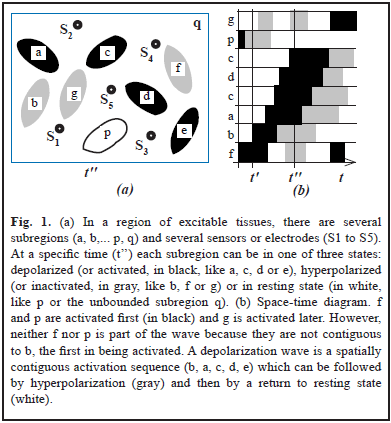
However, the relation between the EF recordings and the state of the sources is not simple. Depending on the model used, such relation might depend on: (a) The magnitude, polarity and orientation of the source; (b) The position and distance between sources and sensors. (c) The geometric and conductive properties of the medium as well as its degree of isotropy and homogeneity [3]. Moreover, some waves might not be waves in the classical sense [9]. Let's consider for instance a region composed of several subregions (Fig. 1a). Methods to check for wave structure [10] use space-time diagrams (Fig. 1b) which display time along the horizontal axis and spatial subregions or positions along the vertical axis. Subregions can be ordered by onset of activation.
On the other hand, EF has been considered a byproduct of the brain with few physiological effects, but this view has been changing [11]. In this context, the space-time EF-pattern generated by waves can tell us where (beyond, between or in front) ephaptic effects add constructively.
In this paper we use space-time diagrams to describe simulated waves. We chose two classes: bilateral waves (where strong contributions of left and right regions might produce stronger field effects) and "probability waves" where the probability of activation around the wave front might change by endogenous or exogenous EFs.
Finally, we suggest that the second ones might help the first to reverse or reform abnormal waves of some diseases.
II. MATERIALS AND METHODS
In order to simplify the Maxwell's equations of electromagnetism it is assumed that the medium has a purely homogeneous and isotropic conductivity. In this case the extracellular field EF is governed by Laplace's equation [3, 6]. For a single point source in an unbounded isotropic conductor the Laplace's equation can be simplified [3, 6]:
Where I is the current of the source; c depends on properties of the medium (e.g., conductivity); (r-r') is the magnitude of the vector between the vector-distance of sensor, r, and source r'. a = 1; similar EF-waveform is expected for the multipolar case, a > 1. To focus on waves vs. general EF (EEG, ECG, MEG, MCG), we assume: (a) averages for other confounding factors and (b) discrete-states of activity [8] (I = 0 at resting state; I = 1 at activated state). Units of EF are in terms of I/c; units of t are arbitrary.
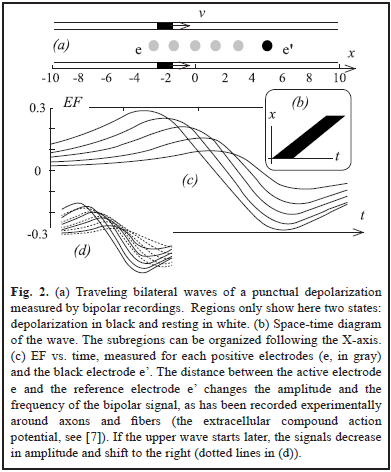
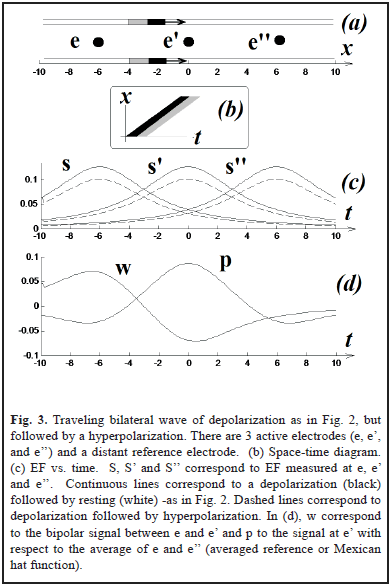
In two simulations (Fig. 2a and 3a), we have two punctual sources moving at constant velocity and describing two parallel lines. This simple scenario will allow us to easily translate our results from time to space, something that can be important to interpret the field effect in terms of neural coding. For Fig. 3a the magnitude of the hyperpolarization was 0.2.
The computer programs were coded using MATLAB.
III. RESULTS
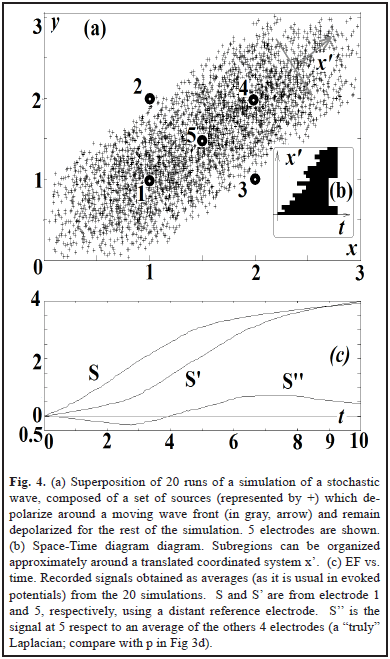
The results are shown in Fig. 2 and Fig. 3. Using a distant reference electrode and hyperpolarizations the magnitude of EF increases as the distance electrode-wave decreases and decreases with the presence of hyperpolarization (Fig. 3c). Subtracting EF of e and e' we obtain the signal w = S - S', which correspond to the same biphasic signal of Fig. 2c. Finally p = S - (S' + S'')/2 and it is equivalent to the computation of lateral inhibition in visual systems for detecting edges (subtraction between excitatory center e' vs. inhibitory periphery, e and e'') [5, 7, 12].
To analyze the effect on the EF of the profile of the wave, in Fig. 4 we generate a "stochastic wave": a directional but random propagation of persistent activation. This is a common feature of biological waves: slow oscillations in sleep originate more frequently in some places and propagate in some preferred directions [4] with a wavelength bigger than the spatial extension of the wave [9]. The profile of the waveform is variable and the onset of activation in the space-time diagram can only be approximated to a straight line (Fig. 4b). The sources remain activated (the equivalent to the movement of an edge of a big object in visual systems). The zero-crossing point of the laplacian (S'') is a way to indicate the crossing of the wavefront in electrode 5. A more clear way to detect this can be computing center vs. periphery. Delays can compensate for distances, as visual systems might do to detect motion [5, 7, 12, 13].
IV. DISCUSSION
It can be seen that any sequential activation of sources (from directional or expansive waves or even from random locations) produce a monotonically increasing EF in a sensor (with its reference electrode at distant location) as long as the sources do not hyperpolarize or return to resting state (deactivate). This is because all the depolarizations contribute positively to the active electrode, regardless of distance. For bipolar recordings, the relative distance between the center of the wave and each of the electrodes is relevant: if the center moves away of the positive ("excitatory") electrode and/or closer to the negative ("inhibitory") electrode, the EF is going to decay.
On the other hand, fast space-time patterns of EF can generate more effects on neurons than slower signals [14], in which potassium conductances can drive currents to resting states [5, 7]. It can be suggested that fast waves induce maximal ephaptic effects in the subregions that are going to be activated by the wave itself.
Can the model be generalized? Can it be approximated to more complex scenarios, closer to a clinical context?
The question can be answered qualitatively, if the waves are defined as special cases of the general form [15].
Where x = (x, y) and k = (k, k') is a unit vector specifying the wave direction [10]. The source is g(x, y, t). The profile shape of the wave is defined by f. V is the velocity of the wave and t is time.
Fig 5 (a) shows a simple case where g(x, t) = f(x - Vt), with V = L/t*. The shape of the wave correspond to a sequence of states (resting-activation-inactivation-resting or 0, 1, -1, 0). More complex cases can be found in [10, 15].
Fig. 5. (b) shows very schematically 6 electrodes (1, 2, ...6) and 6 regions (rectangles) of excitable tissue. Each region has an associated wave-source represented by the letter of the region a, b, c, d, e and f. The wave activates (black square, 1) and then inactivates (gray square, -1) the subregions. Regions a and b projects respectively to c and d. The projection fibers (dark gray) have, however, a twist that results in a change in direction of the wave from up-down (in a and b) to right-left (c) or left-right (d).
Suppose that local coordinate systems are conveniently located in each region. If V = 1, and the wave propagate along the X-axis, we can write:
Where s is the total delay of the projection from a to c, as a lineal function of the axonal conduction velocity V'. If p is other delay and l is the length of the axons s = V'l + p.
Fig. 5 (b) shows also that c and d project bilaterally to e and f but the waves are fragmented in this case.
This scenario can represent a simplified case of projections from one neural map to another [5, 7]. As a toy model, it illustrates how simple systems behaves in order to facilitate generalization to more complex cases. Toy models are necessary when the understanding of the system is so difficult that it needs intermediate simplified models, so researchers can grasp and discuss about mechanisms. Future simulations can add, of course, more details; f can be probabilistic and it can have a more complex direction as in Eq. (2), for example.
The model can also illustrate qualitatively what can happen during evoked potentials during demyelination processes, where V' is reduced [16, 17, 18]. The simulation can test the following hypothesis, denoted by H1, H2 and H3:
H1: If all the subregions of a and b are stimulated simultaneously, the wave inside each region disappears but still there are bilateral sequential activations between regions: a-c-e, f and b-d-e, f. The situation is somehow analogous to Fig. 3, where e is the average between electrodes 1 and 2, e' the average between electrodes 3 and 4 and e'' is the average to electrodes 5 and 6. This is also an approximation to the case where V>>V'.
H2: If there is a unilateral demyelination, an asymmetry occurs between left and right waves that propagate downstream (Fig 5 (c)). As the asymmetry increase, the amplitude of the evoked potential between electrodes 5 and 6 decreases and the latency increases.
H3: Evoked potentials, induced by a moving stimulus instead of a single stimulus to the whole region, can result in a more precise estimation of the sources. The application of sequences of stimulus at different intervals and directions results in changes in amplitude and latencies that can give information about the location of the lesions that cause abnormal delays. This can be done for visual and for somatosensory evoked potentials. Graphical analysis of these pairs can show where clinical information about the lesion.
Computational techniques might be necessary in this case. For instance, in the turtle visual cortex, the response at each type of stimulus can be analyzed as contributions to a series of basis images ("modes") [10, 19]. Some modes are, for instance, spatial harmonics that capture rostral to caudal wave propagation. This suggests that decomposition of images obtained in more complex pattern of waves, like that obtained during visual evoked potentials, can then be useful.
In optic neuritis (a condition common in multiple sclerosis, [18]) the EF-amplitude that result when a single eye is stimulated can be smaller respect to the EF-amplitude when the other eye is stimulated. This is because the axonal conduction velocity (V') is reduced due to pathology. For fast stimuli, V can be then comparable to V' and this can produce alteration in the sequence of activation and therefore problems in visual perception and dizziness.
Another issue to discuss is: Are the mechanisms of visual motion detection analogous to the process of wave detection in electrophysiology? Many algorithms proposed for motion processing in visual systems [12] can be implemented in systems for electrophysiological recordings of EEG or ECG. Sensors can be considered photoreceptors or neurons. The reference voltage is also analogous to the background of an image. In this way, the wavefront of a moving depolarization in electrophysiology is a moving edge in visual sciences [12, 13]. The motion detectors proposed by Reichardt and Barlow and Levick [12] can then be used to detect the preferred direction of a wave and its speed.
In an array of electrodes over a surface, values can be interpolated and an electrophysiological image can be constructed [20]. Sequences of these images (a movie) can show the motion and shape of moving electrical objects, like conventional movies show the movements of edges in solid bodies. The estimation of direction, speed, location and form of a 3D-wave inside the brain -based on the processing of 2D electrophysiological images- is analogous to the problem of motion and shape estimation of a solid body from 2D-images in visual systems. The solution is substrate-independent: algorithms and equations can be implemented using neural or engineering resources.
Finally, what is the best way to understand and apply our models and their equations? The toy model we have proposed was designed with 3 goals in mind: be simple and general, illustrate the application of principles and give insight into the mechanisms of formation of the EF-waveforms. Some of the approximations that were used have been recently revisited.
For instance, in a recent controversy, the concept of monopoles is interpreted in physiological and mathematical terms ([21, 22]). For monopoles, EF decays according to the factor 1/r; see Eq. (1) with a = 1. Other models involve a series of terms called the multipolar expansion: (monopole a = 1) + (dipole a = 2) + (quadrupole a = 3) + (octupole a = 4) + (infinite number of other contributions) [20]. On the other hand, at large distances, the EF of a set of charges of equal sign is that of a monopole [20], localized between these charges. Grouping of charges in space-time sets can simplify our models but charges can emerge in uncertain places and times. Determining electric field screening at the scales of T, the decay time constant (T = permittivity/ conductivity) and the Debay length can be difficult [22]. This difficulty adds to the uncertainty in open probability and location probability of ion channels and their associated currents [23]. Although stochastic wavefronts can produce EF-waveforms that look deterministic (Fig 4), at smaller scales, probabilistic models might be necessary. Channel stochasticity must also contributes to the noise that, by resonance, generate the standing waves of the EEG [20].
To explain this, let's consider the EF as the weighted integral of P(r,t) over the brain or heart volume [20]. P(r,t) -a vector- is the current dipole moment of a subregion at location r, containing millions of membrane microcurrent sources. At least some fraction of these microcurrents is generated by the probabilistic opening of ion channels. The stochastic behavior of ion channels might cause some of the effects described by Riera [21], like the formation of fast transients of unbalanced charges (monopoles).
The EF in our model should be then interpreted as the result of the synchronized activation of ionic channels surrounded -in space and time- for electrochemically active charges. Channels also have charged sequences of amino acids themselves (voltage sensors) [7, 9]. All of these electrical particles (ions, channels, polar molecules etc) not only contribute to but also are affected by electric fields. This interaction between fields and particles is so fast and complex that can only be described as a probabilistic interaction [23].
Based on the research of other groups [24, 25, 26] it has been proposed that weak fields (endogenous or exogenous) might involve organized and frequency-dependent trajectories through macromolecular networks that can affect selectively the open probability of calcium-channel complexes [27]. An important issue is that stimulation with exogenous fields should be "friendly" [25, 27, 28]: it should amplify -instead of impose- an ongoing healing process. Ideally, transcranial electric or magnetic stimulation (respectively TES/TMS ) should use the same physiological signals that the brain generates (i.e. exogenous fields should imitate the endogenous fields) and targets subregions that are likely to be activated by the field of the wave itself. To do this, a TES/TMS-stimulus should be applied based on a real-time prediction about the emergence, direction, trajectory, wavefront or duration of these waves (EEG-triggered stimulation [27]). For bilateral waves, if one at least is normal, it can be used to predict the other and stimulate the abnormal side with the goal of reducing the difference (the error in control engineering) between both.
High frequency waves have been proposed in dream states [29]. Process of cross-frequency coupling [30] can organize the flow of information during sleep and the consolidation of memory. Therefore, synchronization pathologies caused by unilateral lesions can result in difficulties in routing information to the appropriate place as the brain classify and redistribute the information and sensory-motor neural activities of the day during sleep [25, 31]. A sequential activation process during sleep permit multiplexing [31] and periodic sensitivity to tiny electrical variations [9, 31]. Subregions can respond to weak EF during these periodic intervals.
The role of temperature in calcium-related healing [24] and plasticity [5] need to be modeled in a frequency-dependent way [26, 28, 32]. Modeling of calcium waves and how they interact with EF-waves is summarized elsewhere [33]. Toy models can predict the changes in calcium because they are indicators of states of modular activity [8]. Rehabilitation therapies for nerve and muscle executed during the day can be more strongly consolidated during sleep using brain stimulation. Recovery processes of the heart during sleep can be stimulated not only by increasing sleep quality but by direct "amplification" of the healing that a good sleep allows.
Although only some of these mechanisms are just now been explored, if we can enhance the restorative and healing effect of sleep with exogenous fields, the benefits will compensate the risks of failure based on mechanisms that are still uncertain.
IV. CONCLUSIONS
- In spite of their simplicity, the importance of extremely simplified "toy-models" is, however, considerable: they complement more detailed computer models because they clearly show us where and when our reasoning is correct and how we can refine it.
- Algorithms for detecting of direction, speed and location of the visual system can be implemented in software for EEG or ECG. Physical objects (3D), images (2D) and neurons in the visual system correspond to "electric objects" (3D-waves), surface potentials and outputs in electrophysiology, respectively. Problems of disparity, correspondence, depth estimation are also common to both. Therefore, methodologies and solutions of vision research (Gabor filters, Laplacian of Gaussians and fuzzy logic [12, 13, 14, 20]) can be useful in electrophysiology.
- Evoked potentials are abnormal in demyelinating diseases like multiple sclerosis [16, 17, 18]. In this disease, demyelination can cause distorted waves that can generate comorbidity and possible unwanted ephaptic effects. Weak exogenous stimulation can boost the emergence, completion, redirectioning and plasticity effects of waves [25, 27, 28].
ACKNOWLEDGMENTS
We thank Advisors, Researchers, Collaborators and Medical Doctors of the International Group of Neuroscience (IGN), Asociación de Esclerosis Multiple (ALEM), EAFIT University and CES University (Medical School).
REFERENCES
[1]. Alexander D., Jurica P., Trengove C., Nikolaev AR., Gepshtein S., Zvyagintsev M., Mathiak K., Schulze-Bonhage A., Ruescher J., Ball T., van Leeuwen C. Traveling waves and trial averaging: the nature of single-trial and averaged brain responses in large scale cortical signals. Neuroimage, 73: 95-112, 2013. [ Links ]
[2]. Hughes J.R. The phenomenon of traveling waves: a review. Clin Electroencephal, 26 (1):1-6, 1995. [ Links ]
[3]. Malmivuo J., Plonsey R. Bioelectromagnetism. Oxford University Press, 1995. [ Links ]
[4]. Massimini M., Huber R., Ferrareli F., Hill F., Tononi G. The Sleep slow oscillation as a traveling wave. J Neurosci, 24(31): 6862-6870, 2004. [ Links ]
[5]. Kandel, E. Principles of Neural Science. 6th Edition, Mc Graw Hill, 2005. [ Links ]
[6]. Buzsaki G., Anastassiou C., Koch C. The Origin of extracellular fields and currents-EEG, EcoG, LFP and spikes. Nat Rev Neurosci, 13: 407-420, 2012. [ Links ]
[7]. Carpenter R.H.S. Neurophysiology. Oxford University Press. New York, NY. 2010. [ Links ]
[8]. Gomez-M. J.F. Ionic currents and metabolism for brain scanners (a three-state model of modular activation). Neural Networks, 13(6): 689-690, 2000. [ Links ]
[9]. Ermentrout G.B, Kleinfeld D. Traveling electrical waves in cortex: insights from phase dynamics and speculation on a computational role. Neuron 29(1): 33-44, 2001. [ Links ]
[10]. Robbins K.A., Senseman D.M. Extracting wave structure from biological data with application to responses in turtle visual cortex. J Comput Neurosci, 16(3): 267-298, 2004. [ Links ]
[11]. Anastassiou C.A, Perin R., Markram H., Koch C. Ephaptic coupling of cortical neurons. Nat Neurosci, 14(2): 217-223, 2011. [ Links ]
[12]. Ulinski P. Neural mechanisms underlying the analysis of moving visual stimuli. Cerebral Cortex. Plenum Press, 13: 283-400, 1999. [ Links ]
[13]. Gomez-Molina J.F., Restrepo A., Molina L. Edge processing: from Gabor filters in V1 to robotic design (applied astrophysiology) in day/night and up-fast vs. down-slow conditions. Society for Neuroscience meeting, San Diego CA, US, Nov 2010. Online sfn.org. [ Links ]
[14]. Rattay F. The basic mechanism for the electrical estimulation of the nervous system. Neuroscience 89(2): 335-346, 1999. [ Links ]
[15]. Knobel R. An Introduction to the Mathematical Theory of Waves. American Mathematical Society, 2001. [ Links ]
[16]. Sand T., Kvaloy M.B., Wader T., Hovdal H. Evoked potentials in clinical diagnosis. Tiddskr Nor Laegefore,. 133(9): 960-965, 2013. [ Links ]
[17]. Sá MJ. Physiopathology of symptoms and signs in multiple sclerosis. Arq Neuropsiquiatr 70(9): 733-740, 2012. [ Links ]
[18]. Toosy A.T., Mason D.F., Miller D.H. Optic Neuritis. Lancet Neurol. 2, 13(1), 83-99, 014 Jan, doi: 10.1016/S1474-4422(13)70259-X. [ Links ]
[19]. Gomez-Molina J.F., Robins K., Senseman D. Differences in the Spatiotemporal dynamics of cortical waves evoked by stationary and moving stimuli. I World Association of modeling meeting and II GENESIS-users meeting. Organizers: James Bower, University of Texas HSCSA and David Beeman University of Colorado at Boulder. 3/31-4/2, 2005. San Antonio, TX, USA. [ Links ]
[20]. Nunes P., Srinivasan R. Electric Fields of the Brain. Oxford University Press, 2006. 2nd Edition. [ Links ]
[21]. Riera J.J., Ogawa T., Goto T., Sumiyoshi A., Nonaka H., Evans A., Miyakawa H., Kawashima R. Pitfalls in the dipolar model for the neocortical EEG sources. J Neurophysiol, 108: 956-975, 2012. [ Links ]
[22]. Riera J., Cabo A. Instantaneous Charge Unbalance in the Brain; a result from Procedural Errors or an Authentic Physical Phenomenon? J Neurophysiol 109, 1684-1685, 2013. [ Links ]
[23]. Gomez-Molina J.F. Ionic channels and long-range electrical signals: a probabilistic interaction. Medical Hypotheses 60(4), 463-467, 2003. [ Links ]
[24]. Escobar I., De Mello W.C., Pérez B. Healing Over and muscle contraction in toad Hearts. Circ Res 31(3), 389-396, 1972. [ Links ]
[25]. Fröhlich F., McCormick D.A. Endogenous electric fields may guide neocortical network activity. Neuron. 15, 67(1), 129-43. 2010 Jul. doi: 10.1016/j.neuron.2010.06.005. [ Links ]
[26]. Ricoy U.M., Frerking M.E. Distinct roles for Cav2.1-2.3 in activity-dependent synaptic dynamics. J Neurophysiol. 15; 111(12), 2404-13. 2014 Jun, doi: 10.1152/jn.00335.2013. [ Links ]
[27]. Gomez-Molina J.F., Ricoy U., Escobar I., Vélez J. How can the open probability of ionic channels and the waveform of a burst be maximized by designing an EEG-triggered sequence of TES/TMS? Society for Neuroscience meeting, Washington DC, online sfn.org 2014. [ Links ]
[28]. Gomez-Molina J.F., Botero LF, Ciro JD, Gomez-Molina A.L. Thermal circuit analogs in the brain and "friendly" stimulation during sleep rhythms: modulation of TMS/TES, Society for Neuroscience meeting, San Diego CA, online sfn.org 2013. [ Links ]
[29]. Llinas R. Ribary U. Coherent 40-Hz oscillation characterizes dream state in humans. Proc. Natl. Acad. Sci. U.S.A. 90 (5), 2078-81, 1993. [ Links ]
[30]. Jirsa Van duller V. Cross-frequency coupling in real and virtual brain networks. Frontiers in Computational Neuroscience, 2013. [ Links ]
[31]. Gómez J.F. Lopera F.J. A Thalamic Electric Oscillator for Interhemispheric Communication. IEEE International Conference on Neural Networks. 377-380, 1997. [ Links ]
[32]. Krishna A., Valdarrabano, Palade P.T-, Clark J.W. Rate-dependent Ca2+ signaling underlying the forcé-frequency response in rat ventricular myocites: a coupled electromechanical modeling study. Theor Bio Med Model, 10, 54, 2013. [ Links ]
[33]. Roberts B.N., Yang P.C., Behrens S.B., Moreno J.D., Clancy C.E. Computational approaches to understand cardiac electrophysiology and arrhythmias. Am J Physiol Heart Circ Physiol 303(7), H766-83, 2012. [ Links ]