INTRODUCCIÓN
Tomando en consideración que las especies frutícolas se deberían cultivar en lugares con una oferta ambiental similar a la de su lugar de origen, los frutales caducifolios deberían cultivarse solamente en condiciones de clima templado. No obstante, las condiciones climáticas en los altiplanos tropicales ofrecen a los frutales de hoja caduca, como el duraznero y el ciruelo, un ambiente en el cual es posible producir una o más cosechas por año (Fischer et al., 2010). Los cultivos de duraznero y ciruelo revisten gran importancia para el departamento de Boyacá, Colombia, dado que según Agronet (2017), se cultivaron en 2014, en Colombia, 1.905 ha en duraznero y 1.281 en ciruelo, de las cuales, Boyacá participó con el 43,4 y 62,1% del área sembrada a nivel nacional en durazneros y ciruelos, respectivamente. En este sentido, Boyacá es considerado el departamento de mayor relevancia en el cultivo de frutales caducifolios en el país, debido a las ventajas comparativas que presenta esta región del trópico alto, como son: clima, suelos, precipitación, acumulación de horas frío, vocación frutícola de los productores y experiencia acumulada de los agricultores (Patiño y Miranda, 2013).
El área foliar es una variable de gran importancia en la mayoría de los estudios agrícolas y fisiológicos involucrados en el crecimiento vegetal (Hunt, 1990), captura de luz, eficiencia fotosintética, respiración, transpiración y respuesta a diferentes tratamientos. La medición del área foliar, se realiza regularmente mediante métodos directos con la ayuda de medidores electrónicos, para lo cual, es necesario retirar las hojas del vegetal, por ser un método destructivo. Además, esta medición, se restringe a la disponibilidad de equipos especializados. Por otro lado, los métodos indirectos son de gran utilidad cuando no se dispone de los respectivos equipos electrónicos (Blanco y Folegatti, 2005). Mediante la utilización de las funciones de predicción de área foliar se puede estimar el área de las hojas sin causar daños a las plantas, y además, este método puede proporcionar a los investigadores, muchas ventajas en experimentos hortícolas, como la estimación del área foliar en la misma temporada de crecimiento de las plantas y de este modo es posible reducir la variabilidad en los resultados de los experimentos (Serdar y Demirsoy, 2006).
Las funciones matemáticas se han utilizado ampliamente con el propósito de estimar el área foliar en diferentes plantas cultivadas. Es así, como Cristofori et al. (2007) obtuvieron modelos lineales simples, precisos y no destructivos para estimar el área foliar en Corylus avellana, utilizando como variables la longitud y el ancho de la hoja, o la combinación de las dos. De igual manera, Peksen (2007) logró modelos lineales para la estimación del área foliar en plantas de Vicia faba, utilizando como variables el largo y el ancho de las láminas foliares. Con una metodología similar, Kandiannan et al. (2009) lograron gran precisión en los modelos calculados para la estimación del área foliar en Zingiber officinale, y por su parte Kumar (2009) realizó el mismo procedimiento con hojas de Crocus sativus.
Cabezas-Gutiérrez et al. (2009) calcularon funciones estadísticas predictivas para el área foliar de Alnus acuminata, Escallonia pendula y Quercus humboldtii. Estos autores resaltan el uso del producto del largo por el ancho de las hojas como variable de la función en todas las especies estudiadas, a pesar de las diferencias morfológicas de sus láminas foliares. Keramatlou et al. (2015) calcularon y validaron diferentes funciones matemáticas para estimar el área foliar en plantas de Juglans regia. Estos autores concluyeron también, que los modelos que involucran el largo y el ancho de las hojas proporcionan estimaciones más precisas del área de las plantas en diferentes genotipos y ambientes, que aquellos basados solamente en la longitud o el ancho, como variables únicas. Así mismo, Pompelli et al. (2012) calcularon una función para predecir el área foliar de Jatropha curcas, en la que utilizaron el producto del largo por el ancho de la hoja como variable independiente, en lugar de utilizar solamente el largo o el ancho de las hojas, ya que cuando utilizaban solo el largo o el ancho como variable independiente, el modelo propuesto se ajustaba a expensas de la heterocedasticidad del comportamiento de la dispersión residual.
El objetivo del estudio fue determinar y validar las funciones de regresión más acertadas para la estimación no destructiva del área foliar en algunos cultivares de duraznero y ciruelo, con el propósito de socializar una herramienta útil en los estudios de fisiología vegetal, fitopatometría, entomología y de rendimiento agronómico en estos cultivares.
MATERIALES Y MÉTODOS
El ensayo se realizó en la granja Tunguavita de la Universidad Pedagógica y Tecnológica de Colombia (UPTC) en Paipa, Colombia, ubicada a 0,5°45’ N y 73°45’ W. La localidad presenta una temperatura promedio de 14,3°C, humedad relativa de 78% y 737,9 mm de precipitación anual. Se seleccionó esta localidad dado que en ella crecen diferentes especies frutícolas caducifolias y siempreverdes con propósitos de producción comercial de fruta, multiplicación de los cultivares e investigación.
Para la medición y estimación del área foliar se tomaron hojas de plantas de ciruelo (Prunus salicina) de los cultivares Gold Fruly, Ecuatoriano, Methley y Horvin. También se tomaron hojas de duraznero (Prunus persica) de los cultivares Dorado, Rubidoux, Diamante y Rey Negro. Los árboles de duraznero y ciruelo tenían una edad aproximada de 15 años. En todos los casos se tomaron hojas que no presentaban daño mecánico ni por problemas sanitarios. De cada cultivar se seleccionaron 100 hojas, y en cada una de ellas se determinó el área foliar mediante un medidor Li-Cor 3000A (Fa. Li-Cor, Lincoln, NE). En cada hoja se midió el área foliar cinco veces, se calculó el promedio y este se dejó como dato definitivo. De este modo, se tomaron 100 mediciones por cada uno de los cultivares. De igual manera, en cada hoja se midió el largo y el ancho mediante una escala de Vernier. Los datos se consignaron en una tabla en la que frente al valor del área foliar de cada hoja, se encontraban los valores del largo y del ancho de la misma, así como también el producto del largo por el ancho de la hoja.
Desde el momento de la colección de las hojas de todos los cultivares en el campo, hasta tener el listado de datos para realizar la validación, transcurrieron alrededor de tres semanas. Con los datos registrados se realizó un análisis de regresión curvilínea (P≤0,01) mediante la aplicación IBM®SPSS®, versión 20.0. Se calcularon todas las funciones de regresión que ofrecía la aplicación y se seleccionó aquella que presentaba el coeficiente de determinación (R 2) más alto. Como variables, se utilizaron, el valor del área foliar determinada con el analizador Li-cor 3000A (Fa. Licor, Nebraska, NE, USA) y el valor del producto del largo por el ancho de la misma hoja. De este modo se calculó una ecuación de regresión para cada cultivar y especie. Posteriormente se tomaron 50 hojas más, diferentes a las anteriores y en ellas se determinó el área foliar con el equipo correspondiente, su largo y su ancho. Esta información se validó con las ecuaciones calculadas anteriormente para la variedad respectiva. Con esta información se realizó una prueba de correlación de Pearson (P≤0,01) entre el área foliar observada con el medidor de área foliar y la estimada con la ecuación.
RESULTADOS
Cultivares de ciruelo ( P. salicina )
Para los cultivares Gold Fruly, Ecuatoriano y Methley, la función de regresión que más se ajustó fue de tipo cuadrático. Por su parte, la información registrada para el cultivar Horvin se ajustó a la función cúbica (Tab. 1). Los valores del coeficiente de determinación (R 2) fluctuaron entre 0,62 y 0,83. El menor valor de R 2 se registró para el cultivar Methley, y los valores más altos los presentaron los cultivares Ecuatoriano y Horvin. En todos los casos, el análisis de regresión dio resultados altamente significativos (P≤0,01) para las funciones evaluadas. Con base en esta información se puede inferir que, de entre los cultivares estudiados, Methley es el que presenta mayor variabilidad en cuanto al tamaño y forma de sus hojas, lo que dio como resultado que los datos calculados no se ajustaran con precisión a los datos observados, dado que este valor representa la proporción de variación explicada por la ecuación de regresión y además, es una medida relativa del grado de asociación lineal entre X y Y. Desde la perspectiva del análisis de regresión, es posible afirmar que el ajuste de las funciones para los cultivares Gold Fruly, Ecuatoriano y Horvin es aceptable, ya que sus valores de R 2 son los más cercanos a 1. Por tanto, para estos tres cultivares, entre el 77 y el 83% de la variabilidad de la variable Y a su promedio es explicado por la función de regresión presentado en la Tab. 1. De este modo, se puede decir que las funciones lineales calculadas son adecuadas para describir la relación que existe entre las variables X (producto del largo por el ancho de las hojas) y Y (área foliar).
Tabla 1 Ecuaciones de regresión en cuatro cultivares de duraznero (P. persica) y de ciruelo (P. salicina) para el cálculo indirecto del área foliar con base en el largo y ancho de las hojas.
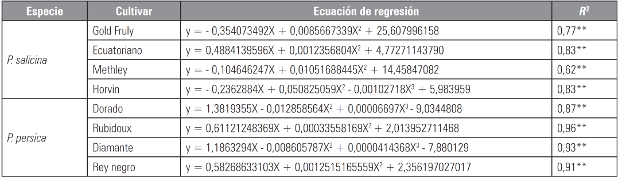
** P≤0,001; Y: área foliar: X: producto del largo por el ancho de la hoja.
Para el caso del cultivar Methley, si bien es cierto que el coeficiente R 2 se encuentra más alejado de 1 que los coeficientes calculados para los demás cultivares de ciruelo, esto no sería motivo de rechazo y la ecuación se puede utilizar para la estimación indirecta del área foliar en este cultivar, no obstante, se debe contar con que los datos obtenidos con el uso de esta ecuación se ajustarían en un menor porcentaje a la realidad (62%), en relación con los otros tres cultivares de ciruelo evaluados.
La información planteada con anterioridad, se observa de manera gráfica en los diagramas de dispersión desarrollados para los cuatro cultivares de ciruelo estudiados y presentados en la Figura 1. Se puede entender que a pesar de que los cultivares Ecuatoriano y Horvin presenten valores similares en cuanto al coeficiente de determinación (R 2 0,83), Horvin presenta menos dispersión de los datos en la Figura 1. En este caso se puede inferir que la función cubica encontrada para ciruelo Horvin expresa de mejor manera la relación entre las variables área foliar (Y) y el producto del largo por el ancho de las hojas (X). Por otro lado, el diagrama de dispersión para el área foliar del cultivar Methley (Fig. 1), muestra que este cultivar, a pesar de ser el que tuvo el menor coeficiente de determinación, del grupo de los cultivares evaluados, su dispersión se asemeja a la del cultivar Ecuatoriano, a pesar de que el R 2 en Methley fue considerablemente inferior (0,62) que el de Ecuatoriano (0,83).
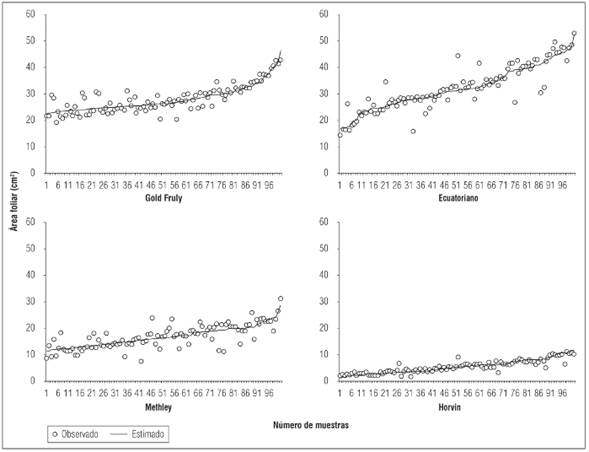
Figura 1 Diagrama de dispersión para los datos observados y estimados en hojas de cuatro cultivares de ciruelo (P. salicina).
Al observar los resultados del cálculo de los coeficientes de correlación de Pearson, la Tab. 2 muestra que el grado de covariación entre dos variables, área foliar (Y) y el producto del largo por el ancho de las hojas (X), relacionadas linealmente oscila entre 0,92 y 0,97 para los cuatro cultivares de ciruelo. Esta información permite inferir que la correlación es positiva y casi perfecta, dado que en la medida que aumenta una de las variables, aumenta la otra. El mayor valor del coeficiente de correlación de Pearson se encontró en el cultivar Ecuatoriano, no obstante, los demás cultivares estudiados presentaron coeficientes muy cercanos a la unidad, lo que indica una dependencia total entre las dos variables.
Cultivares de duraznero ( P. persica )
Para los cultivares Dorado y Diamante, se encontró que la función cúbica fue la que más se ajustó, acorde con el coeficiente de determinación (R 2), mientras que para los datos colectados se ajustaron mejor a la función cuadrática. Los valores de R2 para los cuatro cultivares estudiados osciló entre 0,87 y 0,96, lo cual es un índice de la bondad del ajuste o fiabilidad de las funciones estimadas a los datos observados. Entre los cultivares de duraznero estudiados, Rubidoux presentó el valor de R 2 más elevado (0,96), mientras que el valor más bajo (0,87) se encontró en el cultivar Dorado (Tab. 1). Los cuatro cultivares de duraznero estudiados presentaron valores de R 2 más elevados que los cultivares de ciruelo, lo cual indica que, de las dos especies analizadas, las ecuaciones de regresión calculadas para duraznero serían más confiables que las encontradas para los cultivares de ciruelo, no obstante, todas las ecuaciones son confiables acorde con el hecho de que el valor del coeficiente de determinación sea más cercano a la unidad.
La representación de los diagramas de dispersión presentados en la Figura 2, confirma lo planteado anteriormente para los cultivares de duraznero. Se puede ver que los datos observados no están muy dispersos en relación con la curva estimada, con lo cual se puede inferir el alto grado de dependencia que existe entre las variable área foliar (Y) y el producto del largo × ancho de las hojas (X). Es importante el análisis de los diagramas de dispersión como complemento del simple análisis estadístico puesto que las representaciones gráficas facilitan significativamente el análisis numérico. En este caso, el análisis numérico mostró que el cultivar Rey negro tiene un R 2 de 0,91, mientras que para Rubidoux el R 2 fue de 0,96, no obstante, los diagramas de dispersión para estos dos cultivares muestran un mayor grado de ajuste entre las variables en Rey Negro que en Rubidoux.
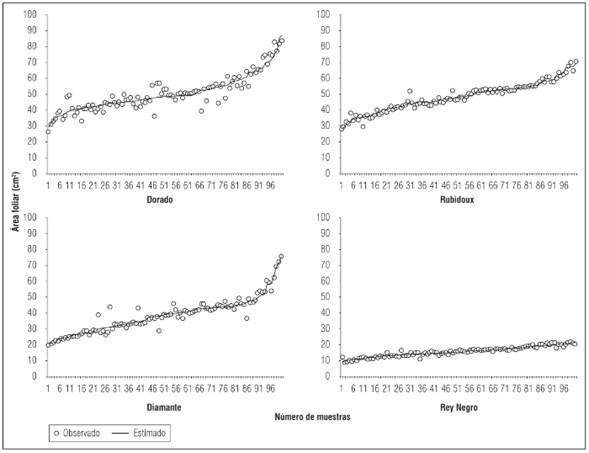
Figura 2 Diagrama de dispersión para los datos observados y estimados en hojas de cuatro cultivares de duraznero (P. persica).
Los coeficientes de correlación de Pearson para los cuatro cultivares de duraznero analizados están en el rango de 0,95 a 0,99, lo que muestra un alto grado de concordancia en sentido directo de las posiciones relativas de los datos en las variables área foliar (Y) y el producto del largo × ancho de las hojas (X). Comparativamente, el rango de los valores encontrados para los coeficientes de correlación de Pearson en los cultivares de duraznero analizados son ligeramente superiores a los calculados para los cultivares de ciruelo, a pesar de lo cual en los cultivares estudiados de ambas especies, los coeficientes de correlación de Pearson presentaron valores superiores a 0,9, lo que indica una alta dependencia entre las dos variables analizadas.
DISCUSIÓN
En botánica, la forma de la hoja es un componente importante de la morfología de las plantas con el propósito de establecer su descripción y taxonomía. Como una de las características más visibles, la forma de la hoja juega un papel importante para la identificación de la planta, dado que las hojas son abundantes en las plantas y tienen diversas formas y períodos de supervivencia más largos que las frutas (Cope et al., 2012). Se han utilizado descriptores para hojas, complementados con análisis discriminantes para identificar tipos de plantas y se ha obtenido aproximadamente un 89,4% de precisión entre las hojas observadas y las referenciadas en los descriptores. En estos estudios de identificación foliar se han utilizado características geométricas básicas que incluyen su aspecto, rectangularidad, circularidad y excentricidad y otras características de forma, tales como el contorno central y la distancia (Neto et al., 2006).
Adicionalmente se menciona que el desarrollo foliar es el resultado de la cooperación de una serie de procesos regulatorios que operan a nivel celular, del tejido y del órgano (Zhang et al., 2007), dando como resultado la forma y tamaño característicos de las hojas para cada material genético. Con base en estos planteamientos, es posible inferir que los rasgos funcionales de las hojas, como su forma, longitud y ancho, entre otros, tienen un fundamento genético y por tanto son bastante estables y confiables como para utilizarlas con el propósito de proponer funciones matemáticas para la estimación del área foliar en las plantas.
En concordancia con la metodología implementada en el presente estudio, se han realizado diferentes investigaciones con el propósito de establecer una relación confiable entre el área de las hojas y las dimensiones foliares en diferentes especies frutícolas como castaña (Castanea sativa) (Serdar y Demirsoy, 2006), avellana (Corylus avellana) (Cristofori et al., 2007), fresa (Fragaria vesca), uchuva (Physalis peruviana), feijoa (Acca sellowiana), mora (Rubus glaucus), curuba (Passiflora mollissima) y brevo (Ficus carica) (Casierra-Posada et al., 2007) y nogal (Juglans regia) (Keramatlou et al., 2015). En estos estudios se ha encontrado una relación muy estrecha entre la longitud, el ancho de las hojas y en área foliar, con coeficientes de determinación (R 2) con valores superiores a 0,9. Los resultados del presente estudio estuvieron en concordancia con algunos de los estudios anteriores sobre el establecimiento de ecuaciones confiables para estimar el área foliar mediante la medición de las dimensiones de las hojas. En estos trabajos se ha concluido que el uso de las dimensiones de las hojas (largo y ancho) resulta acertado para proporcionar estimaciones precisas del área foliar en las hojas de las especies evaluadas, en diferentes genotipos y ambientes (Cristofori et al., 2007).
Se ha observado que existe un alto grado de similitud entre los cultivares de duraznero y de ciruelo cultivados en la misma localidad de la cual se tomaron las muestras para la realización del presente trabajo. En ese sentido, Morillo et al. (2015) evaluaron la diversidad genética de 42 cultivares del género Prunus, entre los que se encontraban los cultivares de duraznero y ciruelo estudiados en el presente trabajo. Entre sus resultados se mencionan bajos niveles de heterocigosidad, justificados en que la mayoría de los cultivares son autocompatibles, lo que da como resultado, una alta probabilidad de autofecundación. Adicionalmente, se menciona que los cultivares de duraznero y ciruelo son poco diversos genéticamente, en lo que se ve reflejado su proceso, su domesticación y su sistema vegetativo de propagación.
Acorde con el dendrograma de los materiales evaluados por Morillo et al. (2015), los cultivares de ciruelo Horvin y Methley tienen un parentesco bastante cercano, no obstante, en la Figura 1 se puede apreciar que Horvin presenta hojas con menor área foliar que Methley, cuyos valores oscilaron entre 8,4 y 10,6 cm2 para Horvin y 12,5-36 cm2 para Methley. Con base en estos planteamientos, se puede justificar el hecho de calcular una función matemática para cada material estudiado, en lugar de utilizar una misma función para diferentes cultivares de la misma especie, dado que a pesar de que los cultivares tengan una afinidad genética muy cercana, como en el caso de Horvin y Methley, las funciones matemáticas que con mayor precisión explican el comportamiento de su área foliar, son diferentes.
En cuanto a los cultivares de duraznero, acorde con el reporte de Morillo et al. (2015), Rubidoux presenta mayor distanciamiento genético con los demás cultivares de duraznero analizados en el presente trabajo, no obstante, el conjunto de hojas colectadas para la toma de información presentaron valores de área foliar entre 28,02 y 70,81 cm2, los cuales estaban cercanos a los registrados para Dorado (26,3-83,4 cm2) y Diamante (22,8-78,4 cm2). El cultivar Rey Negro presentó las hojas con menor área (12,0-25,3 cm2), lo cual se puede observar en la Figura 2. De esta manera se puede inferir que el grado de afinidad genética no es determinante para que el área foliar de los cultivares se encuentren en rangos de área similares, lo que se pudo observar tanto en duraznero como en ciruelo.
El coeficiente de terminación (R 2) se utiliza para establecer la capacidad explicativa de una función matemática de regresión, dado que representa la variabilidad de la variable dependiente que el modelo calculado explica (Arriaza, 2006). Por tanto, en el caso del presente estudio, mientras más se acerca el valor de R 2 a la unidad, la función de regresión será más confiable en la determinación del área foliar (Y) cuando se usa como insumo el valor del producto del largo × ancho de las hojas (X), como lo explican Casierra-Posada et al. (2007) y Cristofori et al. (2007).
Las funciones matemáticas de regresión deben validarse para establecer su confiabilidad en situaciones reales. En este sentido Cristofori et al. (2007) utilizaron un análisis de regresión en el cual la variable dependiente (Y) correspondió al área calculada de las hojas, mientras que la variable independiente (X) era el área medida de las mismas hojas. De igual modo, Peksen (2007) utilizó un análisis de regresión para validar los datos de las funciones matemáticas calculadas, con las mismas variables utilizadas por Cristofori et al. (2007). Al igual que en el presente trabajo Kandiannan et al. (2009) utilizaron el coeficiente de correlación de Pearson para validar las funciones calculadas. Estos autores señalan que la mayoría de las variaciones encontradas para el área foliar en plantas de Zingiber officinale, se podían explicar a través de los modelos en los cuales el largo y el ancho de las hojas estaba involucrado, además, el coeficiente de correlación de Pearson presentó valores superiores a 0,9 para todos los modelos al momento de validar la información calculada con los datos observados, como sucedió en el presente trabajo, en el cual, según la Tab. 2, los valores del coeficiente de correlación de Pearson osciló entre 0,92 y 0,97 para los cultivares de ciruelo, y entre 0,95 y 0,99 en los cultivares de duraznero analizados. Por tanto, dado que el coeficiente de correlación de Pearson permite medir el grado de asociación entre dos variables, al momento de validar el área foliar estimada mediante las funciones matemáticas y el área foliar medida con el analizador de área foliar, es posible asumir, con base en que los valores de este coeficiente mostraron cifras por encima de 0,9, que el área foliar estimada mediante las funciones de regresión, para los cultivares de duraznero y ciruelo analizados tiene un alto grado de ajuste con la realidad.
CONCLUSIONES
Las funciones de regresión para el cálculo del área foliar utilizando como insumo las dimensiones de las hojas (largo y ancho) de diferentes cultivares de duraznero y de ciruelo, presentados en el presente trabajo fueron seleccionados y elegidos por su simplicidad y grado de ajuste a la realidad, al momento de hacer la validación de las ecuaciones. Mediante el uso de estas ecuaciones se pueden producir resultados de gran precisión, al igual que con otras funciones matemáticas de estimación más complejas o mediante el empleo de equipos costosos y sofisticados. Los resultados obtenidos en el presente estudio demostraron que en los cultivares de duraznero y ciruelo analizados puede predecirse el área foliar usando mediciones curvilíneas simples. Las dimensiones de las hojas se pueden medir fácilmente en el campo, invernadero y experimentos en macetas. El uso de estas ecuaciones permitiría a los investigadores realizar mediciones no destructivas o repetidas en las mismas hojas.















