Introdução

Processos de ensino e aprendizagem de habilidades pré-matemáticas e matemáticas têm sido estudados em pesquisas brasileiras fundamentadas nos princípios da Análise do Comportamento (^{Henklain, Haydu, & Carmo, 2017}). Com base, sobretudo, no modelo de rede de relações e equivalência de estímulos, têm-se desenvolvido pesquisas de avaliação e ensino sobre diversos tópicos em matemática, como o conceito de número (Carmo & Galvão, 1999; ^{Monteiro & Medeiros, 2002}; ^{Prado & de Rose, 1999}), a ordenação (^{Miccione, Assis, & Carmo, 2014}; Miccione, Assis, Carmo, & Lopes-Junior, 2014; ^{Souza, Miccione, & Assis, 2012}) e a resolução de problemas (Haydu, Costa, & Pullin, 2006; Haydu, Lorencete, & Eccheli, 2015; Henklain & Carmo, 2013a, 2013b).

Resolver problemas, de acordo com Skinner (1969/1984), é um evento comportamental no qual a manipulação de variáveis relevantes relacionadas ao problema tornam a solução mais provável. ^{Haydu et al. (2006)} destacam que solucionar problemas matemáticos envolve além da discriminação de variáveis relevantes, a aprendizagem de uma linguagem específica com conceitos, sintaxe e símbolos próprios. Assim, o aprendiz pode ter de identificar, por exemplo, o símbolo referente ao tipo de problema a resolver (adição, subtração etc.), a posição da incógnita e outras variáveis relevantes, como a própria forma de apresentação do problema.

Há indícios na literatura de que o ensino de relações de equivalência entre diferentes formas de apresentação de problemas aumenta o desempenho em tarefas de resolução de problemas aritméticos. O ensino geralmente ocorre por meio de procedimentos que utilizam cartões (^{Haydu et al., 2006}; Haydu et al., 2015) e procedimentos informatizados (^{Henklain & Carmo, 2013a}, 2013b). Nesses estudos os problemas foram apresentados na forma de balança, com algarismos e em sentenças escritas. O estudo de Henklain e Carmo (2013a) apresentou, ainda, problemas na forma de coleções.

Autores do design de jogos (^{Klopfer, Osterweil, & Salen, 2009}), da Educação (Kebritchi, Hirumi, & Bai, 2010; Prensky, 2001/201 2) e da Análise do Comportamento (^{Souza & Hübner, 2010}; ^{Haydu & Zanluqui, 2013}) destacam a possibilidade de utilizar jogos como ferramentas de ensino, salientando que muitos estudantes não se mostram engajados com o ensino tradicional e que a familiaridade com os ambientes de jogos poderia favorecer a adesão dos aprendizes.

Apesar da eficácia de ferramentas tradicionais como cartões e softwares para o ensino de relações condicionais, a literatura tem mostrado alternativas viáveis para intervenção. Autores do design de jogos (^{Klopfer, Osterweil, & Salen, 2009}), da Educação (^{Kebritchi, Hirumi, & Bai, 2010}; Prensky, 2001/201 2) e da Análise do Comportamento (^{Souza & Hübner, 2010}; ^{Haydu & Zanluqui, 2013}) destacam a possibilidade de utilizar jogos como ferramentas de ensino, salientando que muitos estudantes não se mostram engajados com o ensino tradicional e que a familiaridade com os ambientes de jogos poderia favorecer a adesão dos aprendizes. Em razão dessas vantagens, estudos sobre a utilização de jogos digitais como ferramentas auxiliares ao ensino de matemática têm sido conduzidos para o ensino de resolução de problemas (^{Chang, Wu, Weng, & Sung, 2012}; Kebritchi et al., 2010), senso numérico (^{Pope & Mangran, 2015}), conhecimento conceitual e habilidades com números racionais (Chang, Evans, Kim, Norton, & Samur, 2015; ^{Kiili, Devlin, Pertulla, Toumi, & Lindstedt, 2015}), geometria plana (^{Vankús, 2008}), entre outros.

Apesar de os resultados encontrados em pesquisas indicarem o potencial de jogos educativos, há também discussões sobre a falta de embasamento teórico no desenvolvimento e avaliação dessas ferramentas (^{All, Castellar, & Van Looy, 2014}). ^{Van Eck (2006)} destaca a necessidade do uso de teorias de aprendizagem para melhorar a eficácia dos jogos educativos. Algumas aproximações entre a elaboração e uso de jogos educativos e princípios da Análise do Comportamento têm sido feitas recentemente (^{Linehan, Roche, Lawson, Doughty, & Kirman, 2009}; ^{Perkoski & Souza, 2015}).

A possibilidade de combinar jogos ou brincadeiras com procedimentos de MTS (matching to sample) foi discutida por ^{Haydu e Souza (2012)} que enfatizaram a viabilidade de essas tecnologias aumentarem o engajamento dos jogadores nas tarefas. Alguns jogos analógicos foram desenvolvidos e testados com base nos modelos de rede de relações e equivalência de estímulos, utilizando também procedimentos de MTS. Os modelos de rede de relações e equivalência de estímulos guardam muitas semelhanças entre si, sobretudo por sua relação com o processo comportamental de discriminação condicional. O procedimento geralmente utilizado para estabelecer discriminações condicionais é o de MTS, a partir do qual estímulos-modelo (condicionais) são apresentados com estímulos de comparação (discriminativos) e as respostas são reforçadas de acordo com um dos estímulos-modelo. Pressupõe-se que o ensino de um número mínimo de relações favoreça a emergência de outras que não foram diretamente ensinadas.

Nos estudos de ^{Haydu e Zanluqui (2013)}, ^{Godoy, Alves, Xander, Carmo e Souza (2015)} e ^{Gris, Alves, Assis e Souza (2017)} foram estabelecidas discriminações condicionais para ensino de relações matemáticas e monetárias. Esses estudos apresentam avaliações diretas do repertório dos participantes que descrevem a aprendizagem ao longo das intervenções, demonstrando a viabilidade dos jogos em relação ao cumprimento de seus objetivos de ensino. Não foram avaliados, entretanto, outros aspectos dos jogos, observáveis na interação do jogador com o jogo, como a usabi-lidade e o engajamento.

A compreensão de engajamento, enquanto predisposições para permanecer jogando, permite o desenvolvimento de avaliações diretas do comportamento. Por meio dessa compreensão infere-se engajamento a partir de classes de comportamentos que indicam maior probabilidade de o jogador permanecer na atividade, tais como falar positivamente sobre o jogo, permanecer na tarefa na presença de atividades concorrentes etc. (^{Gris & Souza, 2016a}). Em relação à usabilidade, as medidas são utilizadas para verificar se os objetivos de interação do usuário com o sistema são alcançados (^{Cybis, Betiol, & Faust, 2010}). Para tanto, são avaliados aspectos de eficácia que indicam o número e a qualidade dos objetivos alcançados, aspectos de eficiência que indicam a quantidade de recursos dispensados (tempo, esforço físico e cognitivo etc.) e a satisfação frente aos objetivos alcançados (Associação Brasileira de Normas Técnicas, 2002). Assim como em softwares em geral, nos jogos digitais as avaliações de usabilidade são realizadas para verificar se o sistema (jogo) é intuitivo o suficiente para que o jogador passe a maior parte do tempo executando com sucesso ações para alcançar os objetivos propostos pelo jogo e não emitindo quaisquer outras respostas. Para efeito do presente estudo, engajamento refere-se às classes de comportamento que indicam maior probabilidade de o jogador permanecer na tarefa e usabilidade refere-se aos comportamentos que indicam a aprendizagem das regras e da mecânica do jogo, além daqueles relacionados à qualidade com que as jogadas são realizadas.

A partir da literatura apresentada, observa-se que o ensino de relações condicionais tem se mostrado um procedimento eficiente para o ensino de diferentes habilidades matemáticas.

A partir da literatura apresentada, observa-se que o ensino de relações condicionais tem se mostrado um procedimento eficiente para o ensino de diferentes habilidades matemáticas. Considerando a importância do desenvolvimento de tecnologias educacionais que auxiliem o ensino da matemática, a eficiência de procedimentos baseado no modelo de redes de relações e a possibilidade de utilizar jogos digitais, o presente estudo teve por objetivo avaliar os efeitos do ensino de relações condicionais entre numerais, conjuntos de pontos e duas diferentes formas de apresentação de problemas de adição (com algarismos e na forma de balança) promovidos pelo jogo digital Korsan, sobre a resolução de problemas de adição com algarismos e na forma de balança bem como o engajamento produzido pelo jogo e sua usabilidade.

Método

Local, Materiais e Instrumentos

Sala cedida por uma escola estadual, com mesa e cadeiras, iluminação apropriada (janelas e lâmpadas) e na qual, não houve circulação de pessoas estranhas à coleta de dados. Foram utilizados para registro e análise de dados, caneta, filmadora, tripé e notebook com acesso à Internet. Para as atividades concorrentes usou-se lápis de cor, giz de cera, papel, canetinhas, giz e quadro negro, raquetes e bolinhas de tênis de mesa. Para a avaliação de habilidades (Pré-teste, Sondas, Pós-testes e Follow up) foram utilizados jogos "Lince: enterrando tesouros" adaptados para avaliar resolução de problemas de adição (com algarismos e na forma de balança)¹. Na intervenção empregou-se o jogo de dominó digital adaptado Korsan (^{Gris e Souza, 2016b}) para o ensino e teste de relações condicionais matemáticas. A Figura 1 apresenta a interface do primeiro protótipo digital do Jogo Korsan (A, B, C, D), os exemplos de faces dos dominós do jogo (E) e os Tabuleiros dos jogos adaptados "Lince: enterrando tesouros" para a avaliação de resolução de operações de adição com algarismos (F) e na forma de balança (G).

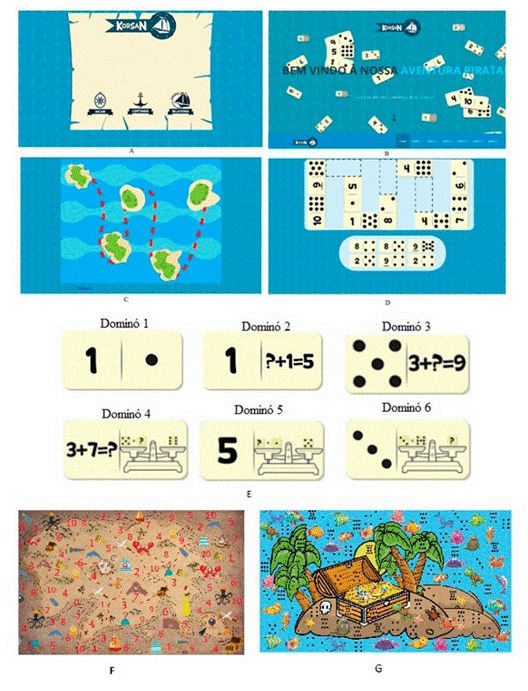
Figura 1 Imagens da interface do primeiro protótipo digital do Jogo Korsan (A, B, C, D), de exemplos de faces dos dominós do jogo (E) e dos Tabuleiros adaptados "Lince: enterrando tesouros" para a avaliação de resolução de operações de adição com algarismos (F) e na forma de balança (G). 

Na intervenção foi empregado o jogo digital Korsan², que tem por objetivo o ensino de resolução de problemas. O enredo do jogo é de uma aventura pirata na qual o participante passa por ilhas, rezspondendo aos desafios. O jogo é composto por um cenário principal (Figura 1, C) no qual são apresentados seis mapas que correspondem às fases de ensino e teste de relações condicionais. Cada mapa apresenta cinco ilhas. Em cada ilha, uma trilha de dominós com três lacunas é apresentada (Figura 1, D). Cada ilha ensina ou testa uma determinada relação (e.g., AB e BA), totalizando 30 relações ensinadas ou testadas (e.g., cinco ilhas nas quais, em cada uma delas, três relações AB e três BA são ensinadas juntamente, uma em cada face da peça de dominó).

A característica de um jogo de dominó pressupõe que seja possível emparelhar peças (estímulos-comparação) de ambos os lados de uma peça já apresentada (estímulo-modelo). No jogo Korsan existem trilhas pré-programadas e para emparelhar corretamente a peça, o jogador deve realizar os cálculos de ambos os lados. Isso foi programado para garantir que o jogador não realize o emparelhamento sem atentar para um dos lados da peça. Os participantes foram expostos aos seguintes estímulos experimentais: numerais impressos (A), conjuntos de pontos (B), problemas de adição com algarismos (C) e problemas de adição na forma de balança (D). Nas classes C e D a posição da incógnita foi variada em a, b e c. Cada dominó apresentava duas classes de estímulos, uma em cada face (Figura 1, E).

Procedimento

Os participantes foram selecionados por indicação da escola, desde que atendessem aos critérios estabelecidos no Pré-teste. O estudo foi conduzido em fases de avaliação de resolução de problemas de adição (Pré-teste, Sondas, Pós-teste e Follow-up) e intervenção (ensino e teste de relações condicionais). As sessões de jogo eram realizadas individualmente com cada participante e gravadas. A Tabela 1 apresenta uma síntese do procedimento empregado com os participantes.

Tabela 1 Síntese do procedimento: fases e atividades programadas 

Avaliação da resolução de problemas de adição. O participante era apresentado a um tabuleiro adaptado do jogo Lince com numerais ou conjuntos de pontos e recebia a seguinte instrução: "- Olá [nome do participante], esse é um tabuleiro para esconder tesouros de piratas. Sua missão é enterrar os números que são o seu tesouro. Você vai receber vários cartões com continhas e terá de encontrar a resposta para cada uma delas nesse tabuleiro. Quando encontrar, esconda o número com uma dessas fichas que tem um "x" para marcar o lugar onde seus tesouros estão escondidos. Preste atenção para resolver corretamente, pois eu não vou lhe dizer se as respostas estão corretas. Se não souber a resposta, esconda seu tesouro em outro lugar". A pesquisadora distribuía para o participante 30 cartões com problemas de adição com algarismos ou na forma de balança e 30 fichas para marcar as respostas. Havia 10 cartões com problemas de adição com incógnitas na posição a, 10 na posição b e 10 na posição c. Na avaliação de resolução de problemas com algarismos, a pesquisadora apresentava os cartões e o participante deveria procurar no tabuleiro adaptado do jogo Lince (Figura 1, F) o número correspondente à resposta do problema previamente sorteado e marcá-la com uma ficha. Na resolução de problemas na forma de balança, o participante deveria localizar em outro tabuleiro adaptado do jogo Lince (Figura 1, G) o conjunto de pontos correspondente às respostas. Não havia consequências programadas para erro ou acerto. No Follow up além da atividade comum às outras avaliações foram apresentados individualmente aos participantes problemas com algarismos e na forma de balança com incógnitas nas posições a, b e c e solicitou-se que os mesmos explicassem como resolveriam cada problema, a fim de verificar se os participantes seriam capazes de descrever o algoritmo de resolução dos problemas.

Ensino e teste de relações condicionais. Inicialmente foram ensinadas as relações entre numerais e conjuntos de pontos (AB/BA) e entre numerais e problemas de adição com algarismos (AC/CA) [Ensino 1]. Foram testadas as relações entre conjuntos de pontos e problemas de adição com algarismos (BC/CB) [Teste 1]. Posteriormente, foram ensinadas as relações entre problemas de adição com algarismos e problemas de adição na forma de balança (CD/DC) [Ensino 2]. Finalmente, foram testadas as relações entre problemas de adição na forma de balança e numerais (AD/DA) e entre problemas de adição na forma de balança e conjunto de pontos, relação BD/DB [Teste2].

No início da intervenção, o participante era apresentado ao jogo pela pesquisadora que informava como as tarefas seriam realizadas: "- O nome desse jogo é Korsan, e isso quer dizer "Pirata" em outra língua. Você vai jogar com dominós e deverá achar as respostas certas para passar por todos os mapas do jogo". A pesquisadora fazia a leitura das frases que apareciam na tela para todos os participantes, que apresentavam repertórios de leitura variados. A frase de entrada do jogo informava: "- Bem-vindo à nossa aventura pirata! Clique na âncora e embarque nesse desafio". O participante era instruído a clicar na âncora e, em seguida, na primeira ilha do primeiro mapa que correspondia ao ensino das relações AB/BA. Nas fases de ensino de relações condicionais, eram fornecidas consequências às respostas dos jogadores. Em caso de emparelhamento correto, a pesquisadora dizia "- Muito bom!" e, em caso de emparelhamentos incorretos, uma janela de correção aparecia na tela de jogo com a frase "Ops! Não é essa peça". Ao completar cada ilha (emparelhar três peças) era apresentada na tela uma caixa de texto com a mensagem "Parabéns". Caso uma ou mais peças fossem emparelhadas incorretamente, o participante era instruído pela pesquisadora a jogar novamente na mesma ilha do mapa, até que as peças fossem jogadas corretamente. Foi adotado um procedimento de correção de ensino que previa a repetição de jogadas com as peças anteriormente emparelhadas incorretamente até que as três peças (seis relações) da ilha fossem emparelhadas de maneira correta. Por exemplo, se na primeira tentativa com um dominó o participante emparelhasse incorretamente uma peça, ele teria de repetir a mesma "ilha" do jogo na sessão posterior (eram requeridos 100% de acertos nas jogadas para avançar no estudo); na segunda tentativa com o mesmo dominó, a peça emparelhada incorretamente na rodada anterior, após ser corretamente jogada, era "roubada" pelo caranguejo (um caranguejo passava pela tela de jogo e uma caixa com o texto: "Ops! O caranguejo roubou a sua peça!" aparecia sobre os dominós), exigindo que o participante realizasse a jogada novamente. Ao final de cada fase de ensino das relações condicionais, feedback era fornecido aos participantes. Caso todas as peças fossem emparelhadas corretamente, a pesquisadora falava: "-Parabéns! Já podemos ir para a próxima ilha". Caso alguma peça fosse emparelhada incorretamente a pesquisadora informava: "-Tivemos um problema e será necessário jogar novamente essa ilha" e o participante repetia a sessão até que todas as peças fossem corretamente emparelhadas. Nos testes de relações condicionais, a pesquisadora informava aos participantes que não poderia auxiliá-los, e que ao final do mapa (após emparelhadas todas as peças de todas as ilhas), ele seria informado sobre a necessidade de repetir alguma ilha. Assim, caso o participante acertasse todas as tentativas programadas, a pesquisadora dizia: "-Parabéns, já podemos ir para o próximo mapa" e o ensino ou teste seguinte era conduzido. Caso houvesse erro em uma ou mais tentativas, a pesquisadora informava ao final do mapa, quais as ilhas (correspondentes às jogadas incorretas) deveriam ser jogadas novamente. O participante repetia as sessões até acertar 100% dos emparelhamentos, sem consequências programadas.

Avaliação de usabilidade e engajamento. Foi realizado um registro categorizado dos comportamentos emitidos pelos participantes durante o jogo. O registro foi feito empregando-se nove categorias adaptadas dos estudos de ^{Perkoski (2015)} e ^{Gris e Souza (2016a)}. Para avaliar usabilidade, as categorias utilizadas foram: perguntas do participante sobre o funcionamento do jogo (PJ) e solicitação de ajuda pelo participante para executar as ações do jogo (SA). Para a avaliação de engajamento foram utilizadas três categorias que dão indícios de engajamento do jogador: comentários positivos sobre o enredo/história do jogo (CH), comemorar (CM) e demonstrar aprovação (DA). Finalmente, foram utilizadas quatro categorias de comportamentos que dão indícios de baixo engajamento: comentários negativos sobre o jogo (CN), comentários sobre assuntos alheios ao jogo (CA), solicitar para interromper a atividade (SI) e solicitar para trocar de atividade (TA). Durante toda a intervenção foram programadas atividades concorrentes ao jogo, pela disponibilização de materiais dispostos sobre a mesma mesa na qual eram realizadas as sessões com o jogo. Essas atividades foram planejadas para fornecer uma medida adicional para a avaliação de engajamento no jogo.

O registro categorizado de comportamentos foi feito pela pesquisadora e por uma observadora independente que assistiam às gravações das sessões. A observadora passou por uma sessão de treinamento na qual foi realizada a categorização conjunta de um trecho de uma sessão de jogo com o auxílio da descrição dos comportamentos a serem observados. Dúvidas foram esclarecidas e discutidas. A observadora externa realizou o registro de 31% das sessões e a porcentagem de concordância absoluta (número de vezes em que as observadoras concordaram/número total de ocorrências) entre as observadoras foi de 85,5 %.

Delineamento Experimental

Foi adotado o delineamento de linha de base múltipla entre sujeitos e, portanto, o ensino de relações condicionais foi introduzido em diferentes momentos para cada dupla de participantes (^{Kazdin, 1982}). Assim, dois participantes (P3 e P4) foram mantidos na condição de linha de base até que o ensino AB/BA, AC/CA e o teste BC/ CB fossem concluídos para os outros participantes (P1 e P2). Em seguida, o ensino de relações condicionais foi introduzido para segunda dupla de participantes.

Resultados

Serão apresentados inicialmente os resultados da avaliação do cumprimento dos objetivos de ensino com base nos resultados do ensino e teste de relações condicionais e da avaliação de resolução de problemas de adição. Posteriormente serão apresentados os resultados referentes às avaliações de usabilidade e engajamento, com base nos dados de observação direta e registro categorizado dos comportamentos emitidos durante as sessões.

Avaliação do Cumprimento dos Objetivos de Ensino

O número total de emparelhamentos necessários para atingir o critério de aprendizagem variou em razão da necessidade de repetição de jogadas decorrentes dos erros de cada participante. A Tabela 2 apresenta o número de acertos dentre o número total de emparelhamentos e as porcentagens de acertos dos participantes.

Tabela 2 Número de jogadas corretas, número total de jogadas e porcentagens de acertos realizadas durante o ensino e teste (sombreado) de relações condicionais 

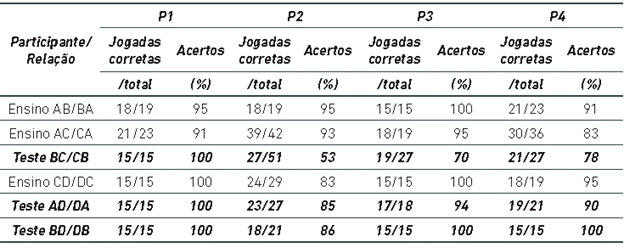
O P1 foi o participante que concluiu a intervenção realizando o menor número de emparelhamentos (102), ao repetir apenas emparelhamentos programados no ensino das relações AB/BA e AC/CA. O P2, por sua vez, foi o participante que precisou do maior número (189) total de emparelhamentos. Para esse participante, após duas tentativas com baixas porcentagens de escolhas consistentes com as programadas para o conjunto de peças que compunham o teste da relação BC/CB, optou-se por retornar ao ensino das relações AC/CA para posteriormente retornar ao teste. Observou-se que esse participante, com frequência, errava o emparelhamento das peças, pois resolvia o problema apresentado na peça para apenas um dos lados da lacuna. Para o P3, foi necessário repetir emparelhamentos para o ensino das relações AC/CA e do teste das relações BC/CB e AD/DA, enquanto para o P4, com exceção do teste das relações BD/DB, foi necessário repetir emparelhamentos em todas as sessões. Todos os participantes apresentaram 100% de acertos nos emparelhamentos da última sessão para todas as relações ensinadas e 100% de escolhas consistentes com as experimentalmente definidas como corretas nas relações testadas. Quanto à duração da intervenção, o P1 necessitou menor tempo para concluir o ensino e teste de todas as relações (1h 54 min e 1seg) em relação aos demais participantes, que concluíram as sessões em aproximadamente 3 horas (3h 26 min e 7s para o P2; 3h 27min e 47s para o P3; e 3h 13 min e 38s para o P4). O tempo necessário para concluir apenas as sessões de ensino foi de 59min e 11s para o P1, 2h 4min e15s para o P2, 1h 41min e 59 s para o P3 e 1h 41min e 15s para o P4.

Foi avaliado também o efeito do ensino e teste das relações condicionais sobre o repertório de resolver problemas de adição com algarismos e na forma de balança. A Figura 2 apresenta os resultados do Pré-teste, Sondas, Pós-teste e Follow up para os problemas de adição com incógnitas nas três posições (a, b e c).

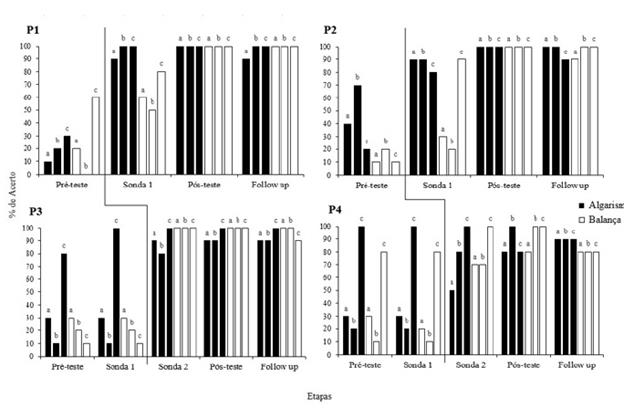
Figura 2 Porcentagem de acertos nos problemas de adição com algarismos e na forma de balança e incógnitas nas diferentes posições ao longo do estudo. A linha preta indica o início da intervenção para cada participante. 

Todos os participantes apresentaram desempenho geral inferior a 60% no Pré-teste, sendo que o P1 e o P3 apresentaram desempenhos inferiores a 30% de acertos em todos os tipos de problema, com exceção dos problemas com algarismos com incógnita na posição c. Não houve mudanças expressivas no desempenho do P3 e do P4, que foram mantidos em linha de base por mais tempo, antes do início da intervenção.

Após o início da intervenção observou-se aumento nas porcentagens de acertos na resolução dos problemas para todos os participantes. No Pós-teste, o P1 e o P2 apresentaram 100% de acertos, enquanto o P3 apresentou 90% de acertos na resolução de problemas com algarismos com incógnitas nas posições a e b e 100% de acertos nos demais problemas. O P4 resolveu corretamente 80% dos problemas com algarismos com incógnitas nas posições a e c e na forma de balança com incógnita na posição a. Para os demais problemas, o P4 apresentou 100% de acertos no Pós-teste. Foi realizado Follow up com cada participante após 36, 35, 49 e 51 dias, respectivamente, para o P1, o P2, o P3 e o P4. Todos os participantes apresentaram porcentagens de acertos superiores a 80% para todos os tipos de problemas com incógnitas em todas as posições nessa avaliação e descreveram o algoritmo de resolução para os dois tipos de problemas com incógnitas em todas as posições.

Avaliação do Engajamento e Usabilidade

Os comportamentos registrados durante as sessões com o jogo Korsan foram separados em três categorias que incluem categorias relacionadas a engajamento, quatro categorias que incluem baixo engajamento e duas categorias para avaliar usabilidade. A Figura 3 ilustra a frequência acumulada dos comportamentos registrados que incluem categorias relacionadas a engajamento e a usabilidade durante as fases do jogo. Os comportamentos que indicam baixo engajamento ocorreram em menor frequência e, por isso, não são ilustrados na figura.

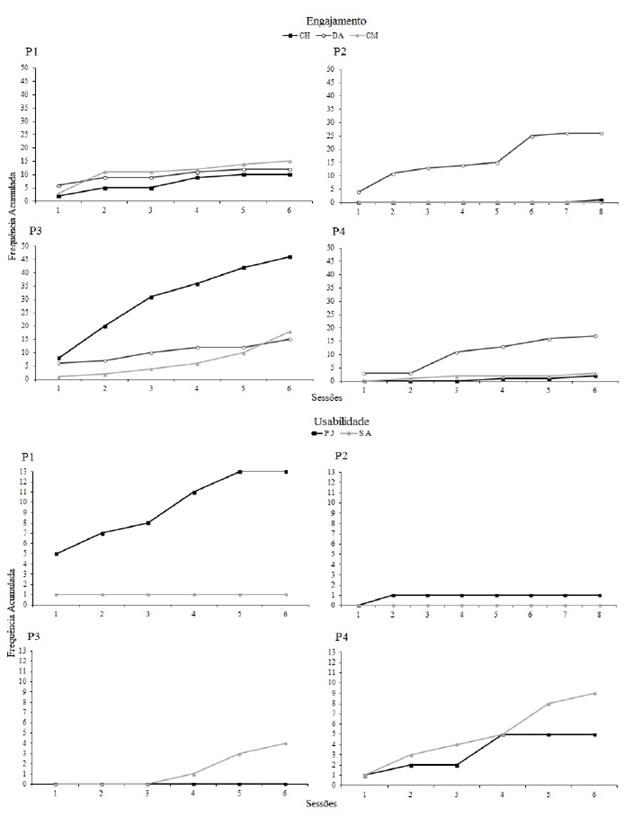
Figura 3 Frequência acumulada dos comportamentos registrados para a avaliação de engajamento e usabilidade. Sendo: CH (comentários sobre o enredo/história), DA (demonstrar aprovação), CM (comemorar), PJ (perguntas sobre o jogo) e SA (solicitar ajuda), durante as fases do jogo/experimento. 

Quanto ao engajamento, o P1 emitiu comportamentos de comemorar em maior frequência, enquanto demonstrar aprovação foi a classe emitida com maior frequência por P2 e P4. O P3 foi o participante com maior ocorrência de comportamentos que indicam engajamento, emitindo 46 comentários sobre o enredo e 18 ocorrências do comportamento de comemorar. Apenas o P2 não emitiu o comportamento de comemorar. A respeito dos comentários sobre o enredo do jogo, cabe destacar que sete dos 10 comentários emitidos pelo P1 eram a respeito do caranguejo que "roubava" as peças, assim como o único comentário do P2 e um dos dois comentários do P4. Apenas o P3 comentou majoritariamente sobre outros aspectos da história do jogo que não o caranguejo. Observou-se a emissão de comportamentos de pelo menos uma das categorias que indicam bom engajamento até a última sessão para todos os participantes.

Quanto aos comportamentos que indicam baixo engajamento, nenhum participante solicitou para trocar de atividade durante o jogo, mesmo com outros materiais disponíveis sobre a mesa. Apenas o P3 (três vezes a partir da terceira sessão) e o P4 (uma vez na segunda sessão) solicitaram para interromper a atividade. O P2 emitiu apenas um comentário negativo e um comentário sobre assuntos alheios ao jogo. Os comentários emitidos em maior frequência pelo o P1, o P3 e o P4 eram sobre assuntos alheios ao jogo.

Quanto à usabilidade, a alta frequência de perguntas sobre o funcionamento do jogo e a emissão desse tipo de comportamento até a penúltima sessão do P1 podem indicar que as regras não estavam claras para este participante. Ainda que as fases de ensino e teste de relações condicionais fossem semelhantes, as relações jogadas eram distintas e o P1 manteve o comportamento de perguntar sobre como emparelhar as peças até a quinta sessão. Resultados semelhantes não foram encontrados para os demais participantes, como se observa a partir da estabilidade da curva PJ. Em relação à solicitação de ajuda para realizar ações do jogo (arrastar peças), o P1 solicitou ajuda uma vez, o P3 três vezes e o P4 nove vezes. O P3 e o P4 solicitaram ajuda inclusive nas últimas sessões, o que indica que o problema não foi resolvido pela prática com o jogo. Esse número, entretanto, é considerado baixo, uma vez que o número mínimo de peças emparelhadas durante as seis fases de ensino ou teste do jogo era de 90, sem considerar repetições em razão de erros. Um dado que confirma essa informação foi obtido a partir do registro da porcentagem de jogadas precisas, nas quais os participantes obtiveram sucesso em emparelhar peças na primeira tentativa. O P1 jogou com precisão 83% das peças, o P2 92,1%, o P3 90,9% e o P4 88,9%.

Discussão

A melhora no desempenho de todos os participantes após a intervenção corrobora os resultados de pesquisas que produziram o ensino de relações condicionais com diferentes formas de apresentação de problemas e com incógnitas em diferentes posições (^{Haydu et al. 2006}; Haydu et al., 2015, ^{Henklain & Carmo, 2013a}, 2013b). Quanto à posição da incógnita, observou-se que antes da intervenção, o P1, o P3 e o P4 apresentavam menores porcentagens de acertos quando a incógnita estava na posição a e b. Esses resultados estão de acordo com a literatura (^{Hiebert, 1982}).

Para vencer as partidas do jogo Korsan, os jogadores deveriam identificar e relacionar estímulos específicos como numerais e conjuntos de pontos. Para solucionar os problemas de adição, alguns comportamentos precorrentes necessários envolviam a identificação da posição da incógnita, o tipo de operação, estabelecer estratégias diferentes para resolver problemas com as incógnitas em cada posição, além da identificação das lacunas nas trilhas de dominó, que exigiam que o participante atentasse para ambos os lados. O arranjo de contingências programadas para o jogo teve por base o ensino de relações condicionais por meio do procedimento de MTS com a apresentação de dois modelos a cada tentativa programada. O ensino de algumas relações (AB/BA, AC/CA e CD/DC) em períodos considerados curtos (em média 2 horas) possibilitou a aprendizagem de outras (BC/CB, AD/DA e BD/DB) que não foram diretamente ensinadas, conforme pressupõe os modelos de redes de relações e equivalência de estímulos (^{Sidman & Tailby, 1982}) além da resolução de problemas de adição em contexto diverso ao do jogo (Sondas).

A melhora no desempenho de todos os participantes após a intervenção corrobora os resultados de pesquisas que produziram o ensino de relações condicionais com diferentes formas de apresentação de problemas e com incógnitas em diferentes posições (^{Haydu et al. 2006}; Haydu et al., 2015, ^{Henklain & Carmo, 2013a}, 2013b).

A categorização dos comportamentos mostrou maior frequência das categorias que indicam engajamento do que de comportamentos que dão indícios de falhas em manter o jogador na atividade. Apesar da variabilidade do tipo e frequência dos comportamentos observados entre os participantes, observou-se que nenhum deles solicitou a troca de atividade, mesmo tendo outras atividades disponíveis durante as partidas.

A partir da observação do comportamento dos participantes P3 e P4 que permaneceram em linha de base enquanto outros participantes passavam pelo ensino, verifica-se que a mudança de comportamento ocorreu apenas após o início do ensino. Os participantes foram capazes, também, de descrever algoritmos para a resolução de problemas de adição com incógnitas nas posições a, b e c. Cabe ressaltar que as descrições de como os emparelhamentos deveriam ser realizados no início das fases de ensino, podem ter favorecido o cumprimento das tarefas pelos participantes.

A categorização dos comportamentos mostrou maior frequência das categorias que indicam engajamento do que de comportamentos que dão indícios de falhas em manter o jogador na atividade. Apesar da variabilidade do tipo e frequência dos comportamentos observados entre os participantes, observou-se que nenhum deles solicitou a troca de atividade, mesmo tendo outras atividades disponíveis durante as partidas. Esse resultado é similar ao observado na avaliação do protótipo físico do jogo Korsan (^{Gris & Souza, 2016a}). O registro categorizado de comportamentos foi adaptado de protocolos para avaliações com versões analógicas de jogos que promoviam a interação entre pesquisador e participante, diferente da interação dos participantes preponderantemente com o jogo digital utilizado nessa pesquisa. Os comportamentos evocados por diferentes interações são também diversos e isso levou a inclusão das classes de comportamentos demonstrar aprovação, comemorar, solicitar para interromper a partida e solicitar para trocar de atividade.

A inclusão da classe "demonstrar aprovação", por exemplo, fez-se necessária a partir da observação das filmagens das primeiras sessões nas quais se observou que o P2 não emitia verbalizações sobre o jogo, embora houvesse a ocorrência de outros comportamentos que indicavam o engajamento na tarefa como sorrir ao emparelhar corretamente uma peça. A adaptação das categorias de registro objetivou tornar o protocolo mais sensível às interações dos participantes com um jogo digital, jogado individualmente, que são diferentes daquelas em jogos cuja interação entre jogadores é programada no processo de design. A necessidade de adaptações indica que a elaboração de protocolos de avaliação das características dos jogos deve levar em consideração as especificidades de cada ferramenta, uma vez que os estímulos apresentados e as contingências planejadas podem ser diferentes.

A ausência de alguns elementos do enredo e da estética do jogo pode ter influenciado os resultados da avaliação do engajamento. De acordo com Schell (2008/2011), os elementos fundamentais de um jogo são tecnologia, mecânica, estética e enredo, sendo todos igualmente importantes e interdependentes. Na versão do jogo utilizada nesse estudo não foram incluídos uma narrativa elaborada, o personagem pirata, as imagens dos tesouros conquistados e outros elementos que estavam presentes na avaliação do protótipo físico e na qual se observou bom engajamento do participante (^{Gris & Souza, 2016a}). Isso pode explicar a baixa frequência dos comentários sobre o enredo do P2 e do P4 e predominância dos comentários sobre o caranguejo - único personagem presente - pelo P1, o P2 e o P4.

Quanto à avaliação de engajamento, ressalta-se ainda, que a busca por medidas diretas de observação do comportamento do jogador durante as partidas é coerente com os procedimentos de pesquisa analítico-com-portamentais (^{Perkoski & Souza, 2015}), embora difiram das avaliações geralmente conduzidas dos jogos.

Quanto à avaliação de engajamento, ressalta-se ainda, que a busca por medidas diretas de observação do comportamento do jogador durante as partidas é coerente com os procedimentos de pesquisa analítico-comportamentais (^{Perkoski & Souza, 2015}), embora difiram das avaliações geralmente conduzidas dos jogos. Ao mapear os procedimentos empregados para avaliação da efetividade da aprendizagem baseada em jogos digitais (digital game based learning, DGBL), ^{All et al. (2014)} indicaram que o engajamento promovido por jogos educativos é citado em avaliações de motivação realizadas principalmente por meio de questionários. Autores como ^{Wouters, Van der Spek e Oostendorp (2009)} afirmam que, apesar dos relatos de que os jogos motivam os jogadores e produzem engajamento, em razão da forma como isso é avaliado não há evidência convincente desse fenômeno. Os resultados obtidos nesse estudo indicam a viabilidade de planejar avaliações por meio de observações diretas do comportamento dos jogadores.

A avaliação de usabilidade indicou que as regras dos emparelhamentos nas diferentes fases do jogo poderiam não estar claras para o P1, devido à alta frequência de perguntas sobre o funcionamento do jogo. Contudo, os resultados obtidos com o registro do comportamento de solicitar ajuda para executar ações do jogo, e as porcentagens de acertos de emparelhamentos precisos mostram que a usabili-dade proporcionada pelo software não oferecia maiores dificuldades. Ainda que a principal tarefa executada pelos participantes fosse arrastar as peças de dominó, havia outras ações como clicar para acessar os mapas, para escolher os mapas, para escolher as ilhas etc. que não foram registradas. O registro completo do uso do jogo poderia fornecer uma avaliação mais segura das questões referentes à usabilidade.

Também buscou-se avaliar a usabilidade do jogo por meio de observações diretas do comportamento. Avaliações de usabilidade geralmente fazem uso de medidas diretas e indiretas. Medidas diretas, chamadas de indicadores de usabilidade, envolvem o registro da porcentagem de usuários que obtiveram sucesso na tarefa, o tempo necessário para a realização, tempo que o usuário ficou envolvido em atividades produtivas e improdutivas (erros, desvios, loops do sistema etc.) entre outros (^{Cybis et al., 2010}). A avaliação do jogo Korsan foi semelhante ao indicado na literatura de usabilidade, ao registrar as porcentagens de emparelhamentos precisos das peças pelos participantes. As medidas indiretas de relato verbal, comumente utilizadas em testes de usabilidade, são obtidas pela coleta de dados de verbalizações simultâneas e consecutivas. No registro de verbalizações simultâneas, durante o uso do software, são feitas perguntas para que respostas e comentários gerais sejam registrados. A avaliação por verbalizações consecutivas constitui-se de uma entrevista posterior ao uso, na qual o usuário é questionado sobre suas ações para executar as tarefas enquanto assiste a um vídeo de sua interação com o software (Cybis et al., 2010). Embora a avaliação de usabilidade do jogo Korsan se pareça com o registro de verbalizações simultâneas, não foram programadas perguntas para os participantes e o registro foi feito a partir das verbalizações espontâneas. Além disso, foram criadas categorias comportamentais que permitissem a obtenção de resultados quantitativos.

O jogo parece cumprir seus objetivos de ensino e apresentar usabilidade adequada para crianças da faixa etária avaliada. O acréscimo de outros elementos de enredo e estética como a presença do personagem pirata, de baús de tesouro pode produzir maior engajamento dos jogadores durante as partidas. Futuras pesquisas podem incorporar tais elementos, além de buscar refinar as avaliações de engajamento e usabilidade, uma vez que o desenvolvimento de medidas de observação direta do comportamento ainda é incipiente. Nesse estudo, foram programadas atividades concorrentes às partidas com o jogo para compor a avaliação de engajamento. Estudos futuros podem realizar avaliações de preferência antecipadamente para programar tais atividades. Ainda, testes de generalização com problemas em outras formas de apresentação e avaliação de outras habilidades podem ser programados para avaliar a extensão dos efeitos do jogo sobre o comportamento dos jogadores.