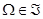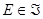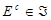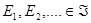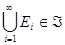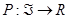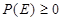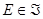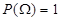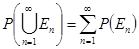2.1 Aspectos contextuales

La probabilidad es una rama de las matemáticas que puede incrementar la comprensión de los individuos sobre los fenómenos aleatorios que se suscitan en la naturaleza o en la sociedad. Es así que la probabilidad se convierte en una herramienta fundamental para desarrollar procesos de inferencia estadística; en este sentido, la estadística se ha consolidado como la ciencia de los datos y un elemento fundamental del método científico experimental (^{Batanero, 2001}). El estudiante de educación pre-universitaria y futuro ciudadano o el profesional en diversas disciplinas, necesita acceder de manera pertinente a estos conocimientos, para afrontar de mejor forma, los retos, desafíos y múltiples interrogantes que se presentan en la actual sociedad globalizada y compleja en la que está presente lo determinista y lo aleatorio.

Aunque la probabilidad tuvo sus orígenes en los juegos de azar y suerte, actualmente se ha consolidado como una rama de las matemáticas con grandes repercusiones y aplicaciones en el campo de la investigación científica, los negocios, la industria, la política, y la vida diaria de la gente (^{Swenson, 1998}; ^{Gómez, 2014}). Por ejemplo, la probabilidad está presente en la interpretación de los resultados asociados a distintos tipos de enfermedades y a sus posibles consecuencias en la vida de las personas y en el medio ambiente, en la predicción del estado del tiempo o del valor de las acciones en el mercado bursátil e incluso en la evaluación del riesgo que a futuro podría tener un determinado negocio. Con la ayuda de modelos probabilísticos los empresarios han tomado mejores decisiones con base en los pronósticos referentes al comportamiento del mercado, se ha logrado estimar un valor esperado para el dólar, proyectar las posibles tarifas para los seguros de vida y contra accidentes, y realizar el control de calidad a los productos de consumo, entre otros. Los profesionales de la medicina se apoyan en la probabilidad para decidir sobre el diagnóstico y tratamiento de sus pacientes, informarlos acerca de los posibles riesgos o de los efectos colaterales producto de las medicaciones (^{Swenson, 1998}).

Los investigadores en el campo de las ciencias naturales o de las ciencias sociales utilizan elementos de la teoría de la probabilidad para diseñar experimentos e interpretar los resultados de su aplicación (^{Gómez, 2014}). Hoy, quizá de manera inconsciente, los ciudadanos son influenciados por la probabilidad cuando creen en los sondeos sobre posibles ganadores en las contiendas políticas, siguen las recomendaciones del meteorólogo sobre el estado del tiempo o cuando compran un boleto de la lotería con la ilusión de ganarla. En cambio, la estadística es considerada un instrumento para el análisis de información y utilizada para soportar procesos de investigación científica en esta sociedad de continuo cambio sustentado en la incertidumbre, el conocimiento, la información, la tecnología y la comunicación. Se considera que la probabilidad se ha de constituir en “una de las doce capacidades matemáticas esenciales que los futuros ciudadanos necesitarán en el siglo XXI” (^{NCSM, 1989}).

Debido a que cada día, con mayor fuerza la probabilidad está influenciando las actividades de nuestra vida cotidiana y se ha constituido en un elemento fundamental del método científico, es pertinente desarrollar contenidos de probabilidad dentro del currículo de matemáticas desde el nivel de la educación primaria y secundaria, hasta el universitario, de manera que promueva la consolidación de una cultura probabilística y la construcción del conocimiento científico (^{Burbano, 2013}). La cultura probabilística hace referencia a la capacidad que tiene una persona para “comprender los enunciados de probabilidad en el contexto de apuestas, votaciones, o inversiones en la bolsa” (^{Gal, 1995}) y diversos fenómenos aleatorios.

En nuestro país, de manera formal, el MEN sugirió el estudio de tópicos asociados con la probabilidad como parte del currículo de matemáticas mediante los LC a partir del año 1998; al igual que en otros países, su inclusión se debe al reconocimiento del trascendental papel en el desarrollo de la sociedad moderna al posibilitar el análisis de información y toma de decisiones en situaciones de incertidumbre. Igualmente, la inclusión de temas relacionados con la probabilidad en el currículo escolar también se constituye en un enorme desafío para Colombia y los demás países, en tanto que el recurso humano calificado (profesores) es aún limitado (^{Zapata, 2011}).

La UPTC a través del Acuerdo 021 de 1993, establece que sus profesores han de cumplir funciones de academia, investigación y extensión (^{Burbano, 2013}). En correspondencia con las dos últimas funciones, desde el “Grupo de investigación Interdisciplinario en Ciencias” (GICI) de esta universidad, se ha propuesto contribuir con el mejoramiento de la educación estocástica del nivel pre-universitario; por eso, en principio, se pretende indagar sobre un “modelo de conocimiento del profesor” que oriente el proceso de enseñar la probabilidad en el entorno local, para luego detectar potencialidades y debilidades en el profesor en ejercicio a fin de apoyarlo con conocimiento probabilístico y algunas recomendaciones de tipo didáctico que contribuyan con la mejora de su práctica pedagógica (^{Gómez, 2014}).

El presente trabajo se focaliza especialmente en el campo de la Didáctica de la probabilidad enmarcado en el ámbito de la Educación estadística; trata de extrapolar la teoría del Conocimiento Base para la Enseñanza, CBE, hacia la enseñanza de la probabilidad en el nivel pre-universitario y destaca la importancia del paradigma de Shulman en la generación de otros modelos destinados a la enseñanza de las matemáticas y la estadística; sin embargo, la revisión de la literatura permite establecer que aún no se ha consolidado un modelo con características específicas para enseñar probabilidad.

2.2 Marco conceptual

La probabilidad se puede conceptualizar como “la medida de la posibilidad de que un evento ocurra” (^{Blanco, 2004}; ^{Valdivieso, 2010}). A lo largo de la historia, se han generado diversas definiciones sobre el término probabilidad, entre ellas: la intuitiva, clásica, frecuencial, subjetiva y axiomática (^{Gómez, 2014}; ^{Burbano, 2015}). El concepto de probabilidad es un elemento fundamental para que el docente pueda enseñar diversos tópicos relacionados con la comprensión de los fenómenos aleatorios; desde un punto de vista didáctico, es conveniente que el profesor inicie a sus estudiantes con las ideas intuitivas durante los primeros años de escolaridad y prosiga de forma gradual con las concepciones clásica y frecuencial con el fin de hacer una aproximación hacia la axiomática en los últimos grados de la educación media.

Las ideas intuitivas sobre el azar se manifiestan en los niños y en las personas quienes aún no han recibido formación en el tema de probabilidad por medio de la utilización frecuente de términos y expresiones coloquiales como: presumible, posible, previsible y plausible en el propósito de cuantificar los sucesos inciertos y de expresar su grado personal de creencia en éstos (^{Batanero & Sánchez, 2005}). Esta creencia resulta útil para empezar a cuantificar la ocurrencia de sucesos aleatorios, al considerarlos nada, poco o muy probables.

En la concepción clásica también denominada laplaciana, la “probabilidad de un evento que puede ocurrir solamente en un número finito de formas, se define como el cociente entre el número de casos favorables y el número de casos posibles, siempre y cuando todos los resultados posibles sean igualmente probables” (^{Laplace, 1812}); es decir, que tengan la misma verosimilitud (^{Alexander & Kelly, 1999}). Este constructo ha presentado un limitado campo de aplicación porque exige contar con un conjunto finito de resultados posibles verosímiles; adicionalmente, la definición es circular ya que el concepto de equiprobabilidad (resultados posibles igualmente probables) requiere una aplicación previa del propio concepto de probabilidad.

En la concepción frecuencial, si un proceso se puede repetir en idénticas condiciones un número grande de veces “n” y si algún evento de interés en ese proceso ocurre “m” veces, la frecuencia relativa obtenida de dividir m entre n es aproximadamente la probabilidad del evento de interés. Este concepto fue propuesto por Mises (1928) en la búsqueda de una axiomatización para la teoría de la probabilidad. En general, la concepción frecuencial es útil para estimar probabilidades en los casos que se tengan grandes cantidades de repeticiones. En este contexto, puede ser útil la implementación de procesos de simulación para la estimación de probabilidades.

Desde una concepción subjetivista, la probabilidad es el grado de creencia personal sobre la ocurrencia de un fenómeno que se considera impredecible bajo un conjunto de hipótesis establecido. El valor de la probabilidad asignado depende de la información previa que posea el individuo sobre el evento de interés. Dos personas pueden asignar probabilidades distintas para un mismo suceso. Este concepto fue impulsado por el matemático Savage en la década de los años 50 en el siglo XX. Hoy, se utiliza para asignar probabilidades a priori en estadística bayesiana.

Desde una concepción axiomática, la probabilidad es un concepto formulado mediante un sistema de axiomas, definiciones y teoremas; estos últimos, son proposiciones demostrables que indican la forma como una probabilidad se obtiene a partir de otras (^{Díaz, Batanero & Cañizares, 1996}). La axiomática es con frecuencia adoptada por las instituciones educativas con poca reflexión sobre sus alcances y limitaciones en los procesos de aprendizaje de los estudiantes (^{Gómez, 2014}).

De manera sucinta, la teoría axiomática de la probabilidad establecida por Kolmogórov en 1933, involucra los siguientes elementos asociados con el concepto de probabilidad (^{Burbano, 2015}): el conjunto de todos los resultados posibles de un experimento aleatorio denominado espacio muestral 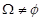en el que se ha definido una 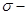álgebra 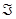sobre o familia de subconjuntos de que satisface los siguientes axiomas:

i)

ii) Si entonces

iii) Si entonces

A la pareja 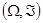se le denomina espacio medible y a los elementos de la familia 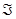se les llama eventos.

Ahora, si 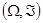es un espacio muestral medible, una función de conjunto,

Tal que:

i) para todo

ii)

iii) Si 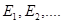es una sucesión de eventos en 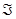tales que 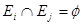para todo 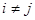entonces

entonces la función 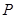se llama una medida de probabilidad sobre el espacio muestral y la tripleta ordenada 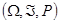se le denomina un espacio de probabilidad sobre .

2.3 Marco teórico del Conocimiento Base para la Enseñanza

La determinación de los conocimientos requeridos por el profesor para la enseñanza de la probabilidad en los diferentes niveles escolares, es una de las problemáticas que ha generado gran interés en investigadores tanto a nivel internacional como nacional (^{Burbano, 2013}; ^{Gómez, 2014}). Paradigmas de investigación focalizados en el “conocimiento pedagógico” (^{Moore, 1974}), “Conocimiento Base para la Enseñanza” (^{Shulman, 1986}, ¹⁹⁸⁷) y “Conocimiento matemático para la enseñanza” (^{Ball, Thames & Phelps, 2008}), aportan destacados avances investigativos. Los paradigmas de Shulman, los de Ball y colaboradores, junto a los planteamientos de ^{Taylor y Bogdan (1987)}, ^{Rodríguez, Gil y García (1999)}, sobre investigación cualitativa y ^{Stake (1998)} y ^{Simons (2011)} acerca de los estudios de caso generan potenciales metodologías encaminadas a investigar procesos de enseñanza y aprendizaje de diversos tópicos en estocástica y de matemáticas en general (^{Gómez, 2014}).

En lo que hace referencia a la enseñanza de las matemáticas y de la estocástica, durante bastante tiempo se ha pensado de forma equivocada que es “suficiente con poseer un conocimiento disciplinar profundo y ciertas habilidades pedagógicas para enseñar estas materias” (^{Burbano, 2013}). En la última década, se ha reconocido que la problemática presenta mayor complejidad y puede atribuirse a aspectos “epistemológicos, cognitivos, didácticos y del contexto” (^{Salinas & Alanís, 2009}; ^{Burbano, 2013}). En lo que concierne al proceso de enseñar tópicos relacionados con la probabilidad, algunos problemas radican en la base epistemológica y cognitiva generada por la precaria formación en probabilidad recibida por los profesores que la enseñan (^{Shaughnessy, 1992}; ^{Burbano, 2013}; ^{Gómez, 2014}); otros pueden deberse a factores de carácter pedagógico y didáctico generados por las concepciones de los docentes acerca de probabilidad o con las estrategias implementadas en el aula. En educación estocástica, no resulta pertinente la transferencia de “algunos principios generales válidos para la geometría, la aritmética u otras ramas de las matemáticas” (^{Batanero, Godino & Roa, 2004}; ^{Burbano, 2013}). Tampoco se exceptúan factores relacionados con preconceptos, concepciones erradas, maneras de aprender de los estudiantes y los recursos didácticos disponibles (^{Burbano, 2013}; ^{Gómez, 2014}). Con respecto al “currículo”, generalmente, los planes de estudio presentan poco contenido de probabilidad (^{Arias & Cardona, 2008}).

Un marco teórico que posibilita la investigación de dicha problemática desde la perspectiva del “conocimiento profesional del profesor” es el denominado Conocimiento Base para la Enseñanza (CBE) propuesto por ^{Shulman en 1987}, el CBE está constituido por siete categorías: “conocimiento del contenido de la disciplina, conocimiento didáctico general, conocimiento del currículo, conocimiento pedagógico del contenido, conocimiento de los estudiantes y sus características, conocimiento de los contextos educacionales y conocimiento de los objetivos, las finalidades y los valores educacionales, y de sus fundamentos filosóficos e históricos” (Shulman, 1987). En concordancia con este autor, ^{Burbano y Valdivieso (2014)} han extrapolado esas categorías para la “enseñanza de la probabilidad” en el nivel pre-universitario y han enfatizado la necesidad de que el docente deba poseer una base de conocimientos sólida para orientar el “aprendizaje de la estocástica y en particular para enseñar la probabilidad”, esa base se constituye por las categorías:

i) Conocimiento del contenido disciplinar. En el caso de probabilidad, significa que el docente ha de acreditar conocimientos suficientes acerca de los tópicos relacionados con esta rama de las matemáticas, en consonancia con los estándares curriculares establecidos por el MEN; de tal forma que logre orientar a sus alumnos en su “aprendizaje” de acuerdo a las concepciones clásica, frecuencial, subjetiva o axiomática de probabilidad (^{Burbano & Valdivieso, 2014}).

ii) Conocimiento didáctico general. Este involucra entre otros: principios y estrategias para organizar e interactuar durante la clase de probabilidad; capacidad y habilidad para enseñar determinados tópicos asociados con la probabilidad pero acorde al nivel escolar en el cual se encuentre el estudiante y mediante estrategias de aprendizaje usadas de manera diferenciada; aprovisionamiento de una amplia gama de actividades y de “representaciones destinadas a la enseñanza de la probabilidad” (^{Burbano & Valdivieso, 2014}).

iii) Conocimiento del currículo. Involucra un conocimiento y un dominio adecuado de los materiales y programas de curso, los cuales han de servir como instrumentos para: el oficio docente, dar gradualidad a los contenidos y transitar desde lo intuitivo hacia lo axiomático en el caso de probabilidad; con apoyo de materiales como dados, ruletas, o software es posible que el docente motive al estudiante para que realice simulaciones (^{Burbano, 2013}). Lo anterior, guarda relación con los Lineamientos Curriculares (^{MEN, 1998}), en los cuales se indica que el pensamiento aleatorio, mediante contenidos de probabilidad ha de estar “imbuido de un espíritu de exploración y de investigación tanto por parte de los profesores como de los alumnos” (^{Gómez, 2014}).

iv) Conocimiento pedagógico del contenido (PCK, Pedagogical Content Knowledge) Identifica los cuerpos de conocimiento distintivos para desarrollar el proceso de enseñar, “representa la mezcla entre materia y didáctica por la que se llega a la comprensión de cómo determinados temas y problemas se organizan, se representan y se adaptan a los diversos intereses y capacidades de los alumnos y se exponen para su enseñanza” (^{Shulman, 1986}). El PCK puede corresponder a “las formas más útiles de representación del contenido, […] las más poderosas analogías, ilustraciones, ejemplos, explicaciones y demostraciones”, de manera breve, las formas de representación y formulación de la materia que la hagan comprensible a otros (^{Shulman, 1987}, ^{Burbano, 2015}).

v) Conocimientos sobre los estudiantes y sus características. En principio, el profesor ha de realizar un diagnóstico de las maneras de aprender de sus estudiantes, sus motivaciones e intereses o sus estilos de aprendizaje (^{Burbano, 2013}); por ejemplo, la simulación puede constituirse en un elemento extrínseco de motivación para el aprendizaje del tema de probabilidad desde el enfoque frecuencial (^{Burbano y Valdivieso, 2014}; ^{Gómez, 2014}). El docente ha de poseer conocimiento del proceso evolutivo del estudiante en lo que respecta al razonamiento probabilístico, en concordancia con ^{Piaget & Inhelder (1951)} el alumno evoluciona a través de tres etapas: preoperatoria, operaciones concretas y operaciones formales; por su parte ^{Fischbein (1975)} señala que “los niños tienen ideas correctas parcialmente formadas sobre los conceptos probabilísticos” y la intuición tiene un efecto particular para mejorar esas ideas (^{Batanero, 2001}; ^2001a).

vi) Conocimiento de los contextos educacionales. En concordancia con ^{Shulman (1987)}, este tipo de conocimiento abarca desde la dinámica del grupo o de la clase hasta los aspectos culturales de la comunidad escolar. En estas circunstancias, el docente ha de incrementar gradualmente su conocimiento de tales contextos con el fin de que el tratamiento de los fenómenos aleatorios tenga sentido para los estudiantes, por ejemplo, ha de ser consciente de que el uso de materiales manipulables y el software de simulación para trabajar probabilidad pueden tener un determinado impacto en correspondencia con “el contexto donde se utilicen” (^{Burbano y Valdivieso, 2013}), sea en la clase, el aula de informática, los juegos de azar o en la vida cotidiana.

vii) Conocimiento de objetivos, finalidades y valores educacionales, y de sus fundamentos filosóficos e históricos (^{Shulman, 1987}). En esta categoría, el docente ha de identificar de forma clara los objetivos, estándares y derechos básicos de aprendizaje propuestos por el MEN y la institución educativa respecto a probabilidad; además, es conveniente abordarla apoyándose en aspectos de tipo histórico, epistémico o filosófico asociados con los conceptos probabilísticos (^{Burbano, 2013}).

En lo concerniente al “conocimiento matemático” requerido por el docente para enseñar el tema de probabilidad, ^{Ball, Thames & Phelps (2008)}, han realizado una exhaustiva revisión acerca de los “conceptos” desarrollados en ^{Shulman (1986}, ¹⁹⁸⁷) en los que examinaron diversas formas para su operacionalización en el ámbito de la “educación matemática”; Ball et al., propusieron el concepto de “Conocimiento Matemático para la Enseñanza” (MKT, Mathematical Knowledge for Teaching), este puede entenderse como “aquel conocimiento matemático que usa el profesor en el aula para producir instrucción y crecimiento en el alumno”; asimismo, crearon un modelo conformado por el conocimiento del contenido matemático (MCK) y el PCK. En esta misma dirección, ^{Hill, Ball & Schilling (2008)} señalan que el MCK contempla el Conocimiento Común del Contenido, el Conocimiento Especializado del Contenido y el Conocimiento en el Horizonte Matemático.

El PCK, direccionado hacia el área de las matemáticas, en el sentido de Shulman, puede entenderse como “una forma particular de comprensión profesional del profesor”, en la cual se conjugan el MKC con didácticas específicas apropiadas (ej. representaciones pertinentes del contenido) con el propósito de hacer enseñable un tópico específico al estudiante (^{Burbano, 2013}). De acuerdo con ^{Hill et al. (2008)}, en lo referente al PCK en matemáticas se pueden establecer tres componentes: el Conocimiento del Contenido y del Estudiante, el Conocimiento del Contenido y la Enseñanza y el Conocimiento del Contenido y del Currículo.

Finalmente, si la probabilidad es conceptualizada como la medida numérica de la posibilidad de que un evento ocurra, el profesor ha de poseer un MCK específico para enseñar el tema de probabilidad que puede incluir: i) un conocimiento común del contenido referente a la probabilidad, ii) un conocimiento especializado, y iii) un conocimiento en el horizonte matemático (^{Gómez, 2014}; ^{Burbano, 2015}).

3.1 Modelos de conocimiento del profesor

En concordancia con ^{Batanero y Díaz (2012)}, el proceso formativo de los docentes de matemáticas, con frecuencia, carece de un curso específico destinado a recoger aspectos asociados con la didáctica de la probabilidad, tal vez porque el “currículo de probabilidad” apenas se empieza a implementar en la educación pre-universitaria, aunque organismos internacionales y nacionales han sugerido su implementación por más de treinta años. A continuación se presentan algunos modelos teóricos que de forma sucinta se relacionan con el “conocimiento profesional del profesor” de matemáticas o de estadística, los cuales tienen su génesis en la teoría de Shulman; no obstante, para el tema de probabilidad, aún no se ha generado un modelo específico.

En la actualidad, los estudios relacionados con el conocimiento profesional del profesor de matemáticas son numerosos y han generado diversos modelos, propuestos en los últimos veinte años; varios de éstos fueron compilados por ^{Wood (2008)}, y sus raíces se remontan a ^{Shulman (1986}, ¹⁹⁸⁷). Los que tienen que ver con el ámbito de la educación estadística, fueron recogidos por la International Comisión Mathematical Instruction (ICMI) y la International Asociation for Statistical Education (IASE), las cuales describen de forma detallada algunos modelos para la enseñanza de la estadística (^{Gómez, 2014}; ^{Burbano, 2015}); sin embargo, en referencia a la enseñanza de la probabilidad en los niveles de la educación pre-universitaria, aún no se ha estructurado un modelo con categorías y dimensiones específicas; en este sentido, los trabajos de ^{Jones, Langrall, Thornton y Mogill (1997)}, junto con el de ^{Even y Kvatinsky (2010)}, proporcionan aproximaciones iniciales.

Desde 1986, Shulman ha sido reconocido por la comunidad científica como pionero en efectuar estudios sobre los conocimientos requeridos por el docente para enseñar diversas materias, en particular para orientar el proceso de aprender matemáticas. Inicialmente, este autor propone tres tipos de conocimiento, a saber: conocimiento del contenido a enseñar, conocimiento pedagógico y conocimiento didáctico del contenido, estas categorías de conocimiento se constituyen en una primera respuesta a la necesidad de que los profesores aprendan y manejen otros tipos de conocimientos para desarrollar una enseñanza eficaz. Con base en la tercera categoría de conocimiento, se han generado diversos modelos destinados a enseñar ciencias, matemáticas, estadística u otras ramas del conocimiento; entre ellos: el modelo de Ball, el modelo de Godino, el modelo de Schoenfeld y Kilpatrick, y el modelo del conocimiento didáctico matemático, por citar algunos (^{Gómez, 2014}).

Actualmente, refiriéndose al conocimiento didáctico del contenido, el propio Shulman reconoce que se siente como el padre biológico de un bebé que vio crecer en su infancia y luego fue dado en adopción cuando tenía cinco años de edad. Durante los años subsiguientes, el joven fue criado por muchos padres y ha jugado con muchos compañeros. Ahora que ha sobrevivido y alcanzado la adultez emergente, un gran número de investigadores sabe mucho más acerca del PCK porque han estado viviendo con él, su crecimiento, revisión y aplicación de ese conjunto de ideas serias, en investigación y en el trabajo pedagógico (^{Shulman, 2015}, p. 3).

^{Godino (2009)}, propuso un modelo en el marco del Enfoque Onto-Semiótico (EOS) con el objetivo de identificar limitaciones existentes en otros modelos y de superarlas al refinar las categorías expuestas en el MKT principalmente, este fue estructurado con seis dimensiones y cuatro facetas destinadas al análisis del conocimiento profesoral necesario para enseñar matemáticas. Las seis dimensiones son: epistémica, cognitiva, afectiva, interaccional, mediacional, y ecológica. Las cuatro facetas que se incluyen en el modelo son: prácticas matemáticas y didácticas, configuraciones de objetos y procesos, normas y metanormas, e idoneidad.

El modelo de ^{Schoenfeld y Kilpatrick (2008)}, tiene como propósito incluir la llamada “teoría del conocimiento experto”, se constituye por siete dimensiones acerca de los “conocimientos y competencias” requeridas por el docente para enseñar matemáticas, a saber: i) conocimiento amplio y profundo de las matemáticas escolares, ii) conocimiento sobre las maneras de pensar de los estudiantes, iii) conocimiento de las maneras de aprender de los estudiantes, iv) diseño experto y gestión de entornos de aprendizaje acordes con lo actual, v) desarrollo de normas dentro del aula, vi) construcción de relaciones que favorezcan el aprendizaje al articular los contenidos y sus representaciones, y vii) reflexión sobre su quehacer docente a fin de mejorarlo continuamente.

El modelo del conocimiento didáctico matemático (CDM) propuesto por ^{Pino-Fan (2013)}, es el resultado de la fusión del MKT de Ball y del PCK de Shulman; este modelo contempla tres categorías globales: i) Conocimiento común del contenido, ii) Conocimiento ampliado del contenido, y iii) Conocimiento especializado; las cuales guardan cierta similitud con las categorías del modelo de Ball pero que recogen aspectos adicionales y la reestructuración de otros.

Los modelos mencionados incluyen componentes del conocimiento profesional docente requeridos para mejorar la enseñanza de las matemáticas, todos ellos con fuertes raíces en el paradigma de Shulman aunque estructurados desde diversas perspectivas; Shulman empieza por señalar los conocimientos requeridos (CBE) por el docente para ejercer adecuadamente su profesión y hace énfasis en el PCK como un elemento clave para potenciar en el maestro una mejora en el proceso de enseñar; Ball y su equipo operacionalizan la idea de Shulman y le inyectan algunos matices propios con el fin de valorar el conocimiento del profesor; Schoenfeld y Kilpatrick promueven las relaciones interpersonales en el salón de clases y conciben los procesos de enseñanza y de aprendizaje como interactuantes, con matices humanos y sociales asociados a los actores; luego, ^{Godino (2009)}, hace una amalgama de los tres modelos tendiente a entender lo complejo de tales procesos y ampliar las distintas herramientas existentes para realizar un “análisis didáctico”, finalmente, Pino-Fan propone el CDM.

Las categorías presentes en el MKT de Ball son un tanto difusas puesto que los diversos tipos de conocimientos allí presentes dependen en buena medida del contexto. En tal sentido, se ha reconocido que “no siempre es fácil distinguir dònde una de nuestras categorías se separa de otra, y esto afecta a la precisión de nuestras definiciones o su falta de precisión” (^{Ball, et al., 2008}). En el modelo de Schoenfeld y Kilpatrick, el estudiante desempeña un rol activo y participativo ya que las interacciones juegan un papel fundamental en la comunidad escolar; no obstante, esta característica se recoge en gran medida en el CBE de Shulman en la categoría del PCK direccionada hacia el conocimiento de las formas de aprender del alumno (^{Burbano, 2015}).

Por otra parte, en el campo de la educación estadística son pocos los modelos que se han propuesto para potenciar su enseñanza; no obstante, los que se han generado tienen fuertes nexos con el modelo de Shulman, entre ellos: el de ^{Godino, Batanero y Flores (1999)}, el de ^{Burgess (2008}, 2011), el modelo de ^{Lee y Hollebrands (2008}, 2011), y el modelo de ^{Garfield y Ben-Zvi (2008)}, entre otros.

El modelo de ^{Godino, Batanero y Flores (1999)} tiene como propósito describir los conocimientos estocásticos y didácticos del profesor para promover el aprendizaje activo, está conformado por cuatro componentes: i) la reflexión epistemológica sobre el conocimiento estocástico; ii) el análisis de las transformaciones de los objetos estocásticos para adaptarlos a un nivel educativo específico; iii) el conocimiento de dificultades, obstáculos y errores estudiantiles para aprender y de estrategias usadas en la resolución de problemas; y iv) la ejemplificación de situaciones didácticas, métodos de enseñanza usados en temas particulares y recursos didácticos apropiados (^{Godino, et al., 1999}; ^{Gómez, 2014}). Este modelo fue refinado por ^{Batanero, Godino y Roa (2004)}, resultando un modelo constituido por seis componentes: reflexión epistemológica, experiencia, capacidad crítica, estrategias para resolver tareas, desarrollo de instrumentos de evaluación y uso de buenos ejemplos.

En el modelo de ^{Burgess (2008}, ²⁰¹¹), el objetivo fue trasferir el MKT hacia la enseñanza de la estadística, el modelo fue estructurado a partir del MKT y un modelo de descripción del pensamiento estadístico propuesto por ^{Wild y Pfannkuch (1999)}; este modelo se constituye por cuatro componentes, con el fin de enseñar estadística: i) el ciclo de investigación, compuesto por las fases a seguir cuando se realiza una investigación de corte estadístico, ii) el ciclo interrogativo, usado en el trabajo estadístico frecuente, iii) las disposiciones actitudinales, las cuales son frecuentes en un estadístico, p.ej.: creatividad, perseverancia y escepticismo, y iv) las categorías asociadas con “modos fundamentales de razonamiento” en estadística.

El modelo de ^{Lee y Hollebrands (2008}, ²⁰¹¹), tiene como propósito integrar el conocimiento del docente de matemáticas y ciencias referido al contenido, la pedagogía y la tecnología; este modelo es también denominado de “conocimiento estadístico pedagógico tecnológico de los profesores” (TPSK). Este modelo resultó de una adaptación del enfoque de ^{Niess (2005)}, usado en estadística. En la elaboración de tal modelo se usan cuatro elementos de la teoría de Shulman, obteniéndose el modelo TPCK conformado por las siguientes cuatro categorías: i) concepciones sobre el significado de enseñar un tema específico mediante tecnología, ii) conocimiento de estrategias y representaciones a fin de enseñar tópicos específicos a través de tecnología, iii) conocimiento referido al razonamiento, comprensión y aprendizaje de los alumnos por medio de la tecnología, y iv) conocimiento sobre los materiales y el currículo de manera que integren la tecnología con el aprendizaje estudiantil.

El modelo de ^{Garfield y Ben-Zvi (2008)}, tiene como objetivo promover el razonamiento estadístico y el desarrollo de competencias en futuros profesores, incluyendo cinco, las que se han de desarrollar durante el proceso de formación docente: i) ideas estadísticas fundamentales; ii) utilización de datos recogidos de entornos reales; iii) realización de actividades en el salón de clase integrando la tecnología; iv) manejo del discurso durante la clase, y v) utilización de metodologías alternas de evaluación del aprendizaje. Es conveniente señalar que estas competencias poco se relacionan con las mencionadas en la literatura habitual sobre formación de profesores; sin embargo, podrían constituirse en aspectos a tener en cuenta para la formación estocástica, tanto de profesores como de estudiantes (^{Burbano, 2015}).

Los modelos mencionados son potencialmente útiles en la enseñanza de tópicos de matemáticas y de estadística, respectivamente; no obstante, sus estructuras y dimensiones podrían utilizarse en la enseñanza de la probabilidad y el desarrollo del pensamiento aleatorio; conviene que el futuro profesor y el profesor en ejercicio los asimile y los ponga en práctica para luego valorarlos; asimismo, ha de documentar y acrecentar sus conocimientos a través de la revisión de investigaciones como las que se mencionan en el siguiente apartado.

3.2 Un breve panorama investigativo asociado con la didáctica de la probabilidad

Aunque diversos trabajos de investigación han realizado aportes significativos y proporcionan más claridad sobre el “conocimiento profesional” que necesitan los docentes para enseñar determinadas materias como química, biología, ciencias, matemáticas (^{Pinto, 2010}), la investigación acerca de conocimientos pedagógicos, dominio del contenido probabilístico en el profesor y conocimiento sobre las formas de aprender del estudiante, es todavía limitada (^{Burbano, 2015}); esto puede atribuirse a que la introducción de la probabilidad en la educación pre-universitaria, es “relativamente nueva” (^{Jones, Langrall & Mooney, 2007}; ^{Gómez, 2014}). Por esto se requieren formas alternativas que permitan observar de manera más directa los conocimientos que el maestro pone en juego cuando enseña probabilidad para potenciar en sus estudiantes la comprensión de “conceptos probabilísticos” y el desarrollo del pensamiento aleatorio (^{Vásquez, 2014}).

La revisión de la literatura en el contexto nacional e internacional ha permitido establecer que, desde mediados del siglo XX hasta los años 80, se desarrollaron investigaciones tendientes a estudiar la cognición sobre probabilidad, la manera como los individuos aprenden, piensan y toman decisiones en situaciones aleatorias (^{Piaget & Inhelder, 1951}), desarrollan intuiciones sobre “el azar y la probabilidad” (Fischbein, 1975), a indagar sobre heurísticas, concepciones erróneas, sesgos en el desarrollo cognitivo de conceptos probabilísticos y comprender más sobre “creencias, intuiciones y razonamiento probabilístico”; asimismo, a diagnosticarlos en personas adultas y estudiantes de distintos niveles escolares (^{Kahneman & Tversky, 1972}).

El futuro profesor y el profesor en ejercicio, han de aprovechar dichas investigaciones para documentarse y acrecentar sus conocimientos con el fin de mejorar sus procesos de enseñanza, un docente sin una preparación consciente y pertinente, puede depender de sus “concepciones, creencias e intuiciones y mostrar razonamientos y sesgos” parecidos a los encontrados en estudios sobre la cognición en torno a la probabilidad mencionados anteriormente (^{Burbano, 2015}).

Entre los años 80 y 90, la investigación en “enseñanza de la probabilidad” se focalizó en la “resolución de problemas” con los trabajos de ^{Green (1983)}, ^{Fischbein y Gazit (1984)} y ^{Shaughnessy (1992)}, entre otros. La inclusión oficial de la probabilidad como parte del “currículo escolar de matemáticas” en los años 90 del siglo XX (^{NCTM, 1989}) generó la necesidad de que los docentes adquirieran el “conocimiento del contenido probabilístico” y desarrollen prácticas de aula sobre su enseñanza. Sin embargo, el avance logrado en esta dirección ha sido demasiado lento y apenas se empieza a desarrollar una enseñanza centrada en enfoques conceptuales de tal manera que se generen actividades docentes que incluyan la experimentación aleatoria y proporcionen al estudiantado una “experiencia probabilística desde su infancia”, como lo sugieren el MEN y algunos organismos internacionales (^{NCTM, 2000}; ^{Gómez, 2014}; ^{Burbano, 2015}).

Posteriormente, los investigadores se focalizaron en fortalecer la apropiación de conceptos probabilísticos y el conocimiento disciplinar en probabilidad; asimismo, crece el interés por buscar formas más eficientes de comprender los fenómenos aleatorios y diseñar propuestas sobre qué y cómo enseñar tópicos de probabilidad en la educación pre-universitaria; en esta dirección, se pueden mencionar los trabajos de ^{Serrano (1996)}, ^{Stohl (2005)}, ^{Jones, et al., (2007)}, Godino, et al., (1987, 2008), ^{Arias y Cardona (2008)}, ^{Zapata (2011)}, solo por citar algunos. Específicamente, sobre “enseñanza de la probabilidad” desde el enfoque teórico del PCK se puede mencionar el trabajo investigativo desarrollado por ^{Swenson (1998)}, quien hizo un estudio de caso con docentes de matemáticas de secundaria en los Estados Unidos, con la intención de observar y valorar su PCK cuando realizaban su práctica en el aula. Por su parte, ^{Burbano (2015)} realiza un trabajo focalizado en investigar sobre el PCK de dos profesores que enseñan el concepto de probabilidad a estudiantes de la educación media colombiana; ^{Molina (2016)}, desarrolla un trabajo focalizado en el PCK del tutor de educación a distancia cuando enseña algunas “medidas de tendencia central” en cursos de pregrado.

Desde el Enfoque Onto-Semiótico, se han hecho trabajos alusivos a enseñar tópicos de probabilidad en primaria, tales como: “Evaluación del conocimiento de los futuros profesores sobre probabilidad” (^{Mohamed, 2012}), “Evaluación y desarrollo del conocimiento matemático para la enseñanza de la probabilidad en futuros profesores de educación primaria” (^{Gómez, 2014}), “Evaluación de los conocimientos didáctico-matemáticos para la enseñanza de la probabilidad de los profesores de educación primaria en activo” (^{Vásquez, 2014}), entre otros. Lo anterior indica que este campo investigativo aún está abierto.