2.1 Referentes teóricos

La investigación teóricamente se fundamenta en tres constructos: Pensamiento Matemático Variacional, el Uso de las Tecnologías de la Información y la Comunicación, TIC, y la Secuencia Didáctica.

Para el pensamiento variacional se consideraron los Lineamientos Curriculares propuestos por el Ministerio de Educación Nacional, MEN (1998), donde se definen las características propias del pensamiento variacional, como: la capacidad que posee el estudiante para: identificar situaciones de variación y cambio, explicar su representación gráfica, analizar las tendencias de variación, pronosticar resultados a partir de patrones, medir las variaciones y modelarlas matemáticamente a partir de la covariación. En ese orden de ideas se hace necesario estructurar actividades de aprendizaje que permitan alcanzar un desarrollo completo de cada una de estas características por parte del estudiante (^{Carlson et al., 2003}).

Independientemente de la clase, del nivel o del área, los profesores permanentemente se ven abocados al reto de centrar la atención de sus estudiantes (^{Aldana-Bermúdez & López-Mesa, 2016}; ^{Bernal-Pinzón, 2017}). Curiosamente, en la actualidad existe una gran variedad de medios audiovisuales que son usados por los estudiantes y que escasamente se adaptan y usan en las aulas de clase, con el fin de mediar en el proceso de enseñanza aprendizaje (^{Buitrago-Guzmán, 2014}; ^{Gutiérrez-Rodríguez, 2018}).

Las TIC son parte activa de la sociedad actual y cada vez se hace más importante su utilización, de modo que la educación que se brinda no puede estar ajena a esta realidad. Además, son un recurso para que los estudiantes aprendan matemáticas y su uso en el aula debe estar sustentado en una metodología que facilite el proceso de aprendizaje de los estudiantes (^{Real-Pérez, 2013}; ^{Barrera-Mesa, Fernández-Morales & Duarte, 2017}). En este sentido, es imperativo evitar el uso domesticado de nuevas tecnologías, buscando crear nuevos problemas y actividades investigativas (^{Borba, Scucuglia & Gadanidis, 2014}).

En esta perspectiva, las TIC hacen su aparición en forma de una potente herramienta como mediadoras en el panorama educativo (^{Quiroga-Parra, Torrent-Sellens & Murcia-Zorrilla, 2017}). A pesar de lo anterior, algunos estudios sugieren a las TIC como un obstáculo al momento de hacerlas parte del proceso educativo, en especial cuando los docentes no están capacitados en su uso (^{García-Amaya, Fernández-Morales & Duarte, 2017}). Por el contrario, otros estudios sugieren que su uso en el aula representa un importante beneficio en el alcance de aprendizajes significativos, donde además se logra en los estudiantes un mayor grado de motivación por aprender, y una renovada actitud crítica, que se refleja en un cambio de concepciones y prácticas al interior del aula (^{Valencia-Serrano & Caicedo- Tamayo, 2017}; ^{Avella-Ibáñez, Sandoval-Valero & Montañez-Torres, 2017}).

En su caso, ^{Villa-Ochoa y Ruiz (2010)} van más allá del constructo TIC. Estos autores hablan de “un colectivo pensante de humanos-con-medios”, el cual se fundamenta en dos ideas principales: la primera es que “la cognición no es un trabajo individual sino más bien de naturaleza colectiva” y, la segunda, que la construcción del conocimiento incluye “herramientas, dispositivos, artefactos y medios”.

Por su parte, ^{Borba (2002)} sugiere que “la producción del conocimiento se logra a partir de un colectivo compuesto por humanos y no humanos”. En particular, este autor enfatiza en “el papel que los medios tienen, como actores no humanos, en moldear las posibilidades que tienen esos colectivos de construir conocimiento”. Igualmente, ^{Claro (2010)} sugiere que las TIC impactan la motivación y concentración del estudiante en el proceso de enseñanza-aprendizaje, por las posibilidades de interacción y animación a la hora de presentar los conceptos y las actividades, lo cual permite aumentar la permanencia de los estudiantes en el aula.

En el presente estudio, la mediación con las TIC pretende fortalecer el desarrollo del pensamiento variacional en los estudiantes de grado noveno, teniendo en cuenta los planteamientos del MEN (2004), donde se recomienda que los estudiantes hagan uso efectivo de los sistemas de representación. Esto permite aprovechar la opción de graficación que poseen las tabletas con la aplicación Geogebra, facilitando el análisis de problemas variacionales. Sin embargo, en el aula existen otros usos con las TIC, que también favorecen el aprendizaje, como lo expresaron ^{Jaramillo, Castañeda y Pimienta (2009)}, identificándolos según su utilidad, a saber: la administración del curso; la elaboración de material de apoyo; la presentación de información en el aula, cuando se socializan los temas con recursos audiovisuales; la búsqueda de información, cuando se consulta información vía internet; la publicación de información, cuando se sube información a sitios virtuales como blogs; la evaluación, cuando se realiza en plataformas interactivas como Moodle; la lectura y ejercitación, cuando las presentaciones proponen problemas de retroalimentación o de contexto; las simulaciones, cuando se trabaja en la construcción de portafolios; desarrollo de productos digitales; interacción virtual, se da cuando existe un diálogo en foros, chat y/o correo electrónico.

El otro aspecto considerado en este estudio son las secuencias didácticas, las cuales fueron diseñadas según los lineamientos de ^{Díaz-Barriga (2013)}, donde considera que “las secuencias constituyen una organización de las actividades de aprendizaje que se realizarán con los alumnos y para los alumnos, con la finalidad de crear situaciones que les permitan desarrollar un aprendizaje significativo”. Es claro que la idoneidad no se alcanza a la primera, pero su estructura permite una aproximación razonable a lo que se desea y se sustenta en la retroalimentación, lo que permite el mejoramiento continuo de la propuesta diseñada.

2.2 Aspectos metodológicos

El presente trabajo corresponde a una investigación-acción con enfoque cualitativo basado en el modelo elaborado por ^{Kemmis (1998)} con las siguientes características: i) busca mejorar la calidad del proceso de aprendizaje mediante el estudio de una situación social como lo es el aula de clase (^{Elliott, 1993}). ii) se orienta a explicar el fenómeno desde sus características más sobresalientes (^{Bonilla & Rodríguez, 2000}).

La investigación se adelantó durante los dos primeros periodos del año escolar 2018, en el Colegio Integrado Juan Atalaya de la ciudad de Cúcuta. La institución está conformada por seis sedes, las cuales abarcan desde preescolar hasta grado once. La sede escogida fue la sede Central, de la jornada de la mañana, en la cual se encuentran los grados noveno, décimo y once; además, recibe 16 cursos de Jornada Única en los grados séptimo y octavo. La población objeto de estudio fueron los 142 estudiantes de grado noveno, conformado por hombres y mujeres con edades que oscilan entre los 14 y 17 años, que viven en barrios del sector, de estratos socioeconómicos 0 a 2. La muestra donde se aplicó el instrumento de evaluación fue de 33 estudiantes del grado 9-01.

Las fases de la metodología se llevaron a cabo de acuerdo al modelo de diseño mencionado anteriormente. Cada etapa está relacionada con las otras de forma secuencial. La prueba Saber evalúa las competencias básicas en los estudiantes de 3°, 5° y 9 grado; dicha prueba está enfocada en las áreas de lenguaje, matemáticas y ciencias naturales. En el área de matemáticas, la prueba está centrada en tres competencias, de acuerdo a los cinco tipos de pensamiento, establecidas en los Estándares Básicos de Competencias: numérico-variacional, métrico-espacial y aleatorio (MEN, 2006).

Se diseñó e implementó una prueba diagnóstica a los estudiantes de la muestra, la cual permitió conocer su nivel en las competencias de comunicación, razonamiento y solución de problemas. Esta prueba se realizó en dos etapas, una con 59 preguntas que se seleccionaron de la plataforma web de Supérate con el Saber, para los grados 3º y 5º del año 2017, y otra donde se seleccionaron 21 preguntas del cuadernillo de las pruebas Saber 3°, 5° y 9°, centradas en el pensamiento numérico-variacional.

A partir de los resultados del diagnóstico, se determinó desarrollar secuencias didácticas mediadas con TIC que fortalecieran: las competencias comunicativas, las de razonamiento abstracto y las de interpretación y solución de problemas en los estudiantes de grado noveno. La idea es fortalecer el desarrollo de competencias mediante un papel activo de los estudiantes, en un entorno mediado por TIC.

Durante 2017 se realizó un trabajo de pilotaje con estudiantes del grado 9-05, quienes asistían a la sede central y en la jornada de la tarde. Dicho grupo estaba conformado por 42 estudiantes, cuyas edades oscilaban de 13 a 17 años. El enfoque del instrumento se centró en el razonamiento algebraico de ^{Godino y Font (2003)} y de esa manera fue seleccionada una prueba diagnóstica que había sido desarrollada por ^{Ospina (2015)}, referente de esta investigación. Sin embargo, los resultados evidenciaron tantos vacíos en conocimientos previos, que el instrumento no permitió medir las características que se deseaban estudiar, haciendo muy pobre su validez. Por este motivo, fue necesario definir otro criterio para el diseño de la prueba diagnóstica, uno que se centrara en los aspectos más básicos y estructurales del pensamiento variacional.

Los instrumentos utilizados, como las preguntas aplicadas en la Prueba Diagnóstica y en la Prueba de Cierre, fueron tomados de la página web del ICFES y Supérate con el Saber 2017, lo que indica que ya han sido validadas por estas entidades. El material aplicado a los estudiantes fue sometido a revisión por parte de algunos miembros de la línea Educación Matemática, del Grupo de investigación EDUMATEST, de la Universidad de Pamplona.

3.1 Primera prueba diagnóstica de presaberes

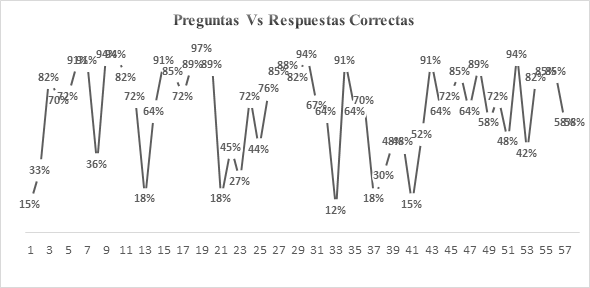
Los resultados de la primera parte de la Prueba Diagnóstica se reflejan en la Figura 2, donde se evidencia que los Indicadores 1, 5, 8, 17 y 23 no estaban apropiados por el grupo de estudiantes en un rango superior al 80%. Es necesario recalcar que los indicadores chequeados y las preguntas aplicadas, hasta ahora, eran de 3° y 5°, lo que hacía urgente aplicar una estrategia didáctica que permitiera nivelar estos vacíos, antes de aplicar la segunda parte del diagnóstico.

Figura 2 Resultados del diagnóstico inicial: presaberes. 

A continuación se relacionan los indicadores encontrados con las dificultades más sobresalientes: Indicador 1, resolver situaciones en las que se realicen sumas y multiplicaciones para encontrar su solución; Indicador 5, resolver situaciones que requieran lectura e interpretación de gráficas y tablas, en particular pictogramas; Indicador 8, realizar experiencias en compraventa en la que se tenga que contar dinero; Indicador 17, armar figuras planas con piezas; Indicador 23, realizar experiencias en las que tenga que combinar dos, tres o más elementos. Estos resultados evidencian que los estudiantes no estaban familiarizados con el estilo de preguntas, lo que afectó significativamente su rendimiento.

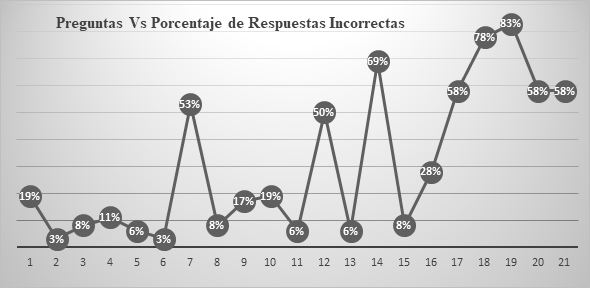
3.2 Prueba diagnóstica en pensamiento matemático variacional

En esta etapa la prueba aumenta el grado de dificultad de las preguntas, aun así, los resultados fueron relativamente mejores; sin embargo, se han encontrado seis indicadores: 6, 12, 14, 15, 16, 17 y 18, que se destacan por no estar presentes en más de la mitad de los estudiantes del curso, ver Figura 3. Estos son: Indicador 6, generar equivalencias entre expresiones numéricas; Indicador 12, justificar y generar equivalencias entre expresiones numéricas; Indicador 15, resolver problemas en situaciones de variación con funciones polinómicas y exponenciales; Indicador 16, identificar y describir las relaciones (aditivas, multiplicativas, y de recurrencia) que se pueden establecer en una secuencia numérica; Indicador 17, resolver problemas en situaciones aditivas y multiplicativas en el conjunto de los números reales; Indicador 18, verificar conjeturas acerca de los números reales, usando procesos inductivos y deductivos desde el lenguaje algebraico.

Figura 3 Resultados de la evaluación diagnóstica en pensamiento variacional. 

3.3 Secuencia pedagógica con mediación TIC

La propuesta pedagógica aplicada fue titulada como Aula-TIC-Matemática. Se recogieron ocho secuencias didácticas, las cuales fueron diseñadas de acuerdo a las necesidades específicas de aprendizaje de los estudiantes objeto de investigación y basadas en el aprendizaje significativo y colaborativo. Dichas necesidades surgieron del diagnóstico en pre saberes de matemáticas y en pensamiento variacional, los cuales fueron aplicados en la primera y en la tercera semana de clases. El propósito de la propuesta fue desarrollar situaciones de aprendizaje donde el pensamiento variacional y las estrategias TIC, favorecieran el aprendizaje matemático en el aula.

Las secuencias didácticas se enmarcaron en el plan de área establecido para la signatura de matemáticas de noveno grado, para el primero y segundo periodo del año escolar 2018. Siguiendo el orden del capítulo de los números reales, definido en el libro del estudiante “Vamos a Aprender - Matemáticas 9”. Cada secuencia se compone de tres momentos que son: Apertura, Desarrollo y Cierre. En la Apertura, los estudiantes evocan sus presaberes. En el Desarrollo, valiéndose del trabajo colaborativo y del texto, se ejecutan las actividades planificadas con la mediación de las TIC, procurando un aprendizaje significativo. En el Cierre, se concretizan los aprendizajes alcanzados después de la actividad desarrollada.

En el aula TIC de matemáticas se dispone de: video beam, computador portátil, tablero digital, tablero acrílico, audio y disponibilidad de tabletas. Para cada secuencia, el docente previamente ha elaborado una presentación en PowerPoint de manera que se tenga claridad en todo momento de lo que se está haciendo, se han temporizado las actividades para que exista un control en el tiempo. Los estudiantes han recibido el Libro del estudiante de Matemáticas y trabajan en parejas.

3.4 Análisis de la prueba de cierre en pensamiento numérico variacional

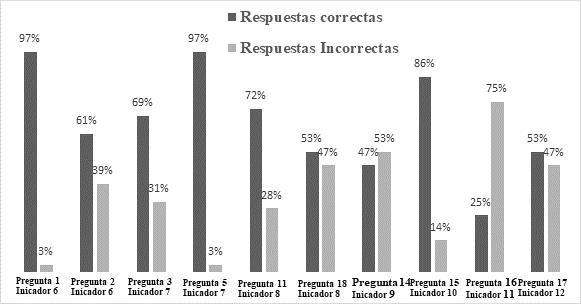
El análisis de los resultados por competencia permite evaluar los avances positivos en cuanto a la comunicación, representación y modelación, ver Figura 4. La mayoría de los indicadores presentan progresos significativos, que al evaluarse respecto a los indicadores iniciales del problema dan cuenta del éxito de la estrategia de intervención pedagógica implementada.

Figura 4 Resultados para competencia comunicativa en prueba de cierre en pensamiento variacional. 

En cuanto a la Competencia Razonamiento y Argumentación, se percibe el sostenimiento de una tendencia negativa, pues la mayoría de los estudiantes contestó de manera incorrecta. La figura 5 así lo evidencia.

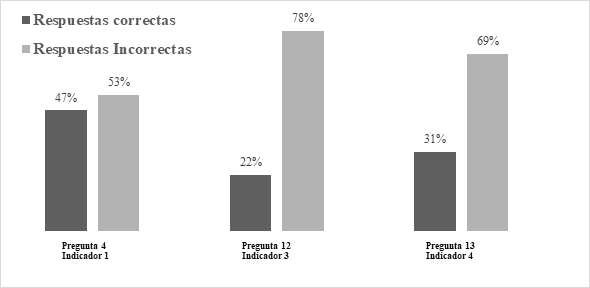
Figura 5 Resultados para competencia de razonamiento y argumentación en prueba de cierre en pensamiento variacional. 

En cuanto a la competencia: Planteamiento y Solución de Problemas, se perciben avances en las respuestas correctas en la prueba final. Esto parece indicar que la estrategia pedagógica posibilitó progresos importantes en la formación en la competencia mencionada, y que permite, además, sugerir que los estudiantes avanzan en el fortalecimiento del pensamiento variacional, ver Figura 6.

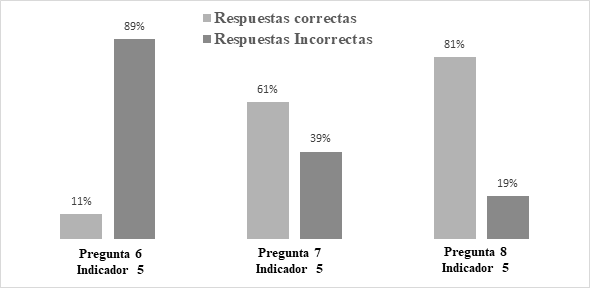
Figura 6 Resultados para competencia de planteamiento y solución de problemas en prueba de cierre en pensamiento variacional. 

Como síntesis de los resultados de la prueba de cierre, se puede decir que es indiscutible que existen varios aspectos por mejorar en el desarrollo del pensamiento variacional, especialmente en el razonamiento y argumentación. Sin embargo, el proceso adelantado con los estudiantes evidencia que hay una evolución, desde el momento en que se aplica el primer diagnóstico y hasta cuando se someten a la prueba de cierre. El mecanismo de choque es el mismo, resolver los ejercicios en el tablero, socializar: ¿por qué se equivocaron? o ¿qué pensaron para finalmente acertar con la respuesta?; ambientes de participación donde el centro es el modo de argumentar de los estudiantes.