1. Introducción
Resulta de gran interés el estudio de los procesos de enseñanza y aprendizaje del álgebra en diversas agendas de investigación (Kieran, 2006; Martínez-López & Gualdrón-Pinto, 2018), así como también en su aprendizaje (Cajaraville et al., 2012). Las investigaciones reportan las dificultades que se evidencian en los estudiantes, cuando se enfrentan a tareas relacionadas con el desarrollo del pensamiento variacional: por ejemplo, obstáculos cognitivos, ausencia de sentido de los sistemas de representación o actitudes afectivas y emocionales. Estas dificultades se asocian a los procesos de evolución del pensamiento algebraico en los estudiantes, que provocan que los conocimientos adquiridos, en una determinada etapa, se conviertan en modelos implícitos inadecuados para adquisición de nuevos conocimientos (Flores-López & Auzmendi-Escribano, 2017).
Un aspecto relevante a la hora de intentar abordar la problemática tiene que ver con la comprensión de las características de los diseños instruccionales y, en general, los medios que se usan en el aula de clase para desarrollar la actividad matemática (Muñoz-Mesa et al., 2014; García-Quiroga, Coronado & Giraldo-Ospina, 2017). En este sentido, Borba y Villarreal (2005), plantean que dichos medios condicionan la actividad matemática que se intenta desarrollar en las clases de matemáticas. Entre los medios usados en el aula de clase, se encuentran las baldosas algebraicas y los manipuladores virtuales, que son herramientas que, entre otras cosas, facilitan el trabajo con polinomios (Valderrama, 2015).
En el presente artículo se exponen y discuten los resultados de la aplicación de una unidad didáctica, que sirvió como una herramienta metodológica de enseñanza aprendizaje, donde el estudiante asume su proceso de aprendizaje desde un enfoque lúdico, y con la cual se pretendió potenciar el pensamiento variacional, particularmente en relación a los polinomios y operaciones entre ellos. La propuesta de intervención pedagógica, aplicada con estudiantes de octavo grado de la Institución Educativa la Garita, se basó en la manipulación de material concreto y virtual. Este material sirve como soporte que favorece la enseñanza de la adición, la sustracción, la multiplicación y la descomposición factorial de polinomios, a partir de representaciones geométricas, que permiten hacer la transición entre los sistemas semióticos, pasando del lenguaje natural al algebraico y geométrico, buscando que los estudiantes tengan un aprendizaje significativo y avancen en el pensamiento variacional.
La estrategia propuesta es una herramienta que permite al docente apartarse de la enseñanza tradicional en diversos temas del álgebra, convirtiéndose en una alternativa para la construcción de los conceptos abstractos de las matemáticas. Durante su desarrollo, se aplicó la metodología de investigación acción con enfoque cualitativo, partiendo de un diagnóstico, diseñando una estrategia a partir de una unidad didáctica y evaluando los resultados mediante el análisis de las producciones de los estudiantes, que mostraron avances significativos en el desarrollo del pensamiento variacional.
2. Marco teórico y metodología
2.1 Referentes teóricos
La enseñanza de la matemática en entornos educativos
Cuando se realiza un diseño instruccional para desarrollar un objeto matemático, una de las preocupaciones principales del docente radica en cómo mantener a los estudiantes interesados en el tema que se va a tratar. Más aún, cómo estructurar el discurso didáctico para atraer y mantener la atención de los estudiantes. Después de todo, “el docente de matemática tiene, por lo general, el estigma de ser el profesor de una materia difícil y aburrida”, así lo señala Gardner (1995).
La enseñanza de la matemática es, según Gallego (2007), “un proceso didáctico de aspectos lógicos y analíticos, a través de los cuales el estudiante debe aprender a pensar y razonar”. De allí que, los estudiantes aprenden su aplicación en la práctica cotidiana, su relación con otras asignaturas y las ventajas futuras. En el mismo orden de ideas, Aja (2001), refiere que el aprendizaje está “considerado como un proceso psico-cognitivo, fuertemente influenciado por factores motivacionales y actitudinales del estudiante”. Es así que, el docente juega un papel protagónico en el sentido de generar las motivaciones y actitudes positivas hacia el área de matemáticas, planeando los procesos de enseñanza y aprendizaje desde un enfoque constructivista, por ejemplo, separándose de los enfoques tradicionalistas, memorísticos y pasivos, para así impactar positivamente los resultados del aprendizaje.
De esta manera, el proceso de enseñanza aprendizaje de las matemáticas impone en el quehacer del docente, un análisis que brinda salidas eficientes desde una posición didáctica, en la cual se seleccionan objetivos, contenidos, métodos y evaluación apropiada. Esto da lugar a la planificación como herramienta indispensable para el análisis de los diferentes aspectos vinculados con los contenidos escolares; es decir, se aclara: qué, cómo y para qué se lleva a cabo la tarea de enseñar.
Respecto a la planificación, Antúnez (2002), la define como: “proceso reflexivo sobre la práctica, reporta calidad a la enseñanza, facilita la autonomía pedagógica al aumentar su capacidad de decisión e investigación de lo que acontece en el aula, debe ser flexible, contextualizada y completa”. Es decir, que puede ser vista como un camino mediante el cual se determinan las metas y se establecen los requisitos para lograrlas de la manera más eficiente y eficaz posible. Por consiguiente, el docente debe ser cuidadoso en el diseño de la misma, indagando información significativa para el estudiante, con el fin de ser innovador y creador de su praxis pedagógica.
Asimismo, la enseñanza de la matemática, según Gutiérrez (2000), debe estar enfocada en tres tópicos: utilizar la matemática conocida como herramienta para resolver problemas cotidianos; aprender a enseñar matemáticas, lo cual provee al estudiante herramientas necesarias para solucionar problemas nuevos y al mismo tiempo mantiene vivo su saber; por último, crear matemática novedosa, adoptando modelos conocidos a las necesidades del estudiante, de modo que los apliquen en situaciones nuevas.
En este sentido, el aprendizaje debe tener lugar en ambientes reales dentro y fuera del aula, vinculando las actividades seleccionadas con las experiencias vividas por el estudiante. En otras palabras, hay que integrar la actividad (ejercitación), concepto (conocimiento) y cultura (contexto); lo cual está estrechamente relacionado con lo propuesto por los Lineamientos Curriculares de Matemáticas, del Ministerio de Educación Nacional colombiano, MEN (1998). Es así que el docente debe esforzarse en obtener aprendizajes significativos basados en la experiencia, analizando, junto con los estudiantes, las respuestas que han dado a las actividades programadas y relacionar sus conocimientos previos con los contenidos. Lo anterior para dar lugar al aprendizaje de los nuevos conocimientos, desde la memoria inicial hasta la formación de conceptos, teniendo en cuenta el estilo de aprendizaje de cada estudiante.
En síntesis, es necesario reconceptualizar el rol del docente e identificar las habilidades que debe poseer, como: ser: un investigador capaz de diseñar y evaluar estrategias que le permitan resolver los problemas de la realidad, planificar la acción pedagógica, prever los recursos disponibles, aplicar motivación apropiada, explorar conocimientos previos, contenidos y recursos para construir nuevos conocimientos y lograr aprendizajes efectivos.
Pensamiento variacional
Según el MEN (2006), “este tipo de pensamiento tiene que ver con el reconocimiento, la percepción, la identificación y la caracterización de la variación y el cambio en diferentes contextos, así como su descripción, modelación y representación en distintos sistemas o registros simbólicos, ya sean verbales, icónicos, gráficos o algebraicos”.
El desarrollo del pensamiento variacional es un proceso que requiere de los conocimientos y la relación de los pensamientos numérico, geométrico y métrico, por parte de los estudiantes, y de estrategias didácticas por parte del docente. Esto debido a que es “lento y complejo, pero indispensable para caracterizar aspectos de la variación, tales como: lo que cambia y lo que permanece constante, el campo de variación de cada variable y las posibles relaciones entre las variables” (MEN, 2006).
El objetivo central del pensamiento variacional es la modelación matemática. Los ejercicios que se les proponen a los estudiantes deben convertirse en retos o desafíos, que requieran de la realización de un modelo para su solución y no solo la simple realización de ejercicios rutinarios, que se resuelven repitiendo algoritmos (Vasco, 2002; Villamil-Rincón, Aldana-Bermúdez & Wagner-Osorio, 2018).
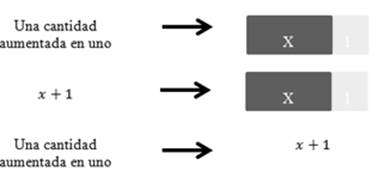
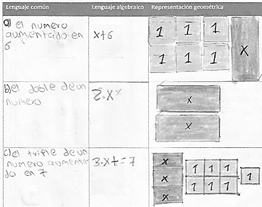
En el estudio aquí presentado, la propuesta incluye el uso de registros semióticos, verbales, algebraicos y geométricos. Así mismo, la construcción de modelos geométricos de expresiones algebraicas y la identificación de invariantes. Al respecto, Duval (1999) sugiere que en los diferentes niveles de enseñanza de las matemáticas, se puede observar la persistencia de un encerramiento entre representaciones que no proviene del mismo sistema semiótico. El pasaje de un sistema de representación a otro, o la movilización simultánea de varios sistemas de representación en el transcurso de un mismo recorrido intelectual, fenómenos tan familiares y tan frecuentes en la actividad matemática, para nada son evidentes o espontáneos para la mayoría de los alumnos (Duval, 1999). A manera de ejemplo y como se tuvo en cuenta en este estudio, en la figura 1 se muestra una expresión en tres representaciones semióticas.
En este sentido, Socas, Camacho, Palarea y Hernández (1989) sugieren que el uso de más de un lenguaje para representar un concepto favorece la abstracción del concepto, ya que tenemos más puntos de referencia y permiten establecer así más relaciones. Por otro lado, el hecho de presentar un concepto de formas diversas hace que a este se le conozca en más facetas de las que normalmente se le considera cuando se hace el aprendizaje con un solo lenguaje.
En el ejemplo de representación semiótica de la figura 1, se pueden evidenciar las bondades de un sistema o de otro; en lenguaje natural, una cantidad aumentada en uno, puede que para algunos estudiantes no represente mucho; sin embargo, al observar un rectángulo (color gris oscuro) junto con un cuadrado (color gris claro) cuya área es: x y 1 unidades cuadradas respectivamente, permite potenciar su representación mental, al punto que el observador realiza las asignaciones presentadas en la figura 2 para realizar una mejor interpretación.
Expresiones algebraicas
En la literatura existen diferentes definiciones de lo que es una expresión algebraica. Los libros de texto escolar la definen como: la combinación de letras con o sin números reales, relacionados unos con otros por medio de las operaciones de adición, sustracción, multiplicación, división y potenciación de exponente racional. Las expresiones algebraicas tienen su papel preponderante en el aprendizaje de las matemáticas escolares, en la medida que se establezcan relaciones entre unas y otras; estas relaciones pueden ser: operaciones entre expresiones algebraicas, transformaciones, representaciones, planteamiento de ecuaciones e inecuaciones.
Según Nemirovsky (1996, citado por Torres, Valoyes & Malagón, 2002), las expresiones algebraicas cobran realmente su dimensión matemática cuando se relacionan y operan, produciendo ecuaciones, inecuaciones y nuevas expresiones algebraicas. En el surgimiento de estos objetos algebraicos aparece el problema de la producción de significado de estos constructos. Esto ha sido ampliamente debatido por distintos investigadores, quienes sustentan la necesidad de trabajar con los estudiantes diversas aproximaciones, por ejemplo, al concepto de ecuación para que ellos las puedan significar.
Baldosas algebraicas
Es un material concreto, manipulable y didáctico, que se usa principalmente en la enseñanza de tópicos del álgebra. Consiste en un conjunto de paralelepípedos de diferentes colores y dimensiones, comúnmente de plástico, donde una de las caras coincide con al menos una de otra baldosa; poseen una altura ínfima, por tal razón, se tiene en cuenta únicamente su vista superior o inferior y sus dos dimensiones: el ancho y el largo. La figura 3 muestra diferentes baldosas algebraicas y su representación algebraica.
Manipuladores virtuales
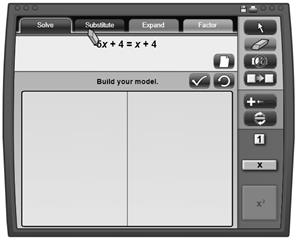
Es un conjunto de software matemático para la enseñanza del álgebra. De manera particular se empleó el Algebra Tiles, aplicación desarrollada por el National Council of Teachers of Mathematics (NCTM). La aplicación permite representar expresiones algebraicas con modelos geométricos y de esta manera resolver ecuaciones, multiplicar y factorizar polinomios algebraicos. La figura 4 muestra la interface del software.
2.2 Aspectos metodológicos
Enfoque y tipo de investigación
Este trabajo es de enfoque cualitativo, tipo investigación acción, dado que se centra en la reflexión de un problema práctico, cotidiano, experimentado por los profesores y estudiantes en las aulas de clase, en particular de grado octavo. Se requiere de contacto directo con el entorno o ambiente donde se sitúa la investigación, permitiendo que se desarrolle un proceso de retroalimentación constante entre el investigador y el individuo que forman parte de la realidad estudiada, donde no interesa dimensionar magnitudes, sino explorar naturalezas, las cuales se conciben desde múltiples perspectivas, apoyándose en los diferentes métodos cualitativos pertinentes como vía de obtención de conocimientos.
En este sentido, Elliot (1993) expresa: “podemos definir la investigación acción como el estudio de una situación social para tratar de mejorar la calidad de la acción en la misma” (p. 88).
Así, se entiende la investigación acción como: la reflexión sobre las situaciones vividas por los docentes en el entorno educativo y tiene como objetivo realizar una comprensión de sus problemas y de encaminar acciones que modifiquen o den solución a la situación experimentada. En el desarrollo del presente estudio se toma en cuenta el ciclo de la investigación acción como eje orientador (Corbetta, 2010, citado por Jiménez-Espinosa & Sánchez-Bareño, en prensa).
Fase de Planificación: en la planificación se tuvo en cuenta el diseño de una unidad didáctica como estrategia metodológica y lúdica, de manera que se adecúe el conocimiento matemático al contexto de los educandos, se estructure el proceso de enseñanza aprendizaje y se evite la improvisación.
Fase de acción: se intervino al grupo con la unidad didáctica titulada “La cobija de mi abuelo está hecha de retazos”. La intervención se realizó en dieciséis encuentros durante cuatro meses. Dichos encuentros buscaron, en primer lugar, dotar a los estudiantes de herramientas conceptuales y actitudinales para potenciar el aprendizaje; en segundo lugar, desarrollar las bases teóricas para generar los conceptos matemáticos y, por último, aplicar el conocimiento adquirido en la comprensión o formulación de las propiedades características de los conceptos desarrollados.
Fase de observación: en esta fase se utilizó el diario pedagógico para registrar las actitudes, habilidades, destrezas y conocimientos de los estudiantes observados en las intervenciones, de manera que suministraran información relevante, susceptible de ser analizada. Igualmente, se recogieron las producciones realizadas por los estudiantes durante los encuentros, con el fin de realizar una comparación y reflexión a la luz de las categorías, subcategorías e indicadores de análisis.
Fase de reflexión: esta fase estuvo dirigida a la generación de espacios de reflexión, para fortalecer las prácticas pedagógicas de aula, a través de los hallazgos encontrados en los registros de los diarios pedagógicos y las producciones de los estudiantes, que permitieron realizar una comprensión de la problemática planteada. Además, se hizo la propuesta de una alternativa de solución, con el fin de potenciar el desarrollo del pensamiento variacional en los estudiantes de grado octavo de la Institución Educativa.
La población objeto de estudio estuvo constituida por 39 estudiantes del grado octavo, de la institución educativa La Garita. Se trata de una institución de carácter oficial, ubicada en la vereda La Garita del Municipio de Los Patios, en Norte de Santander. Las edades de los estudiantes oscilan entre los 13 y 16 años, en su gran mayoría pertenecientes al sector rural del municipio, con un nivel socio económico 1 y 2. La intervención se desarrolló en dieciséis encuentros, de dos horas cada uno, durante el primer semestre del año 2018.
Categorías de análisis
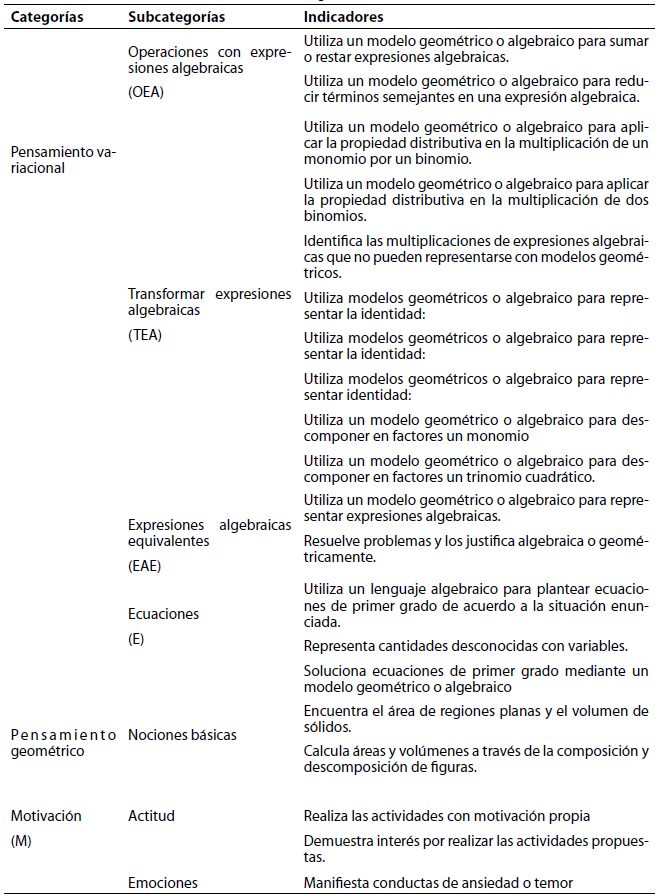
Para el diseño de las categorías de análisis se tuvieron en cuenta documentos como: Lineamientos Curriculares, Estándares Básicos de Competencia y Derechos Básicos de Aprendizaje del MEN. Con base en dichos documentos se plantearon unas categorías y subcategorías a priori, lo cual indica que es perfectamente plausible que emergieran otras que no se contemplaron, a la luz del análisis y la reflexión de las categorías iniciales en las producciones de los estudiantes. En la tabla 1 se presentan las categorías y subcategorías de análisis, mostrando los indicadores para evaluar las producciones de los estudiantes en las intervenciones pedagógicas.
3. Resultados y discusión
3.1 Prueba diagnóstica
Al analizar la totalidad de las producciones realizadas por los estudiantes durante la prueba diagnóstica, se evidenciaron los siguientes hallazgos: i) la gran mayoría de los estudiantes desconocen las fórmulas básicas de geometría para el cálculo de las áreas de regiones planas y de volúmenes; ii) los estudiantes asignan un valor numérico a las variables para poder realizar los cálculos aritméticos; iii) los estudiantes memorizan algunas fórmulas de áreas de regiones planas y volúmenes, pero no las aplican en contextos algebraicos; iv) la gran mayoría de los estudiantes desconocen la utilidad de las letras en situaciones problema, no dan significado a la variable y no la tienen en cuenta para realizar las operaciones de adición, sustracción y multiplicación.
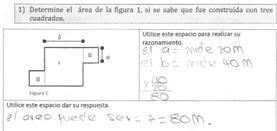
A manera de ejemplo se presentan algunas de las producciones de los estudiantes. En la figura 5 se observa la producción del participante N° 31, él divide el cuadrado I en rectángulos de tamaño similar al cuadrado II, pero se da cuenta que no se puede dividir en partes iguales; el participante agrega: “con la ayuda de una regla lo podría solucionar”.
La figura 6 corresponde a la producción del participante N° 23, él asigna valores numéricos a las letras (a y b) con el fin de poder operar numéricamente. Se observa cómo el participante intenta resolver la situación con operaciones aritméticas, asignando un valor arbitrario a las letras y operándolas de una manera incorrecta, con el propósito de dar una respuesta numérica.
3.2 Intervenciones pedagógicas
En esta sección se presenta un análisis descriptivo de algunos ejemplos paradigmáticos de producciones de estudiantes durante la intervención, la cual se dividió en tres actividades: inicio, desarrollo y aplicación. En este sentido, se hará un recorrido mostrando el avance que fueron adquiriendo los estudiantes a medida que se intervenía al grupo con la unidad didáctica.
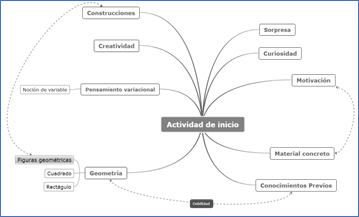
Actividad de inicio
En la figura 7 se presenta un mapa de conceptos que resume los hallazgos encontrados durante la actividad de inicio. Se puede observar cómo el material concreto despertó la curiosidad y la sorpresa en los estudiantes sirviendo como detonante de la motivación, la cual permitió desarrollar construcciones con creatividad y activar los conocimientos previos.
En la figura 8 se observan las representaciones que realizó el participante N° 5 en el paso de un sistema de representación semiótico a otro: pasó del lenguaje natural al lenguaje algebraico, realizando su representación geométrica. El estudiante interpreta que un número cualesquiera puede ser representado con una letra del alfabeto, utiliza la letra x para referirse a un número cualesquiera. De manera similar interpreta palabras claves que sugieren operaciones como: duplo, triple, doble, entre otras. En la producción del participante N° 5 se cumplió con el indicador: utiliza un modelo geométrico o algebraico para representar expresiones algebraicas de la subcategoría Expresiones algebraicas Equivalentes (EAE)
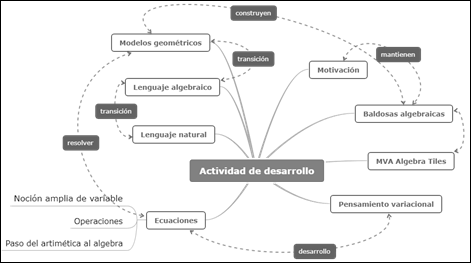
Actividad de desarrollo
La figura 9 corresponde a un mapa de conceptos de la actividad de desarrollo. En él se puede observar el papel preponderante que tienen las baldosas algebraicas y los manipuladores virtuales, primero para mantener la motivación de los participantes y, segundo, para desarrollar las nociones matemáticas. Los modelos geométricos que se construyeron durante la actividad de desarrollo, permitieron ampliar el registro de representaciones semióticas y transitar desde el lenguaje algebraico, al natural y a la representación geométrica; además, el manejo del material favorece la construcción de la noción de variable, la resolución de ecuaciones y el paso de la aritmética al álgebra, dando indicios del desarrollo del pensamiento variacional.
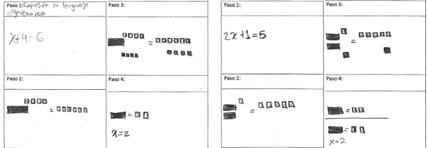
Resolución de ecuaciones
En la figura 10 se observan los procedimientos que utilizó el participante N° 35 para resolver dos ecuaciones: una ecuación de la forma: x+b=c y, la otra, de la forma: 𝑎𝑥+𝑏=𝑐. Se destaca el buen desempeño que presentó el participante durante los ejercicios propuestos. El participante logró asimilar el procedimiento sugerido en el manipulador virtual para resolver este tipo de ecuaciones, utilizando un modelo geométrico. Claramente, el participante cumple con el indicador: soluciona ecuaciones de primer grado utilizando modelos geométricos o algebraicos, perteneciente a la subcategoría Ecuaciones (E).
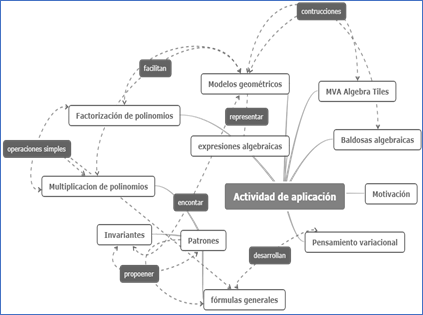
Actividad de aplicación
La figura 11 corresponde a un mapa de conceptos durante la actividad de aplicación. En él se observa la manera como las baldosas algebraicas y el aplicativo Algebra Tiles facilitaron el desarrollo de pensamiento variacional. El material concreto y el aplicativo virtual motivaron a los participantes para que entendieran las operaciones de: adición, sustracción, multiplicación y descomposición factorial de polinomios, realizando modelos geométricos. Posteriormente, los participantes identificaron invariantes en las respuestas de algunas identidades, conduciendo de esta manera a fórmulas generales para la multiplicación y la descomposición factorial de trinomios.
Multiplicación de la suma por la diferencia de binomios (a+b)(a-b). El desempeño de los participantes durante este encuentro fue destacable. La mayoría de ellos no tuvo inconvenientes al representar gráficamente las multiplicaciones de los binomios. Los estudiantes recordaron sin dificultad la propiedad uniforme de las igualdades y la aplicaron en la solución de los ejercicios propuestos. Algo para resaltar en este encuentro, fue la competencia que se generó alrededor de las construcciones. Un grupo numeroso de participantes compitió entre ellos para ver quien terminaba primero la actividad; en medio de esa competencia, el participante N° 38 comenta: “profe y eso que decían que el álgebra era difícil, le meten miedo desde sexto y mire, es fácil”. El participante N° 32 le replica: “es fácil porque estamos trabajando con las baldosas”. En la intervención de los participantes N° 38 y N° 32, se generó un entorno de sana competencia, lo que sugiere la presencia de la categoría Motivación (M). Los participantes realizaron las actividades con agrado.
En este sentido, los participantes socializaron sus construcciones, proyectándolas al grupo con ayuda del aplicativo Algebra Tiles. El software ha permitido que se realice la retroalimentación de una manera más eficiente, porque el aplicativo da la posibilidad de valorar las construcciones que se hacen y presenta las representaciones geométricas en lenguaje algebraico. En términos generales, se puede afirmar que el propósito planteado se cumplió satisfactoriamente. A continuación se presentan algunas de las producciones realizadas por los participantes.
La figura 12 corresponde a la producción realizada por el participante N° 14. Se observa que representa el producto utilizando un modelo geométrico, de manera similar aplica la propiedad uniforme de las igualdades y, por último, encuentra el producto de los binomios expresándolo en lenguaje algebraico. Se evidencia en la producción, que el participante cumple con los indicadores. Utiliza un modelo geométrico o algebraico para representar expresiones algebraicas, utiliza un modelo geométrico o algebraico para aplicar la propiedad distributiva de la multiplicación de dos binomios; esto sugiere la presencia de las subcategorías Expresiones Algebraicas Equivalentes (EAE) y Transformar Expresiones Algebraicas (TEA).

Figura 12 Producción del participante N° 14, multiplicación de la suma por la diferencia de dos binomios.
El mismo participante encuentra algunos invariantes y propone una fórmula general para encontrar el producto de la suma por la diferencia de dos binomios; aunque los invariantes son acertados, la propuesta de la fórmula general presenta algunos errores gramaticales. El participante no expone con claridad su idea; sin embargo, escribe en lenguaje algebraico una fórmula acertada para encontrar el producto.
Descomposición factorial de trinomios de la forma x 2 +bx+c. La figura 13 corresponde a la producción realizada por el participante N° 13. En su trabajo se observa que él representa acertadamente los trinomios utilizando un modelo geométrico, encuentra la base y la altura del rectángulo y encuentra unos invariantes para un caso en particular. El participante da cuenta que al multiplicar y sumar los segundos términos de los binomios, estos resultados son iguales a los coeficientes del segundo y tercer término del trinomio. En la producción del estudiante se evidencian los indicadores: Utiliza un modelo geométrico o algebraico para descomponer en factores un trinomio cuadrático perteneciente a la subcategoría, Transformar Expresiones Algebraicas (TEA), y el indicador: Utiliza un modelo geométrico o algebraico para representar expresiones algebraicas pertenecientes a la subcategoría, Expresiones Algebraicas Equivalentes (EAE).
4. Conclusiones
La mayoría de los estudiantes desconoce las fórmulas básicas de geometría para el cálculo de las áreas y volúmenes de superficies planas y, cuando las conocen o recuerdan no las aplican en contextos algebraicos, lo que les impide abordar con diligencia la resolución de situaciones matemáticas.
La mayoría de estudiantes asigna arbitrariamente un valor numérico a las variables para poder realizar cálculos aritméticos, lo que sugiere un desconocimiento de la utilidad de la variable y de su significado en situaciones problemáticas.
La incorporación de la unidad didáctica en el proceso de enseñanza aprendizaje, permitió a los estudiantes abordar los objetos matemáticos abstractos de una manera significativa. Esto debido a que el material concreto y el aplicativo Algebra Tiles sirvieron de mediadores entre la construcción del conocimiento y los estudiantes, potenciando el desarrollo de los conceptos matemáticos abstractos a través de la manipulación de objetos a los cuales les pueden asignar un significado real.
La unidad didáctica impactó positivamente sobre la concepción que tienen los estudiantes de las matemáticas, generando en ellos motivación intrínseca, que permite abordar las diferentes temáticas desde una mirada lúdica, emocionante, inquietante y alcanzable para todos. Por otro lado, la unidad didáctica potenció el pensamiento variacional, lo que sugiere que en temáticas propias del curso y de las posteriores, los estudiantes tendrán mejor desempeño.