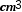1. Introducción
La Etnomatemática es un programa de investigación, que se ha encargado de mostrar y valorar las ideas matemáticas existentes en diversas experiencias cotidianas de todos los pueblos, de todos los grupos sociales y culturas humanas (Gerdes, 2013), destacándose las conexiones entre la matemática formal y la matemática que emerge en las labores de agricultores, pescadores, comerciantes, deportistas y cocineros, entre otros. La Etnomatemática es innovadora y permite que a través de conocimientos culturales, se enriquezca el repertorio del aprendizaje de las matemáticas, conectándolos con el currículo (Laurens, Ngilawayan & Pattiasina, 2019). También, la Etnomatemática se ha involucrado en los procesos de enseñanza y aprendizaje de las matemáticas (Mosquera, Rodríguez-Nieto & Suárez, 2015), donde se ha fomentado el uso de unidades de medidas no convencionales.
Rosa y Orey (2018), comparten la concepción de que la Etnomatemática integra las comunidades culturales con las actividades escolares, donde se conecten las prácticas culturales con la matemática desarrollada en las aulas, en los procesos de enseñanza y aprendizaje. El tema de las conexiones es reconocido y recomendado por entidades curriculares, como el National Council of Teachers of Mathematics, NCTM (2000), cuando indica que si los estudiantes hacen conexiones entre conceptos, definiciones, entre representaciones y entre las matemáticas y la vida real, es más probable que comprendan las matemáticas. En el estándar de proceso “conexiones”, se sugiere abordar en todos los grados escolares, junto a la resolución de problemas, razonamiento y prueba, comunicación y representación. Igualmente, se considera que las figuras geométricas como triángulos y círculos (en educación secundaria), se pueden representar de forma analítica, estableciendo conexiones entre la geometría y el álgebra (NCTM, 2000).
El NCTM (2000), plantea que, “los profesores deben ayudar a sus estudiantes a ver las conexiones entre la fórmula y el objeto real”, y en los grados de primaria los estudiantes deberían aplicar fórmulas para hallar el perímetro y área de figuras geométricas, mientras que en la educación secundaria: los estudiantes deben trabajar con fórmulas para encontrar el volumen y el área de prismas y cilindros.
Las investigaciones en Etnomatemática, han estudiado los conocimientos matemáticos que desarrollan las personas cuando realizan sus prácticas cotidianas. Por ejemplo, se han realizado investigaciones donde han posibilitado la educación intercultural, considerando la didáctica, aspectos curriculares y resaltando la pluralidad de las matemáticas vivas como esencia de la etnomatemática (Oliveras, 2006). También se han explorado las medidas de longitud usadas en la pesca (Chieus, 2009; Mosquera et al., 2015; Rodríguez-Nieto, Mosquera & Aroca, 2019); otras han enfatizado en la albañilería, procesos de medición y estimación (Rey & Aroca, 2011). Rodríguez-Nieto, Morales-Garcia, Muñoz y Navarro (2017), identificaron unidades de medida de capacidad, como: el litro, el cuartillo y la arpilla; Rodríguez-Nieto, Aroca & Rodríguez-Vásquez (2019), reconocieron la utilidad del saco, el bulto y el balde, en la elaboración de bollos de yuca. En la carpintería, Castro et al. (2020), identificaron nociones matemáticas, como: los procesos de conteo, diseños, simetrías en los barcos, y medidas como el metro, la pulgada y la tolerancia. Rodríguez-Nieto (2020), exploró las conexiones entre sistemas de medidas usados en siete prácticas cotidianas (ganadería, agricultura, entre otras).
A continuación, cronológicamente (2005-2020), se presentan algunas investigaciones en etnomatemática que han explorado conceptos geométricos en diferentes prácticas cotidianas y en artefactos culturales. En la cultura Bribri de Talamanca, Gavarrete y Vásquez-Hernández (2005), describieron la etnogeometría en las canastas y viviendas tradicionales identificando formas geométricas (canastas con fondo triangular, tejido romboidal y base superior circular, y vivienda con forma cónica). En la elaboración de las mochilas Arhuacas, Aroca (2008), reconoció tejidos con formas de espiral, ángulos y patrones figurales, gasas con ángulos que miden 7 cm de ancho y 81 cm de largo, los fondos de las mochilas, con diseños clasificados en espirales o caracol con trazos curvilíneos, anillos concéntricos con punto central (centro de homotecia), y fondos combinados entre anillos concéntricos y figuras tradicionales. Huapaya y Salas (2008) identificaron ideas de paralelismo y perpendicularidad en los edificios, palacios y templos, nociones de semejanzas, congruencias, proporcionalidad y escalas en el urbanismo, conos truncados y cilindros en la cerámica y orfebrería, y, estampados, grabado, paralelismo, perpendicularidad, traslaciones, rotaciones y semejanza en la textilería.
En las esculturas del parque arqueológico de San Agustín, Urbano (2010), identificó las transformaciones de traslación, rotación, simetría, rectángulos, circunferencias y perpendicularidad en la planeación, elaboración de monumentos, verificando las nociones geométricas en el software Cabri. Micelli y Crespo (2011), exploraron los tejidos guatemaltecos (de huipiles, sobrehuipiles o fajas), observando ejes verticales de simetría axial, traslaciones y en las guardas identificaron secuencias, paralelogramos y traslaciones. Observaron rombos concéntricos en los símbolos como el “rupan läp o rupan plato”. En el tocapus o poncho, identificaron cuadrados, simetrías y rectángulos, y, en los ponchos y fajas de los Mapuches, identificaron cuadriláteros, rombos, triángulos y simetrías. Oliveras (2012), enfatizó en el aprendizaje de la superficie de una figura geométrica (círculo), en un contexto etnomatemático a partir de un artefacto: el panimetro, usado para producir torta de pan.
En los diseños de los hipogeos, Aroca (2013), reconoció configuraciones geométricas, como: los romboides, patrones figurales, triángulos, mediciones, círculos caracterizados por sus colores, trazados, superficies planas y cóncavas, y vértices. Gerdes (2013), reconoció que los cesteros Bora, hacen: níjtyubane (paneras, cribas o cuencos, platos), con esteras cuadradas y bordes circulares con su diámetro. En estos artefactos observó ejes perpendiculares de simetría, simetría axial y rotacional considerando un ángulo, los cuadrados dentados concéntricos que están decorados por mariposas, tiras horizontales y verticales y en los abanicos bora, se observaron patrones. Gavarrete y Casis (2014), compararon el Nopatkuö de la cultura Talamanqueña (costa Rica) y el Kultrún de la cultura Mapuche (Chile-Argentina), los cuales son patrimonio cultural e importante para el desarrollo de tres áreas: i) uso de simetrías (centro axial) para mostrar planos cosmogónicos y los círculos para diferenciar las divisiones de significado mítico o ciclos; ii) elementos geométricos como el cono, círculo, rombo, triángulos, líneas perpendiculares, paralelas y oblicuas; y, iii) estudio de la geometría intrafigural.
En la repostería, específicamente en la elaboración de piononos, Agulló (2014), Agulló, Fernández-Oliveras y Oliveras (2014), y Fernández-Oliveras y Oliveras (2015), reconocieron que el obrador artesano considera la adición y la sustracción, la medida no convencional “dedo” y conceptos geométricos (rectángulo, cilindro y espiral), evidenciados cuando la masa está en forma rectangular horizontal, y luego, se enrolla tomando forma cilíndrica. En los diseños de los platos o copas de las culturas prehispánicas de los Pastos o Quillacingas, Aroca (2015), encontró movimientos y transformaciones en el círculo, la homotecia, frisos, triángulos, superficies cóncavas, ángulos, figuras zoomorfas o antropomorfas, traslaciones, patrones figurales. Los platos cóncavos los hicieron planos, para crear un ambiente de configuración con delimitaciones por anillos, sectores circulares y simetrías.
Gavarrete y Albanese (2015), en Argentina, encontraron que en los esquemas de las coreografías de las danzas de la chacarera, los bailarines realizan figuras geométricas (cuadrado, diamante y rombo), determinadas por la música y se presentan actividades haciendo énfasis en la medida de las diagonales, lados y amplitud de ángulos. Mientras que en Costa Rica, se enfatizaron el uso del idioma cabécar (lógica clasificatoria y uso de metáforas numéricas), haciendo conteos con un sistema de numeración en base quinaria. Gavarrete (2015), propuso un modelo de formación docente basado en etnomatemáticas indígenas, donde geométricamente encontró que los tres grupos estudiados tienen lenguas distintas (Ngäbére, Bribri y Cabécar), y utilizan clasificadores numerales para identificar los objetos que se agrupan o se cuentan según su forma geométrica (alargada, plana y redonda). En la vivienda tradicional arhuaca, De la Hoz, Trujillo y Tun (2017), reconocieron la medida de la base cuadrada de la casa, forma triangular del techo, la vivienda que es un paralelepípedo. También, se observaron patrones geométricos, nociones de paralelismo, perpendicularidad y usan medidas como la altura de la persona y la brazada. En el trabajo de Morales, Aroca y Álvarez (2018), sobre las artesanías de Usiacurí, encontraron formas de caracoles o espiral en las estructuras de alambre, el semicírculo y triángulos en las estructuras de bolsos. Observaron medidas como la cinta métrica, la botella para la forma circular, los dedos, la cuarta y el jeme, y nociones de rotaciones y traslaciones.
Bandeira-Bezerra y Lanner de Moura (2018), problematizaron prácticas culturales como la Kushma y la fabricación de arco y flecha de la cultura Ashaninka, en la formación inicial de profesores, identificándose mediciones y conceptos geométricos. Sari, Somakim y Hartono (2018), reconocieron edificios en la cultura Rumah ogan komering ulu, los cuales tienen forma piramidal y algunos motivos de decoración del hogar o grabado en forma de geometría. También existen investigaciones que han explorado conocimientos geométricos, como la de García-García y Bernandino-Silverio (2019), quienes identificaron que los conceptos de circunferencia, parábola, intersección de rectas y paraboloide están inmersos en la elaboración y uso del güilile. Laurens et al. (2019), estudiaron las matemáticas relacionadas con el contexto de las comunidades isleñas en Maluku, donde se hacen tejidos que pueden favorecer el aprendizaje de la geometría. Paternina-Borja, Muñoz-Granados, Pacheco-Muñoz y Aroca (2020), exploraron las simetrías respecto a un eje vertical (divide a la máscara del torito en dos partes iguales), simetría de molde empapelado y en los colores. Identificaron medidas no convencionales (el dedo y el lápiz). Además, en las decoraciones reconocieron triángulos y rombos.
Las investigaciones realizadas en México sobre etnomatemática, son escasas. Estas se han centrado en estudiar artefactos, medidas no convencionales y conceptos geométricos (García-García & Bernandino-Silverio, 2019; Rodríguez-Nieto et al., 2017); de hecho, García-García y Bernandino-Silverio (2019), sugieren que, es importante que el profesor y el estudiante haga conexiones entre conceptos geométricos. También existen investigaciones centradas en la educación indígena (Ávila, 2014), y en exploraciones de cálculo aritmético con comerciantes de un mercado (Palacio, 2019). Sin embargo, no se han analizado los procesos matemáticos involucrados en la gastronomía mexicana, la cual es diversa, con variedad de platos típicos en cada estado del país. El cultivo y producto fundamental en México es el maíz, útil en la elaboración de: tamales, elotes, pozoles y tortillas, entre otros (Espejel-García et al., 2016; Rodríguez et al., 2017). En particular, la tortilla “forma parte de la identidad culinaria de los mexicanos que viven en México o en el extranjero; es un componente básico de los antojitos, acompaña a los platillos festivos y es un suministro consuetudinario en la comida” (Calleja & Valenzuela, 2016, p. 161).
En la literatura sobre el tema de la tortilla, se encontró que López, Sovilla y Martínez (2015), analizaron el impacto del aumento del precio de la tortilla en el consumo de hogares de ingresos bajo y alto, en San Cristóbal de Las Casas, Chiapas. Espejel-García et al. (2016), caracterizaron a los consumidores de tortilla del Estado de México e identificaron las características del producto que demandan, y cuantificaron la correlación de estos aspectos con los niveles de ingreso y consumo. Estos autores indican que: “la tortilla (…) provee energía por su contenido alto de carbohidratos, y aporta: calcio, potasio, fósforo, fibra, proteínas y algunas vitaminas”. Rodríguez et al. (2017), caracterizaron la labor de la tortilla hecha en San Pedro del Rosal, Atlacomulco, concluyendo que el saber hacer constituye una herencia, así como una estrategia de generación de ingresos económicos.
Las investigaciones precedentes muestran la importancia de los estudios en etnomatemática, que enfatizan en la exploración de conceptos geométricos y sugieren hacer conexiones entre los mismos para la mejora de la comprensión matemática (García-García & Bernandino-Silverio, 2019); sin embargo, no se ha explorado la práctica cotidiana de la elaboración de tortillas. Otros trabajos muestran la importancia de la tortilla en el ámbito alimenticio, económico y cultural, de algunos sectores del país mexicano. No obstante, faltan investigaciones sobre la tortilla, cuyo enfoque sea contribuir al campo de la enseñanza y aprendizaje de las matemáticas y a las conexiones, por lo que es un tema adecuado para ser investigado. De hecho, “en la mayoría de los estudios fundamentados en el Programa Etnomatemática, poco se ha explorado la matemática inmersa en la gastronomía, donde se siguen procedimientos para la obtención de un producto alimenticio” (Rodríguez-Nieto et al., 2019). Por tal motivo, en este estudio se analizan las conexiones etnomatemáticas entre conceptos geométricos, que emergen en el proceso de elaboración de tortillas por un comerciante de Chilpancingo, Guerrero, México.
2. Marco teórico y metodología
2.1 Etnomatemática
La Etnomatemática se ha definido como un conjunto cociente, obtenido al valorar, reconocer y clasificar las prácticas matemáticas que realizan los grupos sociales y culturales (Oliveras, 1996; 2006). Sin embargo, la mayoría de los trabajos fundamentados en la Etnomatemática se han basado teóricamente en dos definiciones. En la primera, la Etnomatemática es “la matemática practicada por (…) comunidades urbanas o rurales, grupos de trabajadores, clases profesionales, niños de cierta edad, sociedades indígenas y otros grupos, que se identifican por objetivos y tradiciones comunes a los grupos” (D’Ambrosio, 2001). La segunda se refiere a su etimología, centrada en que la Etnomatemática son las tics o ticas (modos, estilos, artes, ideas y técnicas de medir, calcular, comparar, contar y clasificar), de matemá (para explicar, aprender, conocer, lidear en/con, comprender fenómenos), en un determinado etno (ambientes naturales, sociales, culturales) (D’Ambrosio, 2014; Rosa & Orey, 2016). Se considera esencial que la Etnomatemática es “el área de investigación que estudia las multifacéticas relaciones e interconexiones entre ideas matemáticas y otros elementos culturales, como: la lengua, el arte, la artesanía, la construcción y la educación” (Gerdes, 2013).
En relación con las ticas, para Bishop (1999), existen seis actividades universales: contar, localizar, medir, diseñar, explicar y jugar, que estimulan procesos cognitivos de las personas y son relevantes tanto separadas como conectadas, para el desarrollo de ideas matemáticas en actividades cotidianas. En este sentido, contar se refiere a la manera sistemática de comparar y ordenar objetos diferenciados. Involucra el conteo corporal o digital, con marcas, uso de cuerdas u otros objetos para el registro, que dependerá del contexto de las personas donde se desarrolle esta actividad (Bishop, 1999).
Según Bishop (1999), la actividad de localizar, se refiere a la exploración del entorno espacial, conceptualización y simbolización de tal entorno con modelos, mapas, dibujos y otros recursos. En esta actividad, la postura geométrica juega un papel importante; son los tópicos relacionados con la orientación, la navegación, la astronomía, la geografía, aspectos topográficos y cartográficos del entorno. La actividad de medir es “importante para el desarrollo de las ideas matemáticas, y se ocupa de: comparar, ordenar y cuantificar cualidades que tienen valor e importancia” (Bishop, 1999). Cabe destacar que, el cuerpo humano fue el primer dispositivo que usó el hombre para medir, con unidades de medida, como: la cuarta, el paso, la braza, entre otras (Bishop, 1999).
Otra actividad universal es diseñar (Bishop, 1999), que se refiere a la abstracción de una forma de un entorno natural y cultural. Es decir, imponer una estructura específica o transformar una parte de la naturaleza por otra cosa u objeto, por ejemplo: arcilla, madera o terreno, y convertirlo en un artefacto, olla, mueble, entre otros. El diseño se refiere a la tecnología, los artefactos y objetos manufacturados que crean las personas, y usan para: el comercio, adornar, jugar y actividades religiosas, entre otras. Bishop (1999), destacó la actividad jugar, que “permite el desarrollo de ideas matemáticas, pues en los juegos emergen conexiones matemáticas con vistas culturales estrechamente vinculadas al orden, reglas, procedimientos, estrategias, repeticiones, ingenio, valores, a la interacción social y a la imaginación”. La actividad de explicar, se entiende como la indicación de los diversos aspectos cognitivos a investigar y conceptualizar el entorno y de compartir estas conceptualizaciones. Explicar eleva la cognición del ser humano para dar argumentos que estén por encima del nivel asociado a explicaciones basadas en la experiencia, dando respuestas a preguntas: ¿Cuántos?, ¿Dónde?, ¿Cómo?, Y principalmente la explicación es más abstracta al responder a la pregunta ¿Por qué? (Bishop, 1999).
Se destaca la reflexión de Aroca (2016), sobre la definición etimológica de la Etnomatemática, donde puntualiza que no es suficiente englobar e interpretar a todas las prácticas cotidianas existentes en las tics de mathema en una etno. Por tanto, manifiesta de manera inclusiva que la etnomatemática no sólo es lo sociocultural, también es lo político, lo ético, las relaciones que se promueven entre lo sociocultural y la educación, la economía de los pueblos y otros factores que emergen en las prácticas pedagógicas y didácticas, en la enseñanza y aprendizaje de las matemáticas. Incluir y relacionar aspectos culturales en el currículo de matemáticas, son “beneficios para los logros matemáticos de los estudiantes, ya que estos aspectos contribuyen a la percepción de que las matemáticas son parte de nuestra vida diaria y profundizan la comprensión de su naturaleza, al mejorar la capacidad de los estudiantes para hacer conexiones significativas” (Rosa & Gavarrete, 2016). Desde la perspectiva de Rosa y Orey (2018), el programa etnomatemática “enfatiza en la importancia de las comunidades en relación con el ambiente escolar, debido a que conecta la matemática con las prácticas culturales desarrolladas y utilizadas localmente”.
2.2 Conexión
Algunas investigaciones han estudiado las conexiones matemáticas con conceptos como la derivada (García-García & Dolores-Flores, 2020; Rodríguez-Nieto, Rodríguez-Vásquez & Font, 2020). Otros trabajos de etnomatemática enfatizaron en las conexiones, pero no entre conceptos geométricos (Madusise, 2015; Rosa & Orey, 2018; García-García & Bernandino-Silverio, 2019; Rodríguez-Nieto, 2020). Para los fines de esta investigación, una conexión se entiende como una relación verdadera entre dos ideas matemáticas A y B (Businskas, 2008). Por ejemplo, relacionar dos o más representaciones (simbólicas, gráficas), significados, o bien, usar fórmulas en procedimientos matemáticos para resolver un problema y relacionar conceptos matemáticos con algún objeto (e.g., los conceptos matemáticos que emergen en la elaboración de la tortilla), artefacto usado en prácticas cotidianas. Considerando las acepciones de etnomatemática propuestas por D’Ambrosio (2001; 2014), Gerdes (2013), Aroca (2016) y Rosa y Orey (2018), se reconoce que la etnomatemática relaciona los conocimientos de las personas que emergen en las prácticas cotidianas, con conceptos matemáticos institucionalizados: es decir, se hace referencia a conexiones etnomatemáticas.
2.3 Metodología
La investigación se desarrolló en tres etapas, bajo un enfoque cualitativo exploratorio (Hernández, Fernández & Baptista, 2014). i) Se seleccionó el participante y se procedió a la familiarización para conocerlo, comprender su realidad personal, familiar, laboral y cómo es su relación con las demás personas (Sandoval, 2002). ii) Se recolectaron los datos, a través de la aplicación de entrevista semiestructurada a un comerciante elaborador de tortillas. iii) Se analizaron los datos, considerando el método de análisis cualitativo propuesto por Hernández et al. (2014), de donde se obtuvo información para el reporte de los resultados de la investigación sobre las conexiones etnomatemáticas entre los conceptos geométricos.
Participante y contexto
El participante de esta investigación es un comerciante de tortillas, habitante de la ciudad de Chilpancingo de los Bravo, capital del estado de Guerrero, México. Él tiene aproximadamente cincuenta años de edad, y junto a su familia hace treinta años, se ha dedicado a comercializar productos de la canasta familiar. Es decir, su sustento diario depende de la venta de productos en una tienda y la venta de tortillas que él mismo elabora. El nivel máximo de estudios alcanzado por el comerciante es el universitario, ya que es graduado de enfermería.
Recolección de los datos
El autor de esta investigación se basó en la etnografía, donde se indagó acerca de la práctica cotidiana de un comerciante de tortillas. La etnografía (ethnos (pueblo, gente) y grapho (escritura, descripción)), permite la apropiación de la cultura de las personas y también reportar los sucesos tal y como se presentan en la realidad (Restrepo, 2016). Para lograr la explicación y participación del comerciante, se siguieron dos fases: i) se le solicitó participar en una entrevista a manera de acuerdo, para saber cómo se elabora la tortilla, y se le informó el objetivo del proyecto. El participante aceptó colaborar con la entrevista (acuerdo). Según Restrepo (2016), la etnografía “supone al etnógrafo como dispositivo de producción de conocimiento, lo cual no sucede impunemente. Esto significa que el principal medio de aprehensión, comprensión y comunicación que media la etnografía, es el etnógrafo y sus sensibilidades, habilidades y limitaciones”. En esta investigación, se adaptaron dos aspectos esenciales en la investigación etnográfica planteados por Restrepo (2016):
Aspecto 1: El investigador se dispone a vivir periodos de tiempo con la comunidad o la persona que desea estudiar, con el objetivo de conocer y apropiarse de los conocimientos, habilidades, historias de vida de la cultura (aquí se hace referencia al comerciante de tortilla).
Aspecto 2: Con el conocimiento recolectado y asimilado, el investigador o etnógrafo hace un reporte descriptivo donde explica los conocimientos de la actividad cultural estudiada.
En la fase 2 se aplicaron entrevistas semiestructuradas (Hernández et al., 2014), con el objetivo de colectar la información que sería suministrada por el comerciante durante la explicación sobre la elaboración de la tortilla. En este proceso, se usaron cámaras videograbadoras y notas de campo (se refiere al Aspecto 1).
Análisis de datos
El análisis de datos se realizó siguiendo el Aspecto 2 (Restrepo, 2016), donde se describieron los conocimientos aprendidos o adquiridos de la actividad cultural explorada (elaboración de la tortilla). La etnografía y la etnomatemática comparten principios metodológicos, dado que asumen hacer investigación con base en la descripción de grupos culturales. En este contexto, D’Ambrosio (2014), pone de manifiesto que una metodología para investigar en Etnomatemática es la capacidad de observación y análisis, donde se busca describir y comprender las prácticas de los grupos culturales. Asimismo, se realiza una observación de lo que se hace en algunas situaciones (reconocer acciones ad hoc).
En este caso, se reconoce que en los estudios etnográficos e incluso en las investigaciones en etnomatemáticas, se reportan resultados locales, es decir, focalizados en un solo grupo, cultura, artefacto o persona. Desde la perspectiva de Restrepo (2016), los estudios etnográficos giran en torno a descripciones y comprensiones situadas acerca de un cierto fenómeno de estudio, o bien, sobre las relaciones entre la práctica y los significados de las personas. Dichas “comprensiones situadas”, se refieren a las “formas de habitar e imaginar, de hacer y de significar el mundo para ciertas personas con las cuales se ha adelantado el estudio” (Restrepo, 2016).
El hecho de que las investigaciones etnográficas sean situadas, no quiere decir que solo se reporten los significados, características, modos de actuar, idioma, maneras de saber y hacer del objeto de estudio, sino que “se pueden establecer ciertas generalizaciones y teorizaciones, que van más allá de los sitios y gentes con las que se adelantó el estudio etnográfico” (Restrepo, 2016). Esto se hace en el presente estudio, ya que se exploran conocimientos específicos que emergen en la elaboración de la tortilla, pero se busca ampliar, relacionar y conectar dichos conocimientos de la vida cotidiana con aspectos matemáticos, los cuales no son considerados explícitamente por el comerciante entrevistado.
Para hacer el análisis de los datos, el investigador (I) consideró importante transcribir la entrevista y dejarla en forma de texto, y posteriormente, identificar e inferir los elementos matemáticos implícitos en el discurso del comerciante (P). En la transcripción se evidencian tres etapas de la elaboración de la tortilla. Este análisis detallado se presenta en la sección de resultados.
3. Resultados y discusión
3.1 Etapas de elaboración de la tortilla
Se han identificado tres etapas de elaboración de la tortilla, a saber: i) herramientas, ingredientes y obtención de la masa; ii) Obtención de la pelota de masa y uso de la prensa; y iii) Cuecer la tortilla (cocimiento, someter la tortilla a la acción del calor).
Etapa 1: herramientas, ingredientes y obtención de la masa
I. ¿En qué consiste la elaboración de la tortilla?
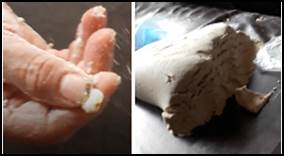
P. Los ingredientes que lleva, es el maíz, se pone a cocer, a hervir, luego se le pone cal para que se pele [pelar] el maíz, ya de ahí sale el maíz nixtamalizado, después se muele, y ya sale la masa (ver Figura 1).
I. Si, ¿Cuántos kilos de masa?
P. Son 20 kilos a 30 kilos.
En el extracto anterior, se observan los ingredientes usados para la elaboración de las tortillas, así como las herramientas, por ejemplo, el molino usado para moler el maíz (elote), y dejarlo en forma de masa. En la Figura 1 se muestra el grano de maíz nixtamalizado, donde el comerciante se refiere a quitarle el cuerito que cubre al maíz.
El proceso de nixtamalizar, se presenta detalladamente en el siguiente extracto de la transcripción:
I. ¿A qué se refiere con el nixtamalizado?
P. Se pone el bote con agua, se le pone… dependiendo de la cantidad de maíz, por ejemplo, para medio costal de maíz, que equivale a treinta litros, pongo medio de agua, medio costal de maíz (el costal trae 60 litros, medio son 30 litros) y le pongo de agua, la mitad de agua un bote y de ahí le pongo un litro de cal a esa agua y se revuelve bien, cuando ya está revuelto, se le echa el maíz.
I. ¿Cuánto de cal le coloca?
P. Un litro, una medida. Cuando ya pasa un tiempo más o menos de dos horas, cuando ya está el nixtamal, ya el maíz ya queda así (ver Figura 1), el maíz queda blanquito, el maíz trae un cuerito encima entonces ya con la cal le ayuda para que se pele.
I. Entonces, ¿nixtamalizar se refiere a qué?
P. A quitarle el pellejito al maíz, y ya de ahí esa es la seña de que ya está el nixtamal, por ejemplo, yo lo pongo hoy y el día de mañana lo saco, al lavarlo se le cae el cuerito, luego se muele en el molino y ya sale la masa, ese es el procedimiento del nixtamal.
En la explicación de la receta que sigue el comerciante, menciona que usa unidades de medida no convencionales de capacidad como el costal o saco que equivale a 60 litros (recipiente), es decir, se evidencian las actividades universales de medir y explicar con base en contenidos matemáticos.
Etapa 2: obtención de la pelota de masa y uso de la prensa
En la Figura 2, se presenta una pelota de masa, la cual es elaborada por el comerciante usando sus manos. En esta etapa, él mencionó que de la masa obtenida que oscila entre 20 a 30 kilos (medidas de masa) podrían salir entre doscientas y trescientas tortillas (conteos) (ver extracto de transcripción).
I. Y, ¿Cuántas tortillas salen de ahí?
P. Unas doscientas, trescientas tortillas. ¿Te pongo los tamaños? Este es un tamaño…
En la Figura 2 también se muestra el proceso de amasar la masa, hacer la pelota masa, ponerla en la prensa (localización), y luego, se le coloca el plástico para proteger la masa y aplanarla con la prensa. En tercer lugar se muestra un modelo de tortilla sin calentar (sin cuecer o calentar).
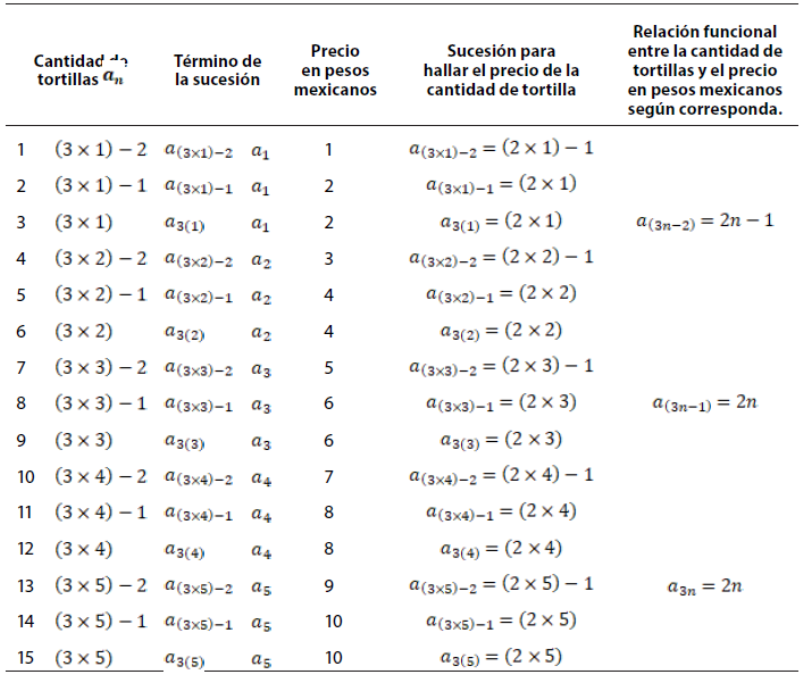
Además, el comerciante manifestó en su diálogo que él hace cinco tipos de tortillas (ver Figura 3), destacando su modo de uso, sus tamaños y grosor (ver el siguiente extracto de la transcripción).
I. Esa para qué sirve (tortilla mediana).
P. Esa es para taquitos de canasta, tacos de guisado (señala la Tortilla 2). Ésta es un poquito más grande, esta es para tacos dorados de pollo (señala la Tortilla 3), y ésta es otro poquito más grande, ésta es para el consumo para la comida (señala la Tortilla 4).
P. Otra tortilla es… esta es para los taquitos que les ponen la carne molida (Tortilla 1).
I. Y la tortilla, ¿solo tienen esta forma?
P. Si, solamente es la circular, y está otro moldecito que es para hacer los sopes, las picaditas, si te fijas es un poquito más gruesa (Tortilla 5), es para hacer los sopes que se le pone queso, crema, salsa y algún guisado si gustas.
I. Desde el momento que va a aplanar la masa, ¿tiene en cuenta que quede redonda la tortilla?
P. Si, pues…
I. ¿Qué le asegura a usted eso [redonda]?
P. Porque va en el centro… y como la prensa es redonda, pues lógico que tiene que salir…
I. Ah! porque la prensa es redonda le tiene que salir así…, Otra pregunta con relación al grueso…
P. Dependiendo del…, por ejemplo, para los sopes, es un grosor más o menos de un centímetro, no ha de ser… espérame voy a hacer una. Este es el grosor, será como la mitad de un centímetro (grosor de la tortilla 5).
I. ¿La mitad de un centímetro?
P. Sí, es la mitad de un centímetro.
I. Esa tiene de grueso medio centímetro ¿y las otras?
P. Son tortillas más delgadas…
I. ¿Cuánto?
P. Como dos milímetros.
I. Anteriormente, me clasificó las tortillas, para carne molida, para sope, para taquitos de pollo y para tacos dorados ¿tienen alguna relación con el grosor de la tortilla?
P. Si…, para los taquitos dorados la tortilla es lo más delgadita que se pueda.
I. ¿Cuánto?
P. Más o menos una décima y las otras son de dos milímetros.
En la Figura 4 se presentan las tortillas según su grosor.
En el anterior extracto de transcripción y en la Figura 4, el comerciante explica (actividad de explicar) ampliamente la clasificación de las tortillas en función del tamaño, forma circular (actividad universal de diseñar) y grosor que tienen medidas expresadas en centímetros y milímetros (actividad de medir).
Etapa 3: cuecer la tortilla
Por último, el comerciante lleva a cuecer las tortillas en el comal (ver Figura 5) para que queden suaves y dejarlas listas para el consumo de las personas.
Después de describir el proceso de elaboración de las tortillas, se consideró la transcripción de la entrevista, procediendo a identificar los elementos matemáticos implícitos en la forma de la tortilla, y las conexiones.
3.2 La tortilla: objeto para motivar el desarrollo de las conexiones entre conceptos de Circunferencia, Círculo y Cilindro
En la investigación basada en la etnografía, se sostiene que, “se pueden establecer ciertas generalizaciones y teorizaciones que van más allá de los sitios y gentes con las que se adelantó el estudio etnográfico” (Restrepo, 2016). En este caso, se considera que el comerciante tiene una idea acerca de la forma de la tortilla, por ejemplo, reconoce que es circular (ver el siguiente extracto de transcripción):
I. La tortilla, ¿Solo tienen esta forma?
P. Si, solamente es la circular…
Pero, existen otros factores que son propios de las matemáticas, específicamente de la geometría, como: las relaciones entre la circunferencia y el círculo, diámetro, radio, área, perímetro, entre otros aspectos matemáticos que se reportan en esta investigación, como se ejemplifica en la Tabla 1 y en las Figuras 6 a 10. Esto no quiere decir que el comerciante debe saber los conceptos geométricos obligatoriamente, sino que él los usa desde su experiencia, mencionando la forma y tamaño de la tortilla, y el investigador reconoce la matemática implícita. En la Tabla 1 se muestra el uso del centímetro, que también es utilizado por el comerciante.
Tabla 1 Tamaños de las tortillas, características y conexiones.

Nota. Se usó la regla para medir el diámetro de cada tortilla.
El comerciante usa una prensa con superficies planas de forma circular, con 19 cm de diámetro, entonces, el área de la superficie es de 90.25 π cm 2 y su perímetro es de 19 π cm (ver Figura 11).
Otras conexiones etnomatemáticas se manifiestan si se considera el área de la base de la tortilla con forma de cilindro, como una función del radio A(r) = πr 2 , donde se observa que cuando el radio varía, el área de cada una de las tortillas también varía (aumenta o disminuye). Además, otra conexión que se establece a partir de las tortillas, es que si derivamos la función A(r) = πr 2 con respecto al radio (A’(r) = πr), se obtendrá el perímetro de la circunferencia para cada tipo de tortilla. Por ejemplo, el área de la tortilla 1 es A(5.75cm) = π(5.75cm) 2 = 33,062πcm 2 y el perímetro se halla usando la derivada A’(5.75cm) = 2π(5.75cm)=11.5 πcm. De igual manera se halla el área y el perímetro de todas las áreas de las tortillas cuyos resultados coinciden con los presentados en la Tabla 1, pero se pueden establecer relaciones, donde el área de la superficie circular de la tortilla 4 es aproximadamente el doble del área de la tortilla 1. En este contexto, se establecen conexiones entre el círculo y la circunferencia, y se conectan otros conceptos como función, derivada, área, perímetro, radio, entre otros.
3.3 Conexiones entre la razón de la circunferencia y el diámetro en cada círculo
Existe una relación entre la longitud de la circunferencia y el diámetro del círculo, donde se evidencia la conexión de dos conceptos geométricos por medio de un número irracional pi (π), ver Tabla 2.
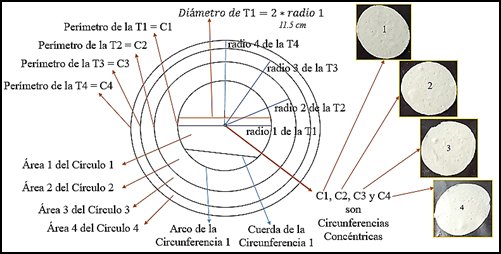
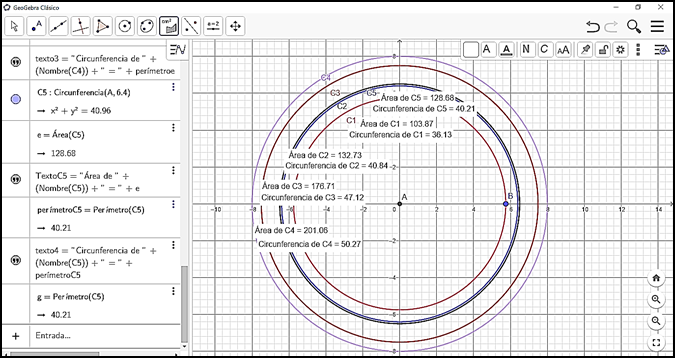
En la Figura 12, se sintetiza y se señalan algunas partes de la circunferencia y el círculo relacionadas con la tortilla, para establecer las conexiones etnomatemáticas entre éstos conceptos.
Además, en la Figura 12 se identifica otra conexión entre las circunferencias, por ejemplo, se observa que C1, C2, C3 y C4, comparten el mismo centro, entonces, se les denomina concéntricas.
3.4 Conexiones entre la cantidad de tortillas y el precio
En la información suministrada por el comerciante acerca de los precios de las tortillas, se identificaron relaciones funcionales entre la cantidad de tortillas y el precio al momento de comercializarlas. En este sentido, considerando los tipos de tortillas de la Tabla 1, la venta de la tortilla 1 se modela como se muestra en la Tabla 3 y en el extracto de la transcripción.
I. ¿Cuál es el precio de la tortilla pequeña?
P. La tortilla chiquita vale cincuenta centavos… que vienen siendo cuatro tortillas por dos pesos, ya nada más se cobra porque la chiquita da un poquito más de trabajo.
En el caso de las tortillas 2, 3 y 4 de la Tabla 1, se evidenció que el comerciante usa implícitamente una sucesión compuesta que implica progresiones aritméticas de orden uno en los números naturales, cuyo patrón de referencia es la venta de tres tortillas por dos pesos, que le permite relacionar cualquier cantidad de tortillas con el precio de venta (ver Tablas 4 y 5). Cabe destacar que, por una tortilla el comerciante cobra un peso, por dos tortillas cobra dos pesos y por quince tortillas cobra diez pesos (ver extracto de la transcripción).
I. Ya la otra (Tortilla 4) son tres piezas por dos pesos, o sea, una tortilla grande…
P. A un peso, luego, ya la que le sigue…
I. ¿La mediana?
P. Tres por dos pesos y una te cuesta un peso.
I. Y, ¿Si vienen por dos tortillas?
P. Serían dos pesos en realidad conviene más. Hay personas que dicen yo nada más quiero dos tortillas y le decimos te conviene más las tres, pero dicen nada más necesito dos y se les cobra dos pesos.
I. ¿Cinco tortillas?
P. Cuatro pesos.
I. Y, ¿Cuatro tortillas?
P. Tres pesos, nueve tortillas seis pesos.
I. ¿Por qué seis pesos?
P. Porque son tres (tortillas) por dos (pesos) (patrón de referencia), son tres, seis, nueve; son tres por dos.
I. Y en conjunto o grupo ¿A cómo las venden?
P. Son quince tortillas por diez pesos, siete tortillas por cinco pesos, treinta tortillas por veinte pesos, diez tortillas por diez pesos.
En la Tabla 5, se analiza el comportamiento de la secuencia del precio de la tortilla en pesos mexicanos con respecto a la cantidad de tortillas. En esta secuencia se identificaron tres progresiones aritméticas crecientes, que constituyen una sucesión numérica compuesta, es decir, tres sucesiones intercaladas. Por ejemplo, la primera sucesión (azul) viene dada por el término k-ésimo (cantidad de tortillas) α (3n-2) = 1, 4, 7, 10, 13,…, generalizados a partir de la regla 2n - 1. La segunda sucesión (amarillo) se conforma por el término k-ésimo α (3n-1) = 2, 5, 8, 11, 14,…, generalizados a partir de la regla 2n. La tercera sucesión (naranja) se comporta siguiendo el términos k-ésimo α3n = 3, 6, 9, 12, 15,…, con la regla general 2n, y, para identificar esta sucesión fue esencial tener en cuenta el patrón de referencia mencionado por el comerciante refiriéndose a tres tortillas por dos pesos.
Se considera que al modelar la situación sobre la relación cantidad de tortillas y sus precios, se evidencia matemáticamente una sucesión compuesta, entendida como aquella sucesión que incluye dos o más sucesiones intercaladas, que pueden ser figurales o numéricas. Cada sucesión tiene una regla diferente, o bien, en este análisis se observan dos sucesiones que comparten la misma regla pero con términos k-ésimos diferentes. En el caso de la tortilla 5, cada unidad cuesta dos pesos mexicanos, y esta situación se modela como se presenta en la Tabla 6 y en el extracto de transcripción.
Tabla 6 Relación funcional entre la cantidad de la tortillas 5 y el precio.
| Cantidad de tortillas 5 (m) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | … | p(m) = 2m |
| Precio en pesos mexicanos p(m) | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | … |
I. ¿Cuánto vale una tortilla para sope?
P. Esa te cuesta dos pesos, es más gruesa.
I. y ¿En cantidad?
P. Es al mismo precio, se sigue dando igual.
En el análisis realizado también se pueden establecer relaciones de equivalencia entre los precios de las tortillas, por ejemplo, el precio de dos tortillas 1 es equivalente al precio de una tortilla 3. El precio de cuatro tortillas 1 es equivalente al precio de una tortilla 5, o bien, el precio de dos tortillas 3 es equivalente al precio de una tortilla 5.
Por otra parte, se le preguntó al comerciante que si vendía las tortillas por kilogramo, el respondió que sí, que traía veintisiete tortillas y costaba dieciocho pesos (ver el extracto de la transcripción).
I. Si tenemos que veintisiete tortillas de las grandes trae un kilo, vendiéndolas como usted lo hace a tres por dos, ¿Cuánto cobraría?
P. Dieciocho pesos.
I. ¿Por qué?
P. Porque primero dieciocho cuesta el kilo y son tres tortillas por dos pesos y son veintisiete tortillas por un kilo, ya serían quince tortillas por diez más doce tortillas por ocho pesos ya equivale a veintisiete tortillas, en pesos ya serían dieciocho pesos, sería lo mismo en dinero y en cantidad de tortillas.
En este sentido, si veintisiete tortillas equivalen a un kilogramo (convertidos a 1000 gramos), entonces ¿A cuántos kilogramos equivale una tortilla?, equivale a 37.03 gramos aproximadamente. Ahora bien, relacionando ésta información con el volumen de la tortilla 4 (grande) presentada en la Tabla 1, se obtienen las conexiones entre cantidad de tortillas, kilogramos y volumen (ver Tabla 7).
En relación con la masa, el comerciante mencionó que una tortilla 4 grande es equivalente a una tortilla 5, y con la cantidad de masa de una tortilla 4 se pueden hacer tres tortillas 1; es decir, 1 tortilla grande = 3 tortillas pequeñas y 1/3 de una tortilla grande = 1 tortilla pequeña (ver extracto de transcripción). El comerciante no vende la tortilla pequeña por kilogramos porque es más laboriosa.
P. Con la masa de una tortilla grande 4 ya en pequeña (tortilla 1) son tres tortillas.
I. ¿Cuántas tortillas para sopes salen de la tortilla grande?
P. Para el sope es la misma masa de la grande (tortilla 4), pero el sope es un poquito más grueso.
I. Para el sope ¿lo presiona menos?
P. Si, para que te salgan gorditas, es la misma masa, nada más que no se apachurra mucho.
3.5 Conexiones entre el círculo, la circunferencia y el cilindro, usando GeoGebra
Para profundizar en el análisis de las conexiones etnomatemáticas entre conceptos geométricos, es importante considerar los cinco tamaños de las tortillas identificados a través de la etnografía, teniendo en cuenta los diámetros y radios como una alternativa didáctica, con la ayuda del Software GeoGebra. Esto permite innovar y dinamizar las relaciones desencadenadas a partir de la tortilla, con el propósito de darle más herramientas a los estudiantes y profesores de matemáticas para el desarrollo de conceptos como: circunferencia, círculo y cilindro, y medidas de perímetro, área y volumen.
Construcción de la circunferencia y el círculo con GeoGebra
Se explican las conexiones entre la circunferencia y el círculo por medio de GeoGebra. Una vez que el profesor o el estudiante hayan explorado las relaciones que emergen con el objeto tortilla usando lápiz, papel, regla y compás, puede conectarse con el entorno digital. Fuentes (2012), usó el software Cabri para el tratamiento de simetrías, traslaciones, rotaciones, áreas, etc., evidenciadas en artesanías. También, en Bandeira Bezerra y Lanner de Moura (2018), se usó el programa Corel Draw para la construcción del arco y la flecha (objeto cultural), donde notaron características como medida de ángulos, sector circular, cálculo de área, entre otros. A continuación, se presentan algunas alternativas didácticas fundamentadas en la etnomatemática y visualizadas en GeoGebra, las cuales emergen de la elaboración de la tortilla.
i) Construcción de las circunferencias (Tortillas: C1=T1, C2=T2, C3=T3, C4=T4 y C5=T5)
Para la construcción de la circunferencia en GeoGebra, se consideraron las medidas de los radios de las tortillas que se habían medido con una regla y se construyeron suponiendo un entorno a papel, lápiz, regla y compás. Después, se eligió la herramienta Circunferencia: centro y radio; luego, se ubicó el centro en el punto A (0, 0) y se insertó el radio = 8cm para el caso de C4. Una vez obtenida la representación gráfica de la circunferencia, se usó la herramienta Área para hallar el área del círculo, la cual dio como resultado Área de C4 = 201.06 cm 2. Por último, por medio de la herramienta Distancia, se determinó el perímetro o la longitud de la circunferencia C4 = 50.27 cm. Para la construcción de las circunferencias C1, C2, C3 y C5 se consideró el mismo procedimiento (ver Figura 13). Al proceso de construcción de la circunferencia se le denomina una conexión procedimental, dado que a partir de herramientas y fórmulas se llega a su representación gráfica.
En la Figura 13, se evidencia que la conexión entre el círculo y la circunferencia depende del radio, dado que este es útil para obtener el área y el perímetro. Por otra parte, se reconoce la conexión permanente entre representaciones gráficas y simbólicas, dado que GeoGebra permite trabajar con las vistas algebraica-simbólica y gráfica. Además, las circunferencias construidas comparten un mismo centro A (0, 0), permitiendo denominarlas circunferencias concéntricas.
ii) Hallar el área de la corona circular formada por circunferencias concéntricas
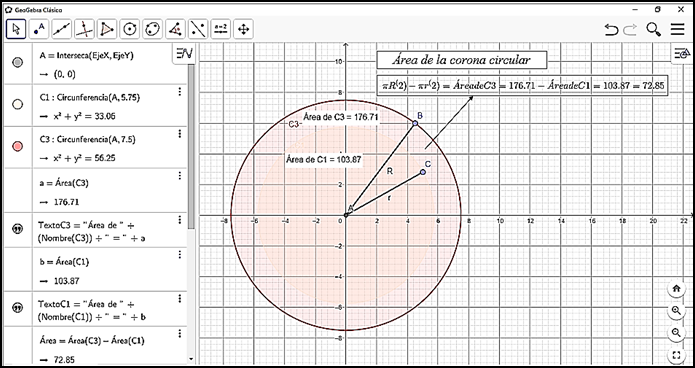
Se considera importante abordar el tema de la corona circular, que es la región comprendida entre dos círculos concéntricos, es decir, que comparten el mismo centro. Se enfatiza en la corona circular o anillo, porque se pueden tomar dos tipos de tortillas que tengan radios diferentes y hallar el área de dicha región. En este sentido, el área de la corona circular de radios R (mayor) y r (menor) es igual al producto de π por la diferencia de los cuadrados de dichos radios, o bien, la diferencia de áreas de los dos círculos concéntricos (A = π(R 2-r 2)). En la Figura 14 por medio de GeoGebra, se presenta la construcción de las circunferencias concéntricas C1 y C3 y el área de la corona circular, la cual se determinó insertando el comando a - b en la entrada de la vista algebraica de GeoGebra.
En la Figura 14 se muestra que el área de la corona circular se puede hallar de otra manera, a través de una fórmula y considerando las áreas de los círculos delimitados por las circunferencias C3 (a=Área C3 = 176.71 cm 2) y C1 (b= Área C1 = 103.87 cm 2): primero se selecciona la herramienta Texto, luego se le da clic en Avanzado, se elige la opción Fórmula LaTex y por último se inserta la siguiente fórmula: (πR^(2)- πr^(2)) = a-b = Área), teniendo en cuenta que la palabra Área vincula a la fórmula introducida con el término Área ubicado en la vista algebraica con valor 72.85 cm 2.
3.6 Conexión entre el círculo, la circunferencia y el cilindro
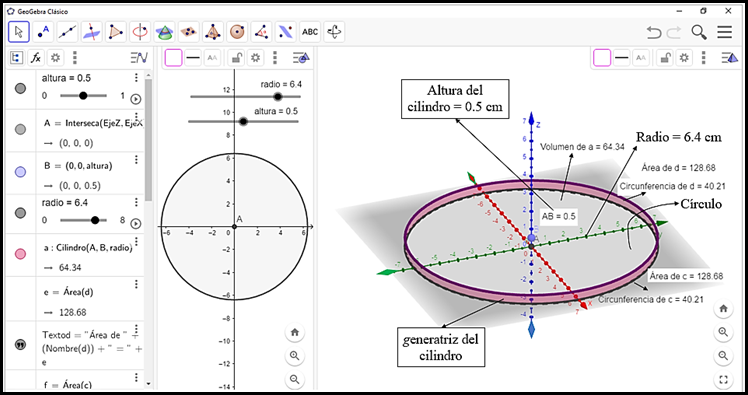
Otras conexiones pueden emerger en la construcción de la tortilla, representada como un cilindro en el software GeoGebra. Por ejemplo, en la Figura 15 se construyó un cilindro donde se tuvieron en cuenta las medidas del radio (r = 6.4 cm) y del grosor (altura = 0.5 cm), correspondientes a la tortilla 5. Para esta construcción se debe seleccionar una vista gráfica en tercera dimensión (3D). Posteriormente, se ubica un punto A (0, 0, 0) en el plano tridimensional y, luego, se selecciona la herramienta cilindro teniendo en cuenta los puntos A y B (que representa la altura), el cual lleva asociado un deslizador llamado radio. Luego que se haya obtenido el cilindro, se inserta otro deslizador denominado altura y se vincula con el punto B = (0, 0, altura) (insertado en la entrada de la vista algebraica). Una vez se tuvo el cilindro con r = 6.4 cm y altura = 0.5 cm, se procedió a determinar las áreas de los círculos (bases del cilindro), los perímetros de las circunferencia asociadas a las bases, la altura del segmento AB y por último, el volumen del cilindro que representa a la tortilla 5. Cabe destacar que, usando los deslizadores, se pueden modificar las medidas del radio y la altura y conseguir las áreas y los volúmenes de los otros tipos de tortillas.
Las medidas evidenciadas en la Figura 15, correspondientes al área, perímetro, volumen, entre otros, son similares a las halladas en un entorno a papel, regla, lápiz y compás.
De forma general, en este trabajo se identificaron las conexiones etnomatemáticas entre el círculo, la circunferencia y el cilindro que emergen en la práctica cotidiana de la elaboración de la tortilla, destacándose que para hallar el área y el perímetro hay dos elementos principales (el radio y π) que se conectan para conseguir dichas medidas. Además, se considera importante que, para hallar el volumen del cilindro es necesario el área de la base, es decir, existe una conexión entre conceptos y a la vez se vislumbra una conexión de procedimiento, por ejemplo, el procedimiento 1 es cuando se halla el área del círculo y el procedimiento 2 se evidencia cuando se halla el volumen usando la fórmula: V = πr 2 g, considerando como requisito el área de la base. Otras conexiones se evidenciaron entre representaciones diferentes, en particular las relaciones entre las representaciones gráficas de la circunferencia, círculo y cilindro, y sus respectivas representaciones simbólicas-algebraicas (contenidas en los procedimientos para hallar el área, perímetro y volumen). Este tipo de representaciones se evidenciaron en el trabajo con GeoGebra, ya que permite hacer representaciones algebraicas, gráficas y simbólicas de los objetos matemáticos simultáneamente.
También se analizaron situaciones matemáticas donde la tortilla puede usarse como objeto motivador, material concreto que permite establecer conexiones etnomatemáticas dado que relaciona un contexto cotidiano con conceptos matemáticos. Es importante que los profesores y estudiantes reconozcan que con la tortilla, se pueden trabajar la circunferencia, el círculo, el cilindro, hallar medidas de áreas, volumen, perímetro, así como el tratamiento de circunferencias concéntricas, área de coronas circulares, áreas laterales y totales. Mientras que, en otras investigaciones centradas en la tortilla, por ejemplo, se han preocupado más por indagar acerca del impacto del precio de la tortilla en los hogares (López et al., 2015), caracterización de los consumidores de tortilla (Espejel-García et al., 2016), y generación de ingresos económicos (Rodríguez et al., 2017).
Las investigaciones en etnomatemática realizadas en México, se han interesado en el análisis de artefactos (García-García & Bernandino-Silverio, 2019), medidas no convencionales (Ávila, 2014; Rodríguez-Nieto et al., 2017), cálculo aritmético (Palacio, 2019). También han trabajado sobre cómo los profesores de las escuelas indígenas integran la etnomatemática en sus clases de matemáticas (Ávila, 2014). Ante esta situación, se considera que los resultados reportados son un aporte a la investigación y a los sectores educativo y sociocultural. Después de hacer el análisis de las conexiones entre conceptos geométricos, se evidenció que entre la cantidad de tortillas y los precios, emergen conexiones entre sucesiones compuestas que modelan las situaciones para el tipo de tortillas 3, y relaciones funcionales para el caso de las tortillas 1 y 5. Cabe destacar que, la sucesiones compuestas pueden desarrollarse desde la educación primaria, por ejemplo, en México aparecen en cuatro grado (Secretaría de Educación Pública [SEP], 2014).
En la Figura 16 se presenta la conexión entre el contexto sociocultural mexicano, la tortilla y la matemática, donde se muestra que en todos los estados de México consumen la tortilla. No obstante, en este trabajo se ofrece una vista más amplia con un sentido etnomatemático, donde se resalta la conexión entre la tortilla y algunos conceptos matemáticos que pueden trabajarse a partir de ella.
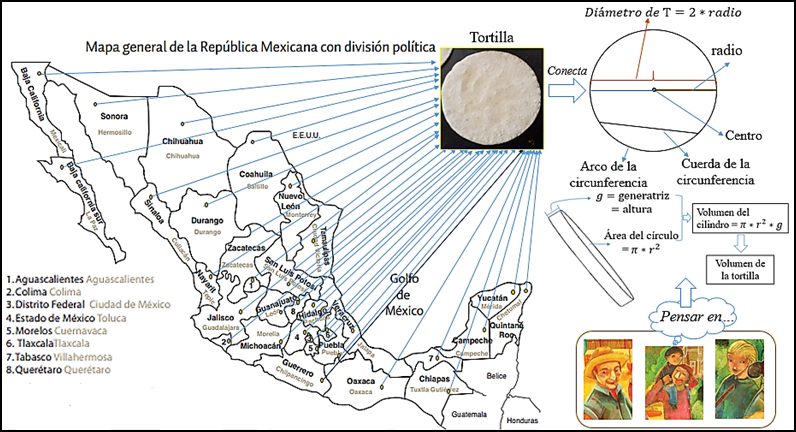
Elaboración propia con base en la información tomada de Recillas, Morales y Pedroza (2008).
Figura 16 Conexión etnomatemática: contexto sociocultural-tortilla-matemática institucionalizada
4. Conclusiones
En este artículo se propone que los mexicanos (niños, jóvenes y adultos) y extranjeros, reconozcan que en la forma de la tortilla se evidencian conceptos como la circunferencia, el círculo, el cilindro, donde se pueden trabajar temáticas sobre el área del círculo, perímetro de la circunferencia, volumen del cilindro, entre otros. De esta manera, se comparte la perspectiva de Laurens et al. (2019), cuando afirmaron que, aprender a usar la cultura local les da a los estudiantes valor para reconocer y apreciar su cultura. Se reflexiona que, conectar el conocimiento geométrico explorado en este artículo con el currículo y los libros de texto de matemáticas, podría favorecer a la enseñanza de conceptos geométricos, mediciones, conteos y sucesiones numéricas compuestas (SEP, 2014).
En futuras investigaciones, se sugiere usar los conocimientos etnomatemáticos identificados en este trabajo, en el diseño de tareas extramatemáticas y en el proceso de enseñanza y aprendizaje de la geometría, considerando las conexiones entre los conceptos: circunferencia, círculo y cilindro. Además, se podrían crear e implementar actividades interactivas con GeoGebra mediadas por plataformas virtuales, que involucren tareas que promuevan las conexiones entre conceptos geométricos, en el contexto de la elaboración de tortillas.