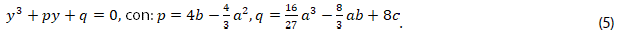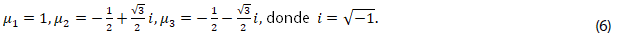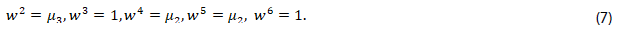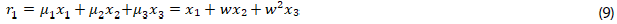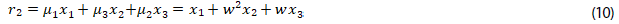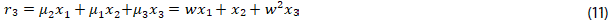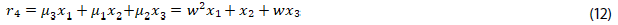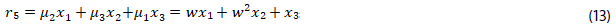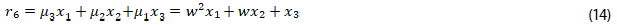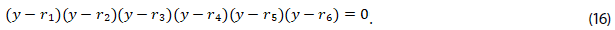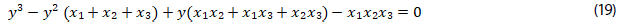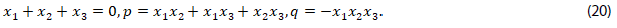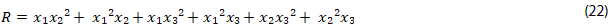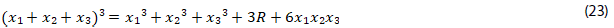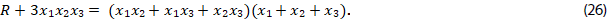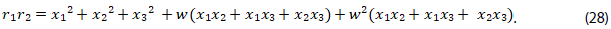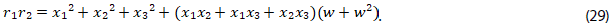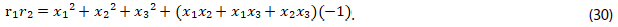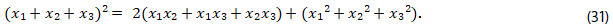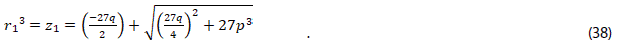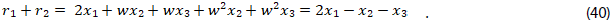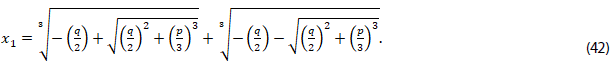1. Introducción
En la investigación sobre la Didáctica de las Matemáticas, se considera relevante el estudio de las conexiones matemáticas (Rodríguez-Nieto, Rodríguez-Vásquez & Font, 2020). Los resultados de estas investigaciones, han generado un cierto consenso sobre la necesidad de incorporar en los currículos de matemáticas procesos de conexión al interior de ella y con la vida cotidiana. La relevancia que se otorga al establecimiento de conexiones matemáticas, está relacionada con la importancia que se da a la reflexión sobre la complejidad de los objetos matemáticos (y su articulación) en casi todos los marcos teóricos de la Didáctica de la Matemática. En particular, en el Enfoque Ontosemiótico de la Cognición e Instrucción matemática (en adelante EOS) (Godino, Batanero & Font, 2007; 2019), se modeliza la complejidad de los objetos matemáticos por medio de sus significados parciales, y se considera que el estudio de los diferentes significados de un objeto matemático, es un tema relevante de investigación para la Didáctica de las Matemáticas.
Recientemente se han propuesto diferentes modelos de categorías de conocimientos y competencias del profesor de matemáticas. Entre ellos, el Modelo de Conocimientos y Competencias Didáctico Matemáticas (CCDM), basado en constructos del EOS (Godino, Giacomone, Batanero & Font, 2017; Pino-Fan, Breda & Font, 2017). En este modelo se considera que, para que un alumno pueda ser competente en la aplicación de las nociones matemáticas, es necesario que en el proceso de instrucción se le enseñe una muestra representativa de los diferentes significados parciales (o sentidos), de estas nociones. En consecuencia, se considera necesario que los profesores de matemáticas tengan en cuenta la complejidad del objeto matemático que se pretende enseñar (entendida ésta como pluralidad de significados), en el diseño, implementación, valoración y rediseño de procesos de instrucción. Por tanto, son necesarios procesos formativos que permitan a los profesores reflexionar sobre la complejidad de los objetos matemáticos (en términos de pluri significados), y su posible aplicación en su práctica docente con la finalidad de mejorarla (Calle & Breda, 2019; Calle, Breda & Font, 2020; Esqué & Breda, 2021; Font, Breda & Seckel, 2017).
A su vez, en el EOS, los significados parciales se modelizan en términos de prácticas matemáticas y de las configuraciones de objetos primarios que las activan. Para la realización de una práctica matemática y para la interpretación de sus resultados como satisfactorios, se necesita poner en funcionamiento determinados objetos matemáticos. Si consideramos, por ejemplo, los objetos que están participando en la realización y evaluación de la práctica que permite resolver una situación-problema, vemos el uso de lenguajes, verbales, algebraicos, gráficos y numéricos. Estos lenguajes son la parte ostensiva de una serie de conceptos, proposiciones y procedimientos, que intervienen en la elaboración de argumentos para decidir si las acciones simples que componen la práctica, y ella, en tanto acción compuesta, son satisfactorias. En consecuencia, cuando un agente (institución o persona), realiza y evalúa una práctica matemática, activa un conjunto formado por problemas, notaciones, definiciones, proposiciones, procedimientos y argumentos. Los objetos primarios están relacionados entre sí formando configuraciones, definidas como las redes de objetos intervinientes y emergentes de los sistemas de prácticas. Estas configuraciones pueden ser epistémicas (redes de objetos institucionales), o cognitivas (redes de objetos personales).
En el presente artículo se aborda la siguiente pregunta: ¿Cuáles son los significados del objeto grupo? O ¿qué es el objeto grupo? Este problema, de tipo epistémico, se relaciona con el siguiente problema cognitivo: ¿qué significa un objeto grupo para un estudiante o para el profesor en un contexto institucional determinado?
En este sentido, se presenta la reconstrucción del significado global del objeto Grupo (Sepúlveda, 2015; 2017; 2018), que consiste en identificar los sistemas de prácticas matemáticas que van asociados a configuraciones epistémicas, de donde emergen significados parciales para cada tipo de situación reconstruida, la que a su bez se usa como referente para elaborar los significados que se pretenden incluir en los currículos de una institución de enseñanza concreta (Godino, 2009). Este hecho adquiere importancia porque, a partir de ellos, el profesor, como representante de la institución educativa, determina cuál o cuáles serán los significados pretendidos, implementados y los evaluados en los procesos de instrucción, buscando lograr la comprensión del objeto matemático (Pino-Fan, 2013).
El significado global de referencia de un objeto matemático, se define a partir de dos conceptos: el global y el de referencia, que se identifican tanto en los libros texto como en los currículos (Pino-Fan, Godino & Font, 2011).
Al respecto, en el documento se da respuesta a las siguientes preguntas: ¿De qué forma se relacionan las configuraciones epistémicas del objeto matemático Grupo?, ¿Es posible generar nuevas configuraciones epistémico-didácticas, como alternativas para la enseñanza de nociones de Teoría de Grupos?, ¿Qué representatividad tienen los significados de referencia del objeto matemático en los libros de texto de Teoría de Grupos, teniendo como referente el significado global del objeto? (Pino - Fan, 2017).
Para dar respuesta a algunos de los anteriores interrogantes, se realizó una investigación exploratoria - descriptiva, con un enfoque cualitativo. Entre los resultados del estudio, se abordan: la complejidad para la enseñanza y el aprendizaje de la estructura Grupo, desde las primeras concepciones en la resolución de ecuaciones algebraicas hasta la emergencia del significado abstracto; seis situaciones problemas que motivaron el desarrollo histórico del objeto: 32 configuraciones epistémicas y los significados parciales identificados en los problemas (Sepúlveda, 2015; 2017; 2018). También se incluyen: configuraciones epistémico-didácticas; diseño de situaciones didácticas para resolver la ecuación algebraica de grado tres por el método de Lagrange para promover la emergencia de los grupos Z 3 y S 3 y la valoración de la representatividad de los significados de referencia en los libros de texto de Teoría de Grupos.
2. Marco teórico y metodológico
En esta investigación se utilizó el EOS, desarrollado en diversos trabajos por Godino y colaboradores (Godino, Batanero & Font, 2007; 2019). En estos trabajos, se evidencia el desarrollo de un modelo epistemológico para las matemáticas, con bases antropológicas y socioculturales; un modelo cognitivo, con bases semióticas de índole pragmatista; y un modelo instruccional que precisa nociones teóricas desarrolladas y adaptadas de otras teorías que integran este enfoque, las cuales se constituyen en herramientas teóricas y metodológicas necesarias para el desarrollo de la investigación en Educación Matemática y en la misma Matemática (Godino, 2012; Font, Godino & Gallardo, 2013). A nivel internacional, este enfoque se reconoce como modelo teórico modular e inclusivo dentro de la Didáctica de las Matemáticas (Presmeg, 2014; Kaiber, Lemos y Pino-Fan, 2017).
En el EOS, la noción de sistema de prácticas juega un rol fundamental, tanto desde la perspectiva epistemológica como desde la perspectiva didáctica. El sistema de prácticas, es “toda actuación o manifestación (lingüística o no) realizada por alguien para resolver problemas matemáticos, comunicar a otros la solución, validar la solución y generalizarla a otros contextos y problemas” (Godino & Batanero, 1994, p. 334). Estas prácticas pueden ser llevadas a cabo por una persona (sistema de prácticas personales), o compartidas dentro de una institución (sistema de prácticas institucionales).
De los sistemas de prácticas matemáticas operativas y discursivas, emergen nuevos objetos que provienen de las mismas y dan cuenta de su organización y estructura. Cuando un agente realiza y evalúa una práctica matemática, activa un conglomerado de entidades básicas u objetos matemáticos primarios, a saber: situaciones-problemas, elementos lingüísticos, conceptos, proposiciones, procedimientos y argumentos. Las situaciones-problemas son el origen o razón de ser de la actividad; con el lenguaje se representa las restantes entidades y sirve de instrumento para la acción; los argumentos justifican los procedimientos y proposiciones que relacionan los conceptos entre sí. Estos objetos matemáticos primarios, se articulan formando la configuración de objetos. Estas configuraciones pueden ser epistémicas (redes de objetos institucionales) o cognitivas (redes de objetos personales), según si los objetos matemáticos primarios se ponen en juego en prácticas institucionales o personales, respectivamente.
En el EOS, se asume el postulado antropológico de la relatividad socioepistémica, tanto de los sistemas de prácticas como de los objetos emergentes de ellas y sus significados. Así, cuando preguntamos: ¿qué es el objeto matemático Grupo? y en general, ¿Cuál es el significado de un objeto matemático concreto? desde el EOS se propone como respuesta: Es el sistema de prácticas que realiza una persona (significado personal), o compartidas en el seno de una institución (significado institucional), para resolver un tipo de situaciones-problemas.
En esta dirección, el estudio de los significados de la estructura Grupo, se realizó a nivel exploratorio-descriptivo de tipo documental, con el objetivo de caracterizar los significados más relevantes en la emergencia de esta estructura matemática. Para esto, se analizaron las problemáticas abordadas por algunos matemáticos en diversas épocas de la historia, y se determinaron las configuraciones epistémicas, emergentes de las problemáticas (estudio epistemológico, histórico y fenomenológico). Posteriormente, se realizó el análisis semiótico a cuatro libros de texto, para determinar los significados institucionales pretendidos y la representatividad respecto al significado holístico de referencia (Pino-Fan, Godino & Font, 2011) del objeto grupo. Finalmente, se retoma una situación problema y se evidencia la emergencia de dos significados parciales de la estructura grupo: Grupo de permutaciones y Grupo de los enteros módulo n.
3. Resultados y discusión
3.1 Significados de referencia de la estructura Grupo
Emergencia de los significados parciales de Grupo
En el estudio fenomenológico, histórico, epistemológico sobre la emergencia de los significados parciales de Grupo, se identificaron los siguientes cinco periodos, caracterizados por problemas específicos, con los respectivos sistemas de prácticas y configuraciones epistémicas de objetos matemáticos primarios (Sepúlveda, 2015; 2018), ver tablas 1 a 4.
Tabla 1 Sistemas de prácticas para resolver los problemas SP0.
| Prácticas Matemáticas (CE) | Situación problema (SP) | Significado parcial (SIP) |
|---|---|---|
| CE0. Ecuaciones algebraicas particulares de grado uno, dos, tres y cuatro. | SP0. Resolver ecuaciones algebraicas de grado uno, dos, tres y cuatro, para casos particulares. | SIP0. Métodos empíricos de solución de ecuaciones algebraicas particulares de grado uno, dos, tres y cuatro. |
| CE0.1: Las ecuaciones lineales en la matemática egipcia.(siglo XVII A.C.). | SP0.1: Resolver ecuaciones algebraicas de grado uno y dos. | SIP0.1: Método de la falsa posición para resolver ecuaciones de grado uno y dos. |
| CE0.2: Distribución de un área en cuadrados en la matemática egipcia. | SP0.2: Resolver ecuaciones que modelan la distribución de un área en cuadrados. | SIP0.2: Método para resolver una ecuación de grado dos por los egipcios. |
| CE0.3: Ecuaciones algebraicas de grado dos y tres, en la matemática Babilónica. (1800 al 1600 A.C.). | SP0.3: Resolver ecuaciones algebraicas de grado dos y tres. | SIP0.3: Método para resolver ecuaciones algebraicas de grado dos y tres por los babilonios. |
| CEO.4: Ecuaciones algebraicas de grado dos en la cultura griega | SP0.4: Resolver la ecuación algebraica de grado dos. | SIP0.4: Método para resolver una ecuación algebraica de grado dos por los griegos. |
| CE0.5. Ecuaciones algebraicas de grado 1 y 2 en la cultura Hindú. (500 - 1200 D.C). | SP0.5: Resolver ecuaciones algebraicas de grado uno y dos. | SIP0.5: Método de los hindúes para la solución de ecuaciones algebraicas de grado 1 y 2 |
| CE0.6: Ecuaciones de grado dos en la cultura Árabe. (825D.C.). | SP0.6: Resolver ecuaciones algebraicas de grado dos. | SIP0.6: Método de los árabes para solucionar ecuaciones de segundo grado. |
| CE0.7: Ecuaciones de grado 2 por propiedades de los números cuadrados. | SP0.7: Resolver ecuaciones algebraicas de grado dos | SIP0.7: Método Fibonacci de los cuadrados para resolver ecuaciones de grado 2. |
| CE0.8: Ecuaciones de grado 3. | SP0.8: Resolver ecuaciones algebraicas de grado tres. | SIP0.8: Método de Fibonacci para resolver ecuaciones de tercer grado |
| CEO.9: Caso especial de la ecuación cúbica. Del Ferro (1500) | SP0.9: Resolver un caso particular de la ecuación cúbica. | SIP0.9: Método Del Ferro para resolver la ecuación cúbica, caso especial. |
| CE0.10: Caso especial de la ecuación cúbica. Tartaglia - 1545). | SP0.10: Resolver un caso particular de la ecuación cúbica. | SIP.10: Método de Tartaglia para resolver la ecuación cúbica. |
Período cero (edad antigua: del 3500 a.C. al siglo V d.C. - Edad media: siglo V al siglo XV), se relaciona con la problemática de resolver ecuaciones algebraicas de grado 1, 2 y 3. Como no existía una representación algebraica, se establece un significado pre-algebraico de Grupo, que corresponde a las raíces de la ecuación algebraica de grado uno y dos y las permutaciones de estas, ver Tabla 1.
El período uno: se considera también un significado algebraico de Grupo, que en la edad media corresponde a los conjuntos de permutaciones de las raíces de las ecuaciones, las raíces 𝑛 de la unidad y funciones definidas en estos conjuntos. En la edad moderna (S XV - S XVIII), el significado de grupo corresponde a: conjuntos de permutaciones de las raíces de las ecuaciones algebraicas de grado 2, 3 y 4; conjunto de los enteros módulo
Tabla 2 Sistemas de prácticas para resolver los problemas SP1.
| Prácticas Matemáticas (CE) | Situación problema (SP) | Significado parcial (SIP) |
|---|---|---|
| CE1. Relación entre los coeficientes y las raíces de las ecuaciones algebraicas de grado dos, tres y cuatro y el problema del simbolismo algebraico. | SP1. Establecer relaciones entre los coeficientes y las raíces de las ecuaciones algebraicas y el simbolismo algebraico. | SIP1. Polinomios simétricos. |
| CE1.1: Ecuaciones algebraicas en la escuela italiana. | SP1.1: Resolver ecuaciones algebraicas y el simbolismo algebraico. | SIP1.1: Relación entre los coeficientes de las ecuaciones algebraicas y sus raíces. |
| CE1.2: Ecuación bicuadrática. Ferrari (1540) | SP1.2: Resolver la ecuación bicuadrática de manera general. | SIP1.2: Método de Ferrari para resolver la ecuación bicuadrática, conjuntos Sn. |
| CE1.3: Ecuaciones algebraicas a través de problemas geométricos. Descartes (1637) | SP1.3: El problema de Pappus. | SIP1.3: Lugar geométrico de puntos bajo condiciones dadas. Método de Descartes. |
| CE1.4: El simbolismo de Vieta y Harriot (1631). | SP1.4: Representar en forma algebraica una ecuación. | SIP1.4: Simbolismo algebraico. |
| CE1.5: Teorema fundamental del álgebra de Girard (1629). | SP1.5: Determinar cuántas raíces tiene una ecuación algebraica de grado n. | SIP1.5: Raíces de un polinomio de grado n. |
| CE1.6: Los polinomios simétricos de Newton. | SP1.6: Hallar las relaciones entre los coeficientes y las raíces de las ecuaciones algebraicas. | SIP1.6: Polinomios simétricos, conjuntos Sn. |
| CE1.7: Ecuación algebraica de cuarto grado. | SP1.7: Resolver la ecuación algebraica de grado 4. | SIP1.7: Método de Euler para solucionar la ecuación de grado cuarto, conjuntos Sn y Z n |
| CE1.8: Aritmética Modular | SP1.8: Demostrar el pequeño teorema (Fermat). | SIP1.8: Pequeño teorema de Fermat, conjuntos Z n . |
| CE1.9: Las resolventes de la ecuación cúbica | SP1.9: Determinar las resolventes de Lagrange para la ecuación cúbica | SIP1.9: Resolventes de Lagrange de la ecuación cúbica, conjuntos S n conjunto de raíces de la unidad. |
En el periodo dos, edad contemporánea (1789-actualidad), los significados de grupo siguen siendo algebraicos, como el conjunto de permutaciones, caso particular
Tabla 3 Sistemas de prácticas para resolver los problemas SP2.
| Prácticas Matemáticas (CE) | Situación problema (SP) | Significado parcial (SIP) |
|---|---|---|
| CE2. Búsqueda de métodos generales para la solución de la ecuación algebraica de grado 𝒏 y la imposibilidad de solución de la ecuación de grado n > 4. | SP2. Resolver ecuaciones algebraicas generales de grado n>4, por el método de radicales. | SIP2. Ecuación general de grado cinco, método de radicales. |
| CE2.1: Tratamiento de la ecuación de grado quinto por Ruffini. (1805). | SP2.1: Imposibilidad de resolver la ecuación general de grado cinco por radicales. | SIP2.1: Método de Ruffini para resolver la ecuación de grado quinto. |
| CE2.2: Teorema de Ruffini propuesto por Cauchy (1815). | SP2.2: Generalizar el Teorema de Ruffini. | SIP2.2: Teorema de Cauchy. |
| CE2.3: Tratamiento a la ecuación de grado quinto por Abel (1824). | SP2.3: Imposibilidad de resolver la ecuación algebraica general de grado quinto por radicales. | SIP2.3: La ecuación general de grado quinto es irresoluble por el método de radicales. |
En el periodo tres, ubicado también en la edad contemporánea, los significados son conjuntos de permutaciones, conjuntos alternantes An de las permutaciones pares, grupo de Galois del polinomio, grupos simples y grupos solubles, ver Tabla 4.
Tabla 4 Sistemas de prácticas para resolver los problemas SP3.
| Prácticas Matemáticas (CE) | Situación problema (SP) | Significado parcial (SIP) |
|---|---|---|
| CE3. Ecuaciones algebraicas solubles por el método de radicales. | SP3. Clasificar las ecuaciones algebraicas. | SIP3. Ecuaciones solubles por radicales. |
| CE3.1: Grupos abelianos, ecuación ciclotómica. Gauss, (1798). | SP3.1: Resolver problemas con aritmética modular de Gauss. | SIP3.1: Conjuntos Z n , conjunto de las raíces de la ecuación x n = 1. |
| CE3.2: Las ecuaciones ciclotómicas de Gauss. Gauss, (1801) | SP3.2: Resolver ecuaciones ciclotómicas. | SIP3.2: Método para determinar las raíces de una ecuación ciclotómica, conjuntos de las raíces de la ecuación x n = 1. |
| CE3.3: Ecuaciones solubles. Galois, (1831). | SP3.3: Determinar si una ecuación es soluble por radicales. | SIP3.3: Grupo de Galois asociado a la ecuación polinómica, grupo de Galois del polinomio. |
El periodo cuatro se ubica en la edad contemporánea: el significado de Grupo se considera como ‘abstracto’ y corresponde a la definición de Cayley: “Un grupo es un conjunto, con una operación binaria, tal que la operación cumple los axiomas de clausura, asociatividad, existencia de un elemento neutro, y existencia de un elemento inverso para cada elemento del conjunto, (Castellet & Llerena, 2000, p.63). Este significado es de referencia, y se incorpora en los currículos en el contexto Colombiano. Otros significados, son: Grupo de los cuaterniones con la suma, grupos de matrices invertibles con la multiplicación, grupos de permutaciones con la compuesta; grupos de transformaciones, fundamentales para clasificar las geometrías por Félix Klein; grupos continuos de transformaciones o grupos de Lie, aplicados a la geometría y a las ecuaciones diferenciales parciales, desarrollados por Sophus Lie; Grupo cristalográfico, Grupo puntual y grupos abelianos finitos. A partir de este período, emergen aplicaciones en contextos matemáticos y extra-matemáticos, ver Tabla 5.
Tabla 5 Sistemas de prácticas para resolver los problemas SP4.
| Prácticas Matemáticas (CE) | Situación problema (SP) | Significado parcial (SIP) |
|---|---|---|
| CE4. Clasificación de grupos en el siglo XIX | SP4. Definir y clasificar el objeto algebraico Grupo | SIP4. Definición de grupo algebraico considerando las propiedades operación interna para los elementos. |
| CE4.1: Definición de grupo dada por Cayley. | SP4.1: ¿Qué es un grupo? | SIP4.1: Primera definición abstracta de Grupo, grupo Z n Ggrupo de Matrices, Grupo S n Grupo de los Cuaterniones. |
| CE4.2: Grupos continuos de transformaciones. | SP4.2: Establecer propiedades generales de los grupos continuos finitos de transformaciones. Hallar el grupo de Lie. | SIP4.2: Grupos de Lie, grupos simples, grupos solubles |
| CE4.3: Clasificación de las Geometrías según Klein. | SP4.3: Clasificar las Geometrías. | SIP4.3: Grupo principal de las Transformaciones del espacio. |
| CE4.4: Los grupos finitos simples. | SP4.4: Clasificar los grupos finitos simples | SIP4.4: Grupo finito simple. |
| CE4.5: Grupos cristalográficos. | SP4.5: Clasificar los grupos cristalográficos. ¿Cuáles son los generadores de un grupo cristalográfico? | SIP4.5: Grupo cristalográfico. |
| CE4.6: Los grupos puntuales. | SP4.6: Clasificar los grupos puntuales. | SIP4.6: Grupo puntual de la molécula |
| CE4.7: Grupos en Física. | SP4.7: ¿Qué grupos se utilizan en Física? | SIP4.7: Grupo de desplazamientos, Grupo de rotaciones, Grupos de simetría de las partículas, grupos cristalográficos, grupos de permutaciones, Grupo de Lorentz. |
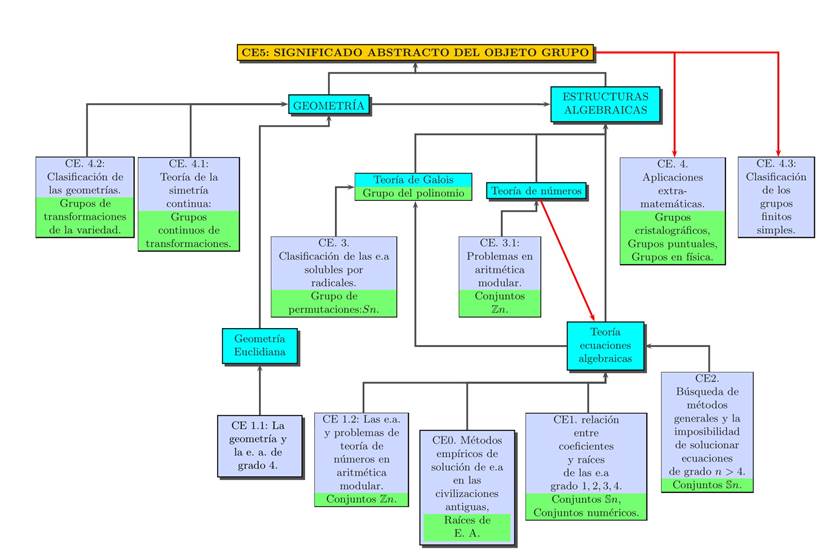
En la Figura 1, se presentan las relaciones entre las configuraciones epistémicas en la emergencia del objeto Grupo, que dieron origen a áreas de la matemática, como: la Geometría, Teoría de números, Teoría de Ecuaciones Algebraicas y Teoría de la Simetría Continua.
Significados del objeto Grupo pretendidos en los libros de texto de álgebra abstracta
En esta sección se establece el significado institucional o de referencia de los libros: Gallian (2006), Herstein (1986), Lezama (2013) y Caicedo (2004), que se utilizan en cursos de Teoría de Grupos en programas de formación profesional en matemática, como resultado del análisis semiótico fundamentado en el EOS (Sepúlveda, 2015), y de las síntesis de la tablas 1 a 5. Este análisis es importante porque el texto es un recurso potente para el profesor, al momento de organizar el proceso de enseñanza y aprendizaje (Remillard, 2000). En este sentido, se da respuesta a las preguntas: ¿Cuáles son los objetos matemáticos vinculados con el objeto Grupo?, ¿Cómo se introduce su estudio?, ¿Se tiene en cuenta su desarrollo histórico, desde los distintos significados hasta llegar a la construcción del objeto?, ¿Cuál es la representatividad de los significados parciales respecto al significado Global, de la estructura Grupo?
Al respecto, en el libro de Gallian (2006), el capítulo “preliminares” presenta una introducción de Grupo como un conjunto particular sobre el que se define una operación que cumple las propiedades algebraicas (asociatividad, existencia de módulo, existencia de inverso), que se identifican con el objeto primario proposiciones, para inferir el significado de Grupo en aritmética modular Z n (CE1.8).
En el capítulo uno parte 3, presenta los grupos diedrales a partir del conjunto “simetrías del cuadrado” en el contexto de los movimientos de un polígono regular; e incluye el significado de grupo de permutaciones (CE1.7 y CE1.9). Los objetos matemáticos primarios identificados, son: las propiedades de la operación composición definida sobre el conjunto de las funciones de simetrías del cuadrado 𝐷 4 ; los argumentos sobre D4, por ejemplo en este grupo no se cumple la propiedad conmutativa (CE1.9, CE4.1); los conceptos de rotación, traslación y reflexión en el grupo diedral de orden 2n (CE1.9) y las propiedades de estos grupos de ser cíclicos (CE4.1); las situaciones extra-matemáticas de las simetrías de una molécula piramidal (CE4.6) relacionadas con D4 y el grupo determinado por la estructura interna de un cristal (CE4.5). Finalmente, presenta situaciones- problemas intra-matemáticas y extra-matemáticas (CE1.9 y CE4.1). En el capítulo dos, Grupos, presenta el significado abstracto de este objeto (CE4.1).
En el capítulo tres, Grupos finitos y Subgrupos, propone dos pruebas para determinar cuándo un subconjunto de un grupo es subgrupo (CE4.1), y presenta el objeto como un conjunto de permutaciones a partir de “las simetrías de los polígonos regulares”, que corresponde históricamente a uno de los primeros significados (CE1.9 y CE4.1).
El capítulo cuatro explica las propiedades de los grupos cíclicos (CE4.1); en el capítulo cinco define grupos de permutaciones y sus notaciones, presenta problemas de aplicación en contextos como las simetrías de los polígonos regulares D n (CE1.2, CE1.6, CE1.7, CE4.1) y establece relaciones de homomorfismos e isomorfismos entre casos particulares de Grupos (CD1-Configuración didáctica emergente).
Por su parte, en libro de Herstein (1986), en el capítulo uno propone y resuelve situaciones-problemas orientadas a verificar las propiedades de una operación definida en un conjunto dado (CE4.1), organizadas en las siguientes lecciones: 1) Teoría de Conjuntos, define operaciones entre conjuntos y propiedades de estas, define los conceptos de función inyectiva, sobreyectiva y biyectiva, propone situaciones-problemáticas contextualizadas (fáciles, de nivel medio y duros) relacionadas con las propiedades de las funciones; 2) Permutaciones, define este conjunto como las funciones biyectivas definidas de un conjunto finito S en el mismo y lo nota como A(S) (CE1.9), el cual con la operación compuesta cumple los axiomas de grupo, argumenta que A(S) es el “Grupo de simetrías de grado n” por el cardinal de S y lo representa como S n ; 3) Los enteros, expone las propiedades del principio del buen orden, el algoritmo de Euclides, define los conceptos y propiedades de divisibilidad, máximo común divisor, primo relativo, número primo (CE1.8); 4) Inducción matemática, presenta la proposición de este principio y propone situaciones problemas; y 5) Números complejos, presenta los grupos formados por este conjunto con la operaciones suma y con la operación producto (CE1.7, CE4.1).
El capítulo dos, Grupos, inicia con la argumentación que A(S) es grupo, lo que permite inferir que el significado atribuido a grupo corresponde a un conjunto de permutaciones, además presenta su significado abstracto (CE4.1). Los objetos matemáticos identificados son: 1) conceptos y propiedades de A(S) (CE4.1); 2) Situaciones-problemas, relacionadas con verificar la estructura de grupo en los conjuntos numéricos de los enteros con la adición, los racionales con la adición, los racionales sin el cero con la multiplicación ordinaria, los reales positivos con el producto ordinario (CE4.1), el subconjunto de los complejos de las raíces de la unidad con la multiplicación (CE3.1); el conjunto de funciones reales T(a,b) con la composición (CE4.2, CE4.1); verificar que algunos conjuntos numéricos con ciertas operaciones no alcanzan la estructura de grupo, como los enteros con el producto, los reales con la operación a * b = a3b y los enteros positivos con el producto usual (CE1.8); y otras situaciones propias de la matemática (CE1.7, CE1.8 y CE4.1); 3) Argumentos de tipo histórico, como “el tiempo que le tomó al hombre en reconocer que las cuatro propiedades algebraicas son fundamentales en la matemática” y otros relacionados sobre conjuntos numéricos y sus operaciones usuales; 4) Propiedades deducidas de los axiomas de grupo.
En el capítulo tres, define los conceptos de grupos finitos y subgrupos, presenta pruebas para determinar cuándo un subconjunto de un Grupo es el mismo Grupo (CE4.1 y CE4.2).
En el libro de Lezama (2013), en el Capítulo uno, Grupos y subgrupos presenta los siguientes conceptos o propiedades, siguiendo este orden: 1) Operación binaria interna en un conjunto G, incluye las situaciones-problema para contextualizar este concepto con las funciones de suma en los números naturales (CE1.8, CE4.1),
De lo anterior, se infiere que Lezama (2013), introduce el objeto Grupo a partir de las propiedades de la operación definida en el conjunto desde la estructura de semigrupo, monoide y finalmente el significado abstracto (CE4.1).
En el libro de Caicedo (2004), se evidencia lo siguiente: En el capítulo uno, Grupos, presenta el concepto de “ley de composición interna” en un conjunto E (CE4.1); presenta situaciones-problemas que dado un conjunto numérico y una operación definida sobre este (naturales con la suma, naturales con el producto, enteros con la suma, enteros con el producto, reales positivos con el producto), verificar si la operación es binaria y cumple los axiomas de grupo (CE1.8, CE4.1); presenta el conjunto de funciones biyectivas definidas de un conjunto S no vacío en sí mismo, notado B(S) y define sobre estas funciones la operación composición argumentando las propiedades de clausura, asociativa, elemento identidad y existencia de inversos sin enunciarlas formalmente (CE1.2, CE1.6, CE1.7, CE1.9 y CE4.1).
Respecto a los objetos primarios, se identifican los siguientes: en la lección uno, las proposiciones que cumplen las operaciones definidas sobre conjuntos numéricos mencionados anteriormente, (CE1.8 y CE4.1); en la lección dos, los conceptos o definiciones de Grupo y Grupo Abeliano (CE4.1), las siguientes situaciones-problema de verificar si el conjunto con la operación definida sobre este es una estructura de grupo: funciones biyectivas con la composición (CE1.2, CE1.6, CE1.7, CE1.9 y CE4.1), partes de un conjunto con la diferencia simétrica (CD1), números reales sin el cero con el producto usual, números complejos sin el cero con el producto usual de complejos, números enteros con la adición usual, el intervalo abierto I = (-1,1) con el producto usual (CE1.8), las raíces cuartas de la unidad G = {-1,1,i,-i} con el producto usual de números complejos (CE3.1 y CE3.2), rectas con pendiente no nula (L={(a,b) ∈ R2, α es la pendiente distinta de cero y b es el corte con el eje y}) con la compuesta de funciones (CE4.2, CE4.3), el conjunto L con el producto entre parejas; en la lección tres, presenta propiedades de la unicidad del elemento neutro y del inverso, verificar las propiedades cancelativas a izquierda, a derecha y en general los axiomas de grupo (CE4.1). Al final del capítulo presenta 13 situaciones-problema para contextualizar los objetos matemáticos dados en cada una de las lecciones.
Del análisis del texto de Caicedo (2004), se infiere que introduce el objeto Grupo desde los significados abstractos (CE4.1) y como conjunto de permutaciones (CE1.2, CE1.6, CE1.7, CE1.9).
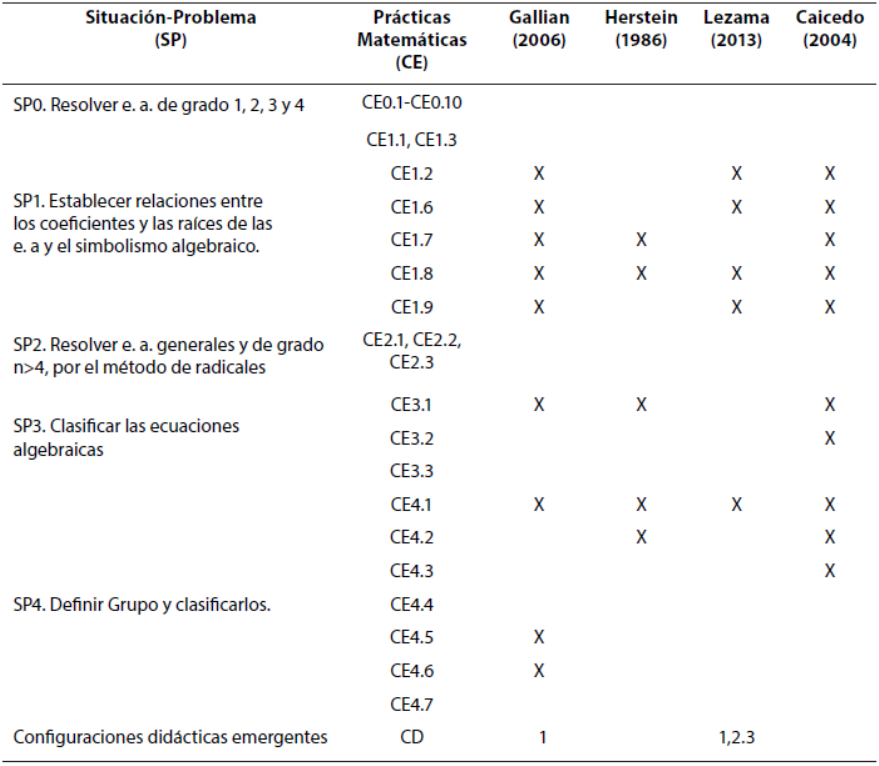
En la Tabla 6, se resume la relación entre las situaciones-problemas y las prácticas matemáticas llevadas a cabo para su solución, que fueron analizados en los cuatro textos. De esta se concluye que los libros no abordan la configuración epistémica CE0 y por tanto no se estudian los grupos de Galois; además, el orden de los libros con la cantidad de significados parciales de la estructura grupo, corresponden a: Herstein (1986), Gallian (2006), Caicedo (2004) y Lezama (2013).
3.2 Construcción de significados del objeto Grupo
Se proponen a continuación dos situaciones-problemas para resolver la ecuación algebraica de grado 3, relacionadas con la configuración epistémica (CE1.9), que surgen del trabajo de Lagrange (1736-1813) y los aportes de: Omar Khayyam (1050-1133) quien presenta soluciones geométricas utilizando intersecciones de cónicas y muestra la imposibilidad de resolverlas por métodos aritméticos; Scipione Del Ferro (1465-1536) y Gerolamo Cardano (1501-1576), resuelven ecuaciones del tipo (1) y Gauss expone propiedades de los números complejos (Sepúlveda, 2017; 2018).
Con estas situaciones, se pretenden dar respuesta a las preguntas: ¿Cómo promover la construcción del significado parcial del Grupo de los enteros módulo tres y el Grupo de simetría S3 a partir del análisis del método de solución de Lagrange para la ecuación de tercer grado, en estudiantes de Teoría de Grupos?, ¿Cómo se adaptan las configuraciones epistémicas del objeto Grupo, al diseño de procesos de instrucción para evidenciar la riqueza matemática del objeto de estudio?, ¿Cómo utilizar los recursos tecnológicos (Software especializado) en el diseño de estos procesos de instrucción? y ¿Cómo generar nuevas configuraciones epistémico-didácticas para la enseñanza de nociones de Teoría de Grupos?
Situación problema 1: Resolver la ecuación algebraica de tercer grado, ecuación (2), por el método de la resolvente de Lagrange. Para esto, Lagrange propone los siguientes pasos.
1. Anular el coeficiente 𝑎 en (2) al sustituir la expresión (3) en (2) y determinar h.
2. Verificar que ℎ, corresponde a la expresión (4).
3. Verificar que la ecuación resultante en la variable 𝑦 es la ecuación (5).
4. Mostrar que las raíces cúbicas de la unidad, 𝜔 3 =1, son las relacionadas en (6).
5. Comprobar que las raíces en (6) con la multiplicación, satisfacen lo siguiente,
6. Si, 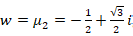 , verificar las igualdades presentadas en (7)
, verificar las igualdades presentadas en (7)
7. Mostar que 𝑤 satisface las ecuaciones presentadas en (8),
8. Sea { 𝑥 1 , 𝑥 2 , 𝑥 3 } las raíces de la ecuación (5) y
9. Mostrar las igualdades de (15), a partir de las ecuaciones (9) a (14):
10. Construir la ecuación algebraica de grado seis, dada en (16),
11. Verificar que al remplazar (9) a (14) en (16) se obtiene el polinomio (17) en la variable
12. Verificar que al reemplazar las relaciones de (15), (7), (8) en (17) se obtiene el polinomio (18).
13. Verificar que la ecuación (5), con raíces 𝑥₁,𝑥₂ y 𝑥 3 , es igual a la ecuación (19)
14. Comparar las ecuaciones (5) y (19), para determinar las identidades de Girard, relaciones en (20):
15. Verificar que las relaciones (9) y (10) satisfacen (21), que corresponde al coeficiente de 𝑦³ en (18).
16. Hacer la sustitución (22) y verificar que se cumple la relación (23) y (24)
17. Reemplazar las expresiones (22), (23) y (24) en la ecuación (21), para obtener la ecuación (25),
18. Comprobar la relación (26)
19. Aplicar las identidades de Girard y la ecuación (26), para establecer la relación (27),
20. Verificar las relaciones (28) a (32) para establecer la expresión (33), que corresponde al término independiente del polinomio de la ecuación (18).
21. Reemplazar 𝑧= 𝑦 3 en la ecuación (18) para obtener la ecuación (34):
22. Reemplazar las expresiones (27) y (33) en (34) para obtener el polinomio relacionado en (35):
23. Hacer las sustituciones de (36) en las ecuaciones (34) y (35), y obtener la ecuación (37)
24. Resolver la ecuación (35) y verificar las expresiones (38) y (39)
25. Para hallar la solución 𝑥₁, de (9) y (10) verificar que se tiene la relación (40):
26. Comprobar que el valor de 𝑥₁, esta dado por la expresión (41):
27. Verificar que la primera solución de la ecuación (5), está dada por (42):
28. De manera similar, verifique que la segunda y tercera solución de la ecuación (5), están dadas por la expresión (43) y (44):
29. Con las soluciones x1, x2 y x3 halle las soluciones de la ecuación (2).
Situación problema 2: Identificar los grupos (Z3, +) y (S3, o) en el método desarrollado por Lagrange para la solución de la ecuación (2). Para esto se proponen las siguientes actividades:
1. Considerar el conjunto de las raíces cúbicas de la unidad {1,w,w2}, con la multiplicación
a. Demuestre que ({1,w,w2};) es un Grupo Abeliano.
b. Pruebe el isomorfismo entre el grupo de las raíces cúbicas de la unidad y el grupo de los enteros módulo 3, ({1,w,w2}, ∙ )
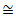 (Z3 = {0,1,2}, +).
(Z3 = {0,1,2}, +).
c. Argumente porqué Lagrange no llegó a identificar axiomas de grupo en ({1,w,w2};) y por tanto no puedo concebir la estructura de grupo de (Z3 = {0,1,2}, +).
2. Representación de las relaciones de Lagrange r1, r2, r3, r4, r5, r6, identificadas en la situación problema uno, ecuaciones de (9) a (14).
a. En la relación r1 = µ1 x1 + µ3 x2 + µ3 x3, los sumandos establecen la función ƒ1, entre el conjunto de raíces de la unidad {µ1, µ2, µ3} con las raíces de (5). Represente ƒ1 = {(µ1, x1), (µ2, x2), (µ3, x3)}.
b. Representar ƒ1 como una permutación.
𝑐. Repetir los ítems a. y b. para las relaciones de Lagrange r2, r3, r4, r5, r6.
d. Si ∘ es la composición de funciones, pruebe que ({ƒ1, ƒ2, ƒ3, ƒ4, ƒ5, ƒ6},°) es un grupo no conmutativo,
e. Argumente porqué Lagrange no identificó los axiomas de grupo en el conjunto S3 de permutaciones con 3 elementos con la operación compuesta de funciones.
4. Conclusiones
Es necesario presentar una muestra representativa e interconectada de significados del objeto matemático grupo a los alumnos, respecto de un significado de referencia, lo que les permite resolver tipos de problemas diferentes. Por lo cual, si se quiere enseñar una muestra representativa de significados parciales, es necesario presentar una muestra variada de problemas (Font, Breda & Seckel, 2017). Y a su vez, si se quiere conseguir que el alumno sea competente en la resolución de una variedad de problemas donde el objeto matemático en cuestión tiene un rol determinante, se requiere que los alumnos dispongan de una red de significados parciales bien conectados entre sí.
Al respecto, el análisis epistemológico y fenomenológico sugiere lo siguiente: 1) Para la enseñanza y aprendizaje del objeto grupo, se deben seguir algunos de los aspectos de su evolución, desde la solución de ecuaciones algebraicas hasta llegar al grupo de Galois del polinomio, que promovió el desarrollo de una teoría completa para dar solución al problema de la irresolubilidad de las ecuaciones algebraicas de grado quinto y superiores por radicales; 2) Los cinco bloques de problemas y las 32 CE emergentes, orientan la formulación de otras situaciones y el diseño e implementación de estrategias de enseñanza, para que los estudiantes construyan los significados parciales y el significado holístico de grupo.
Del análisis de textos, se concluye que los significados de referencia del objeto son: 1) Grupos de conjuntos numéricos con las operaciones usuales, Grupos en aritmética modular Z n , los grupos S n de permutaciones de orden n (CE1.6,CE1.7,CE1.8, CE4.1), los grupos D n de simetrías de polígonos regulares, , grupos de transformaciones con la composición de funciones; 2) Pretenden el significado abstracto de grupo a partir de verificar los axiomas de grupo en conceptos como ley de composición interna, semigrupo, monoide, grupo y grupo conmutativo (CE4.1).
Las situaciones problemas diseñadas, promueven la construcción de significados parciales de grupo como el conjunto de raíces de la unidad, grupo de permutaciones y grupo Z3 isomorfo al grupo de raíces de la unidad: fundamentados pero no emergentes, del trabajo de Lagrange, evidenciando la riqueza matemática del objeto, hasta llegar al significado holístico o abstracto y verificar la relación de isomorfismos entre grupos.