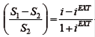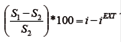INTRODUCCIÓN
Tradicionalmente, las dinámicas y relaciones de los tipos de cambio, las tasas de interés y los precios se analizan en los estudios financieros y, en menor medida, en los estudios económicos. Particularmente, en las finanzas internacionales se suele justificar la conveniencia de analizar dichas relaciones en términos de la necesidad que tienen las firmas multinacionales, los inversionistas y los agentes en los mercados para: a) financiarse e invertir sus recursos de la mejor manera posible, b) realizar acciones de arbitraje en los mercados y c) hacer pronósticos de las variables con base en las dinámicas y relaciones observadas. Por estas razones, desde hace varios años se han propuesto varias teorías para explicar dichas relaciones.
Las hipótesis de Fisher son dos teorías complementarias que explican las relaciones entre los tipos de cambios, las tasas de interés y los precios en el largo plazo (Eiteman, Stonehill y Moffet, 2013). La hipótesis de Fisher en su versión doméstica sostiene que hay una relación directa entre las tasas de interés nominales y la inflación esperada. Esta teoría es relevante porque permite analizar los efectos de las políticas monetaria y, eventualmente, explicar los ciclos económicos (Fisher, 1930; Argandoña, 2013). Por su parte, la hipótesis de Fisher en su versión internacional sostiene que hay relaciones inversas entre las tasas de interés y los tipos de cambio. Esta teoría es relevante porque se vincula a las hipótesis de integración de los mercados financieros (Hatemi-J, 2009).
Las hipótesis de Fisher tienen implicaciones económicas y financieras importantes. A nivel macroeconómico, estas implicaciones se refieren a la integración de los mercados monetarios, cambiarios y de bienes y servicios; a las dinámicas de los tipos de cambio, las tasas de interés y los precios de largo plazo, y a los efectos de la política monetaria en el corto y largo plazos. A nivel microeconómico, estas implicaciones se refieren a las decisiones de financiamiento, inversión, consumo y ahorro de los agentes, y a la posibilidad de obtener ganancias extraordinarias mediante acciones de arbitraje. En este contexto, el estudio de las hipótesis de Fisher puede justificarse con base en razones de interés público y privado.
Paradójicamente, no hay muchos estudios contemporáneos que hayan abordado las hipótesis de Fisher en Latinoamérica. La mayoría de los estudios existentes son de la última década del siglo pasado y de los primeros años del siglo XXI. Esta escasez de estudios puede explicarse por diversas razones: en primer lugar, hasta hace pocos años, la disponibilidad de usar series comparables referidas a los mercados latinoamericanos había sido muy limitada; en segundo lugar, muchos países de la región han tenido niveles muy altos de intervención gubernamental y regímenes cambiarios predominantemente fijos; finalmente, la mencionada escasez también puede explicarse por problemas metodológicos vinculados a la existencia de choques internos y externos, crisis y procesos de reforma y ajuste en la región.
En este estudio se evalúan las hipótesis de Fisher y de integración de los mercados latinoamericanos. Estas evaluaciones se sustentan en la metodología de cointegración de Johansen (1991). Así, se estudian: a) el comportamiento de las series de tipos de cambio, tasas de interés y precios, b) la existencia de cambios estructurales en estas series, c) las relaciones de largo plazo de las series y d) la validez de las hipótesis analizadas. El estudio utiliza estadísticas descriptivas, correlaciones pairwise y pruebas de raíz unitaria, de cambio estructural endógeno y de cointegración. La base de datos analizada incluye series mensuales de Brasil, Chile, Colombia, Costa Rica, México y Perú para el periodo comprendido entre enero de 1997 y diciembre de 2014.
El estudio complementa la literatura referida a las dinámicas de los tipos de cambio, las tasas de interés y los precios en Latinoamérica; sus contribuciones son econométricas y analíticas. El estudio tiene similitudes metodológicas con los trabajos de Phylaktis y Blake (1993), Berument y Jelassi (2002), Juselius y MacDonald (2004) y Hatemi-J (2009). Su contribución econométrica consiste en estudiar la existencia de cambios estructurales en las variables de manera endógena; la contribución analítica es la evaluación de las hipótesis de Fisher y de integración de los mercados para los países mencionados, entre 1997 y 2014. Los estudios existentes suelen estudiar su validez, aunque no de manera conjunta, para Brasil, Chile, Costa Rica y México.
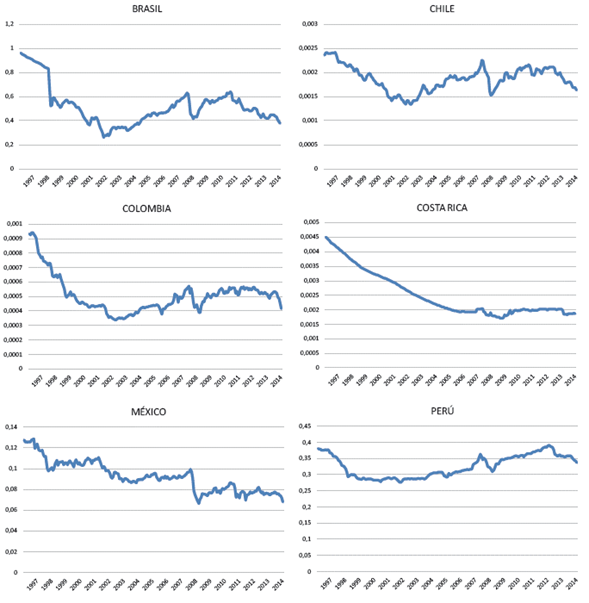
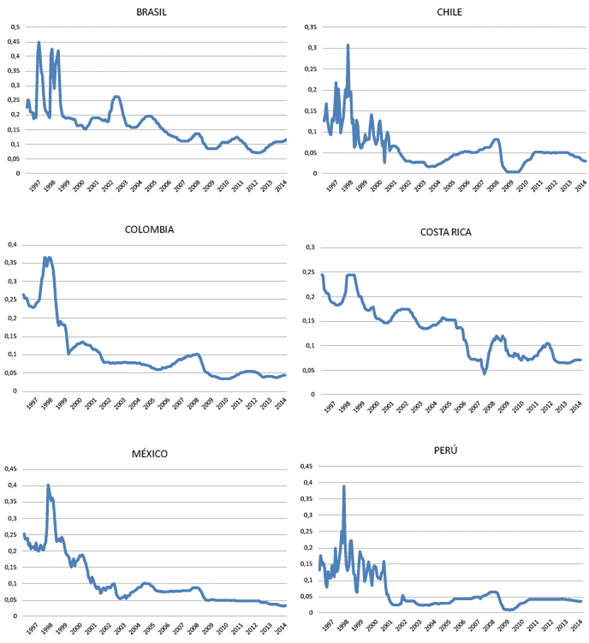
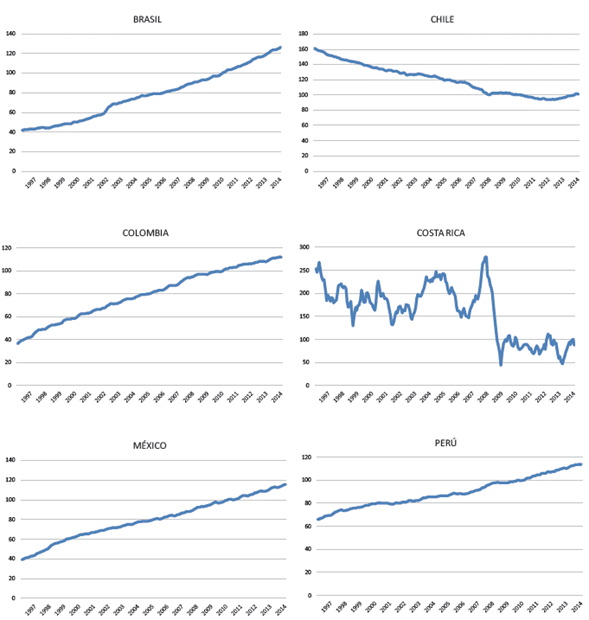
El estudio está organizado en seis secciones. La sección siguiente incluye la revisión de la literatura, se explican las hipótesis de Fisher y se discute la metodología de los estudios que han evaluado su validez. Luego se describe la metodología del análisis econométrico. En la sección posterior se describe la base de datos y se muestran los análisis estadísticos, de raíces unitarias y de cambio estructural. Después se procede a los análisis de cointegración con base en la metodología de Johansen (1991), para evaluar la validez de las hipótesis de Fisher y de la integración de los mercados latinoamericanos. La sección última sintetiza los resultados y discute sus implicaciones. El (apéndice) muestra, de manera gráfica, las series usadas en la investigación.
REVISIÓN DE LA LITERATURA
En esta sección se revisa la literatura referida a las teorías y a la validación de las hipótesis de Fisher y de la integración de los mercados. La sección se divide en dos apartados: en el primero se explican las hipótesis de Fisher y su vinculación con la hipótesis de integración de los mercados; en el segundo se revisan los estudios que han evaluado las hipótesis de Fisher en sus versiones doméstica e internacional, y se discute su metodología. La revisión de la literatura enfatiza las implicaciones vinculadas a las hipótesis de Fisher y los estudios hechos para los países latinoamericanos. Así, se justifica la pertinencia y los alcances del estudio aquí planteado, al tiempo que permite contextualizarlo en términos de la literatura existente.
Las hipótesis de Fisher: teorías e implicaciones
Las hipótesis de Fisher son dos teorías que contribuyen a explicar las relaciones entre los tipos de cambios, las tasas de interés y los precios en el largo plazo cuando no hay intervención gubernamental y tipos de cambio flexibles. Particularmente, la hipótesis de Fisher en su versión doméstica postula que "las tasas de interés nominales en cada país son iguales a la tasa de rendimiento real, más la compensación requerida para la inflación esperada" (Eiteman, Stonehill y Moffett, 2013, p. 93)1. Por su parte, la hipótesis de Fisher en su versión internacional sostiene que "el tipo de cambio al contado debería variar en una cantidad igual, pero en la dirección opuesta a la diferencia entre las tasas de interés de dos países" (Eiteman, Stonehill y Moffett, 2013, p. 194)2.
Las hipótesis de Fisher forman parte de las condiciones internacionales de paridad (CIP), las cuales integran el núcleo de las teorías financieras que se consideran como exclusivas de las finanzas internacionales (Eiteman, Stonehill y Moffett, 2013, p. 185). Las teorías que las integran son las siguientes: a) la hipótesis de Fisher en su versión internacional, b) la hipótesis de Fisher en su versión doméstica, c) la teoría de la paridad de poder de compra, d) la teoría de la paridad de las tasas de interés y e) la teoría de la eficiencia de mercados. Estas cinco teorías establecen un marco de correlaciones que explican los comportamientos en el largo plazo de los tipos de cambios, las tasas de interés y los precios en equilibrio (gráfica 1)3.
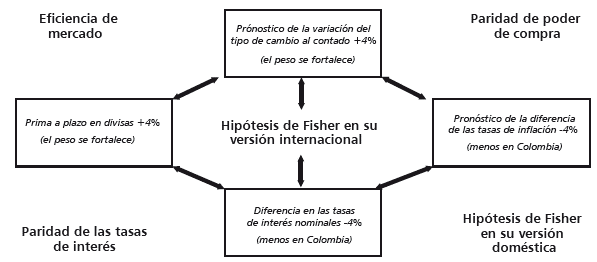
Fuente: elaboración de los autores con base en Eiteman, Stonehill y Moffet (2013, p. 213).
Gráfica 1 Condiciones internacionales de paridad en el equilibrio
Las hipótesis de Fisher tienen implicaciones económicas y financieras importantes. Su validez implica que cuando la economía experimentara choques, las variables se ajustarían para recuperar sus niveles de largo plazo. En este contexto, las políticas monetarias solo tendrían efectos de corto plazo sobre los tipos de cambio (Baxter, 1994). Alternativamente, la validez de las hipótesis implicaría que los bancos centrales podrían usar las tasas de interés como indicadores para fijar sus objetivos de inflación de largo plazo (Granville y Mallick, 2004; Badillo, Reverte y Rubio, 2010). Las hipótesis también implican que no sería posible realizar acciones de arbitraje mediante activos financieros (Solnik, 1978) y, más aun, que los agentes no serían aversos al riesgo y que los mercados serían eficientes (Gaab, Granziol y Horner, 1986).
La hipótesis de Fisher en su versión internacional usualmente se vincula a las hipótesis de integración de los mercados financieros (Hatemi-J, 2009). De hecho, hay quienes argumentan que una perfecta integración de los mercados financieros ocurre cuando se cumplen las siguientes condiciones vinculadas a la hipótesis de Fisher (Oxelheim, 1990): a) si se cumple el supuesto de neutralidad al riesgo y b) si las diferencias en las tasas de interés de los países tienden a igualarse con los tipos de cambio esperados. Por esta razón, en la investigación aquí presentada, la evaluación de la hipótesis de la integración de los mercados financieros se plantea en términos de una extensión de la validez de la hipótesis de Fisher en su versión internacional.
Los estudios empíricos relativos a las hipótesis de Fisher: metodologías y controversias
Los estudios contemporáneos relativos a la validación de las hipótesis de Fisher usan la metodología de Johansen (1991) con fines de evaluación empírica. Esta metodología se usa para investigar si hay movimientos conjuntos y equilibrios de largo plazo entre grupos de variables. Particularmente, en algunos de dichos estudios la validación de las hipótesis de Fisher ocurre cuando hay relaciones empíricas de largo plazo similares a aquellas postuladas de manera teórica. Así, la hipótesis en su versión doméstica requiere que existan relaciones directas entre las tasas de interés y los precios (i. e., la inflación esperada), a nivel nacional. La hipótesis en su versión internacional requiere que existan relaciones inversas entre las tasas de interés y los tipos de cambio.
En términos estadísticos, la metodología de Johansen requiere que los tipos de cambio, las tasas de interés y los precios cumplan con ciertos requisitos. El principal de ellos es que las variables deben ser integradas de orden uno, I(1). Esto significa que las series de datos deben tener una raíz unitaria, lo cual es importante señalar porque las relaciones estimadas con series I(1) dan lugar al fenómeno de "regresión espuria" (Brooks, 2008)4. Por tanto, una evaluación de las hipótesis de Fisher sustentada solamente en correlaciones o regresiones de series I(1) pudiera no ser idónea. Por esta razón, hay consensos metodológicos en torno a que los estudios relativos a la validación de las hipótesis de Fisher deben incluir pruebas de raíces unitarias y de cointegración5.
Paradójicamente, en la literatura empírica existen controversias sobre si se cumplen o no las hipótesis de Fisher pese a la existencia de los consensos metodológicos (Cooray, 2003). Así, hay quienes creen que la hipótesis en su versión doméstica solo se cumple bajo condiciones limitadas6. La literatura provee resultados no concluyentes, entre otras razones, porque todavía no hay consensos sobre cómo medir la inflación esperada (Cooray, 2003). En este contexto, los estudios que validan dicha hipótesis suelen mostrar correlaciones positivas entre las tasas de interés y la inflación para países desarrollados7. Sin embargo, hay quienes argumentan que dichos hallazgos no son generalizables para los países en desarrollo8.
Los estudios que han tratado de validar las hipótesis de Fisher en su versión internacional y la integración de los mercados tampoco ofrecen evidencia concluyente. Si bien los primeros estudios que analizaron la hipótesis de Fisher sugerían su validez, los estudios contemporáneos no suelen hacerlo, pues suelen argumentar que la existencia de primas de riesgo cambiario son incompatibles con dicha hipótesis (Eiteman, Stonehill y Moffett, 2013), o bien, que los riesgos cambiarios y los costos de transacción internacionales restringen su validación (Hatemi-J, 2009). Por estas razones, los estudios que favorecen las hipótesis mencionadas aceptan que pueden existir grandes desviaciones con respecto a la relación de Fisher postulada.
En la literatura hay varios argumentos que sugieren que las hipótesis de Fisher se cumplen parcialmente debido a cambios estructurales. Quienes defienden esta posición suelen argumentar que los cambios estructurales pueden inducir inestabilidad en las relaciones postuladas (Hatemi-J, 2009). Más aun, suelen argumentar que dichos cambios inducen cambios tecnológicos y en las preferencias, que son los que determinan, en última instancia, las tasas de interés nominales de largo plazo. Los cambios estructurales se suelen atribuir a cambios en las preferencias y en las conductas de los agentes, a desarrollos tecnológicos, a cambios en las políticas e instituciones y a la erupción de crisis económicas y financieras.
Los estudios de las hipótesis de Fisher no suelen incluir análisis de cambio estructural, porque las pruebas para ello todavía se encuentran una fase incipiente de desarrollo. La mayoría de las pruebas existentes consideran que el momento exacto del cambio estructural, o "quiebre", es conocido9; sin embargo, este supuesto es cuestionable en la práctica. Por esta razón, desde hace décadas ha habido interés por desarrollar pruebas de cambio estructural endógeno (i. e., donde el momento del quiebre es desconocido). Aunque la más conocida es la desarrollada por Zivot y Andrews (1992), no se ha utilizado en ninguno de los estudios que han estudiado las hipótesis de Fisher para Latinoamérica10.
Como se ha indicado, hay pocos estudios relativos a las hipótesis de Fisher en Latinoamérica. Además, la mayoría se enfocan en analizar la versión doméstica, la cual se valida en Argentina, Brasil, Chile y, a veces, en México11. Los trabajos que estudian a la hipótesis en su versión internacional son mucho menos frecuentes; más aún, no suelen evaluar directamente las relaciones postuladas por las hipótesis de Fisher. Entre estos últimos se encuentran los de Barquero y Muñoz (2015) y Ruiz y Anguiano (2016), que analizan a Costa Rica y México, respectivamente. Los resultados sugieren que la hipótesis tiende a cumplirse solo en Costa Rica.
La escasez de estudios referidos a las hipótesis de Fisher para los países latinoamericanos puede explicarse por diversas razones: en primer lugar, hasta hace relativamente pocos años, la disponibilidad de series internacionalmente comparables y para periodos relativamente extensos había sido muy limitada en la región; en segundo lugar, muchos países han tenido niveles muy altos de intervención gubernamental y regímenes cambiarios predominantemente fijos; una tercera razón se vincula a los problemas metodológicos derivados de la existencia de choques internos y externos, crisis y procesos de reforma y ajuste en la región. Todas estas razones limitaron el desarrollo de los mencionados estudios e introdujeron cuestionamientos sobre su validez estadística.
La revisión de los estudios empíricos sugiere algunos lineamientos para estudiar las hipótesis de Fisher en Latinoamérica. Particularmente, la revisión justifica el uso de pruebas de raíces unitarias y de la metodología de cointegración de Johansen (1991). Asimismo, los autores de este estudio justifican el uso de pruebas de cambio estructural endógeno para resolver algunas objeciones que se han planteado con respecto a los estudios existentes. En este contexto, la mayor disponibilidad de series económicas y financieras facilitaría realizar dichos estudios. Además, los estudios mencionados podrían justificarse con base en la consideración de que en las tres últimas décadas se ha reducido la intervención gubernamental y se han flexibilizado los regímenes cambiarios de la región.
Finalmente, no sobra enfatizar que el estudio de la validez de las hipótesis de Fisher y, por añadidura, de la integración de los mercados se justifica por razones económicas, financieras y metodológicas. El estudio se justifica, en primer lugar, por las implicaciones vinculadas a las hipótesis analizadas, así como en términos de la mayor liberalización de los mercados de la región. Asimismo, se justifica en términos de la necesidad de entender los tipos de cambio, las tasas de interés y los precios en Latinoamérica. Se enfatizan estas consideraciones por cuanto insertan este estudio dentro de la literatura sobre las relaciones económicas y financieras de la región y porque motivan el desarrollo aquí presentado.
METODOLOGÍA DE ANÁLISIS
En este estudio se analizan las series mensuales de las tasas de interés, los tipos de cambio y los precios de seis países latinoamericanos mediante un enfoque de series de tiempo. La metodología del estudio se sustenta en análisis de tipo estadístico, de cambio estructural y de cointegración. Así, el análisis estadístico se usa para caracterizar las series y sus relaciones entre sí; el análisis de cambio estructural se usa para determinar endógenamente si hay "quiebres" (i. e., cambios estructurales) en las series; el análisis de cointegración se usa para evaluar la existencia de relaciones de largo plazo. Los valores de las series analizadas (i. e., las series en niveles) son aquellos de los logaritmos naturales de las variables originales.
El análisis estadístico se sustenta en estadísticas descriptivas, pruebas de normalidad y correlaciones pairwise. Las estadísticas descriptivas y las pruebas de normalidad de Jarque-Bera se usan para caracterizar el comportamiento de corto plazo de las series en niveles, en tanto las correlaciones pairwise se utilizan para cuantificar las asociaciones lineales de las series y su significancia estadística. Estas correlaciones se estiman para las series de cada uno de los países y para las series de tipos de cambio, tasas de interés y precios, con lo cual se puede mostrar una primera aproximación hacia el análisis de las hipótesis analizadas. En este contexto, cabe señalar que se reportan los p-values de las pruebas de Jarque-Bera y de las correlaciones pairwise para facilitar el análisis estadístico.
El análisis de cointegración requiere que las series analizadas sean integradas de orden uno, I(1) (i. e., deben tener una raíz unitaria). Por esta razón, aquí se usa la prueba aumentada de Dickey-Fuller (ADF) sobre las series en niveles y en diferencias de cada variable. Esta prueba se hace repetidamente, para lo cual se asumen diferentes supuestos que permitan determinar el orden de integración de la series de manera robusta. La hipótesis nula de la prueba ADF es que la serie analizada tiene una raíz unitaria; la alternativa es que la serie sea estacionaria, I(0). Conviene señalar que el análisis de orden de integración también permite validar las relaciones halladas mediante las correlaciones pairwise. Estas relaciones solo son válidas en el largo plazo cuando las series en la regresión son I(0).
El análisis de cambio estructural endógeno complementa el análisis del orden de integración de las series. Este análisis se usa para evaluar endógenamente la existencia de un quiebre en una serie considerada como I(1). Para ello, tal como se ha indicado, se usa la prueba Zivot-Andrews (ZA), que se utiliza repetidamente sobre las series para determinar el momento de ocurrencia de un posible cambio estructural (Zivot y Andrews, 1992)12. Asimismo, la prueba se estima asumiendo diferentes supuestos para obtener estimaciones robustas13. La hipótesis nula de la prueba es que la serie tiene una raíz unitaria y que no experimenta ningún quiebre. La hipótesis alternativa es que la serie es estacionaria y que sí experimenta un quiebre.
En este estudio se evalúa la existencia de movimientos conjuntos y equilibrios de largo plazo mediante la metodología de Johansen (1991), la cual permite evaluar la existencia de relaciones de cointegración (i. e., relaciones de largo plazo) para grupos de series I(1). Para ello, la metodología requiere la estimación de los estadísticos de la traza y del máximo eigenvalor. Las pruebas de cointegración se basan en dichos estadísticos. Al igual que en los análisis anteriores, las pruebas se hacen repetidamente para cada grupo de series analizado, a través de cinco conjuntos de supuestos estadísticos distintos. La hipótesis nula de las pruebas es que no existen relaciones de cointegración en el grupo de series analizado.
Las hipótesis de Fisher y de integración de los mercados de la región se evalúan mediante la contabilización de las relaciones de cointegración existentes, agrupando las series en tres categorías de análisis. Estas categorías permiten definir grupos de series que tienen características comunes. Particularmente, la primera categoría permite identificar y contabilizar las relaciones de cointegración para cada país analizado (seis grupos). La segunda categoría permite identificar y contabilizar las relaciones de cointegración para binomios de países que supuestamente mantienen relaciones bilaterales (quince grupos). La tercera categoría permite identificar y contabilizar las relaciones existentes cuando las series son de un mismo tipo (tres grupos).
La validación empírica de las hipótesis de Fisher requiere que existan relaciones de largo plazo (i. e., relaciones de cointegración) entre los grupos de series analizadas. Particularmente, el grado de integración de las series referidas a cada hipótesis se cuantifica mediante porcentajes, los cuales muestran las relaciones de cointegración contabilizadas de un grupo de series con respecto al máximo de relaciones posibles. Para los grupos que evalúan las hipótesis en su versión doméstica e internacional, estos números son dos y cinco, respectivamente14. Las relaciones contabilizadas son aquellas obtenidas mediante las pruebas de cointegración que muestran una mejor bondad de ajuste y son determinadas mediante el criterio de información de Schwartz.
La metodología de Johansen (1991) también permite estudiar la integración de largo plazo de los mercados financieros de la región. La integración tiende a inducir eficiencia en los mercados y a reducir las oportunidades de arbitraje internacional. En este estudio se valida la integración de los mercados mediante la contabilización de relaciones de cointegración cuando las series analizadas son de un mismo tipo (tipos de cambio, tasas de interés, precios). El grado de integración se mide estimando el porcentaje de las relaciones contabilizadas con respecto al total de relaciones posibles para cada grupo de series. Así, un porcentaje elevado se vincularía a un alto grado de integración de los mercados financieros de largo plazo.
En términos metodológicos, la propuesta de investigación usada en este estudio tiene algunas limitaciones analíticas. Las principales se refieren a los criterios de validación de las hipótesis y a los supuestos que definen las variables esperadas. Particularmente, puede argumentarse que la existencia de relaciones de cointegración es una condición necesaria, pero no suficiente, para validar las hipótesis de Fisher, por cuanto se hace caso omiso de los signos de las correlaciones de largo plazo. Además, puede argumentarse que equiparar las variables nominales corrientes con las esperadas es un supuesto cuestionable. Por estas razones, la evaluación econométrica puede ser considerada como relativamente flexible y a favor de la validez de las hipótesis analizadas.
Finalmente, debe enfatizarse que la metodología propuesta en este estudio tiene cuatro objetivos: a) caracterizar las series de los tipos de cambio, las tasas de interés y los precios en los países analizados; b) determinar endógenamente si ha habido cambios estructurales en dichas variables; c) evaluar la existencia de relaciones de largo plazo, tal como se postula en las hipótesis de Fisher, y de integración de los mercados; d) cuantificar la validez de las hipótesis mencionadas. Estos objetivos son importantes para resolver algunas controversias existentes y para entender las dinámicas de las series latinoamericanas durante las primeras décadas del siglo XXI.
BASE DE DATOS Y ANÁLISIS ESTADÍSTICO DE ORDEN DE INTEGRACIÓN Y CAMBIO ESTRUCTURAL
En este estudio se utilizan series mensuales de los tipos de cambio, las tasas de interés y los precios de Brasil, Chile, Colombia, Costa Rica, México y Perú entre enero de 1997 y diciembre de 2014. Las series usadas son aquellas para las que existen datos completos para el periodo. Por convención, las series en niveles transforman las variables originales en términos del logaritmo natural del valor nominal V de la variable i en el mes t, lnV it. Las series en diferencias miden las variaciones mensuales de las variables (r it = lnV it -lnV it-1 ). Así, la base de datos incluye un total de 18 series en niveles y 18 series en diferencias. Particularmente, cada serie en niveles incluye 216 observaciones. La tabla 1 muestra las variables originales usadas en el estudio.
Tabla 1 Variables usadas en el estudio
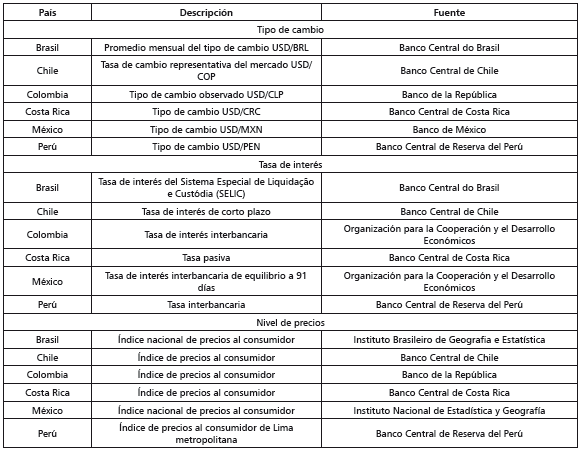
Nota: las series de las variables son de periodicidad mensual. En el caso de fuentes con mayor periodicidad, se toma la última observación del mes. Las series de índices de precios toman como base diciembre de 2010.
Fuente: elaboración de los autores.
La tabla 2, por su parte, muestra la estadística descriptiva de las series en niveles durante el periodo analizado. Particularmente, la evidencia muestra que, en promedio, las tasas de interés de Chile han sido las más bajas y que las de Brasil han sido las más altas. Asimismo, las desviaciones estándar muestran que los tipos de cambio de Perú han sido los más estables y que los de Brasil han sido los más volátiles; más aún, se evidencia que los precios de Perú han sido los más estables y que los de Costa Rica han sido los más volátiles. La evidencia también muestra que once series exhiben un sesgo positivo, en tanto las restantes tienen un sesgo negativo. Asimismo, las pruebas de Jarque-Bera muestran que sólo hay seis series distribuidas normalmente (usando un nivel de significancia del 1%).
Tabla 2 Estadística descriptiva de las series en niveles y pruebas de Jarque-Bera
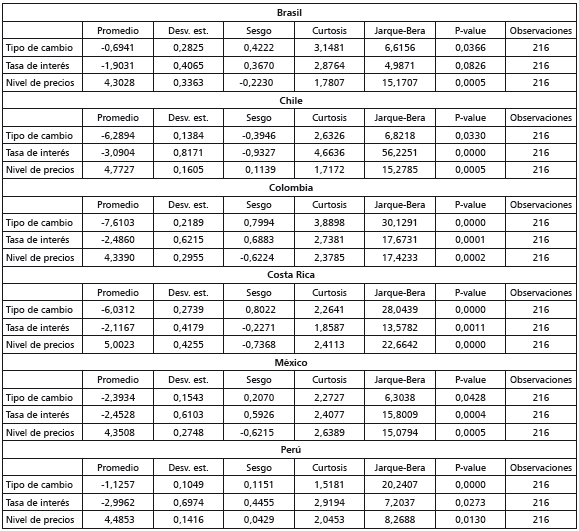
Nota: las series en niveles expresan en términos de logaritmos naturales los valores de las variables originales.
Fuente: elaboración de los autores.
La tabla 3 muestra las correlaciones pairwise para las series de los países analizados; no obstante, hay escasa evidencia que confirme las correlaciones postuladas por las hipótesis de Fisher. La tabla muestra que solo en Chile y Costa Rica hay correlaciones significativas y positivas entre las tasas de interés y los precios, al igual que siempre hay correlaciones positivas y significativas entre las tasas de interés y los tipos de cambio. Por tanto, la evidencia sugiere que las correlaciones postuladas por la hipótesis de Fisher en su versión internacional no ocurren en ningún caso, al menos en el corto plazo15. La tabla 3 también permite identificar que en Costa Rica y Perú las apreciaciones de la moneda coinciden con incrementos en los niveles de precios.
Tabla 3 Correlaciones pairwise de las series en niveles de las economías latinoamericanas
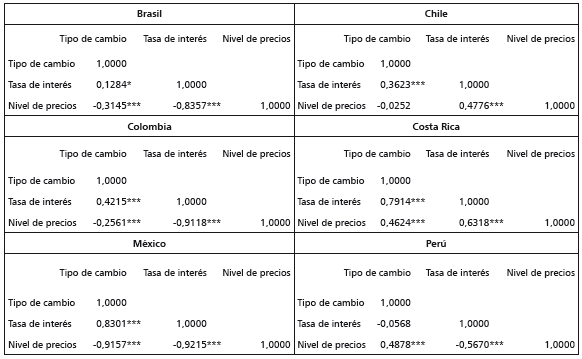
Nota: las series en niveles expresan en términos de logaritmos naturales los valores de las variables originales. Uno, dos y tres asteriscos denotan niveles de significancia del 10%, 5% y 1%, respectivamente.
Fuente: elaboración de los autores.
La tabla 4 muestra las correlaciones pairwise para series de un mismo tipo y que hay correlaciones positivas y significativas entre los tipos de cambio y entre las tasas de interés de los países latinoamericanos16. Así, la evidencia sugiere que los tipos de cambio y las tasas de interés tienden a moverse conjuntamente entre sí, al menos en el corto plazo, al igual que los precios tienden a exhibir correlaciones significativas. Sin embargo, la existencia de correlaciones positivas y negativas sugiere que no hay movimientos comunes en las dinámicas de corto plazo de los precios. Así, la evidencia sugiere que las dinámicas de los precios son heterogéneas entre los países de la región.
Tabla 4 Correlaciones pairwise para las series en niveles por tipo de variable
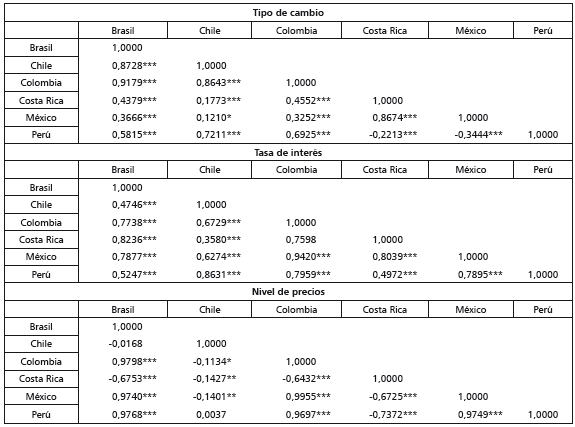
Nota: las series en niveles expresan en términos de logaritmos naturales los valores de las variables originales. Uno, dos y tres asteriscos denotan niveles de significancia del 10%, 5% y 1%, respectivamente.
Fuente: elaboración de los autores.
La tabla 5 muestra las estimaciones de las pruebas ADF usando los tres conjuntos de supuestos estadísticos considerados. La tabla sugiere que todas las series en niveles son integradas de orden uno, I(1). Estos resultados avalan, en principio, que dichas series son elegibles para el análisis de cointegración y que los resultados obtenidos mediante las correlaciones pairwise son, hasta cierto punto, cuestionables17. Incluso, desde una perspectiva económico-financiera, los resultados también indican que hay cierto grado de eficiencia en los mercados de la región. Ello, en virtud de que la hipótesis de eficiencia de los mercados supone la imposibilidad de poder predecir el comportamiento de las series de manera consistente en el largo plazo (Fama, 1970).
Tabla 5 Pruebas ADF para las series en niveles y en diferencias
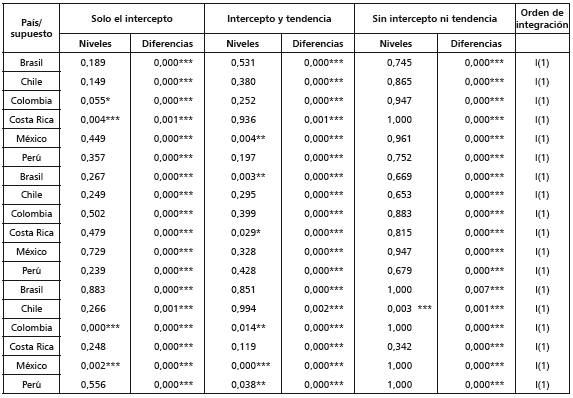
Nota: las series en niveles expresan en términos de logaritmos naturales los valores de las variables originales. Las series en diferencias expresan las tasas de crecimiento mensual de las variables. Los supuestos se refieren a las variables exógenas incluidas en la regresión de la prueba ADF. El análisis de orden de integración prioriza el supuesto ninguno (sin intercepto ni tendencia). Uno, dos y tres asteriscos denotan niveles de significancia del 10%, 5% y 1%, respectivamente.
Fuente: elaboración de los autores.
La tabla 6 muestra las estimaciones de las pruebas ZA usando los tres grupos de supuestos estadísticos considerados para cada una de las series. La evidencia sugiere la existencia de que hubo, al menos, un quiebre en nueve de las series durante el periodo analizado18. Particularmente, los tipos de cambio de México aparentemente tuvieron quiebres en 2003 y 2008. Las tasas de interés de Brasil, Costa Rica y Perú parecen haber tenido quiebres, respectivamente, en 2012, 2006 y 2001. Los precios de Brasil, Colombia, Costa Rica, México y Perú parecen haber tenido quiebres, respectivamente, en 2002, 2008, 2009, 1999 y 200119. Por tanto, la evidencia sugiere que solo Chile no experimentó ningún tipo de cambio estructural.
Tabla 6 Pruebas ZA para las series en niveles
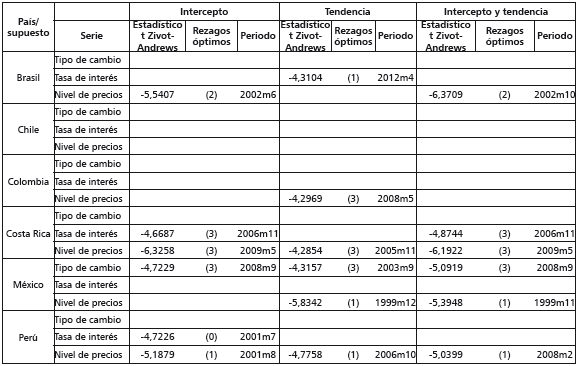
Nota: las series en niveles expresan en términos de logaritmos naturales los valores de las variables originales. Los supuestos se refieren a la localización del quiebre en la prueba ZA. El número óptimo de rezagos se determina mediante el criterio de la t-secuencial. Los estadísticos, rezagos y periodos reportados refieren posibles quiebres en las series. El nivel de significancia considerado en las pruebas es del 10%. El número de rezagos óptimo se muestra entre paréntesis. El estadístico t asociado a cada supuesto corresponde con el rechazo de la hipótesis nula. Ho es la serie en cuestión que presenta raíz unitaria sin cambio estructural. H1 es la serie en cuestión que presenta un proceso estacionario (en tendencia, intercepto o ambos) con un posible cambio estructural.
Fuente: elaboración de los autores.
Los resultados combinados de los análisis de correlación pairwise, de raíz unitaria y de cambio estructural confirman que hay escasa evidencia que confirme las correlaciones de largo plazo postuladas por las hipótesis de Fisher. Los resultados sugieren que la correlación postulada en su versión doméstica solo se cumple para Costa Rica en el corto plazo (tasas de interés y precios correlacionados positivamente). En Chile, Colombia y México, la evidencia no es consistente, debido a que la mayoría de las series de tasas de interés y de precios exhiben raíces unitarias y cambios estructurales. Se hace énfasis en estos factores porque también se manifiestan en los tipos de cambio. Por estas razones, en principio, las correlaciones postuladas por la hipótesis en su versión internacional no pueden confirmarse en ninguno de los países analizados.
Finalmente, los resultados de esta sección pueden sintetizarse de la siguiente manera: a) durante el periodo analizado, las tasas de interés de Chile han sido las más bajas y las de Brasil han sido las más altas; b) los tipos de cambio de Perú han sido los más estables y los de Brasil han sido los más volátiles; c) los precios de Perú han sido los más estables y los de Costa Rica han sido los más volátiles; d) hay evidencia de cambios estructurales en, al menos, nueve series; e) únicamente Chile no experimentó ningún tipo de cambio estructural; f) la correlación postulada por la hipótesis de Fisher en su versión doméstica solo se cumple para Costa Rica, y g) hay escasa evidencia que confirme las correlaciones de largo plazo postuladas por las hipótesis de Fisher.
ANÁLISIS DE COINTEGRACIÓN
En esta sección se evalúa la validez de las hipótesis de Fisher y de la integración de los mercados latinoamericanos. Estas evaluaciones se sustentan en el uso repetido de la metodología de Johansen para contabilizar las relaciones de cointegración en distintos grupos de series20. Particularmente, la hipótesis de Fisher en su versión doméstica se evalúa analizando los grupos de series nacionales. Por su parte, la hipótesis de Fisher en su versión internacional se evalúa mediante el análisis las series de los países que mantienen relaciones bilaterales. La hipótesis de la integración de los mercados se evalúa analizando los grupos de series del mismo tipo. Por simplicidad, los resultados de las estimaciones se muestran en las tablas 7, 8, 9 y 10.
Tabla 7 Relaciones de cointegración en las series de los países latinoamericanos
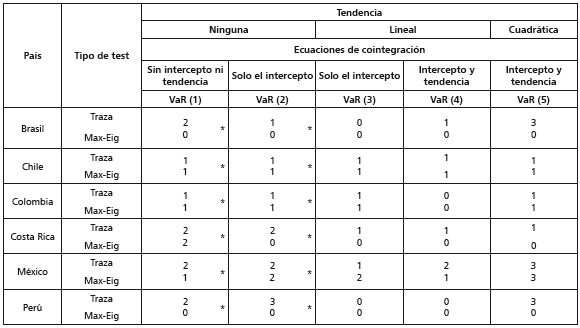
Nota: las series en niveles expresan en términos de logaritmos naturales los valores de las variables originales. Las relaciones de cointegración se estiman para los seis grupos de series nacionales usando los distintos supuestos de especificación de la tendencia de los datos y de las ecuaciones de cointegración. Cada grupo analizado incluye las tres series de un país. Un asterisco denota los mejores supuestos para analizar las relaciones de cointegración para un grupo de series, según el criterio de información de Schwartz. Las relaciones de cointegración se estiman usando: a) un intervalo de 12 rezagos para los modelos VaR, b) los p-values propuestos por MacKinnon, Haug y Michelis (1999) y c) un nivel de significancia del 10%.
Fuente: elaboración de los autores.
Tabla 8 Relaciones de cointegración en las series de los países latinoamericanos que mantienen relaciones bilaterales
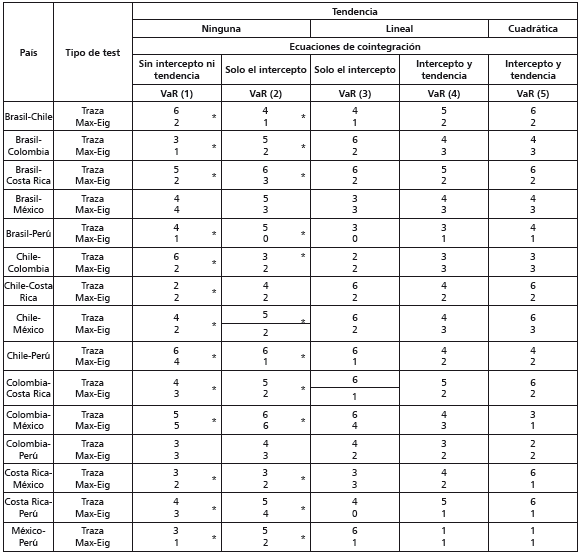
Nota: las series en niveles expresan en términos de logaritmos naturales los valores de las variables originales. Las relaciones de cointegración se estiman para los quince grupos de series usando los distintos supuestos de especificación de la tendencia de los datos y de las ecuaciones de cointegración. Cada grupo analizado incluye las seis series de las economías que mantienen relaciones bilaterales. Un asterisco denota los mejores supuestos para analizar las relaciones de cointegración para un grupo de series, según el criterio de información de Schwartz. Las relaciones de cointegración se estiman usando: a) un intervalo de 12 rezagos para los modelos VaR, b) los p-values propuestos por MacKinnon, Haug y Michelis (1999) y c) un nivel de significancia del 10%.
Fuente: elaboración de los autores.
Tabla 9 Relaciones de cointegración en las series latinoamericanas de mercados similares
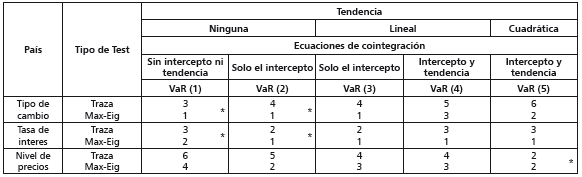
Notas: las series en niveles expresan en términos de logaritmos naturales los valores de las variables originales. Las relaciones de cointegración se estiman para los tres grupos de series usando los distintos supuestos de especificación de la tendencia de los datos y de las ecuaciones de cointegración. Cada grupo analizado incluye las seis series del mismo tipo. Un asterisco denota los mejores supuestos para analizar las relaciones de cointegración para un grupo de series, según el criterio de información de Schwartz. Las relaciones de cointegración se estiman usando: a) un intervalo de 12 rezagos para los modelos VaR, b) los p-values propuestos por MacKinnon, Haug y Michelis (1999) y c) un nivel de significancia del 10%.
Fuente: elaboración de los autores.
Tabla 10 Números y porcentajes de relaciones contabilizadas por grupo de series
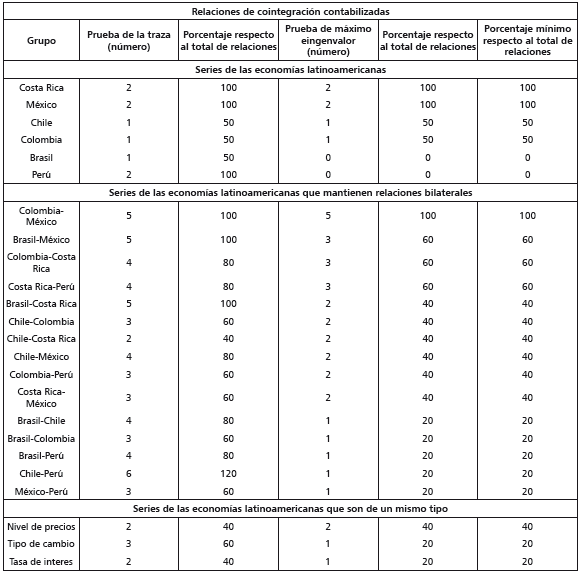
Nota: las relaciones de cointegración registradas son aquellas que se vinculan a los mejores supuestos para analizar las relaciones de cointegración, de acuerdo con las tablas 7, 8 y 9. Se registran los valores dados por la traza y máximo eigenvalor cuando los números de relaciones coinciden y cuando hay una bondad de ajuste similar para supuestos distintos. Si hay diferencias en los números de relaciones, se registran los valores mínimos asociados a la suma de la traza y el máximo eigenvalor. Los porcentajes son estimados con base en las relaciones contabilizadas con respecto al total de relaciones posible en cada grupo. Las relaciones de cointegración se estiman usando: a) un intervalo de 12 rezagos para los modelos VaR1; b) los p-values propuestos por MacKinnon, Haug y Michelis (1999); y c) un nivel de significancia del 10%.
Fuente: elaboración de los autores.
La tabla 7 sintetiza los resultados de las pruebas de cointegración para las series de cada uno de los países latinoamericanos. Estos resultados muestran que la mayoría de las series nacionales tienen movimientos y equilibrios comunes de largo plazo21. Particularmente, la tabla muestra que hay cointegración en las series de Chile, Colombia, Costa Rica y México. Sin embargo, si se consideran los resultados de la sección anterior, la evidencia tiende a validar débilmente la hipótesis de Fisher en su versión doméstica principalmente para Costa Rica. Los resultados de las pruebas de cointegración también pueden interpretarse en términos de que resultaría viable realizar operaciones de arbitraje exitosas y de largo plazo usando activos brasileños o peruanos.
La tabla 7 también sugiere que las series nacionales no están integradas de la misma manera en el interior de los países de la región. Esta afirmación se sustenta con base en la contabilización de las relaciones de cointegración existentes para las series de cada país. Particularmente, en Costa Rica y México, el grado integración de los mercados nacionales es del 100%, en tanto en Chile y Colombia este se reduce a un 50%. Por tanto, si bien la evidencia muestra que hay cointegración en el ámbito nacional, también muestra que las variables económicas y financieras nacionales pueden tener dinámicas independientes de corto y largo plazos.
La tabla 8 sintetiza los resultados de las pruebas de cointegración de los binomios de países que mantienen relaciones bilaterales. Estos resultados confirman que hay movimientos y equilibrios comunes de largo plazo. Sin embargo, las pruebas de cointegración de la traza y del máximo eigenvalor estiman números de relaciones de cointegración diferentes para la mayoría de grupos de series. Los únicos grupos para los cuales hay coincidencias se refieren a los binomios Chile-Costa Rica y Colombia-México; por tanto, la tabla sugiere que hay evidencia débil en favor del cumplimiento de la hipótesis de Fisher en su versión internacional principalmente para dichos binomios de países.
La tabla 8 también muestra el grado de integración de los mercados latinoamericanos cuando hay relaciones bilaterales en los países de la región. Particularmente, el binomio Colombia-México destaca porque el grado integración de los mercados es del 100%. El binomio Chile-Costa Rica, por su parte, tiene un grado de integración del 40%. En lo que se refiere a los otros binomios analizados, la evidencia tiende a apoyar la integración de los mercados. Sin embargo, la falta de coincidencia en las contabilizaciones dificulta evaluar la validez referida a dichos binomios, situación que sugiere heterogeneidad en las relaciones bilaterales de los países latinoamericanos.
La tabla 9 sintetiza los resultados de las pruebas de cointegración para las series de los mercados latinoamericanos. Aunque estos confirman que hay movimientos y equilibrios comunes de largo plazo en los mercados de la región, las pruebas de cointegración de la traza y del máximo eigenvalor estiman números de relaciones de cointegración diferentes para las series de las tasas de interés y los tipos de cambio. El único grupo que registra coincidencias en los números es el que incluye series de precios; por tanto, la tabla sugiere que si bien hay evidencia en favor de la integración de los mercados latinoamericanos, esta se refleja principalmente en los mercados de bienes y servicios.
La tabla 9 también sugiere que los mercados latinoamericanos están integrados de una manera parcial y heterogénea. Esta afirmación se sustenta con base en la contabilización de las relaciones de cointegración existentes en los tres grupos de series. Particularmente, en el mercado de bienes y servicios el resultado de integración es del 40%. En lo que se refiere a los mercados monetarios y cambiarios, nuevamente la falta de coincidencia en las contabilizaciones de las relaciones de cointegración dificulta evaluar los porcentajes de integración de estos. Esta situación muestra que las políticas monetarias y cambiarias han tendido a ser independientes en la región latinoamericana.
La tabla 10 sintetiza la información relativa a las relaciones de cointegración contabilizadas vinculadas a los mejores supuestos de especificación determinados en las tablas 7, 8 y 9. La información se ordena de mayor a menor, con base en los porcentajes de relaciones contabilizadas con respecto al total de relaciones posibles para cada grupo. Los resultados mostrados en la tabla sugieren que hay oportunidades para consolidar la integración financiera en la mayoría de los países y mercados latinoamericanos. Particularmente, indican que la mayoría de dichas oportunidades se ubican en Brasil y Perú y en los mercados cambiarios y monetarios. Además, la tabla muestra que Costa Rica tiene los mayores niveles de integración nacional e internacional.
Finalmente, los resultados del análisis de cointegración pueden sintetizarse de la siguiente manera: a) hay movimientos y equilibrios comunes de largo plazo en las series; b) la hipótesis de Fisher, en su versión doméstica, tiende a validarse principalmente en Costa Rica; c) la hipótesis de Fisher, en su versión internacional, tiende a validarse débilmente en las relaciones bilaterales entre Chile y Costa Rica y entre Colombia y México; d) la integración financiera de los países y mercados latinoamericanos tiende a ser muy heterogénea; e) hay evidencia en favor de la integración de los mercados latinoamericanos de bienes y servicios, y f) hay oportunidades para consolidar la integración de los mercados en Brasil y Perú y en los mercados cambiarios y monetarios de la región.
CONCLUSIONES Y DISCUSIÓN
En este estudio se ha evaluado las hipótesis de Fisher y de integración de los mercados latinoamericanos Estas evaluaciones se han sustentado en la metodología de cointegración de Johansen (1991). Así, se han estudiado: a) el comportamiento de las series de tipos de cambio, tasas de interés y precios; b) la existencia de cambios estructurales en las series; c) las relaciones de largo plazo de las series, y d) la validez de las hipótesis analizadas. El estudio ha utilizado estadísticas descriptivas, correlaciones pairwise y pruebas de raíz unitaria, de cambio estructural endógeno y de cointegración. La base de datos analizada ha incluido series mensuales de Brasil, Chile, Colombia, Costa Rica, México y Perú para el periodo de enero de 1997 a diciembre de 2014.
Los hallazgos de los análisis estadístico, de raíces unitarias y de cambio estructural pueden sintetizarse de la siguiente manera: a) durante el periodo analizado, las tasas de interés de Chile han sido las más bajas y las de Brasil han sido las más altas; b) los tipos de cambio de Perú han sido los más estables y los de Brasil han sido los más volátiles; c) los precios de Perú han sido los más estables y los de Costa Rica han sido los más volátiles; d) hay evidencia de cambios estructurales en, al menos, nueve series; e) únicamente Chile no experimentó ningún cambio estructural; f) la correlación postulada por la hipótesis de Fisher en su versión doméstica solo se cumple en Costa Rica, y g) hay escasa evidencia que confirme las correlaciones postuladas por las hipótesis de Fisher.
Los hallazgos de los análisis de cointegración pueden sintetizarse de la siguiente manera: a) hay movimientos y equilibrios comunes de largo plazo en las series; b) la hipótesis de Fisher, en su versión doméstica, tiende a validarse principalmente en Costa Rica; c) la hipótesis de Fisher, en su versión internacional, tiende a validarse débilmente en las relaciones bilaterales entre Chile y Costa Rica y entre Colombia y México; d) la integración financiera de los países y mercados latinoamericanos tiende a ser muy heterogénea; e) hay evidencia en favor de la integración de los mercados latinoamericanos de bienes y servicios, y f) hay oportunidades para consolidar la integración de los mercados en Brasil y Perú y en los mercados cambiarios y monetarios de la región.
Los resultados del estudio implican que la validez de las hipótesis de Fisher y de la integración de los mercados es muy limitada en Latinoamérica; más aún, sugieren que los mercados no siempre están en equilibrio, que son ineficientes y proveen oportunidades de cobertura, diversificación y arbitraje. Estas conclusiones son especialmente relevantes para la formulación de políticas económicas y financieras. La escasa integración de las tasas de interés nominales y de los tipos de cambio justifica su utilidad como instrumentos de política al menos en el corto plazo y, más aún, validan las hipótesis de que el dinero no es neutral en la economía y que los agentes no son neutrales al riesgo.
Los resultados relativos a la escasa validez de las hipótesis de Fisher en Latinoamérica pueden explicarse por diversas razones. La hipótesis en su versión doméstica pudo haber sido no validada, en buena medida, debido al escaso desarrollo de los mercados financieros y por la existencia de restricciones a los movimientos de capitales de la región. Por su parte, la hipótesis en su versión internacional pudo haber sido no validada debido a la existencia de inconsistencias en la flexibilidad de los regímenes cambiarios. La existencia de cambios estructurales en las series de tipo de cambio de Brasil, Costa Rica y Perú sugiere que hubo cambios significativos en los regímenes cambiarios de dichos países22.
En términos analíticos, la evidencia también indica que hay vínculos entre la integración de los mercados y los cambios estructurales de la región. Estos vínculos son, en principio, particularmente notorios en las series de precios, que son las que contabilizan los mayores porcentajes de relaciones de cointegración y son también las que registran el mayor número de cambios estructurales. Esta situación podría interpretarse en términos de que las series económicas y financieras y la integración de los mercados tienden a correlacionarse cuando hay cambios estructurales. Si bien hay estudios empíricos que sugieren la validez de dicha vinculación, debe reconocerse que la evidencia presentada aquí no es concluyente23.
Finalmente, debe enfatizarse que la investigación empírica referida a los tipos de cambio, las tasas de interés y los precios tiene amplias posibilidades de desarrollo. En los países latinoamericanos, la importancia de este tipo de investigación se vincula con las relaciones económicas internacionales, el desarrollo económico y la estabilidad financiera de la región. Esto ocurre porque los comportamientos de dichas variables, si bien reflejan las acciones públicas y privadas y los impactos de choques internos y externos, también determinan las expectativas y decisiones de los agentes nacionales e internacionales. En este contexto, la importancia de realizar nuevas investigaciones quedaría justificada por razones de interés público y privado.