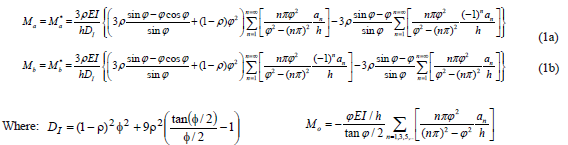
MOMENTOS INDUCIDOS Y DEFLEXIONES LATERALES EN COLUMNAS CON IMPERFECCIONES INICIALES Y CONEXIONES SEMIRIGIDAS: II. VERIFICACIÓN Y EJEMPLOS
J. DARIO ARISTIZABAL-OCHOA
Ph.D. School of Mines, National University, Medellin, Colombia, jdaristi@unal.edu.co
Received for review November 11th, 2011, accepted February 9th, 2012, final version February, 12th, 2012
ABSTRACT: An analytical method and the closed-form expressions derived in a companion paper are used to evaluate the induced elastic bending moments and second-order deflections in slender prismatic columns with initial geometric imperfections (i.e., initial curvature and out-of-plumbness) and semirigid connections when the columns are subjected to eccentric axial loads at both ends. Comparisons of the induced elastic moments, the second-order deflections, and the critical loads obtained using the proposed approach, and those available in the technical literature for classic column cases are presented herein. Also, sensitivity studies and several examples are presented in detail which demonstrate the effectiveness and accuracy of the proposed closed-form equations and the importance of initial imperfections, semirigid connections, and lateral bracing on the second-order behavior and stability of beam-columns. Results obtained from the proposed equations are compared with those obtained using the FEM computer program ABAQUS, showing its simplicity and accuracy. The closed-form expressions can be used by researchers and structural engineers to investigate the effects of initial imperfections and semirigid connections on the elastic behavior of columns under heavy eccentric axial loads, including cases with relatively large deflections (< 0.1 times the column span).
KEY WORDS: Beam-columns, bracing, buckling, columns, computer applications, deflections, design, frames, large deflections, loads, reversals of deflections, second-order analysis, stability
]]> RESUMEN: Un método analítico y expresiones cerradas derivadas en una publicación adjunta son utilizadas para evaluar los momentos de flexión y deformaciones laterales elásticas de segundo-orden inducidas en columnas prismáticas esbeltas con conexiones semirrígidas y con imperfecciones iníciales geométricas (tales como curvatura y desplome iníciales) cuando son sometidas a fuerzas axiales excéntricas en ambos extremos. En esta publicación se presentan comparaciones de los momentos inducidos y las deformaciones de segundo-orden y las cargas críticas obtenidas utilizando el método propuesto con los otros métodos disponibles en la literatura técnica para los casos clásicos de columnas aisladas. También se presenta en detalle estudios de sensibilidad y ejemplos que demuestran la eficacia y la precisión del método propuesto y de sus ecuaciones cerradas mostrando la importancia de los efectos de las imperfecciones iníciales, conexiones semirrígidas y arriostramiento lateral en el análisis de segundo-orden y la estabilidad de vigas-columnas. Resultados obtenidos a partir del método propuesto y de sus ecuaciones y comparaciones con los obtenidos con el programa ABAQUS de elementos finitos. Investigadores e ingenieros estructurales pueden utilizar el método propuesto para estudiar los efectos combinados de las imperfecciones iniciales y las conexiones semirrígidas en el comportamiento elástico de columnas bajo grandes cargas axiales excéntricas incluyendo casos con deformaciones relativamente grandes (<0,1 veces el tamaño de columna).PALABRAS CLAVE: Vigas-columnas, arriostramiento, pandeo, columnas, aplicaciones informáticas, deflexiones, diseño, marcos, grandes deflexiones, cargas, reversión de deflexiones, análisis de segundo-orden, estabilidad
1. INTRODUCTION
The effects of initial imperfections on the elastic response of slender columns subjected to axial loads were investigated by the writer in a companion paper [1].
Formulas that can be used in the analysis of columns that exceed the out-of-straightness and out-of-plumbness tolerated by the construction codes are nonexistent in the technical literature. The main objective of this publication is precisely that, to present closed-form expressions for Euler-Bernoulli columns with uninhibited, partially-inhibited, and totally-inhibited sidesway that can be used in their stability and second-order analyses. Comparisons of the induced elastic moments, second-order deflections and buckling loads obtained using the proposed approach with those available in the technical literature for classical column cases are presented. In addition, sensitive studies carried out using the proposed closed-form expressions and the FEM computer program ABAQUS are presented in detail. These demonstrate the effectiveness and accuracy of the proposed equations and the importance of initial imperfections on the second-order behavior as well as the stability of prismatic columns with semirigid connections and lateral bracing.
2. CLASSIC COLUMN CASES
Closed form expressions developed by Aristizabal-Ochoa listed in Table 1 (see [1]) are used herein to calculate the induced end moments, lateral deflections, and buckling axial loads of classical column cases with initial imperfections.
2.1. Columns with sidesway inhibited
]]> 2.1.1. Column with initial curvature and equal end restraints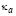 =
= 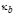 =
= 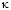 (or
(or 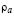 =
= 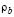 =
= 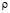 ) are as follows:
) are as follows: 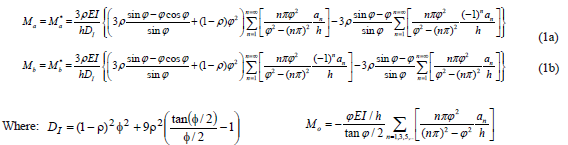
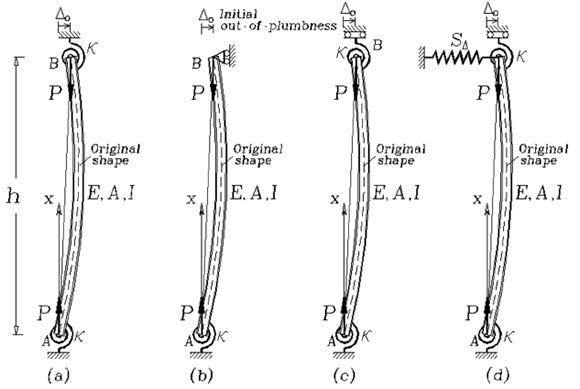
Figure 1. Imperfect column cases analyzed with equations from Table 1 and the FEM program ABAQUS. a) Column with identical rotational restraints and sidesway inhibited; (b) Column hinged at B and with rotational restraint at A and sidesway inhibited; (c) Column with identical rotational restraints and sidesway uninhibited; and (d) Column with identical rotational restraints and sidesway partially inhibited by lateral spring SD
Notice that symmetric buckling occurs only when the initial imperfection is also symmetric (i.e., when n = 1, 3, 5...) with Ma = -Mb = Mo given by Eq. (2):
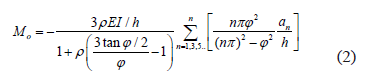
Anti-symmetric buckling occurs only when the initial imperfection is also anti-symmetric (i.e., when n = 2, 4, 6...) with Ma = Mb = Mo given by Eq. (3):
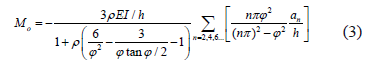
Notice that for 1) r = 0 (i.e., perfectly pinned-pinned column), then from Eqs. (2) and (3), Mo = 0 for both symmetrical and anti-symmetrical buckling modes; 2) r = 1 (i.e., a perfectly clamped-clamped column), then from Eq. (2):
]]>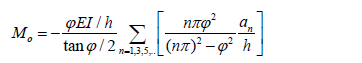
This expression is identical to that reported by Timoshenko and Gere [2] or n = 1 for the symmetrical buckling mode. Likewise, from Eq. (3)
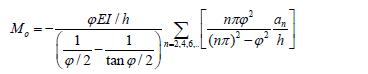
for the anti-symmetrical modes; and 3) the buckling loads for the symmetrical and anti-symmetrical modes can be calculated from the characteristic equations 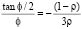 and
and 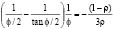 [obtained by making the denominators of Eqs. (2) and (3) equal to zero], respectively. These last two expressions are identical to that reported by Timoshenko and Gere [2].
[obtained by making the denominators of Eqs. (2) and (3) equal to zero], respectively. These last two expressions are identical to that reported by Timoshenko and Gere [2].
The lateral deflection along the column can be obtained from the expressions listed at the bottom of Table 1 for symmetric and anti-symmetric buckling. For instance, for the symmetric case u(x) and u(h/2), these are as follows:
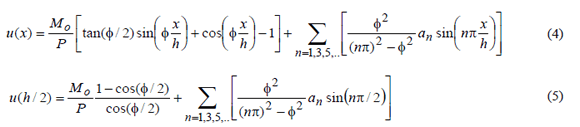
For n = 1 with the maximum moment along the column occurring at mid-span:
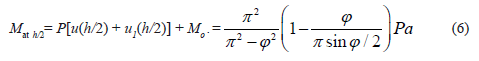
Expressions (5) and (6) are identical to those reported by Timoshenko and Gere [2].
2.1.2. Column with initial curvature and unequal end restraints ]]>
The end moments and the corresponding buckling axial loads of the Fig. 1a column are derived next, assuming that D - D0 = ea = eb = 0 and 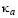 ¹
¹ 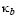 (or
(or 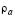 ¹
¹  ) and the results are compared with those presented by Timoshenko and Gere [2].
) and the results are compared with those presented by Timoshenko and Gere [2].
Using Eqs. (2,4, and 5), the end moments Ma and Mb can be calculated directly. Now the buckling loads can be the obtained by making De, given by Eq. (5), equal to zero, obtaining the following characteristic equation:
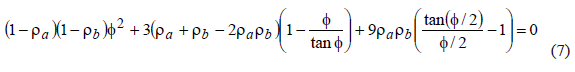
For the particular case of ra = r, rb = 0, the moment at A is reduced to the following expression:
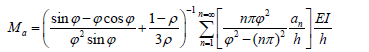
and the characteristic equation is reduced to
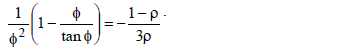
Notice that when: 1) r = 0 (i.e., perfectly pinned-pinned column) Ma = 0; 2) r = 1 (i.e., perfectly clamped-pinned column) then;
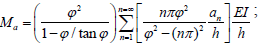
and 3) the buckling loads for all modes can be calculated from the characteristic equation 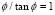 identical to that reported in the technical literature [2]. The bending moment and lateral deflection along the column can be obtained using (6) and (7) making D - D0 = 0.
identical to that reported in the technical literature [2]. The bending moment and lateral deflection along the column can be obtained using (6) and (7) making D - D0 = 0.
For the particular case of columns with different end restraints (ra 1 rb) and SD = 0, the characteristic equation is reduced to
Now, when ea 1 eb, the moments Ma and Mb, and lateral sway obtained using Eq. (6) are as follows:
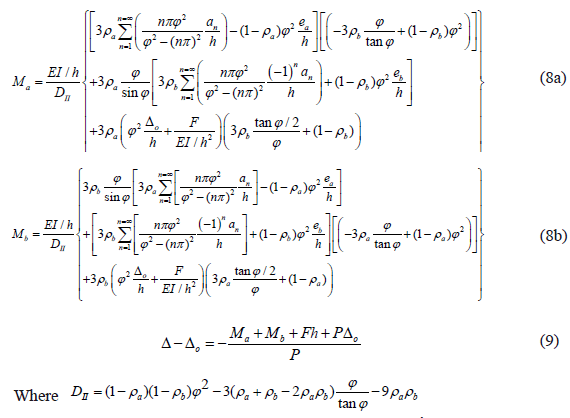
For the particular case of a column with clamped ends (ra = rb = 1), the moments Ma and Mb become
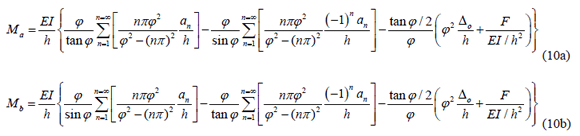
The buckling loads for all modes can be calculated from the characteristic equation 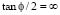 or
or 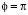 (n = 1, 3, 5...) identical to that which is reported in the technical literature. In the particular case of a cantilever column with
(n = 1, 3, 5...) identical to that which is reported in the technical literature. In the particular case of a cantilever column with 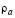 = r and
= r and 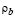 = 0, the end moments and lateral sway are reduced to:
= 0, the end moments and lateral sway are reduced to:
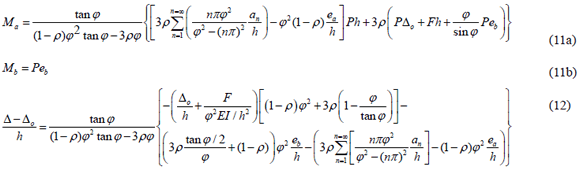
For the particular case of a perfectly clamped cantilever column (i.e., r = 1) with initial imperfections:
]]>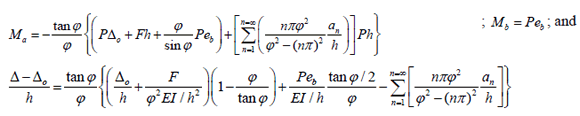
For a perfectly clamped and straight cantilever (i.e., r = 1 and an = 0):
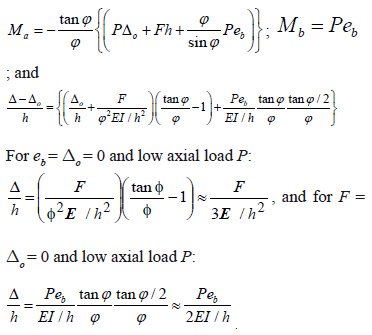
These results are identical to those obtained from a linear elastic (first-order) analysis.
3. SENSITIVITY STUDIES AND VERIFICATION WITH ABAQUS
A series of sensitivity studies were carried to study the variations of the induced moment at end A Ma, the maximum lateral deflection along the span, as well as the ratio Ma/Mmax (i.e., negative moment at end A to the maximum positive moment along the column) for the column cases shown by Figs. 1(a)-(d) as the axial load is increased from zero to critical load (normalized with regard to Pe = p2EI/h2) with the fixity factor r varying from 0 to 1 (i.e., from perfectly-hinged to clamped-end conditions)
Figures 2-9 show these three variations in detail for the slender columns of Fig. 1, with an initial imperfection at midspan of a = h/1000 (assuming sinusoidal and parabolic initial shapes) and out-of-plumb D0= h/500. The four column cases were analyzed using the proposed closed-form expressions listed in Table 1 and the FEM computer program ABAQUS. The FEM model consisted of 300 segments (B22H elements form the ABAQUS library), requiring 500 iterations and about 4 min of CPU time in a standard Pentium 4 PC.
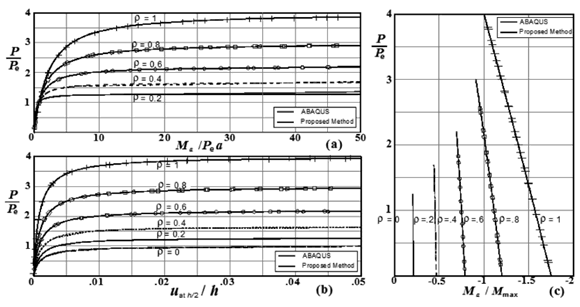
Figure 2. Effects of end fixity on the second-order response of column of Fig. 3a (assuming sinusoidal initial shape with a = h/1000, D0 = h/500). Variations of: (a) Ma/Pea; (b) uat h/2/h); and (c) Ma/Mmax with P/Pe (where Pe = p2EI/h2)
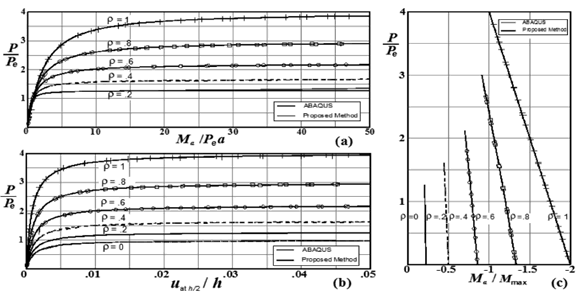
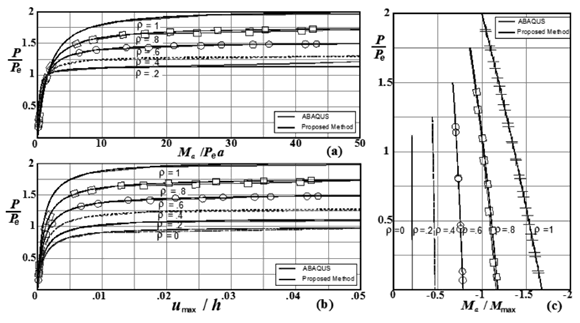
Figure 4. Effects of end fixity on the second-order response of the Fig. 3b column (assuming sinusoidal initial shape with a = h/1000, D0 = h/500). Variations of (a) Ma/Pea; (b) umax/ h); and (c) Ma/Mmax with P/Pe (where Pe = p2EI/h2)
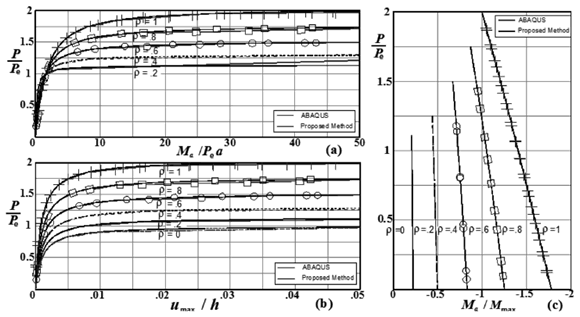
Figure 5. Effects of end fixity on the second-order response of column of Fig. 3b (assuming a parabolic initial shape with a = h/1000, D0 = h/500). Variations of: (a) Ma/Pea; (b) uat h/2/h); and (c) Ma/Mmax with P/Pe (where Pe = p2EI/h2).

Figure 6. Effects of end fixity on the second-order response of the Fig. 3c column (assuming a sinusoidal initial shape with a = h/1000, D0 = h/500). Variations of: (a) Ma/ Pea; (b) (D - D0)/h; and (c) Ma/Mmax with P/Pe (where Pe = p2EI/h2)

Figure 7. Effects of end fixity on the second-order response of the Fig. 3c column (assuming a parabolic initial shape with a = h/1000, D0 = h/500). Variations of: (a) Ma/Pea; (b) (D - D0)/h; and (c) Ma/Mma with P/Pe (where Pe = p2EI/h2)
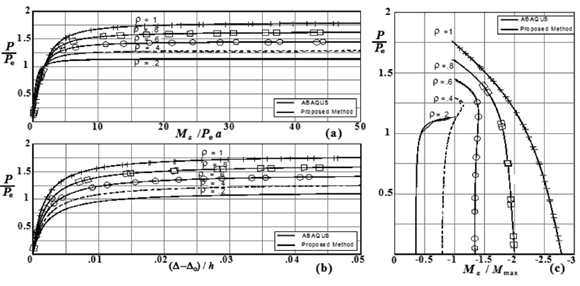
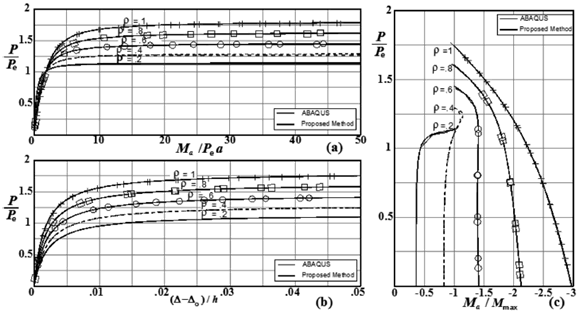
Figure 9. Effects of end fixity on the second-order response of the Fig. 3d column (assuming a parabolic initial shape with a = h/1000, D0 = h/500, and SD = 10EI/h3). Variations of: (a) Ma/Pea; (b) uat h/2/h; and (c) Ma/Mmax. with P/Pe (where Pe = p2EI/h2).
Based on the results shown in Figs. 2-5 for columns of Fig. 1(a)-(b) with sidesway inhibited (i.e., D - D0 = 0), the following conclusions can be drawn:
1) The induced moments, lateral deflections and critical loads are not affected by the initial out-of-plumb D0 as indicated by Eqs. (1–7). This is true as long as D0/h is small (< 0.1).
2) As expected, the end moments, maximum moment along the span, and lateral deflections are highly affected by the degree of fixity at the end supports and the magnitude and shape of the initial imperfection along the member.
3) The results obtained using the proposed closed-form expressions listed in Table 1 (see Ref. [1]) and the FEM computer program ABAQUS are in excellent agreement.
Based on the results shown in Figs. 6-9 for columns of Fig. 1c-d with sidesway uninhibited and partially inhibited (i.e., D - D0 ≠ 0), the following conclusions can be drawn:
1) The induced moments, lateral deflections, and critical loads are affected by the initial out-of- plumb D0 as indicated by Eqs. (8)-(12).
]]> 2) Figs. 6(c) and 9(c) indicate that as the axial load increases in the columns of Figs. 1(c)-(d), the end moments Ma and Mb tend to become an equal magnitude and opposite (i.e., Ma = -Mb).3) The results obtained using the proposed closed-form expressions listed in Table 1 and the FEM computer program ABAQUS are in excellent agreement only up to the critical axial load; and
4) It was found that for D0/h = 0.002 and 0.10, the calculated values for Ma are slightly smaller than those from the FEM program ABAQUS using the proposed method with differences of about 0.05% and 2.8%, respectively. This indicates that the proposed closed-form expressions for columns with sidesway can be used with excellent accuracy as long as D0/h is small (<0.1), as stated previously.
Notice that: 1) all curves in Figs. 2(a)–5(a) and 8(a) and 9(a) have a point in common, indicating that the Figs. 3(a), 3(b) and 3(d) columns develop the same moment at end A when the applied axial load reaches P = Pe = p2EI/h2 for rotational fixities r > 0; 2) the curves in Figs. 2–9 can be used to directly calculate the end moment (Ma), the lateral deflection uh/2 or (D - D0), and the maximum moment (Mmax.) for the four column cases shown in Fig. 1, assuming that a = h/1000 (sinusoidal initial shapes) and out-of-plumbness D0 = h/500; and 3). Critical loads obtained using the proposed method can also be calculated with simplified expressions presented previously by Aristizabal-Ochoa (1994) (see Ref. [1]).
4. SUMMARY AND CONCLUSIONS
Several examples and closed-form solutions are presented which illustrate the effects of initial curvature, out-of-plumbness, and the end eccentricities on the induced bending moments, second-order deflections of slender prismatic columns with semirigid connections at both ends and with uninhibited, partially-inhibited, and totally-inhibited sidesway as the applied axial load is increased. The proposed closed-form solutions enable the analyst to explicitly evaluate these effects on their nonlinear elastic response and lateral stability. It is a common practice in the design of columns that the effects of initial geometric imperfections are taken into account for specific values according to accepted fabrication and erection tolerances. However, to investigate these effects when the magnitudes and shape of the imperfections are different from those adopted by the construction codes becomes a cumbersome task. Therefore, the proposed closed-form expressions might become a practical tool of great interest to structural designers and researchers to further the study of these effects in accordance with design practices and code specifications.
Analytical results and sensitivity studies indicate that the second-order response including the end reactions, bending moments, and deflections along a column are highly affected by the shape and magnitude of the initial imperfections, eccentricities of the applied axial load, the end fixities, and lateral bracing. Unlike a perfectly straight column, plumbed and loaded concentrically, which ideally remains straight up to its critical axial load, an imperfect column begins to bend as soon as the axial is applied with its end reactions, bending moments and deflections along a column, all increasing rapidly as the applied axial load increases, and consequently reaching inelastic strains at axial loads lower than that at the critical value of a perfect column. The larger the initial imperfections and the applied axial loads, the larger are the end reactions, bending moments, and deflections along a column. Thus columns with large initial imperfections, particularly those with a relatively large camber at midspan, can be expected to become unstable and fail at axial loads much below the critical load, while relatively straight and plumbed columns loaded concentrically will be able to support axial loads very close to their ideal critical load. In practice, the stability of columns is improved greatly by providing lateral support (bracing) against sidesway and large bending restraints against end rotations, and by reducing the initial imperfections, particularly the initial camber.
ACKNOWLEDGMENTS
]]> The research presented in this paper was carried out at the National University of Colombia, School of Mines at Medellin. The author wants to express his appreciation to DIME for the financial support, and Gabriel Colorado-Urrea and Hebert Arias-Cano undergraduate students and members of the Structural Stability Group of the National University of Colombia for running the verification using ABAQUS and preparing Figs. 2-9.
REFERENCES
[1] Aristizabal-Ochoa, J. D., Induced Moments and Lateral Deflections in Columns with Initial Imperfections and Semirigid Connections: i). Theory, Dyna, year 79, Nro. 172, pp. 7-17, 2012. [ Links ]
[2] Timoshenko, S. P., and Gere, J. M., Theory of Elastic Stability, 2nd Ed., McGraw-Hill Book Inc., New York, N.Y., pages 37, 59, 61 and 203, 1961. [ Links ] ]]>