
Lossless compression of hyperspectral images with pre-byte processing and intra-bands correlation
Lossless compresión de imágenes hiperespectrales con tratamiento pre-byte e intra-bandas de correspondencias
Assiya Sarinova a, Alexander Zamyatin b & Pedro Cabral c
a Department of University Management Informatization, S.Toraighyrov Pavlodar State University, Kazakhstan. assiya_prog@mail.ru
b Optimization and Control dept. Tomsk Polytechnic University, Geoinformatics and Remote Sensing lab. Tomsk State University, Russia alexander.zamyatin 1978@gmail.com
c Institute of Statistics and Information Management New University of Lisbon, Portugal, pcabral@isegi.unl.pt
]]> Received: May 27th, 2014. Received in revised form: July 23th, 2014. Accepted: July 23th, 2014.
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
Abstract
This paper considers an approach to the compression of hyperspectral remote sensing data by an original multistage algorithm to increase the compression ratio using auxiliary data processing with its byte representation as well as with its intra-bands correlation. A set of the experimental results for the proposed approach of effectiveness estimation and its comparison with the well-known universal and specialized compression algorithms is presented.
Keywords: remote sensing; hyperspectral images; lossless compression; intra-bands correlation; byte representation of data.
Resumen
Este documento se refiere a la compresión de datos hiperespectrales de teleobservación de la tierra mediante la sugerencia de un algoritmo de múltiples etapas para aumentar la relación de compresión, utilizando una formación de datos auxiliares de gran redundancia en su presentación de bytes y teniendo en cuenta la correlación intra-bandas. Aquí se presentan los resultados de los estudios sobre la eficacia de la compresión de imágenes hiperespectrales espaciales realizadas por el algoritmo de compresión propuesto con software de compresión universal y especializado.
Palabras clave: la teledetección; imágenes hiperespectrales, sin pérdida de compresión; intra-bandas de correlación; representación de bytes de datos.
]]> 1. Introduction
Modern centers for space monitoring and systems for remote sensing (RS) continually process, archive and distribute data, which constitute tens or hundreds of gigabytes [1-11]. A key problem in the process is compressing RS data to increase effectiveness of a data transfer via connection channels of limited carrying capacity and archiving in RS storage subsystems of a limited capacity. The necessary classification of this data must be of the highest value. That is why lossless compression which is free of any distortions of statistic brightness characteristics of restored data is more appropriate.
The solution of the compression problem, which is the most accessible for practical implementation presupposes the usage of universal and widely-known algorithms and means of compression, for instance, in the archival software WinRar, WinZip or compressor Lossless JPEG (JPEG-LS) on the base of JPEG [12-17] image compression standard. However, RS data is classified by various characteristics - spectral, radiometric, spatial resolutions and by geometrical size of the scene. The above-mentioned universal means of compression fail to consistently consider the variable differences [18-21]. Thus, there are multispectral and hyperspectral aerospace images (AI), which have essentially different parameters of spectral resolution and are characterized by high dependence (correlation) between data of different bands [22]. If for multispectral aerospace images the coefficient of mutual correlation of bands is R∈(0.3; 0.8), then for hyperspectral AI representing values of brightness which are received in various spectral bands with the high spectral resolution, the correlation of neighboring bands is R ≈ 1.0. This shows the high redundancy of data and the pertinence of applying this feature during compression [23,24].
Besides, knowing the correlation value (intra-bands correlation) between bands of hyperspectral AI, it is expedient to operate values of deviations (difference) between it and actual reference values, and that will allow the reduction of the range of data change and hence demand a smaller number of categories for their storage. The effective usage of specialized means of the compression is possible, considering the above-stated features of hyperspectral AI.
The software intended for the analysis of spatial data and processing of AI are ERDAS Imagine, ERDAS ER Mapper, ArcView GIS, GeoExpress and others often dispose of specific modules for compression of AI. Thus, the ERDAS Imagine package utilizes the compression tool for images in the MrSID format (IMAGINE MrSID Desktop Encoder and IMAGINE MrSID Workstation Encoder), based on wavelets and intended for lossy compression of large RS images. The ERDAS ER Mapper system has modules of loss compression on the basis of the standards JPEG2000 and ECW [25]. In the ArcView GIS package there is a MrSID module which compresses raster image files with loss [26]. The software product GeoExpress is intended for compressing raster data with the use of the popular formats MrSID and JPEG2000 [27]. Thus, all commercial systems of RS data processing have the means of loss compression on the basis of well-known standards.
Recent hyperspectral RS images lossless compression research attempts to apply various approaches and methods [28-33]. The separate stages of transforming data while compressing AI and the possibility of decreasing power inputs and algorithmic complexity are discussed. Additionally, there are various attempts at adapting standards, which have proven successful for compressing hyperspectral AI.
2. Description of the algorithm
Not all details of the original algorithms of compression are clear. Their numbers exceed the possibilities of most widespread means of compression when application to hyperspectral AI with various characteristics is uncertain.
It is our purpose to promote further search for approaches to lossless compression of hyperspectral RS images, substantially free from the disadvantages of existing universal and specialized facilities of compression.
]]> Considering the features of hyperspectral AI and some details of existing analogues, the most expedient solution of the problem of compressing hyperspectral AI is by multi-stage transformations: first the advantages of universal traditional approaches for data compression, and secondly to consider the specificity of hyperspectral data. The algorithm embodying this approach and some of its results are discussed below [31].Considering the specificity of compressing hyperspectral AI, the proposed algorithm has the following stages:
3. Compression of received data transformations with standard entropy algorithm by processing the generated auxiliary structures of the data.
Let us consider the details of the above-mentioned stages.
In the first stage, the value of deviations of the linear dependence on the matrix of values I[m,n,k].
For step-by-step description of the first stage consisting in searching correlation and deviations, it is necessary to take into account the following objects:
Step 1. To calculate a mathematical expectation mk of each band of the initial image I[m,n,k] and to place values to the file Q[k], as in (eq.1):
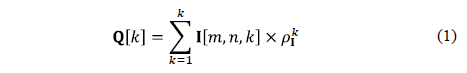
where 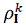 - relative frequency of occurrence of values of the image I, k=1,2,…, K.
- relative frequency of occurrence of values of the image I, k=1,2,…, K.
Step 2. To calculate (on the base of Q[k] and I[m,n,k]) correlation R for each pair of all available K bands of the initial image I[m,n,k], as in (eq.2):
]]>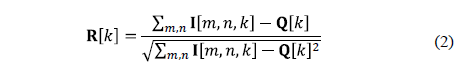
To place the result to R[k], k=1,2,…, K-1.
Step 3. To calculate (on the base of Q[k] and R[k]) a linear dependence of the kind L = mk × R for each pair of the available K bands of the initial image I[m,n,k]. Result should be placed to L[k], L[k] = Q[k] × R[k], k=1,2,…,K-1.
Step 4. To calculate (on the base of R[k] and L[k]) the difference between elements L[k] and corresponding values of the initial image I[m,n,k] in each of K bands, as in (eq.3):
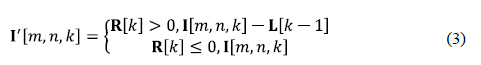
for m = 1..M, n = 1..N. The result is placed to I'[m,n,k].
Step 5. To transform the negative values I'[m,n,k] to positive ones in the byte representation as numbers with a sign demand more bytes than those without a sign (4):
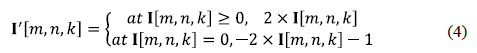
The result is the file I'[m,n,k] considering values of intra-bands correlation R[k].
The essence of the second stage consists of forming a file of unique pair groups of values that represent the initial image in the byte representation. Then, the file is formed containing references to the same pair group of values.
]]> The algorithm proceeds with two additional objects:The step-by-step elaboration for the second stage of transformation is shown in Fig.1:
Step 1. To form (on the base of I'[m,n,k]) a file M[j,k] for each band K adding unique pair groups of values in the byte representation from the file I'[m,n,k]. To place the result to M[j,k], j= 1,2,..,J. If repeated pair groups of values are absent, then J = (M×N×K)/2, k= 1,2,..,K.
Step 2. To form (on the base of M[j,k]) a file D[j,k], putting down references to unique pair groups of values from the file M[j,k] to D[j,k]. To place the result to D[j,k], j < J as j = M×N×K, k= 1,2,..,K.
At the end of the second stage, context modeling was used with the known arithmetic coding for compressing data of the file D[j,k] to the archival software D'[j,k].
In order to form an initial hyperspectral AI I[m,n,k] from D'[j,k] it is necessary to make a number of transformations opposed to the above-mentioned:
3. Experimental study
In order to access the effectiveness of the proposed algorithm in what concerns both the point compression ratio as the limits of its application, a number of experiments were performed using hyperspectral AI of the system RS AVIRIS (table 1) in data format of raster geoinformation system Idrisi Kilimanjaro. The AVIRIS (Airborne Visible/Infrared Imaging Spectrometer) system provides 224 spectral images with the wavelength of the band from 400 nanometers to 2500 nanometers. Also, the proposed algorithm was compared with the results of experiments received for universal archivers compression algorithms WinRar, WinZip and Lossles JPEG which applies the resolution of compression standard JPEG widely used in commercial compression systems.
The experiments were undertaken using a computer with the Intel Core i5 processor, 2,5 GigaHerz and RAM 4 Gigabit under operating system Windows 7 (updating package 3).
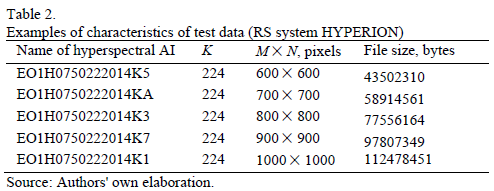
To estimate the robustness of the proposed algorithm another hyperspectral remote sensing (RS) data system HYPERION was also used (table 2). Hyperion hyperspectral sensor apparatus Earth Observing-1 is able to record 220 spectral images from 0.4 to 2.5 microns, with a spectral resolution of 0.1 to 0.11 micron.
]]>
A sequence of stages was then performed to find the most effective:
Sequence I - Consideration of correlation (1) forming auxiliary data with unique pair groups and references to them (2)
forming auxiliary data with unique pair groups and references to them (2) arithmetic coding (3).
arithmetic coding (3).
Sequence II - Forming auxiliary data with unique pair groups and references to them (1) 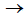 arithmetic coding (2).
arithmetic coding (2).
Sequence III - Consideration of correlation (1) 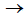 arithmetic coding (2).
arithmetic coding (2).
Sequence IV - Forming auxiliary data with unique pair groups and references to them (1) 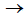 consideration the correlation (2)
consideration the correlation (2) 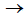 arithmetic coding (3).
arithmetic coding (3).
In order to evaluate the most productive sequence considering the contribution of each of these stages, a number of experiments with the different variants was conducted (Figure 2).
A fragment of the results of this experiment is displayed in Figure 2. This shows that various stages of the algorithm have different levels of importance while forming a result. In the 1st, 2nd and 4th variants of the stage sequences, the results surpass Losless JPEG indifferent degrees (from 25% to 46%).
The best result is achieved by sequence I with the highest compression ratio. The results of undertaking sequence II show that the absence of the stage of intra-bands correlation leads to an insignificant exponent of compression in comparison with Losless JPEG.
]]> Realization of the stages sequence in accordance with sequence III leads to the most insignificant result as there is no powerful formation of unique pair groups and references to them with creation of corresponding auxiliary structures of data.In Figure 3, the results of comparative experiments demonstrate the superiority of the proposed algorithm over analogues in exponent of compression Dcs at the varied geometrical sizes of RS hyperspectral data of AVIRIS (I) and HYPERION (II) systems. At increasing the geometrical size of the scenes, all the investigated algorithms show a steady result which exhibits little to no change.
Research was conducted to explore the dependence of compression exponent Dcs on the number of bands of AI K (Figure 4). Results show that compression exponent Dcs is increasing proportionally to the number of bands Kas and that the redundancy of the data of RS hyperspectral data of AVIRIS (I) and HYPERION (II) systems raises.
In conducting comparative research of compression exponents it is necessary to pay attention to calculating expenses of compression algorithms for AVIRIS (I) and HYPERION (II) RS systems (Figure 5).
As seen in Figure 5, in the proposed algorithm, the calculated effectiveness in comparison with analogues increased 3 fold. This is explained by an improved multi-stage algorithm which is provided to form auxiliary structures of data on AI considering the correlation and the following arithmetic coding.
Universal archival software does not take into account the specificity of the data being compressed and does not account for such operations.
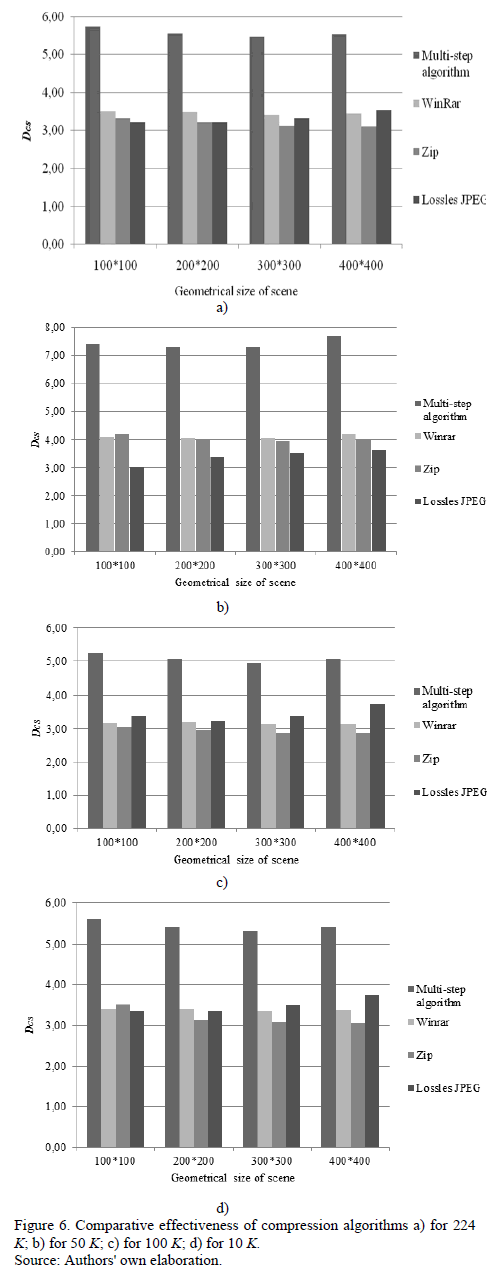
A large number of studies in different dimensions and number of bands were conducted. The compression ratios results are presented in Figure 6 (AVIRIS) and Figure 7 (HYPERION).
]]>
4. Conclusion
This work has been supported by the Russian Foundation for Basic Research (grant No 14-07-00027a).
]]> References
[1] Bondur, V., Modern approaches to processing of hyperspectral space images. Research Institute of space monitoring "Aerospace". Moscow, 2013, 4 P. [ Links ]
[2] Popov, M. and Stankevich, S., Optimization methods of spectral bands number in tasks of processing and data analysis of distance remote sensing of the earth. Scientific center of aerospace earth research, 1, pp. 106-112, 2003. [ Links ]
[3] Wang, H., Babacan, S. and Sayood, K., Lossless hyperspectral-image compression using context-based conditional average, 45 (12), pp. 4187-4193, 2007 [ Links ]
[4] Chengfu, H., Zhang, R. and Tianxiang, P., Lossless compression of hyperspectral images based on searching optimal multibands for prediction,6 (2), pp. 339-343, 2009. [ Links ]
[5] Liang, Y., Jianping, L. and Ke, G., Lossless compression of hyperspectral images using hybrid context prediction, 20 (7), pp. 199-206, 2012, [ Links ]
]]>[6] Aiazzi, B, Alparone, L., Baronti, S., Lastri, C. and Selva, M., Spectral distortion in lossy compression of hyperspectral data. Journal of Electrical and Computer Engineering, (2012), 8 P, 2012. DOI: 10.1155/2012/850637 [ Links ]
[7] Cheng-Chen, L. and Yin-Tsung, H., Lossless compression of hyperspectral images using adaptive prediction and backward search schemes. Journal of Information Science and Engineering, (27), pp. 419-435, 2011. [ Links ]
[8] Aiazzi, B., Alparone, L. and Baronti S., Near-lossless image compression by relaxation-labeled prediction. Signal Process, 82 (11), pp. 1619-1631, 2002. [ Links ]
[9] Magli, E., Olmo, G. and Quacchio, E., Optimized onboard lossless and near-lossless compression of hyperspectral data using CALIC. IEEE Geoscience and remote sensing letters, 1 (1), pp. 21-25, 2004. [ Links ]
[10] Zamyatin, A. and Cabral P., Markov processes in modeling land use and land cover changes in sintra-cascais, Portugal. DYNA, 76 (158), pp. 191-198, 2009. [ Links ]
[11] Zamyatin, A. and Cabral P., Advanced spatial metrics analysis in cellular automata land use and cover change modelingdyna. DYNA, 78 (170), pp. 42-50., 2011. [ Links ]
[12] Aiazzi, B., Baronti, S. and Alparone, L., Lossless compression of hyperspectral images using multiband lookup tables. IEEE Signal Process. Letters, 6 (16), pp. 481-484, 2009. [ Links ]
[13] Penna, B., Tillo, T., Magli, E. and Olmo, G., Transform coding techniques for lossy hyperspectral data compression. IEEE Geoscience and remote sensing letters, 45 (5), pp.1408-1420, 2007. [ Links ]
[14] RarLab. WinRar software system for compress files. [on line] [Date of reference: May 22th of 2014]. Available at: http://www.win-rar.com/rarproducts.html [ Links ]
[15] WinZip. Program of compression for Windows [on line] [Date of reference: May 22th of 2014]. Available at: http://www.winzip. com/ru/prodpagewz.htm [ Links ]
[16] Tang, X., Pearlman, W. and Modestino, J., Hyperspectral image compression using three-dimensional wavelet coding. Proc. SPIE IS&T, (1), pp. 1037-1047, 2003. [ Links ]
[17] Penna, B., Tillo, T., Magli, E. and Olmo, G., Progressive 3-D coding of hyperspectral images based on JPEG 2000. IEEE Geoscience and remote sensing letters,1 (3), pp. 125-129, 2006. http://dx.doi.org/10.1109/LGRS.2005.859942 [ Links ]
[18] Zhang, J. and Liu, G., An efficient reordering prediction-based lossless compression algorithm for hyperspectral images. IEEE Geoscience and remote sensing letters, 2 (4), pp. 283-287, 2007. http://dx.doi.org/10.1109/LGRS.2007.890546 [ Links ]
[19] Mielikainen, J., Kaarna, A. and Toivanen, P., Lossless hyperspectral image compression via linear prediction. Proc. SPIE 4725, (8), pp. 600-608, 2002. http://dx.doi.org/10.1117/12.478794 [ Links ]
[20] Rizzo, F., Carpentieri, B., Motta, G. and Storer, J., A. Low-complexity lossless compression of hyperspectral imagery via linear prediction. IEEE Signal Process. Lett, 2 (12), pp. 138-141, 2005. http://dx.doi.org/10.1109/LSP.2004.840907 [ Links ]
[21] ISO/IEC 15444-1. JPEG2000 Image Coding System [on line] [Date of reference: May 22th of 2014]. Available at: http:/www.jpeg.org/public/15444-1annexi.pdf [ Links ]
[22] Kiely, A., Klimesh, M., Xie, H. and Aranki, N., Icer-3D: A progressive wavelet-based compressor for hyperspectral images, JPL IPN Progress Report, 42 (164), 2006. [ Links ]
[23] Gueguen, L., Trocan M., Pesquet-Popescu B., Giros, A. and Datcu, M., A comparison of multispectral satellite sequence compression approaches. Signals, Circuits and Systems, 1, pp. 87-90, 2005. [ Links ]
[24] Zamyatin, A. and Chung T.D., Compression of multispectral space images using wavelet transform and intra-bands correlation. Journal of Tomsk Polytechnic University, 313 (5), pp. 20-24, 2008. [ Links ]
]]>[25] Interregional public organization promoting the market development of geographic information technologies and services "GIS-Association", [on line] [Date of reference: May 22th of 2014]. Available at: http://www.gisa.ru/1489.html [ Links ]
[26] Arc View GIS [on line] [Date of reference: May 22th of 2014]. Available at: http://gisa.ru/3577.html [ Links ]
[27] Geo-information systems [on line] [Date of reference: May 22th of 2014]. Available at: http://loi.sscc.ru/gis/default.aspx [ Links ]
[28] Vatolin, D., Ratushnyak, A., Smirnov, M. and Yukin, V., Data compression methods. M.: Dialog-MIFI, 2003, 384P. [ Links ]
[29] Kopylov, V., Creation basics of aerospace environment monitoring. Yekaterinburg: PP "Kontur", 2006 P. [ Links ],
[30] Modern and perspective developments and technologies in a space instrumentation. Compression of multispectral images with out loss or limited losses. Moskva, IKI RAN, (1), 2004. [ Links ]
[31] Rizzo, F., Carpentieri, B. Motta, G. and Storer, J., Low-complexity lossless compression of hyperspectral imagery via linear prediction. IEEE Signal Process. Letters, 2 (12), pp. 138-141, 2005. http://dx.doi.org/10.1109/LSP.2004.840907 [ Links ]
[32] Motta, G., Rizzo, F. and Storer, J., Hyperspectral data compression. Berlin: Springer, 2006. http://dx.doi.org/10.1007/0-387-28600-4 [ Links ]
[33] Zamyatin, A., Sarinova, A. and Cabral, P., The compression algorithm of hyperspectral space images using pre-byte processing and intra-bands correlation. GEOProcessing 2014. The Sixth International Conference on Advanced Geographic Information Systems, Applications, and Services, pp.70-75, 2014 [ Links ]
A. Sarinova, completed a BSc. Eng in Computer Systems for Information Processing and Management in 2009, and a MSc in Information Science in 2011. Graduate student in the area processing of aerospace images, Faculty of Informatics, Tomsk State University, Russia. She is Senior Lecturer (Dept."MIT", InEU) and a software engineer in the Dept. Informatization, in S.Toraighyrov Pavlodar State University, Kazakhstan.
A. Zamyatin, received a BSc Eng and MSc Eng in Automatics and Computers in 1999 and 2001, PhD in 2005 and Habilitation in 2012. He has 10+ years' experience in advanced remote sensing data processing - supervised and unsupervised multidimensional classification, parametric and non-parametric statistics, artificial neural networks, texture analysis, Markov chains, stochastic spatial modeling, time series analysis, models validation, loss and lossless data compression, high-performance computation, experimental design using existing and innovative algorithms and software. He is currently working at Tomsk Polytechnic University in the Optimization and Control dept. and in Tomsk State University in Geoinformatics and Remote Sensing lab, Russia.
P. Cabral, graduated in Statistics and Information Management in 1997, in the ISEGI-NOVA, Portugal; earned a MSc in Geographical Information Systems in 2001, in the IST-UTL, Portugal and a PhD in Mathematics and Applications to Social Sciences in 2006, in the EHESS, France. He is Assistant Professor at ISEGI-NOVA in the area of GIS.
]]>