
A relax and cut approach using the multi-commodity flow formulation for the traveling salesman problem
Un enfoque relax and cut usando una formulación de flujo multiproductos para el problema del agente viajero
Makswell Seyiti Kawashima a, Socorro Rangel b, Igor Litvinchev c & Luis Infante d
a UNESP - Univ Estadual Paulista, São José do Rio Preto, SP, Brazil, maksmx@gmail.com,
b UNESP - Univ Estadual Paulista, São José do Rio Preto, SP, Brazil, socorro@ibilce.unesp.br
c UANL-Universidad Autónoma de Nuevo León. San Nicolás de los Garza, NL, México, igorlitvinchev@gmail.com
d UANL-Universidad Autónoma de Nuevo León. San Nicolás de los Garza, NL, México luisinfanterivera@gmail.com
Received: January 28th, 2015. Received in revised form: March 26th, 2015. Accepted: April 30th, 2015.
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.

Abstract
In this paper we explore the multi-commodity flow formulation for the Asymmetric Traveling Salesman Problem (ATSP) to obtain dual bounds. The procedure employed is a variant of a relax and cut procedure proposed in the literature that computes the Lagrangean multipliers associated to the subtour elimination constraints preserving the optimality of the multipliers associated to the assignment constraints. The results obtained by the computational study are encouraging and show that the proposed algorithm generated good dual bounds for the ATSP with a low execution time.
Keywords: traveling salesman problem; relax and cut; Lagrangean relaxation.
Resumen
En este artículo nosotros exploramos una formulación de flujo multiproductos para el Problema del Agente Viajero Asimétrico (ATSP) en la obtención de cotas duales de este problema. El procedimiento empleado es una variante del método relax and cut propuesto en la literatura que computa los multiplicadores lagrangianos asociados a las restricciones de eliminación de subrutas preservando la optimalidad de los multiplicadores asociados a las restricciones de asignación. Los resultados obtenidos con la experimentación computacional son alentadores y muestran que el algoritmo propuesto genera buenas cotas duales con un tiempo de ejecución bajo.
Keywords: problema del agente viajero; relax and cut; relajación lagrangiana.
1. Introduction
The Traveling Salesman Problem (TSP) has been the subject of many works beginning with the seminal paper of Dantzig, Fulkerson, and Johnson in 1954 [3]. The applications can vary from everyday routing problems e.g. [1,17], to production planning problems [13]. Many of these works also discuss models and solution approaches for the TSP. For the majority of solution approaches, it is important to have good primal and dual bounds. The latter can be obtained by exploring different types of relaxations.
The linear relaxation of a Mixed Integer formulation to an optimization problem can provide a dual bound and its quality depends on how close the formulation is to the convex hull of solutions.  ncan et al. [14] review several mathematical formulations for the ATSP and discuss the quality of the associated bounds. The difference among the formulations is how the subtour elimination constraints are formulated. The formulation presented in [3], known as DFJ, provides a stronger dual bound and has been the basis for several solution methods for the ATSP [e.g. 16]. However it has an exponential number of subtour elimination constraints. Another formulation is the multi-commodity flow formulation (MC-ATSP) and it uses a polynomial number of constraints to eliminate subtours. It is as strong as the DFJ formulation; however, it might present difficulties when it comes to solving the associated linear relaxation.
ncan et al. [14] review several mathematical formulations for the ATSP and discuss the quality of the associated bounds. The difference among the formulations is how the subtour elimination constraints are formulated. The formulation presented in [3], known as DFJ, provides a stronger dual bound and has been the basis for several solution methods for the ATSP [e.g. 16]. However it has an exponential number of subtour elimination constraints. Another formulation is the multi-commodity flow formulation (MC-ATSP) and it uses a polynomial number of constraints to eliminate subtours. It is as strong as the DFJ formulation; however, it might present difficulties when it comes to solving the associated linear relaxation.
Due to the computational effort necessary to solve the linear relaxation of the MC-ATSP, Rocha, Fernandes, and Soares [16] apply a Lagrangean relaxation to derive dual bounds for the ATSP. In the present paper, we also explore Lagrangean bounds for the MC-ATSP formulation. However, instead of dualizing all the subtour elimination constraints at once, we dualize only the ones that are violated by the current solution of the relaxed problem. This idea has been denominated the Relax and Cut procedure. It was introduced in the works of Balas and Christofides [2] and Gavish [7], and it has been the subject of many studies in recent years, although it has not always been referred to as such [2,4,-6,8,9, 16,18].
To briefly describe the relax and cut method, consider an integer optimization problem (IP) defined by (1)-(4).
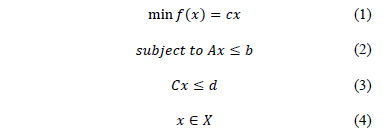
A relaxation of (IP) can be obtained by removing the constraints (2), and is denominated (RP). Let 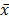 be the optimal solution of (RP), and let
be the optimal solution of (RP), and let 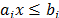 be a constraint of (IP) that is violated by
be a constraint of (IP) that is violated by 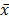 . A Lagrangean type relaxation of problem (IP) can be built by dualizing the violated constraint using
. A Lagrangean type relaxation of problem (IP) can be built by dualizing the violated constraint using 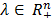 as stated in problem (LRP) defined by (5)-(7).
as stated in problem (LRP) defined by (5)-(7).
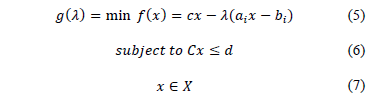
Fixing the value of 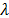 it is possible to obtain a dual bound for problem (IP). The best bound that can be obtained by the relaxation (LRP) is found by solving the associated dual problem stated in (8).
it is possible to obtain a dual bound for problem (IP). The best bound that can be obtained by the relaxation (LRP) is found by solving the associated dual problem stated in (8).
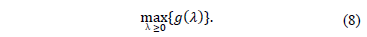
Having solved the problem (8), it might be possible to improve the dual bound obtained so far by identifying new valid inequalities for (IP) that are not satisfied by the current solution of (8), reformulating the relaxation (LRP) by dualizing them in a Lagrangean fashion, and solving the new Lagrangean dual problem. This procedure has been coined by Lucena [11] as a Delayed Relax and Cut method. A different procedure, coined as Non-Delayed Relax and Cut in [12], identifies new violated valid inequalities and reformulates the relaxation each time a multiplier is updated.
The remainder of this paper is organized as follows. The non-delayed relax and cut method applied to a generic formulation of the ATSP is presented in section 2. In Section 2.1, the procedure presented in [2] for the DFJ formulation is briefly described followed by the description of our proposal to adapt it for MC-ATSP formulation presented in Section 2.2. A numerical study comparing the two procedures is presented in Section 3 and concluding remarks are given in Section 4. This paper is an extension of work presented at the CILOG 2014 [10].
2. The non-delayed relax and cut method applied to the ATSP
Consider a Graph 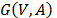 with
with 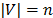 ,
, 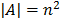 and a cost
and a cost 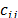 for each arc
for each arc 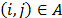 . A generic mathematical formulation for the ATSP problem is stated in (9)-(13) and is denominated (GATSP).
. A generic mathematical formulation for the ATSP problem is stated in (9)-(13) and is denominated (GATSP).
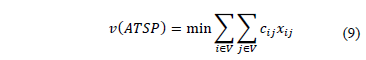
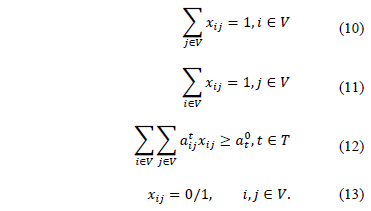
The variable 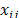 defines whether city
defines whether city 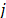 succeeds city
succeeds city 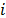 in the Hamiltonian cycle. The objective function (9) states the search for the minimum cost Hamiltonian cycle. Constraints (10)-(11) guarantees that each city is included exactly once in the Hamiltonian cycle. The constraints set (12) state the usual subtour elimination constraints in a generic format [2].
in the Hamiltonian cycle. The objective function (9) states the search for the minimum cost Hamiltonian cycle. Constraints (10)-(11) guarantees that each city is included exactly once in the Hamiltonian cycle. The constraints set (12) state the usual subtour elimination constraints in a generic format [2].
If constraints (12) are dropped we obtain a relaxation for the ATSP and this problem is known as the Assignment Problem (AP). Given the properties of the constraint matrix of (AP), it can be solved as a continuous linear optimization problem. Let 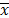 be the optimal primal solution to the continuous version of (AP),
be the optimal primal solution to the continuous version of (AP), 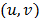 be the associated optimal dual solution and
be the associated optimal dual solution and 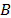 be the associated optimal basis. If
be the associated optimal basis. If 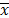 is feasible to the GATSP, we are done. Otherwise, it is of interest to compute strong primal and dual bound for the GATSP. In what follows, the non-delayed relax and cut method will be applied to the GATSP formulation in order to obtain dual bounds.
is feasible to the GATSP, we are done. Otherwise, it is of interest to compute strong primal and dual bound for the GATSP. In what follows, the non-delayed relax and cut method will be applied to the GATSP formulation in order to obtain dual bounds.
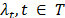 , be the Lagrangean multipliers associated to constraints (12) and
, be the Lagrangean multipliers associated to constraints (12) and 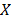 be the feasible set associated to the relaxation (AP). Dualizing the constraints (12) we get the Lagrangean function (14).
be the feasible set associated to the relaxation (AP). Dualizing the constraints (12) we get the Lagrangean function (14). 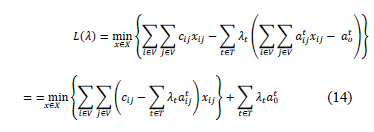
A dual bound (DL) for the ATSP can be obtained by solving the associated Lagrangean dual (15).
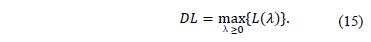
Several methods can be used to solve (15), among them the subgradient method and the Volume algorithm (e.g. [8], [16]). Balas and Christofides [2] propose a non-delayed relax and cut algorithm in which the search for the optimal Lagrangean multipliers is done by searching for l values that maintains the optimality of the primal solution 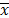 for the relaxation (AP). That is, the search for
for the relaxation (AP). That is, the search for 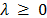 that improve the dual bound given by the relaxation (AP),
that improve the dual bound given by the relaxation (AP), 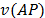 , is limited to dual solutions such that conditions (16) and (17) are satisfied.
, is limited to dual solutions such that conditions (16) and (17) are satisfied.
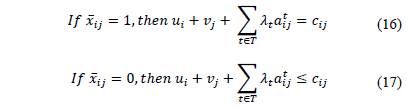
That is, conditions (16) and (17) impose the search for 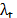 among the values that guarantee feasible solutions to the dual of the problem (AP), problem (DAP) defined by (18)-(20)
among the values that guarantee feasible solutions to the dual of the problem (AP), problem (DAP) defined by (18)-(20)
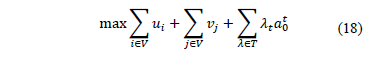
Subject to
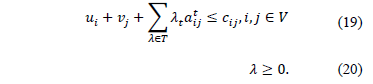
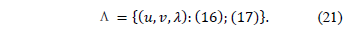
The Lagrangean dual problem (15) can be restated as (22).
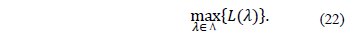
Note 1. We say that a constraint admits a positive multiplier if there is 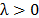 such that
such that 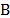 is optimal to (AP) and when it is dualized in a Lagrangean fashion it gives a better dual bound.
is optimal to (AP) and when it is dualized in a Lagrangean fashion it gives a better dual bound.
Proposition 1. [2] If only a subset 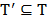 of constraints (12) are used to build the Lagrangean function L(l), then:
of constraints (12) are used to build the Lagrangean function L(l), then:
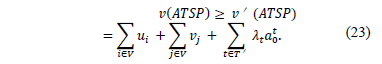
The procedure proposed in [2] attempts to improve the dual bounds to the (ATSP) iteratively while keeping the solutions 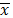 and
and 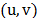 , respectively, primal and dual optimal for (AP). The procedure identifies valid inequalities that:
, respectively, primal and dual optimal for (AP). The procedure identifies valid inequalities that:
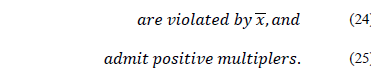
Once valid inequalities that satisfy (24) and (25) are identified, they are included in the (AP) formulation and dualized in a Lagrangean fashion with the maximum possible value that satisfies (16) and (17). The addition of new constraints to the reformulated (AP) implies in addition of new variables to the dual problem (18)-(20), in the term 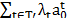 of (23), so improving the dual bound given by the partial Lagrangean function
of (23), so improving the dual bound given by the partial Lagrangean function 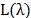 . Given that violated constraints are identified (cut) and used to build a new Lagrangean relaxation to the problem it is a relax and cut procedure. Moreover, since the cuts are identified each time a new Lagrangean solution is found, the procedure proposed in [2] can be called a non-delayed relax and cut procedure, or simply RCP. In what follows, we will specify how to obtain valid inequalities that satisfy (24) and (25).
. Given that violated constraints are identified (cut) and used to build a new Lagrangean relaxation to the problem it is a relax and cut procedure. Moreover, since the cuts are identified each time a new Lagrangean solution is found, the procedure proposed in [2] can be called a non-delayed relax and cut procedure, or simply RCP. In what follows, we will specify how to obtain valid inequalities that satisfy (24) and (25).
Balas and Christofides [2] develop the RCP procedure for three types of subtour elimination constraints (cut set, clique and articulation point). To identify violated inequalities that admit positive multipliers, they consider an auxiliary spanning graph 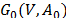 in which there is an arc in
in which there is an arc in 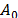 for each variable with zero reduced cost (i.e.an arc for each variable that satisfies (19) at equality).
for each variable with zero reduced cost (i.e.an arc for each variable that satisfies (19) at equality).
In the case of the cut set constraints, if 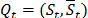 is the cut set associated to
is the cut set associated to 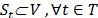 . Then the cut constraint (26) admits a positive multiplier if and only if condition (27) is satisfied.
. Then the cut constraint (26) admits a positive multiplier if and only if condition (27) is satisfied.
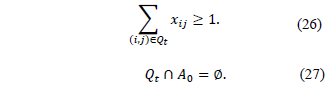
More details of how to identify violated cut set constraints can be found in [2] and [10].
2.2. The Relax and Cut procedure for the ATSP multi-commodity formulation
A strong formulation for the ATSP, with a polynomial number of constraints, is based on the multi-commodity network flow problem (e.g. [14]). In this formulation, the subtour elimination constraints are formulated in terms of a flow of 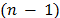 commodities in a network. The reasoning is based on the assumption that there are
commodities in a network. The reasoning is based on the assumption that there are 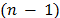 commodities available at city 1 and a demand of one unit of commodity
commodities available at city 1 and a demand of one unit of commodity 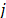 ,
, 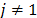 at city
at city 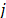 . The formulation is an extended one in the sense that besides the binary assignment variables
. The formulation is an extended one in the sense that besides the binary assignment variables 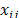 , a set of continuous variables
, a set of continuous variables 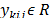 are defined to represent the flow of a commodity
are defined to represent the flow of a commodity 
through the arc  . The multi-commodity subtour elimination constraints are defined by (28)-(31).
. The multi-commodity subtour elimination constraints are defined by (28)-(31).
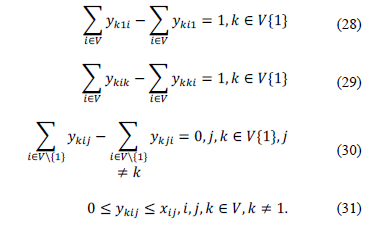
The constraints (28) guarantee that there is one unit of commodity 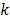 available at node 1 and this product cannot flow back to node 1. For each node
available at node 1 and this product cannot flow back to node 1. For each node 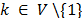 , constraint (29) imposes that the demand for product
, constraint (29) imposes that the demand for product 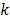 in node
in node 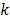 is met. Constraints (30) are the flow conservation constraints. Finally, constraints (31), impose that the flow of product
is met. Constraints (30) are the flow conservation constraints. Finally, constraints (31), impose that the flow of product 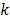 goes through arc
goes through arc 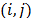 only if this arc is included in a path from node 1 to node
only if this arc is included in a path from node 1 to node 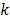 . The multi-commodity formulation for the ATSP, MC-ATSP, is given by (9)-(11), (13) and (28)-(31). In what follows, we detail the RCP procedure defined in Section 2 to obtain dual bounds for the ATSP considering the MC-ATSP formulation.
. The multi-commodity formulation for the ATSP, MC-ATSP, is given by (9)-(11), (13) and (28)-(31). In what follows, we detail the RCP procedure defined in Section 2 to obtain dual bounds for the ATSP considering the MC-ATSP formulation.
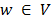 that is not in the same subtour that includes node 1, denoted hereafter as
that is not in the same subtour that includes node 1, denoted hereafter as 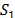 . That is, condition (24) is satisfied for every
. That is, condition (24) is satisfied for every  . Let us now derive the conditions to identify among the violated constraints the ones that admit positive multipliers.
. Let us now derive the conditions to identify among the violated constraints the ones that admit positive multipliers. In order to do that, let us build the dual problem associated to the linear relaxation of MC-ATSP. For each commodity 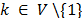 , define
, define 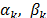 and
and 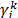 as the dual variable associated to (28), (29) and (30) respectively. For each node
as the dual variable associated to (28), (29) and (30) respectively. For each node 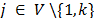 ,
, 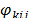 is the dual variable associated to (31). Let
is the dual variable associated to (31). Let 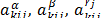 and
and 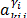 be the nonzero coefficients of the flow variable
be the nonzero coefficients of the flow variable 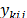 in constraints (28), (29), (30) and (31) respectively. A column of the constraints' matrix of the MC-ATSP associated to the
in constraints (28), (29), (30) and (31) respectively. A column of the constraints' matrix of the MC-ATSP associated to the 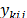 variable is represented in Fig. 1, in which the coefficients are defined according to (32)-(35).
variable is represented in Fig. 1, in which the coefficients are defined according to (32)-(35).
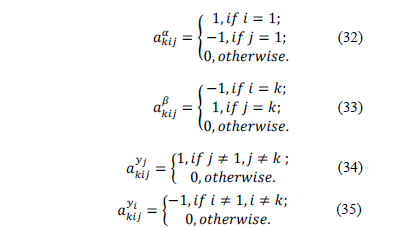
The dual problem associated to the MC-ATSP formulation is defined by (36)-(39).
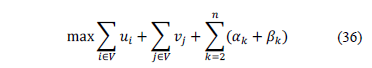
Subject to
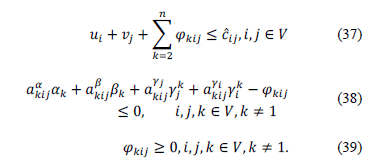
The main idea of the RCP is to dualize only the multi-commodity constraints that have a positive multiplier and therefore guarantee an improvement in the quality of the Lagrangean dual bound. As we can see in the objective function (36), to obtain better bounds it is necessary to identify constraints such that condition (40) is met, in which 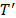 is the set of dualized constraints.
is the set of dualized constraints.
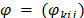 , associated to (27), has sign constraints. Therefore to guarantee (39), let
, associated to (27), has sign constraints. Therefore to guarantee (39), let 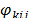 be fixed to the current value of the reduced cost,
be fixed to the current value of the reduced cost, 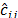 , associated to the primal variable
, associated to the primal variable 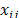 , see expression (41).
, see expression (41). 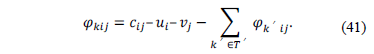
To simplify the notation, fixing 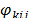 to the value defined in (41), constraints (37) and (38) can be replaced by (42) in the dual problem.
to the value defined in (41), constraints (37) and (38) can be replaced by (42) in the dual problem.
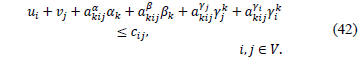
Now, it is necessary to derive feasible values to the dual variables 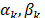 and
and 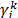 , for
, for 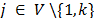 . There are two cases. In the first case, we consider
. There are two cases. In the first case, we consider 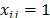 . To simplify the exposition, suppose that no subtour elimination constraints have been dualized yet,
. To simplify the exposition, suppose that no subtour elimination constraints have been dualized yet, 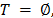 and take a subtour
and take a subtour 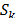 that contains node
that contains node 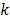 . Let
. Let 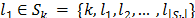 such that
such that 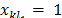 . Then the dual constraint associated to the variable
. Then the dual constraint associated to the variable 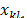 (42) is:
(42) is:
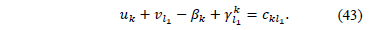
The associated slack variable is zero and so for 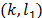 ,
, 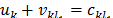 and we obtain (44) and (45).
and we obtain (44) and (45).
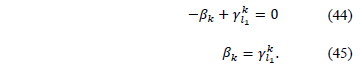
Consider now a second node 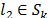 such that
such that 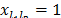 , similarly we have:
, similarly we have:
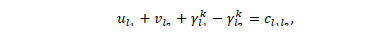
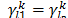 . Continuing this reasoning we have:
. Continuing this reasoning we have: 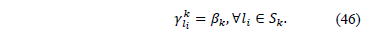
Consider now a node in the same subtour as node 1, 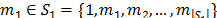 such that
such that 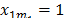 . According to (42):
. According to (42):
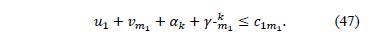
As the associated slack, reduced cost, is zero (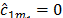 ) we get the equality
) we get the equality 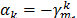 , which is also valid for the other nodes
, which is also valid for the other nodes 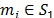 , that is:
, that is:
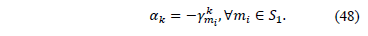
And so, 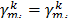 for
for 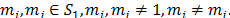 In general, for a subtour
In general, for a subtour 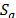 ,
, 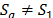 and
and 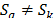 , and any distinct nodes
, and any distinct nodes 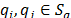 we have (50).
we have (50).

Consider now the case when 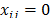 . Let
. Let 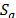 and
and 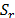 be two distinct subtours and the nodes
be two distinct subtours and the nodes 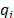 and
and 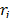 , both different from 1 and
, both different from 1 and 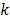 . Consider also the arc
. Consider also the arc 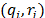 and the respective constraint (42):
and the respective constraint (42):
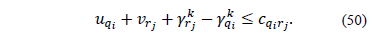
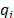 and
and 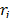 do not belong to the same subtour, then
do not belong to the same subtour, then 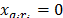 . Moreover, as
. Moreover, as 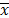 is the optimal solution to (AP), it is possible to say that
is the optimal solution to (AP), it is possible to say that 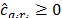 , that is,
, that is,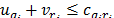 . As
. As 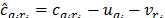 , to keep the dual feasibility and according to (51):
, to keep the dual feasibility and according to (51): 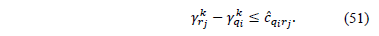
Since (51) and picking one node in each subtour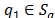 and
and 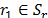 we have:
we have:
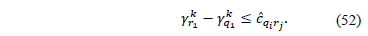
The inequality (53) is valid for any 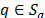 and
and 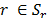 . Then:
. Then:
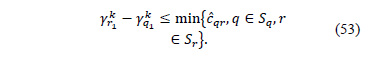
Similarly, taking the arc 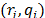 we have:
we have:
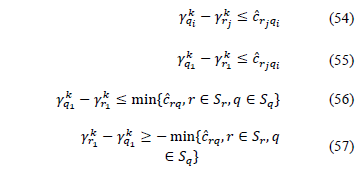
We can restate (58) as,
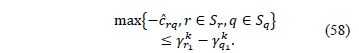
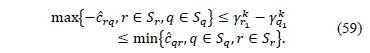
To obtain (60), we supposed that 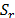 and
and 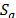 were different from both
were different from both 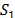 and
and 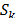 . Using a similar argument and considering node
. Using a similar argument and considering node 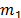 as representing the subtour
as representing the subtour 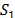 we get
we get 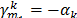 , and for
, and for 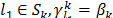 . Then we can derive:
. Then we can derive:
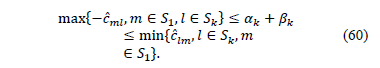
which gives bounds to 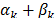 that keeps the dual feasibility of the optimal basis
that keeps the dual feasibility of the optimal basis 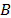 . If
. If 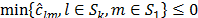 then the constraints associated to
then the constraints associated to 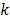 do not admit positive multipliers. Otherwise, the maximum possible values for
do not admit positive multipliers. Otherwise, the maximum possible values for 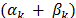 can led to an improved dual bound.
can led to an improved dual bound.
To summarize the optimization problem associated to the definition of the best values for 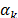 and
and  , let:
, let:
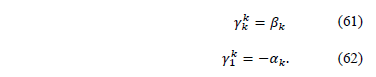
From (47) and (62) we have that:
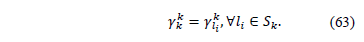
Similarly, from (49) and (63) we get:
]]>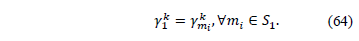
The problem to identify violated multi-commodity inequalities with positive multipliers is given by (66)-(70).

Subject to
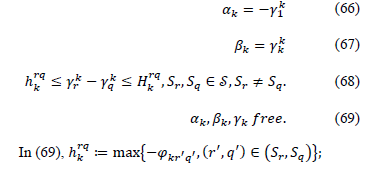
In (69), 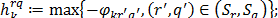
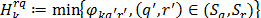 ;
; 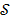 is a collection of subtours associated to
is a collection of subtours associated to 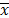 ;
; 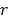 and
and 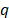 are nodes in
are nodes in 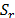 and
and 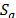 , respectively,with
, respectively,with 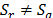 .
.
If the optimal solution 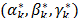 of (66)-(70) is greater than zero, the set of constraints (28)-(31) associated to
of (66)-(70) is greater than zero, the set of constraints (28)-(31) associated to 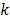 is violated by
is violated by 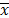 and dualized with positive multipliers. The reduced costs can be updated according to (71).
and dualized with positive multipliers. The reduced costs can be updated according to (71).
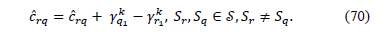
The MC-RCP procedure consists in iteratively evaluating all the subtours through the nodes 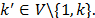 According to (36), at the end of the procedure an improved dual bound (
According to (36), at the end of the procedure an improved dual bound (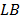 ) for the ATSP is given by (72).
) for the ATSP is given by (72).
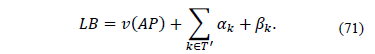
The pseudocode of the MC-RCP procedure is shown in Fig. 2.
3. Computational Study
In this section, we present results of the computational implementation of the procedure relax and cut considering the cut set constraints (Procedure CS-RCP described in Section 2.1) and the multi-commodity constraints (Procedure MC-RCP described in Section 2.2). The multi-commodity
formulation for the ATSP, model MC-ATSP, was written in the syntax of the AMPL modeling language. The CS-RCP and the MC-RCP algorithms were coded in the C++ programming language, using the CPLEX 12.5 libraries and run on a machine with Intel Core i5 2.67 GHz with 3.80 GB of RAM, operating system Windows 7 Ultimate. A maximum of 30 minutes (1800 seconds) of CPU time was allowed in each run. Thirteen instances of the TSPLIB library [15] were used in the tests (br17, ftv33, ftv35, ftv38, p43, ftv44, ftv47, ft53, ftv55, ftv64, ft70, ftv70, ftv170) ranging from 17 to 171 nodes. The instances size and the corresponding optimal solution values are given in [15].
As described in section 2, the relax and cut algorithms start from a solution of the Assignment Problem (AP) and search for violated valid inequalities that admits positive multipliers. For the cut set subtour elimination constraints (procedure CS-RCP), identifying valid inequalities is related to the existence of a reachable set 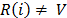 of a node
of a node 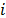 in the admissible graph
in the admissible graph 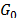 [10]. As for the multi-commodity subtour elimination constraints (procedure MC-RCP) the search is undertaken through all the subtours that do not include node 1 (see Fig. 2).
[10]. As for the multi-commodity subtour elimination constraints (procedure MC-RCP) the search is undertaken through all the subtours that do not include node 1 (see Fig. 2).
At first the instances of the AP and the MC-ATSP models, as well as the linear relaxation of the model MC-ATSP (RMC-ATSP) were solved by the solver CPLEX using the default parameters, except for the instances of the relaxation RMC-ATSP that were solved by the barrier method, as suggested in [14]. It was not possible to find feasible solution for 6 instances (p43, ftv44, ftv55, ft70, ftv70 and ftv170) of the model MC-ATSP in 30 minutes (the allowed execution time). Also, the solver runs out of memory when solving instance ftv170 of the MC-ATSP model. The linear relaxation of the multi-commodity formulation is indeed very strong, it provided an average gap of 1.03%. The gap associated to the relaxation AP of the instances br17 and p43 is very high, 100% and 97% respectively, which influences the results of the algorithms relax and cut as will be discussed next.
To compare two bounds 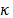 and
and 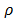 we compute their relative value
we compute their relative value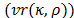 as in (73).
as in (73).
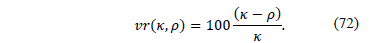
Table 1 presents comparisons between the RMC-ATSP relaxation (RMC) and the MC-RCP procedure (MC), presenting the obtained dual bounds, computational time, in seconds, and the relative value of the RMC and MC dual bounds, for each instance.
For most instances (9 out of 13) the MC-RCP procedure provided dual bounds with relative value of less than 10% of the bound given by the linear relaxation of the MC-ATSP model. For all but one instance, the average CPU time taken to solve the linear relaxation RMC-ATSP was 258.71 seconds while the average time to run the MC-RCP procedure was 4.96 seconds. The linear relaxation of the ftv170 instance of model MC-ATSP could not be solved in the allowed execution time for the solver (1800 seconds). Taken the optimal value for the instance ftv170 given in the TSPLIB, the MC-RCP provided a dual bound with a gap of 4.39% in 16.53 seconds.
We also compared the bounds given by the two relax and cut procedures presented in this work. Table 2 shows, for each instance, the dual bounds associated to the procedures CS-RCP and MC-RCP, CS and MC, respectively, and the corresponding CPU time (in seconds). For each bound (CS and MC), we also show the number of violated inequalities that are dualized in each procedure (cut), the integer gap and their relative value 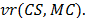
The CS-RCP and MC-RCP procedures gave similar results. In 10 out of the 13 instances, the relative value of the associated bounds was no greater than 3%. However, the particularities of some instances resulted in big differences in the results of the two procedures. For the instance, br17 v(AP) = 0, and the bound given by the MC-RCP procedure reduced the AP gap from 100% to 64.10%, whereas the CS-RCP procedure reduced it to 5.13%. The number of valid inequalities that can be identified in the CS-RCP procedure is higher than for the MC-RCP procedure. However, the proportion of cuts generated in relation to possible total is very close in both algorithms. The CS-RCP procedure identified 11 cuts out of 20, a ratio of 0.55, while the MC-RCP identified 3 out of 5, with a ratio of 0.6. It is noteworthy that for the instance ftv170 the dual bound and the number of cuts was the same in both procedures.
The work of Rocha, Fernandes and Soares [16] features an application of the Volume Algorithm to solve the dual Lagrangean problem associated to the formulation MC-ATSP. They test the procedure on several TSPLIB instances, which includes the ones used in the present work. The number of iterations vary from instance to instance hanging from 1000 to 10000, depending on the size of the instance. They do not report dual bounds for the ftv170 instance and therefore this instance is not included in the comparison. The average relative value of the best bounds obtained with the Volume Algorithm (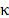 ) in comparison with the MC-RCP procedure (
) in comparison with the MC-RCP procedure (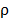 ) is 17%, and the standard deviation is 28.75%. Considering the number of iterations required to the MC-RCP, the relax and cut procedure proposed in this work provides good dual bounds with a reduced computational effort. The bounds obtained with the MC-RCP and the associated relaxed solution could be used as a starting point to the Volume Algorithm. This might improve the performance of the algorithm in terms of reducing the total number of iterations and execution time.
) is 17%, and the standard deviation is 28.75%. Considering the number of iterations required to the MC-RCP, the relax and cut procedure proposed in this work provides good dual bounds with a reduced computational effort. The bounds obtained with the MC-RCP and the associated relaxed solution could be used as a starting point to the Volume Algorithm. This might improve the performance of the algorithm in terms of reducing the total number of iterations and execution time.
4. Concluding Remarks
]]> In this work, we studied two procedures to obtain dual bounds to the Asymmetric traveling salesman problem. The procedures are based on the relax and cut method that starting from the optimal solution to the assignment problem, identifies violated inequalities and dualizes them to build a Lagrangean function. Two classes of valid inequalities are used. The CS-RCP procedure is based on cut set subtour elimination constraints, and the MC-RCP procedure is based on the multi-commodity subtour elimination constraints.The procedures were tested on a set of instances from the TSPLIB. The computational results obtained with both procedures are encouraging. The quality of the bounds given by the two algorithms is similar. The CPU time required to compute the dual bounds with both the CS-RCP and MC-RCP are small when compared to the time necessary to obtain dual bounds solving the linear relaxation of the MC-ATSP formulation.
The formulation CS-ATSP and MC-ATSP are equivalent and give the same linear relaxation values. Still, a combination of the two types of subtour elimination constraints can be useful in a relax and cut procedure. They could be used sequentially, since the valid inequalities identified are distinct. The matrix of reduced costs resulting from the CS-RCP can be used as starting point for the MC-RCP. The implementation of the CS-RCP was important for two reasons: it served as a benchmark for the MC-RCP and updated the work of Balas and Christofides [2] since it was tested with instances of the TSPLIB while in the original work it was tested only with random data.
The dual bounds obtained with the relax and cut procedures presented here can be useful to speed up the solution of large instances of the ATSP by the implicit enumeration methods present in commercial and noncommercial solvers.
Acknowledgements
This research was partly supported by the Brazilian research agencies Capes, CNPq (306194/2012-0) and Fapesp (2013/07375-0, 2010/10133-0). It also received partial support from the RFBR (12-01-00893) and CONACYT (167019). Special thanks are due to Michelli Maldonado that collaborated in the early stages of this research.
References
[1] Álvarez, P.J., Calderón, C.A.G. and Calderón, G.G., Route optimization of urban public transportation. DYNA, 88 (180), pp. 41-49, 2013. [ Links ]
[2] Balas, E., Christofides, N., A restricted Lagragean approach to the traveling salesman problem, Mathematical Programming, 21, pp. 19-46, 1981. DOI: 10.1007/BF01584228 [ Links ]
[3] Dantzig G., Fulkerson R. and Johnson S., Solution of a large-scale traveling-salesman problem, Operations Research 2, pp. 393-410, 1954. DOI: 10.1287/opre.2.4.393 [ Links ]
[4] De Souza, C.C. and Cavalcante, V.F., Exact algorithms for the Vertex separator problem in graphs, Networks 57 (3), pp. 212-230, 2011. DOI: 10.1002/net.20420 [ Links ]
[5] Escudero, L.F., Guinard, M. and Malik, K., A Lagrangian relax-and-cut approach for the sequential ordering problem with precedence relationships, Annals of Operations Research 50, pp. 219-237, 1994. DOI: 10.1007/BF02085641 [ Links ]
[6] Fischetti, M., Salvagnin, D., A relax-and-cut framework for gomory mixed-integer cuts, Mathematical Programming Computation 3 (2), pp. 79-102, 2011. DOI: 10.1007/s12532-011-0024-x [ Links ]
[7] Gavish, B., Augmented Lagrangean based algorithms for centralized network design, IEEE Transactions on Communications 33, pp. 1247-1257, 1985. DOI: 10.1109/TCOM.1985.1096250 [ Links ]
[8] Guignard, M., Lagrangean relaxation, Top 11 (2), pp. 151-228, 2003. DOI: 10.1109/TCOM.1985.1096250 [ Links ]
[9] Kawashima, M.S., Relax and cut: Limitantes duais para o problema do caixeiro viajante, MSc. Thesis, UNESP - Universidade Estadual Paulista, São José do Rio Preto, Brasil, 2014. [ Links ]
]]>[10] Kawashima, M.S., Rangel, S,. Litvinchev, I. and Infante, L., Relax and cut: Dual bounds for the traveling salesman problem. Memorias del CILOG 2014. San Luis Potosí, México: Mexican Logistics & Supply Chain Association, 2014. [ Links ]
[11] Lucena, A., Steiner problem in graphs: Lagrangean relaxation and cutting planes, COAL Bulletin 21, pp. 2-8, 1993. [ Links ]
[12] Lucena, A., Non-Delayed relax and cut algorithms, Annals of Operations Research 140, pp. 375-410, 2005. DOI: 10.1007/s10479-005-3977-1 [ Links ]
[13] Maldonado. M., Rangel, S., Ferreira, D., A Study of different subsequence elimination strategies for the soft drink production planning, Journal of Applied Research and Technology 12, 631-641, 2014. DOI: 10.1016/S1665-6423(14)70080-X [ Links ]
[14] Öncan, T., Altinel, I.K., Laporte G., A comparative analysis of several asymmetric traveling salesman problem formulations, Computers &Operations Research, 36, pp. 637-654, 2009. DOI: 10.1016/j.cor.2007.11.008 [ Links ]
[15] Reinelt, G., TSPLIB - A traveling salesman problem library, ORSA Journal Computing, [on line] 3, pp. 376-384, 1991. Available at: https://www.iwr.uniheidelberg.de/groups/comopt/software/TSPLIB95/, last visited in 11/04/2014 [ Links ]
[16] Rocha, A.N., Fernandes, E.M.G.P. and Soares, J., Aplicação do algoritmo volumétrico à resolução aproximada e exacta do problema do caixeiro viajante assimétrico, Investigação Operacional 25 (2), pp. 277-294, 2005. [ Links ]
]]>[17] Serna, M.D.A., Jaimes, W.A. and Cortes, J.A.Z., Commodities distribution using alternative types of transport. A study in the Colombian bread SME's. DYNA, 77 (163), pp. 222-233, 2010. [ Links ]
[18] Sherali, H.D. and Smith, J.C., Dynamic Lagrangean dual and reduced RLT constructs for solving 0-1 mixed-integer programs, Top 20 (1), pp. 173-189, 2012. DOI: 10.1007/s11750-011-0199-3 [ Links ]
M.S. Kawashima, completed his MSc. degree from the Universidade Estadual Paulista (UNESP), Brazil. His research focuses on the study of large-scale combinatorial optimization problems.
S. Rangel, is an associate professor at UNESP, Brazil. She completed her PhD. at Brunel University. Since then she has been mainly involved in the study of large-scale combinatorial optimization problems. The focus has been on building efficient models for practical applications, and developing solving techniques based on hybrid algorithms that combine several methods such as partial enumeration, cutting planes, heuristics, pre-processing and aggregation/ decomposition.
I. Litvinchev, is a professor at UANL, Mexico and a Head of Department at Computing Centre, Russian Academy of Sciences (CCRAS), Moscow. He completed his MSc. degree from the Moscow Institute of Physics and Technology (Fizteh), PhD. and Dr. Sci. (Habilitation) degrees in systems modeling and optimization from CCRAS. His research focuses on large-scale system modeling, optimization, and control with applications to logistics and supply chain management. Dr. Litvinchev is a member of Russian Academy of Natural Sciences and Mexican Academy of Sciences.
L. Infante, completed his MSc. degree from the Universidad Autónoma de Nuevo León (UANL), México. His research focuses on the study of large-scale combinatorial optimization problems.
]]>