
Burst erasure correction using LDPC codes constructed on base matrices generated by matched groups, nested polygons and superposed circulant matrices
Corrección de borrado en ráfaga utilizando códigosLDPC construidos sobre matrices generadas por grupos combinados, polígonos anidados y matrices circulantes superpuestas
Cassio André Sousa-da Silva a & Evaldo Pelaes b
a Facultad de Matematica, Universidad Federal de Oeste de Pará, Santarém, Brasil. cassio@ufpa.br
b Departamento de Engenharia Elétrica, Universidade Federal de Pará, Belém, Brasil. pelaes@ufpa.br
Received: July 4th, 2015. Received in revised form: January 18th, 2016. Accepted: February 18th, 2016.
]]>This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
Abstract
This article proposes procedures for the construction of base matrices grounded in algebra and geometry. These base matrices serve as a platform to generate the parity check matrices for debugging in bursts erasure through LDPC codes by superposing the base matrices and movements of circulant matrices. The construction of the matrices is performed by concatenation as it is easy to implement and has a lower randomness. To demonstrate the potential of the technique, we developed a number of simulations using low complexity encoding as well as the sum-product algorithm. Several LDPC codes (matrices) were generated and the results were compared with other approaches. We also present the outcomes of erasure recovery simulations that result from the transmission of an image through a noisy channel.
Keywords: Low-density parity-check codes, burst erasure correcting codes, burst erasure channels, erasure-correcting codes, matrix by superposition, Information and Communications Technologies (ICT's).
Resumen
En este artículo son propuestos procedimientos para la construcción de matrices base embazado en el álgebra moderna y en la geometría. Estas matrices sirven de plataforma para generar las matrices de verificación de paridad en la corrección de borrado en ráfaga a través de códigos LDPC, por medio de superposición en las matrices base y movimientos de las matrices circulantes. La construcción de las matrices es realizada por concatenación, siendo de fácil implementación y de menor aleatoriedad. Para demonstrar el potencial de la técnica, fue elaborado un conjunto de simulaciones que utiliza codificación de baja complejidad, bien como algoritmo soma y producto. Fueron generados varios códigos LDPC (matrices) y los resultados obtenidos comparados con otros abordajes. Son también presentados los resultados de la simulación de la recuperación de borrados resultantes de la transmisión de una imagen a través de un canal ruidoso.
Palabras clave: Códigos de baja densidad, Códigos de corrección de borrado en ráfaga, Canales de borrado de ráfaga, Códigos de La corrección de errores, matrices superpuestas, Tecnologías de la Información y Comunicaciones (TIC's)
1. Introduction
]]> Currently, information technologies (ICTs) are active in all the social events that use media as a form of communication. From large corporate business [1-3] to hydrographic ecosystems analysis [4], ICTs are used as a great way to communicate and present scientific conclusions. The huge explosion of the use of these electronic media is partly due to the popularity of HDTV [5] and the transmission of data via the internet. Over the last few years a new modality has been becoming more popular in these transmissions and contributes to a real communication: real-time transmissions. The goal of a communication system is to transmit a message through a communication channel so that the receiver can retrieve the message with a given criterion of fidelity. Nevertheless, a real communication system faces various problems, especially certain disturbances that are introduced by the media. These generate erasure during transmission across the channel due to several physical variables imposed by the channel [1].Recent research suggests that on a variety of networks, packet losses occur in bursts [7-10]. As such, many bits lost during the transmission of messages through the channel cause long decoding delays and other message processing in the receiver. The application of LDPC codes to correct these lost and unrecognizable bits in burst has been widely used [6,11-12].
To detect unrecognizable symbols produced by deleting channels, block codes are typically used as error detection codes in memoryless channels. Recently, LDPC codes have been used for erasure-correcting memory [15-16]. Low-Density Parity-Check code (LDPC) is a linear block code C (n, k) with a rate k/n that is defined by a sparse parity check matrix H (n-k) × n. This uses the interactive algorithm for decoding known as belief propagation or sum-product (SP) [16] that is currently being used to correct erasure in bursts [17,11-14].
In this work, we consider a burst erasure channel (BuEC) in channels with memory, as is defined in [7]. The transmitter sends n binary symbols through the channel, but in the receiver, the received symbols ri (0 ≤ i ≤ n-1) can be deleted. Since we assume an ideal detector for burst noise, these burst noises give rise to burst erasures. We can measure the effectiveness of a given burst noise code by a single parameter: the maximum resolvable erasure-burst length, Lmax. This parameter is defined as the maximum length of deletion, and as so the interactive decoding is able to retrieve it regardless of its position within the codeword [25]. Furthermore, we assume that the deletions occur in a single burst. Yang and Ryan [8] developed an efficient algorithm to determine Lmax in terms of bits. The efficiency h(H) of an n-length code with rate k/n is defined as the ratio between its Lmax and the information transmitted, namely:
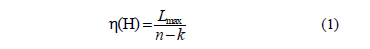
In this paper we investigate the possibility of constructing an LDPC code capable of performing a successful decoding of erasure and bursts through the construction of a parity-check matrix H less random. In order to do this, the burst erasure efficiency of the check matrix h (H) is determined from the concatenation of new base matrices superposed by circulant matrices. In Section 2, we present the mathematical fundaments used in the construction of the binary matrix that will be used as a platform matrix. In section 3, we present the procedures for constructing the platform matrix and the algorithms that generate the parity-check matrix used for decoding LDPC codes. Finally, Section 4 details findings and conclusions found in the analysis and performance of LDPC codes that were implemented by the proposed matrices.
2. Base matrices
The base matrix is a sparse binary matrix that uses the superposition of other matrices in its non-zero entries to construct the parity-check matrix of a code [19]. To decode burst errors, in this work, we propose two base matrices that are grounded on the construction of geometrically uniform signs matched with groups [20], [22] and on the formation of Nested Polygons based on Davis [23].
A signal constellation S is any discrete subset in Rn. The elements of a signal constellation S are called signal points. A Euclidian-space code is a subset of, SI where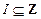 .
.
The signal constellations obtained via rotation are known as rotated signal constellations. In n-dimensional Euclidean-spaces the constellations can be characterized as a lattice in the cubic form of the type Zn. Thus, an x point of the rotated constellation is obtained by the action of an P-matrix in the u;-vector, that is, the set of points {x = uP, u ∈ Zn}.
Loeliger in [20] and Forney in [22] proposed algebraic procedures to obtain 2PSK 3PSK, 4PSK signal constellations matched to additive groups from the additive structure of the signal fields that are matched to groups (D3, D4, Z6). These procedures were based on the classical results of modern algebra (Lattices). It is assumed that the reader is familiar with notions like group theory, subgroups, lateral classes, homomorphisms, etc., which comprise the theoretical background that is necessary to be able to comprehend this text.
A signal constellation S is geometrically uniform [19], if s1, s2 ∈ S exist j ∈ Isom(Rn) such that j(s1) = s2 and j(s) = s. If G(S) = {j ∈ Isom(Rn): j(s) = s}, then S is an orbit of any point s0 ∈ S under G(S), that is,
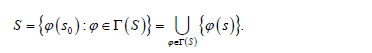
A block code with the same type of energy [23] is any finite signal constellation on a sphere that generates Rn as a vector space, which we denote by a. The number of signal points or codeword end d isthe quadratic minimum distance of S. In particular, when an Sspherical code is geometrically uniform we say that S is a uniform constellation. This is introduced by Slepian in [23] who uses the group codes name for theGaussian channel; it is generalized by Forney [19] for any signal constellation.
A signal constellation S is matched with a group G if there is a µ-mapping µ of G over S, such that [17]:
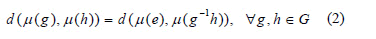
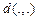 is the quadratic Euclidean distance and "e" describes the unit of G..
is the quadratic Euclidean distance and "e" describes the unit of G.. The µ-mapping is called a matched mapping. When µ-mapping is a matched labelling, that is, if G is isomorphic to G(S), then µ is an isometric labelling. Let be C a linear code over Zm of length n, [17] then we can define the following:
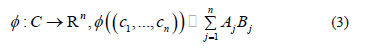
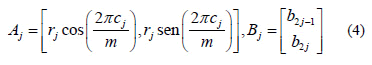
and {b1, b2,..., b2n} is an orthonormal base in R2. Matrices Aj and Bj are coordinates of constellation points. Note that rj is just an energy parameter that depends on j but not on the codeword. In general, we take r j= 1, for every j = 1,...,n. The mapping f is called canonical mapping.
The first base matrix (5) is constructed by connecting the geometric signal points of the vertices of the antiprism matched with Z6. [20] shows this algebraic geometric association starting from steps linking the points of polyhedra (prism and antiprism) to the d-chain developed from a subgroup of G. The matrix (5) expresses, in general, the mapping applied between the matched antiprism with a signal constellation (remainder classes or dihedrons) and a canonical base of Rn. Fig. 1 shows the matched antiprism with the Z6 group.
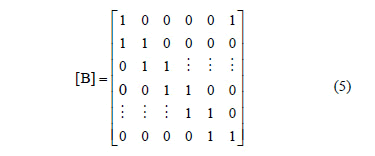
The second matrix is based on the construction of a "nest" formed by an octagon and two squares. The idea of "nest" comes from the proportional division of the sides of a polygon. Davis [21] constructs these nested polygons by connecting the dots of this division; the second polygon is formed by connecting the points generated by the first polygon, the third polygon is constructed analogously, and so on. Fig. 2 shows the nest formed by two squares and one octagon, the division ratio of which is ½.The matrix is associated with that nest.
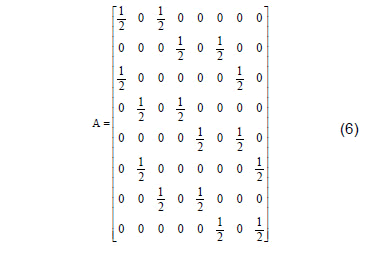
Take the matrix B=2A and then construct a C8X6 matrix that operates at the B columns. Using the notation Cj, j = {1,…,6}, we denote the six columns of the matrix C. Do: C1 = B1, C3 = B4, C5 = B7, C6 = B8e B2 + B3 = C2, B5 + B6 = C4 and obtain the following matrix:
]]>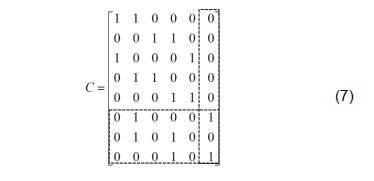
Deleting the sixth column and the last three rows of this matrix gives the following binary matrix:
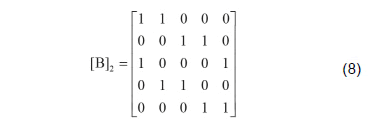
3. Construction of a Platform Matrix and a Check Matrix
The check-parity matrix is the key element to determine the Lmax [14] when correcting burst erasure. The construction of the parity-check matrix made by Galague [16] is almost random, but parity matrices consisting of circulant matrices are systematic. They have been studied by several authors to design LDPC erasure codes in bursts with good efficiency [12], [24], [11]. In this section, we present a procedure to design LDPC codes to correct erasures in bursts using a superposition of matrices [19]. A combination of three types of sparse matrices is used: the base matrix, the platform matrix and the circulant matrix.
Let ,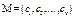 a circulant matrix of order v. When c1 = 1 and the other values are zero, the M circulant is the identity matrix of order v. Thus, the vector
a circulant matrix of order v. When c1 = 1 and the other values are zero, the M circulant is the identity matrix of order v. Thus, the vector 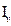 = (1, 0, ..., 0), with
= (1, 0, ..., 0), with 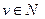 will be the identity matrix generator. Using the notation
will be the identity matrix generator. Using the notation 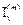 with
with 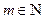 , it is possible to describe modv circulating movements in the identity matrix
, it is possible to describe modv circulating movements in the identity matrix 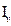 . The matrix 0 represents the zero matrix of order v. The following matrix
. The matrix 0 represents the zero matrix of order v. The following matrix 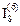 represents a circulant identity matrix of size 8 and movement m = 6. The zero-elements were discarded.
represents a circulant identity matrix of size 8 and movement m = 6. The zero-elements were discarded.
The platform matrix is an auxiliary matrix that is used to construct the parity-check matrix. The technique developed for the construction of the platform matrix is that proposed by [14], which is made of superposed sub-matrices in non-zero entries of the binary matrix. In this paper the sub-matrices are called client matrices and the platform matrix is developed from the composition of two client matrices: the circulant matrix and the zero matrix, both of order v.
A 4-cycle occurs in H if two columns of H contain non-zero entries in the same two rows. Thus, concatenating and alternating circulating matrices and null matrices in the final construction of the parity-check matrix, the following algorithms will give us 4-cycle free matrices. Avoiding 4-cycles can improve the performance of the decoded interaction and therefore the decoding burst [11].
Example 1: The following is the platform matrix 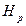 that was constructed from the random superposition of the client matrix
that was constructed from the random superposition of the client matrix 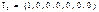 in the base matrix Hb in a 5-dimension formed by the elements: Hb (i, j) = 1 for i = j with
in the base matrix Hb in a 5-dimension formed by the elements: Hb (i, j) = 1 for i = j with 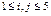 in the first diagonal and Hb(2,1)=Hb(3,2)=Hb(4,3)=Hb(5,4)=1 in the diagonal just below and other null elements. In the first diagonal of Hp
in the first diagonal and Hb(2,1)=Hb(3,2)=Hb(4,3)=Hb(5,4)=1 in the diagonal just below and other null elements. In the first diagonal of Hp 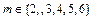 , matrices I(2) and I(6) represent the movements 2mod8 and 6mod8 circulant of I8. Zero elements were discarded.
, matrices I(2) and I(6) represent the movements 2mod8 and 6mod8 circulant of I8. Zero elements were discarded.
We will now present two algorithms that generate parity-check matrices using the binary matrices developed in section II. The first algorithm was developed to analyze and check performance of the following codes: LDPC C1(500,250); C2(1800,1200); C3(3000,1500); C4 (4158,3465); C5(3750,3125), and the second algorithm was developed to construct the following codes: LDPC C6(1500,1200); C7 (4200,3600). The algorithm choice is subject to the length of the code. Algorithm 2 is mainly used for codes with multiple dimension values of 5. Algorithm 1 is mainly used for other dimensions.
Algorithm-1. This algorithm constructs a parity-check matrix of dimension Npv and rate 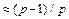 from the concatenation of p copies of the base matrix (5) of dimension N. Given a sequence
from the concatenation of p copies of the base matrix (5) of dimension N. Given a sequence 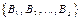 of p copies (5), the first platform H1 is created by superposition in B1, the second H2 by superposition on B2, and so on.
of p copies (5), the first platform H1 is created by superposition in B1, the second H2 by superposition on B2, and so on.
Step 1: Consider
binary matrices of (5), with dimension
Step 2: Construction of platform matrix H1:
A) In non-zero entries of the main diagonal of B1 substitute by
B) In non-zero entries of the diagonal immediately below the main diagonal of B1 substitute by
and make
in at least one of the elements
Step 3: Construction of platform matrices
]]>:
A) In non-zero entries of the main diagonal superpose
m is selected so that the sum of the movements of
is a multiple of N.
B) In non-zero entries of the diagonal immediately below the main diagonal, l repeat step 2.B
Step 4: Superpose the matrix 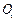 in the zero elements of
in the zero elements of 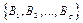
Step 5: In the free element in matrices 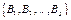 , superpose
, superpose 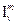 with any movement.
with any movement.
Step 6: Construct parity-check matrix 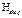 free of 4-cycles, dimension
free of 4-cycles, dimension 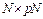 and rate
and rate 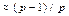 concatenating
concatenating 
Example 2: Next, we have , with
, with  platform matrices for N=5. The D1D2D3D4D5 notation represents the main diagonal of Hi, while S1S2S3S4 represents the diagonal immediately below the main one, F indicates the free element. Zero elements were discarded. Table 1 shows some movements that were proposed in the client matrix I.
platform matrices for N=5. The D1D2D3D4D5 notation represents the main diagonal of Hi, while S1S2S3S4 represents the diagonal immediately below the main one, F indicates the free element. Zero elements were discarded. Table 1 shows some movements that were proposed in the client matrix I.
In the construction of the LDPC code C1(500,250) the concatenations H1H2, H1H3 and H1H4 (v = 50, p = 2, rate 0.5) and H1H2H3H4 (v = 25, p = 4) are produced. For the construction of code C2(1800,1200) (v = 120, p = 3, rate 0.66) we used the concatenations H1H2H3 and H1H3H4 and in the construction of code C3(3000,1500) we used H1H4 (v = 300, p = 2, rate 0.5). With N=5 and N=3 we construct analogously with small variations in client matrices, codes LDPC C5(3750,3125) (v = 125, p = 6, rate 0.833), and C4 (4158,3465) (v = 231, p = 6, rate = 0.833) respectively. Next, we have check matrices Hb1 = [H1H4] for LDPC code C1(500,250) and Hb2=[P1P2] (P1, P2 auxiliaries matrices) for LDPC code C4 (4158,3465). Zero elements were discarded.
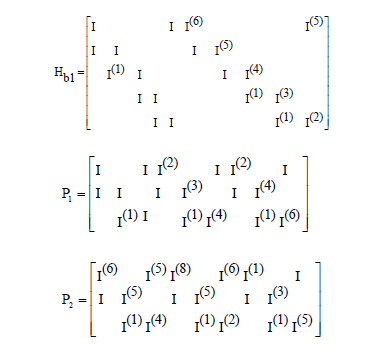
Algorithm-2. This algorithm constructs a parity-check matrix with dimension Npv and rate 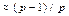 from the concatenation of p copies of the platform matrix (8). Given a sequence
from the concatenation of p copies of the platform matrix (8). Given a sequence 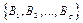 of p copies of (8), we have:
of p copies of (8), we have:
Step 1: Take 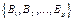 p copies of binary matrices of (8).
p copies of binary matrices of (8).
Step 2: Construct the platform matrices 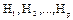 attributing matrices s
attributing matrices s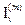 by superposition in
by superposition in 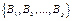 so that the sum of random movements is mod5.
so that the sum of random movements is mod5.
Step 3: Superpose matrix 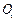 in the null elements of
in the null elements of 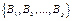
Step 4: Construct the parity-check matrix 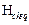 free of 4-cycles, dimension
free of 4-cycles, dimension 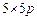 and rate
and rate 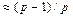 concatenating
concatenating 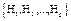
Example 3: Next, we have five platform matrices 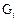 built from algorithm 2, whose elements are denoted by letters A,B,C,D,E,F,J,L,M, which also designate the superposed client matrices. Zero elements were discarded, see Table 2. The code LDPC C6(1500,1200) was constructed from the following concatenations: G1G1G1G1G1, G1G2G2G2G2 and G2G2G2G2G2 (v=60, p=5, rate 0.8) and code LDPC C7(4200,3600) by using the concatenations G1G1G2G2G3G3G3 and G1G2G3G4G5G5G4 (v=24,p=7, rate 0.857).
built from algorithm 2, whose elements are denoted by letters A,B,C,D,E,F,J,L,M, which also designate the superposed client matrices. Zero elements were discarded, see Table 2. The code LDPC C6(1500,1200) was constructed from the following concatenations: G1G1G1G1G1, G1G2G2G2G2 and G2G2G2G2G2 (v=60, p=5, rate 0.8) and code LDPC C7(4200,3600) by using the concatenations G1G1G2G2G3G3G3 and G1G2G3G4G5G5G4 (v=24,p=7, rate 0.857).
]]> 4. Simulation and comparison of results
The purpose of this section is to show that the LDPC codes developed from algorithms 1 and 2 perform well when correcting burst erasure in BuEC and also to show that the parity-check matrices developed from the constructions have an excellent performance in correcting these erasures.
4.1. Simulations in BuEC
The motivation for considering a burst erasure channel to model channels with memory is their simplicity as well as the fact that the bit loss of information, often sent, occurs in them. Any system where the receiver is capable of distinguishing long losses in bits can treat this period of failures as a burst erasure channel. Simulations were produced in BuEC with values between -2 and 20 decibels. An SP algorithm with soft decision was used with an error probability p = 0.01, with 100 interactions. To analyze the performance of the LDPC codes, the parity-check matrices used were constructed from algorithms 1 and 2 from examples 2 and 3. For code C1(500,250), rate 0.5, we have four concatenations proposed by algorithm1: H1H2, H1H3, H1H4 and H1H2H3H4 with Lmax 240, 241, 248 and 118 bits, respectively. It is observed that H1H4 has the best efficiency (99.2 %). It can be seen that H2, H3, H4 have few differences in the movements of client matrices contained in the main diagonal, however, H4 has a significantly different movement in its spare element F=I(5) relative to the free elements of H2 and H3, i.e. F=I.
Fig. 3 shows the code efficiency proposed in algorithm 1 when correcting burst erasure.
For code C2(1800, 1200) we proposed the concatenations of the matrices H1H2H3, H1H2H4 developed in example 2 with Lmax 572 and 576 bits respectively. The best yield observed is the concatenation H1H2H4 which, in turn, has the matrix I(5) as a client matrix in its free element. In a preliminary conclusion, it may be said that the most "abrupt" movement of the free element is responsible for better code performance.
For code C6(1500,1200), the concatenations proposed were the ones developed in example 3: G1G1G1G1G1, G1G2G2G2G2 and G2G2G2G2G2 (v = 60, p = 5, rate 0.8) with Lmax 290, 292, 296 bits respectively. The last concatenation obtained the best yield (98%). For code C7(4200, 3600), we obtained the following concatenations: G1G1G2G2G3G3G3 and G1G2G3G4G5G5G4 (v = 24, p = 7, rate 0.857) with Lmax 582, 580 bits respectively. The last concatenation obtained the best yield (96%). Fig. 4 shows the efficiency of the proposed code in Algorithm 2 when correcting burst erasure.
In any of the constructed codes the one that presents the best performance is the code which has the client matrix with a number that indicates the larger movement: I(6) in C6(1500,1200) and I(5) and I(6) in C7(4200, 3600). This indicates that the larger the movement of the client matrix is the better the decoding performance.
]]> For large bursts in BuEC, LDPC codes have been an efficient corrector for errors and erasures [20-23]. Table 3 compares the LDPC codes' correction properties for burst erasure that were constructed in this article with previous results. Fig. 5 shows the performance of an LDPC code with a length of 4170 and rate of 0833 when correcting burst errors via algorithms 1 and 2 (N = 5, v = 139, p = 6) in the classic bursty channel. Note that the codes randomly constructed and simulated here are not truly random as they have been optimized to avoid repeated columns and cycles of length 4, when possible.4.2. Erasure recovery in a Noisy Channel using the proposed code - Simulation
We will now present the transmission simulations results through a noisy channel. In the simulation, we used the Lena.gif which has a size of 512X512 (262.144 pixels) and an LDPC code with parity-check matrices developed by algorithms 1 and 2. This channel sent a codeword with a length of 1512 and a rate of 0.8, which was adapted to the encoding software. The noisy channel introduces losses of bits in a random point in the codeword and the erased bits are recovered in the receiver.
The Lena.gif (512x512) original image is displayed in Fig. 6(a). The probability of channel erasure varied from 0.01 to 0.99 in increments of 0.05. In this range, the number of lost or erased bits is approximately 20% to 50% of the total amount of bits of the codeword. Finally, with a 0.99 erasure probability (extremely hostile channel) we obtain a lost bit in a range from 90% to 98% of the codeword at the output. Fig. (6) shows Lena's image in the output of the channel with the information erased by the channel
The image obtained in the channel output goes through a recovery process by means of LDPC codes that use algorithms 1 and 2 in the development of parity-check matrices to decode by sum-product. Fig. 7(a) shows the image that was retrieved using the concatenated matrices with free element F=I. It can be seen that the decoder does not recover 5% of the initial erasure track, and in the most hostile track the decoder does not recover 12% of the bits transmitted by codewords. Fig. 7(b) shows the image retrieved when F=I(5). In this case, regardless of the erasure track, the decoder recovers 98% of the lost bits. When client matrices I(5) and I(6) were used in algorithm 2, an efficiency of 98% recovery of lost bits is achieved, as Fig. 7(c) shows. Thus, we obtained the following result: we can see that the best performance for decoding comes when comparing the performance of the codes for which the values F=I and F=I(5) are used for the free element F in the concatenated matrices, produced by the algorithm 1, F=I(5).
]]> 5. Conclusion
In this paper, two algorithms were presented to develop parity-check matrices to generate LDPC codes based on the concatenation of base matrices superposed by circulant client matrices weight 2. The simulations showed that the codes generated by parity-check matrices that were obtained from the proposed base matrices and by the movements of client matrices showed a good efficiency in terms of the correction of burst erasures. Comparing H1H2, H1H3 and H1H4, it can be seen that the movement of the free element I(5) of H4 was responsible for the improvement and efficiency of the code. We can also arrive at this conclusion by comparing the concatenations proposed in example 2 by using the matrix I(6) as a client. Table 3 shows that Algorithm-2 (p = 6, v = 550), as a client, achieves the same efficiency as the construction proposed by Sara [11]. Although algorithms 1 and 2 are designed with  dimension matrices, it was possible to evaluate simulations with different dimensions because the vector of circulant matrices enables the combination of numbers that express non-multiple dimensions of 5. The proposed algorithms were used to generate LDPC codes to simulate erasure correction in Lena's image, they were transmitted through a noisy channel, and their results were satisfactory.
dimension matrices, it was possible to evaluate simulations with different dimensions because the vector of circulant matrices enables the combination of numbers that express non-multiple dimensions of 5. The proposed algorithms were used to generate LDPC codes to simulate erasure correction in Lena's image, they were transmitted through a noisy channel, and their results were satisfactory.
Acknowledgements
We would like to thank the support of Federal University of Pará and Federal University of Western Pará for their help with this work.
References
[1] Riascos-Erazo, S.C., A model for assessing information technology effectiveness in the business environment, Ingeniería e Investigación. [Online]. 28(2), pp 158-166, 2010. Available at: http://www.revistas.unal.edu.co/index.php/ingeinv/article/view/14905 [ Links ]
[2] Martínez-Roso, R., El papel de la comunicación en los sistemas generales. Ingeniería e Investigación. [Online]. 22, pp. 68-71, 2012. Available at: http://www.revistas.unal.edu.co/index.php/ingeinv/article/view/20668 [ Links ]
[3] Correa-Espinal, A., Gómez-Montoya, R.A., Tegnologías de la información en la cadena de suministro. DYNA, [Online], 76(157), pp. 37-48, 2009. Available at: http://www.revistas.unal.edu.co/index.php/dyna/article/view/9551/11475 [ Links ]
[4] Manrique-Losada, B., Echeverri-Arias, J. and Peláz-Rodriguez, M., Hydroinformatics' contribution to Amazonian water resources and ecosystem management. Ingeniería e Investigación, [Online], 31(1), pp. 108-116, 2011. Available at: http://www.revistas.unal.edu.co/index.php/ingeinv/article/view/20532/35684 [ Links ]
[5] Moreno-López, G.A. and Jiménez-Builes, J.A., Cycle of PDCA T-learing model and its application on interactive digital TV. DYNA, [Online], 79(173), pp. 61-70, 2012. Available at: http://dyna.medellin.unal.edu.co/en/verPDF.php?id_articulo=a07v79n173-II&tipo=articulo&id=173-II [ Links ]
[6] Zhihua, D. and Zhen, J., LDPC codes by circulant decomposition based on difference family, Proceedings of the International MultiConference of Engineers and Computer Scientists, [Online]. Vol I, IMECS, March 18-20, Hong Kong, 2009. Available at: http://www.iaeng.org/publication/IMECS2009/IMECS2009_pp384-386.pdf [ Links ]
[7] Forney, G.D., Burst-correcting codes for the classic bursty channel, IEEE Trans. Commun., 19(5), pp. 772-781, 1971. DOI: 10.1109/TCOM.1971.1090719 [ Links ]
[8] Yang, M., Ryan, W. and Li, Y., Design of efficiently encodable moderate length high-rate irregular LDPC codes, IEEE Trans. Communications, 52(4), pp. 564-571, 2004. DOI: 10.1109/TCOMM.2004.826367 [ Links ]
[9] M. Yang, W. Ryan, Performance of efficiently encodable low-density parity-check codes in noise bursts on the EPR4 channel, IEEE Trans. Magn., 40(2), pp. 507-512, 2004. DOI: 10.1109/TMAG.2004.824125 [ Links ]
[10] MacKay, D.J.C., Good error-correcting codes based on very sparse matrices, IEEE Trans. Inform. Theory, 45(2), pp. 399-431, 1999. DOI: 10.1109/18.748992 [ Links ]
[11] Johnson, S.J., Burst erasure correcting LDPC codes, IEEE Trans. Commun., 57(3), pp. 641-652, 2009. DOI: 10.1109/TCOMM.2009.03.060468 [ Links ]
[12] Hosoya, G., Yagi, H., Matsushima, T. and Hirasawa, S., A modification method for constructing low-density parity-check codes for burst erasures, ICICE Trans. Fundamentals, E89-A(10), pp. 2501-2509, 2006. DOI: 10.1093/ietfec/e89-a.10.2501 [ Links ]
[13] Tai, Y.Y., Lan, L., Zeng, L., Lin, S. and Abdel-Ghaffar, K.A.S., Algebraic construction of quasi-cyclic LDPC codes for the AWGN and erasure channels, IEEE Trans. Commun., 54(10), pp. 1765-1774, 2006. DOI: 10.1109/TCOMM.2006.881361 [ Links ]
[14] Paolini, E., Chiani, M. and Calzolari, G.P., Construction of near-pptimum burst erasure correcting low-density parity-check codes IEEE Trans. Inform. Theory, 57(5), pp. 1320-1328, 2009. DOI: 10.1109/TCOMM.2009.05.070047 [ Links ]
[15] Xu J. and Lin, S., A combinatoric superposition method for constructing LDPC codes, in Proc. International Symposium on Information Theory (ISIT'2003), Yokohama, Japan, June 2003, 30P. DOI: 10.1109/ISIT.2003.1228044 [ Links ]
[16] Gallager, R.G., Low-density parity-check codes, IRE Trans. Inform. Theory, IT-8(1), pp. 21-28, 1962. DOI: 10.1109/TIT.1962.1057683 [ Links ]
[17] Kan L., Aleksanda, K. and Erden, M., Fatih, construction of burst-erasure efficient LDPC codes for use with belief propagation decoding, Proc. IEEE 2010. DOI: 10.1109/ICC.2010.5502511 [ Links ]
[18] Peng, F., Yang, M. and Ryan, W.E., Simplified eIRA code design and performance analysis for correlated Rayleigh fading channels, IEEE Trans. Wireless Commun., 5(4), pp. 720-725, 2006. DOI: 10.1109/TWC.2006.1618918 [ Links ]
[19] Xu, J., Chen, L., Zeng, L.-Q., Lan, L. and Lin, S., Construction of low density parity-check codes by superposition, IEEE Trans. Commun., 53(2), pp. 243-251, 2005. DOI: 10.1109/TCOMM.2004.841966 [ Links ]
[20] Loeliger, H.A., Signal sets matched to grups, IEEE Trans. Inform. Theory, IT-37, pp. 1675-1682, 1991. DOI: 10.1109/18.104333 [ Links ]
[21] Davis, P.J., Circulant Matrices, Chelsea Publishing, New York, Press, 1994. [ Links ]
[22] Forney, Jr., G.D., Geometrically uniform codes,IEEE Trans. Inform. Theory, 37, pp. 1241-1260, 1991. DOI:10.1109/18.133243 [ Links ]
[23] Slepian, D., Group codes for gaussian channel, Bell Syst, Tech. J., 47, pp 575-602, 1969. DOI:10.1002/j.1538-7305.1968.tb02486.x [ Links ]
[24] Fossorier, M., Quasi-cyclic low density parity check codes from circulant permutation matrices, IEEE Trans. Inf. Theory, 8, pp. 1788-1793, 2004. DOI: 10.1109/TIT.2004.831841 [ Links ]
E.G. Pelaes, received his BSc. in Physics in 1977 and BSc. in Electrical Engineering in 1977, both from the Federal University of Pará, Brazil, his MSc. in Electrical Engineering in 1982 from the Pontific Catholic University of Rio de Janeiro, Brazil, and his PhD in Electrical Engineering in 1998 from UNICAMP University. He is currently an associated professor at the Federal University of Pará, Brazil. He has experience in Electric Engineering, with emphasis in Processing of Signals. His current research includes the following subjects: processing of signals, transformed wavelet and codification of images, models propagation, communications and quality of energy. ORCID: 0000-0001-8572-6131
C.A.S. Silva, received his BSc. in Mathematics in 1992 from the State University of Pará, Brazil, and his MSc in Pure Mathematics in 2003 from the Federal University of Paraíba, Brazil. He is an adjunct professor at the Federal University of Western Pará where he teaches Modern Algebra, Theory of Numbers, and History of Mathematics. ORCID: 0000-0002-9126-9560.
]]>