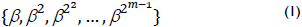
http://dx.doi.org/10.15446/ing.investig.v34n2.40542
P.C. Realpe-Muñoz1, V. Trujillo-Olaya2 and J. Velasco-Medina3
1 Paulo Cesar Realpe Muñoz. Bs in Physic Engineering, Universidad del Cauca, Colombia. M.Sc. in Electronics Engineering, Universidad del Valle, Colombia. Affiliation: Universidad del Valle, Colombia. E-mail: paulo.realpe@correounivalle.edu.co
2 Vladimir Trujillo Olaya. Bs in Electronic Engineering, Universidad del Valle, Colombia. M. Sc. in Electronics Engineering, Universidad del Valle, Colombia. Affiliation: Universidad del Valle, Colombia. E-mail: vladimir.trujillo@correounivalle.edu.co
3 Jaime Velasco Medina. B.S in Electrical Engineering, University del Valle, Colombia. Ph.D in Microelectronics, TIMA-INPG, France. Universidad del Valle, Colombia. E-mail: jaime.velasco@correounivalle.edu.co
ABSTRACT
This paper presents an efficient hardware implementation of cryptoprocessors that perform the scalar multiplication kP over a finite field GF(2163) using two digit-level multipliers. The finite field arithmetic operations were implemented using the Gaussian normal basis (GNB) representation, and the scalar multiplication kP was implemented using the Lopez-Dahab algorithm, the 2-non-adjacent form (2-NAF) halve-and-add algorithm and the w-τNAF method for Koblitz curves. The processors were designed using a VHDL description, synthesized on the Stratix-IV FPGA using Quartus II 12.0 and verified using SignalTAP II and Matlab. The simulation results show that the cryptoprocessors provide a very good performance when performing the scalar multiplication kP. In this case, the computation times of the multiplication kP using the Lopez-Dahab algorithm, 2-NAF halve-and-add algorithm and 16-τNAF method for Koblitz curves were 13.37 µs, 16.90 µs and 5.05 µs, respectively.
Keywords: elliptic curve cryptography, Gaussian normal basis, digit-level multiplier, scalar multiplication.
RESUMEN
En este trabajo se presenta la implementación eficiente en hardware de criptoprocesadores que permiten llevar a cabo la multiplicación escalar kP sobre el campo finito GF(2163) usando dos multiplicadores a nivel de digito. Las operaciones aritméticas de campo finito fueron implementadas usando la representación de bases normales Gaussianas (GNB), y la multiplicación escalar kP fue implementada usando el algoritmo de López-Dahab, el algoritmo de bisección de punto 2-NAF y el método w-τNAF para curvas de Koblitz. Los criptoprocesadores fueron diseñados usando descripción VHDL, sintetizados en el FPGA Stratix-IV usando Quartus II 12.0 y verificados usando SignalTAP II y Matlab. Los resultados de simulación muestran que los criptoprocesadores presentan un muy buen desempeño para llevar a cabo la multiplicación escalar kP. En este caso, los tiempos de computo de la multiplicación kP usando Lopez-Dahab, bisección de punto 2-NAF y 16-τNAF para curvas de Koblitz fueron 13.37 µs, 16.90 µs and 5.05 µs, respectivamente.
Palabras clave: criptografía de curva elíptica, bases normales Gaussianas, multiplicador a nivel de digito, multiplicación escalar.
Received: October 29th 2013 Accepted: February 25th 2014
Introduction
The use of computer networks and the steady increase in the number of users of these systems have driven the need to improve security for the storage and transmission of information. There are many applications that must ensure the privacy, integrity or authentication of the information stored or transmitted. The security of the applications has been resolved by using different cryptographic algorithms, which are used in private- or public-key cryptosystems.
]]> The security of public-key cryptosystems is based on mathematical problems that are computationally difficult to resolve, i.e., problems for which there are no known algorithms to resolve them in a practical time. Because of the high volume of information processed, electronic systems are required to perform the encryption and decryption processes in the shortest time possible without compromising the security. In this regard, hardware implementations of cryptographic algorithms have advantages, such as high speed, high security levels and low cost.One of the most important cryptosystems is the elliptic curve cryptosystem (ECC), proposed independently by Koblitz (Kobliz, 1987) and Miller (Miller, 1986). There have been several investigations of the theory and practice of this cryptosystem. The results of the investigations demonstrated the ability of these systems to encrypt information and concluded that this cryptosystem offers better security, efficiency and memory usage. The hardware implementations of ECCs have many advantages and are used in equipment such as ATMs, smart cards, telephones, and cell phones.
In elliptic curve cryptography, it is known that finding the discrete logarithm of a random elliptic curve element with respect to a publicly known base point, that is, the elliptic curve discrete logarithm problem or ECDLP, has high hardness. The entire security of the ECC depends on the ability to compute the scalar multiplication and the inability to compute the multiplicand given the original and product points. Furthermore, the finite-field size of the elliptic curve determines the computational complexity of the above problem.
Several works regarding scalar multiplication over a finite field GF(2m) have been proposed and implemented efficiently in hardware.
C. Rebeiro and D. Mukhopadhyay (Rebeiro and Mukhopadhyay, 2008) presented a cryptoprocessor with novel multiplication and inversion algorithms. J.Y. Lai, T.Y. Hung, K.H. Yang and C.T. Huang (Lai et al., 2010) proposed an architecture for elliptic curves along with the operation scheduling for the Montgomery scalar multiplication algorithm. B. Muthukumar and S. Jeevananthan (Muthukumar and Jeevanahthan, 2010) implemented an elliptic curve co-processor, which is a dual-field processor with a projective coordinate. A.K. Rahuman and G. Athisha (Rahuman and Athisha, 2010) presented an architecture using the Lopez-Dahab algorithm for the elliptic curve point multiplication and Gaussian normal basis (GNB) for field arithmetic over GF(2163). M. Amara and A. Siad (Amara and Siad, 2011) proposed an EC point multiplication processor intended for cryptographic applications such as digital signatures and key agreement protocols. X. Cui and J. Yang (Cui and Yang, 2012) implemented a processor that parallelizes the computations of the ECC at the bit-level and gains a considerable speed-up. The processor is fully implemented in hardware and supports key lengths of 113 bits, 163 bits and 193 bits.
In this context, we present in this work efficient hardware implementations of cryptoprocessors over GF(2163) using a GNB representation and the Lopez-Dahab algorithm, 2-NAF halve-and-add algorithm and w-τNAF method for Koblitz curves (Anomalous Binary Curves or ABC) with window sizes of 2, 4, 8 and 16 to perform the scalar multiplication kP.
The main contributions of this work are: (i) the hardware design of cryptoprocessors using the GNB over GF(2163) and three scalar multiplication algorithms (Lopez-Dahab, halve-and-add and w-τNAF method for Koblitz curves) to determine the best cryptoprocessor for embedded cryptographic applications. (ii) an efficient hardware implementation of cryptoprocessors based on the w-τNAF method with different window sizes for the Koblitz curves. They present the best trade-off between the computation time and area, obtaining a higher performance than the other cryptoprocessors reported in the literature. Additionally, they are very suitable for hardware cryptosystems.
Mathematical background
GNB representation
ANSI X9.62 (ANSI, 1999) describes the detailed specifications of the ECC protocols and uses the GNB to represent the finite field elements (NIST, 2000). An element over GF(2m) has the computational advantage of performing squaring very efficiently. However, multiplying distinct elements can be cumbersome. In this case, there are multiplication algorithms that make this operation both simpler and more efficient.
]]> A normal basis over GF(2m) is as follows:
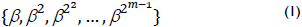
where β ∈ GF(2m) and any element A ∈ GF(2m) can be written as follows:
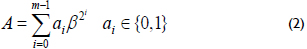
The type T of a GNB is a positive integer and measures the complexity of the multiplication operation with respect to that basis. Generally, the type T of a smaller value provides a more efficient multiplication. For a given m and T, the field GF(2m) can have at most one GNB of type T. A GNB exists whenever m is not divisible by 8. Let m and T be two positive integers. Then, the type T of a GNB over GF(2m) exists if and only if p =Tm+1 is prime.
If 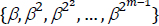 is a GNB over GF(2m), then the element
is a GNB over GF(2m), then the element 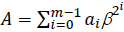 is represented by the binary string (a0a1a2 ... am-1), where ai ∈ {0,1}. In this case, the multiplicative identity element is represented by the bit string of all ones.
is represented by the binary string (a0a1a2 ... am-1), where ai ∈ {0,1}. In this case, the multiplicative identity element is represented by the bit string of all ones.
The additive identity element is represented by the bit string of all zeros. An important result for the GNB arithmetic is Fermat's Theorem. For all β ∈ GF(2m), then
]]>

This theorem is important for performing the squaring of an element over GF(2m).
Finite field arithmetic operations
The following arithmetic operations can be performed over GF(2m) when using a normal basis of type T.
Addition: If A = (a0a1a2...am-1) and B = (b0b1b2...bm-1) are elements over GF(2m), then A + B = C = (c0c1c2...cm-1), where ci= (ai + bi) mod 2.
Squaring: Let A = (a0a1a2...am-1) ∈ GF(2m), then
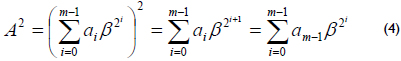
Based on Fermat's Theorem, , then
]]>
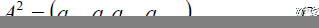
In this case, squaring is a simple rotation of the vector representation.
Multiplication: The multiplication C = A·B is based on the multiplication matrix R(m-1)XT (Masoleh, 2006). If A = (a0a1a2...am-1) and B = (b0b1b2...bm-1) are elements over GF(2m) and are represented using a GNB, then A·B = C = (c0c1c2...cm-1), where the coefficient c0 is given by equation (6)
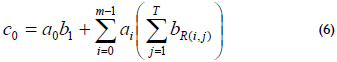
and R(i,j), 0 ≤ R(i,j) ≤ m-1, 1 ≤ i ≤ m-1, 1 ≤ j ≤ T denotes the (i, j)th element of the matrix. To obtain the ith coefficient of C, i.e., ci, add "i mod m" to all indices in (6).
Inversion: If A ≠ 0 and A ∈ GF(2m), the inverse of A is C ∈ GF(2m), and C is the only element of GF(2m) such that A·C = 1, i.e., C = A-1. The algorithm used to calculate the inversion is based on equation (7):
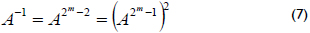
Itoh and Tsujii (Itoh and Tsujii, 1998) proposed a method that reduces the number of multiplications to calculate the inversion, and it is based on the following:
]]>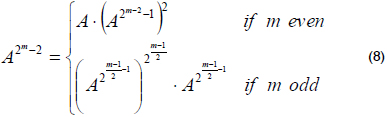
Trace: If A is an element over GF(2m), the trace of A is:
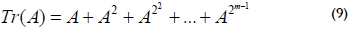
If A = (a0a1a2...am-1)and it is represented in a normal basis, then the trace can be computed efficiently as follows:
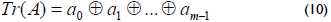
The trace of the element A has two possible values (0 or 1). Quadratic equation solving over GF(2m): If A is an element of GF(2m) represented in a normal basis, then the quadratic equation:
]]>

has 2 - 2T solutions over GF(2m), where T = Tr(A). Therefore, if T = 1, there is no solution, and if T = 0, there are two solutions. If z is one solution, then the other solution is z + 1. For example, if A = 0, the solutions are z = 0 and z = 1 (IEEE std 1363, 2000). The algorithm 1 calculates the quadratic equation over GF(2m) for a normal basis representation.

Square root: Let A = (a0a1a2...am-1) ∈ GF(2m), then
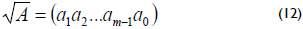
In this case, the square root in a normal basis is a simple rotation of the vector representation (IEEE std 1363, 2000).
Elliptic curve arithmetic
A non-supersingular elliptic curve E(Fq) is defined as a set of points (x, y) ∈ GF(2m)×GF(2m) that satisfies the affine coordinates equation,
]]>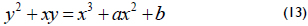
where a and b ∈ Fq and are constants with b ≠ 0 together with the point at infinity denoted by O. The group operations for the elliptic curve arithmetic in affine coordinates are defined as follows. Let P = (x1, y1) and Q = (x2, y2) be two points that belong to the curve, and let the addition inverse of P be defined as -P = (x1, x1 + y1). Then, if Q ≠ -P, the point P + Q = (x3, y3) can be computed as:
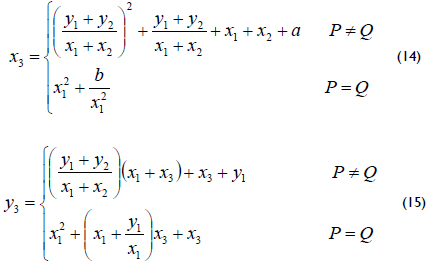
Using the group operations above, the elliptic curve scalar multiplication can be defined as follows. Let E be an elliptic curve over GF(2m), let Q and P ∈ E be two arbitrary elliptic points satisfying equation (13), and let k be an arbitrary positive integer. Then, the elliptic curve scalar multiplication Q = kP is defined as:
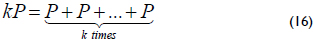
Considering the group operations described in equations (14) and (15) using the finite field arithmetic in affine coordinates, three main elliptic curve operations can be defined: point addition, point doubling and point halving. In the group operations, the inversion is the arithmetic operation that is most expensive over GF(2m), and this operation can be avoided with a projective coordinate representation. In this case, the inversion is avoided by using the finite field multiplication.
A point P in the projective coordinates is represented using three coordinates (X, Y and Z). For the Lopez-Dahab (LD) projective coordinates (Lopez and Dahab, 1999), the projective point (X : Y : Z) with Z ≠ 0 corresponds to the affine coordinates x = X/Z and y = Y/Z2. Then, equation (13) can be mapped from the affine coordinates to the LD projective coordinates as:
]]>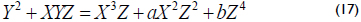
The three group operations for the elliptic curve arithmetic in the projective and affine coordinates can be computed as (Menezes et al., 2003):
1. Point doubling Q = 2P, where Q = (X3 : Y3 : Z3) and P = (X1 : Y1 : Z1) in the projective coordinates, can be performed using 4 finite field multiplications, such as
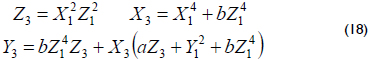
2. Point addition Q + P, where Q = (X1 : Y1 : Z1) in the projective coordinates and P = (x2, y2) in the affine coordinates, can be performed using 8 finite field multiplications, such as
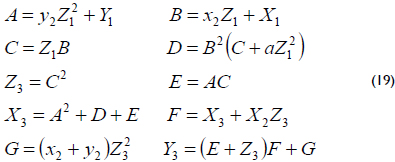
3. Point halving Q/2 is the inverse operation of point doubling. Let P = (x1, y1) and Q = (x2, y2) be the points over the curve (13) in the affine coordinates. The point halving operation is performed by computing P such that Q = 2P by solving the following equations:
]]>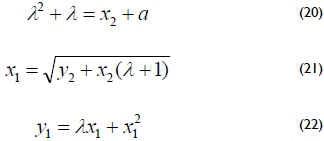
Let the λ-representation of a point Q = (x2, y2) be Q = (x, lQ), where
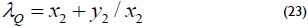
If Q in the λ-representation is the input of the point halving algorithm, then it is possible to compute point halving without using the affine coordinates. In scalar multiplication, repeated point halving operations can be performed directly on the λ-representation. However, when a point addition is required, a conversion to the affine coordinates must be performed. Algorithm 2 computes the point halving operation.

Koblitz Curves
Koblitz curves, or anomalous binary curves, are elliptic curves defined over GF(2m). The main advantage of these curves is that the scalar multiplication operation can be performed without the use of point doubling operations.
]]> An algorithm for scalar multiplication on Koblitz curves is presented by Solinas (Solinas, 2000). The Solinas algorithm or the τ-adic window method computes a special τ-adic expansion of an integer number in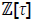 . For example, a special τ-adic expansion is the window τ-adic non-adjacent form (τNAF).
. For example, a special τ-adic expansion is the window τ-adic non-adjacent form (τNAF). The Koblitz curves are curves defined over GF(2m) by:
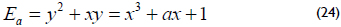
where a ∈ {0,1}, that is, curves E0 and E1.
These curves present the following property: If P(x, y) is a point on the curve Ea, then the point (x2, y2) is also a point on Ea. In addition, they satisfy (x4, y4) + 2(x, y) = µ(x2, y2) for each point (x, y) on Ea, where µ = (-1)1-a. In GF(2m), the Frobenius map τ is an endomorphism that raises every element to its power of two, i.e., τ : x → x2. Then, the Frobenius endomorphism is performed efficiently (cost-free) when the elements of the finite field are represented in a normal basis (Cui and Yang, 2012). Koblitz shows that the point doubling operation can be performed efficiently by using the Frobenius endomorphism, if the binary curve is defined over GF(2m) and a ∈ {0, 1}. Then, the Frobenius map can be defined as τ: (x, y) → (x2, y2). In this case, if the scalar k is represented in τNAF, then
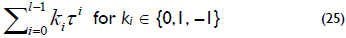
The τ-adic representation can be obtained by repeatedly dividing k by τ, where the remainders of each division step are named digits ui. This procedure is also used to obtain the representation's NAF of the scalar k, namely, k is repeatedly divided by 2. To decrease the number of point additions for the scalar multiplication, it is necessary to obtain a τNAF representation of k that achieves a smaller number of nonzero digits. The scalar multiplication can be computed as:
]]>
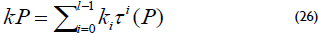
The result corresponds to the Hamming weight of the τNAF, and it is equal to the binary NAF representation, i.e., the Hamming weight ≈ (log2 k)/3, and the length of the τ-adic representation of k is approximately 2m, which is twice the length of the binary NAF representation. However, Solinas presents a method that reduces the length of the τ-adic representation to approximately m. Thus, the Koblitz curves' arithmetic is based on the point addition and Frobenius map τ.
Hardware architectures for elliptic curve cryptoprocessors
In this section, we present the hardware architectures for elliptic curve cryptoprocessors over GF(2163) using a Gaussian normal basis. Each cryptoprocessor is designed using one algorithm for the scalar multiplication, namely, the Lopez-Dahab algorithm (Lopez and Dahab, 1999), the halve-and-add 2-NAF algorithm (Menezes et al., 2000) and the w-τNAF method for Koblitz curves with w = 2, 4, 8 and 16 (Solinas, 2000).
Digit-level multiplier
The finite field multiplication over GF(2m) is an operation that is more important for performing the scalar multiplication. Thus, this operation must be implemented efficiently in hardware. There are several algorithms for performing the finite field multiplication that are presented in Azarderakhsh and Masoleh (2010), Huang et al. (2011,), Wang and Fan (2012) Lee and Chiou (2012).
Azarderakhsh and Masoleh (Azarderakhsh and Masoleh, 2010) proposed a serial or parallel digit-level multiplier with a digit-size d, where 1 ≤ d ≤ m. In this case, if d = m, the multiplier is parallel and if d < m, it is serial and requires 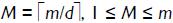 , clock cycles to generate all the m coefficients of C = A·B = (c0c1c2...cm-1), where A = (a0a1a2...am-1)and B = (b0b1b2...bm-1)are elements represented in a GNB over GF(2m). Figure 1 shows the digit-level GF(2m) multiplier for T = 4, where A, B and C are registers for storing the input and output elements.
, clock cycles to generate all the m coefficients of C = A·B = (c0c1c2...cm-1), where A = (a0a1a2...am-1)and B = (b0b1b2...bm-1)are elements represented in a GNB over GF(2m). Figure 1 shows the digit-level GF(2m) multiplier for T = 4, where A, B and C are registers for storing the input and output elements.
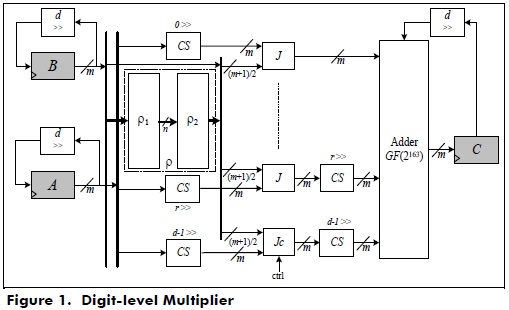
The block ρ is formed by the blocks ρ1 and ρ2, and its structure depends on type T of the GBN with T ≥ 2 and the multiplication matrix R. The block J is a set of m, two-input AND gates. The block CS is a d-fold cyclic shift and an adder GF (2163), which is a set of two-input XOR gates.
]]> The block ρ1 is an optimal set of XOR gates that are obtained using (27), and ρ2 is a set of XOR gates that are obtained from the main matrix ρ:
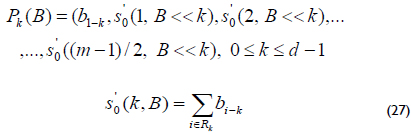
The time complexity of the digit-level multiplier is TA + (2 + 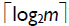 )TX, where TX and TA are the delay time of a two-input XOR gate and a two-input AND gate, respectively. The area complexity of this multiplier is m2 ANDs and ≤ 2m2 - 2m XORs (Azarderakhsh and Masoleh, 2010).
)TX, where TX and TA are the delay time of a two-input XOR gate and a two-input AND gate, respectively. The area complexity of this multiplier is m2 ANDs and ≤ 2m2 - 2m XORs (Azarderakhsh and Masoleh, 2010).
To implement the digit-level multiplier with a digit-size d = 55 in hardware, that is M = 3 clock cycles, a Matlab code is written to generate the equations of the blocks ρ1 and ρ2, which are synthesized using VHDL.
Hardware architecture using the Lopez-Dahab algorithm
The scalar multiplication kP for non-supersingular elliptic curves over binary fields using the Lopez-Dahab algorithm is shown in Algorithm 3, which is a modified version of the Montgomery algorithm, where the same operations are performed during each iteration of the main loop (D. Hankerson et al., 2003).

In this case, the scalar multiplication is performed in three steps: 1) conversion of P from affine to projective coordinates; 2) compute Q = kP by addition and doubling; and 3) conversion of Q from projective to affine coordinates.
]]> To implement the above algorithm in hardware, we initially define three functions: Madd() performs the point addition, Mdouble() performs the point doubling and Mxy() performs the conversion from projective to affine coordinates. These functions are defined as follows:
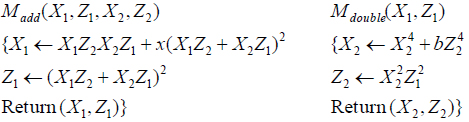
where, (x, y) and (x3, y3) are the coordinates of points P and Q = kP, respectively.
Point addition and point doubling are implemented in hardware using the data dependence graph shown in Figure 2, and the conversion from the projective to affine coordinates is implemented using two digit-level multipliers for the data dependence graph shown in Figure 3. The inversion operation is implemented using the Itoh-Tsujii algorithm (Itoh and Tsujii, 1998).
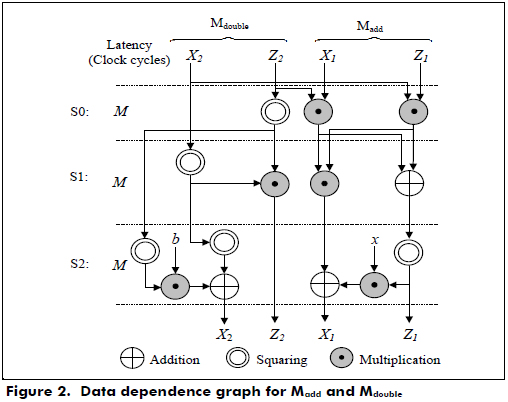
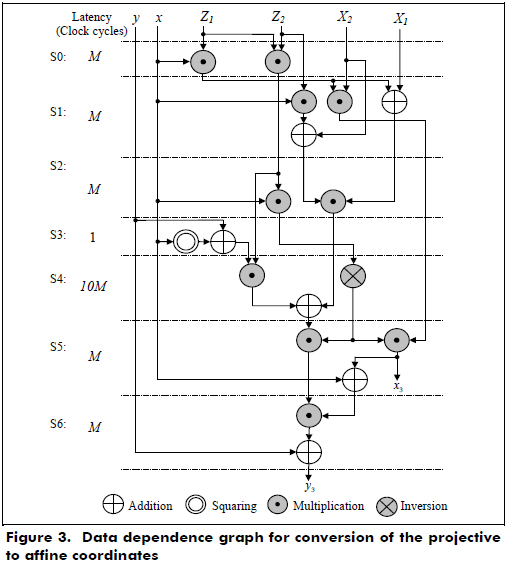
According to Figures 2 and 3, the latencies for Madd and Mdouble and the projective to affine conversion are 3M and 15M +1, respectively, where M is the latency for a finite field multiplication.
]]> In step 4 of Figure 3, two multipliers are used, and one of them with the block of rotation performs the inversion of an element A ∈ GF(2163). In this case, the latency of the inversion is 10M because it needs 10 finite field multiplications for m = 163. In step 6, a multiplier is only used because the last operation of the coordinate conversion requires a multiplication.The architecture of the cryptoprocessor over GF(2163) using the Lopez-Dahab algorithm is shown in Figure 4. It uses two register files, two parallel digit-level multipliers, one inversion block, several squaring and adder blocks, a main control and an FSM to perform the point addition, point double and conversion from the projective to affine coordinates.
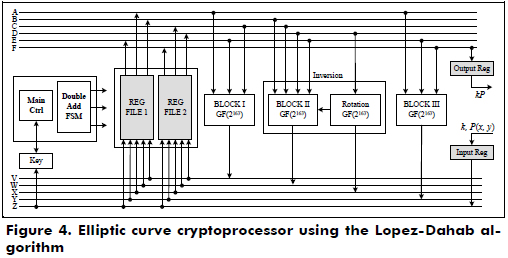
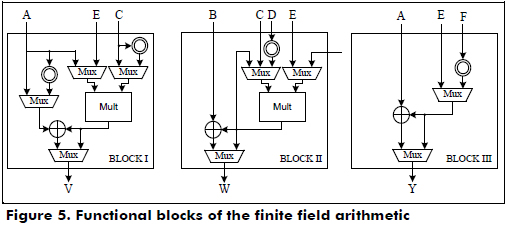
The functional blocks that perform the finite field arithmetic operations over GF(2163) for the Lopez-Dahab cryptoprocessor are shown in Figure 5. It is important to mention that the performance of any cryptoprocessor depends on the efficient implementation of the hardware for the finite field arithmetic.
The main control is an FSM that generates the control signals to perform the scalar multiplication, process the key, initialize the cryptoprocessor and control the I/O registers. The second FSM performs the point addition, point doubling and conversion from the projective to the affine coordinates.
In Figure 6, the ASM chart of the main control is shown, where the variables X1, Z1, X2 and Z2 are initialized and stored in the register files. Each bit of the scalar k is evaluated from left to right to perform the operations Madd and Mdouble using the data dependence graph shown in Figure 2. If the bit ki is '1', then Madd(X1,Z1,X2,Z2), Mdouble(X2,Z2) are computed. Else, Madd(X2,Z2,X1,Z1), Mdouble(X1,Z1). When all bits of the scalar k are evaluated, the conversion from the projective to affine coordinates is executed using the data dependence graph shown in Figure 3, and kP in the affine coordinates is stored in the output register.
]]>
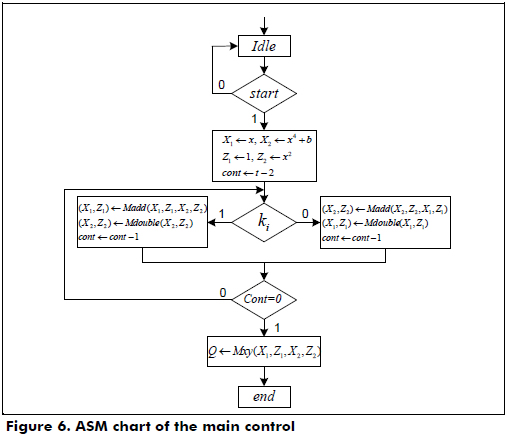
Algorithm 3 is more resistant against simple power analysis and timing attacks. This is because the computation cost does not depend on the specific bit of the scalar k. For each bit of the scalar k, one point addition and one point doubling are performed. The proposed scheme has two different execution paths depending on the current bit of the scalar k. Both execution paths have the same complexity and require the same number of clock cycles.
Hardware architecture using the halve-and-add algorithm
Schroeppel (Schroeppel, 2000) and Knudsen (Knudsen, 1999) independently proposed the halve-and-add algorithm to accelerate the scalar multiplication on the elliptic curves defined over the binary extension fields. This algorithm uses an elliptic curve primitive called point halving as shown in algorithm 2.
Because, theoretically, the point halving operation is three times faster than the point doubling operation, it is possible to accelerate the scalar multiplication Q = kP by replacing the double-and-add algorithm with the halve-and-add algorithm, which uses an expansion of the scalar k in terms of negative powers of 2 (Mercurio et al., 2006).
In the halve-and-add algorithm, it is necessary to transform the integer k = (km-1,...,k0)2. If k´ is defined by
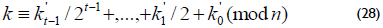
where n represents the order of the base point P, then
]]>

Equation (29) can be generalized to a window-NAF. The NAFw of a positive integer k and w ≥ 2 is represented by the expression 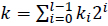 , where each nonzero coefficient ki is odd and at most, one of any w consecutive digits is nonzero. In this case, the NAFw of k can be computed using algorithm 4.
, where each nonzero coefficient ki is odd and at most, one of any w consecutive digits is nonzero. In this case, the NAFw of k can be computed using algorithm 4.

In this work, a Maple code is written to obtain the expansion coefficients NAFw with w = 2, namely, the coefficients NAFw(2τ-1 k mod n), which are represented by 2-bits.
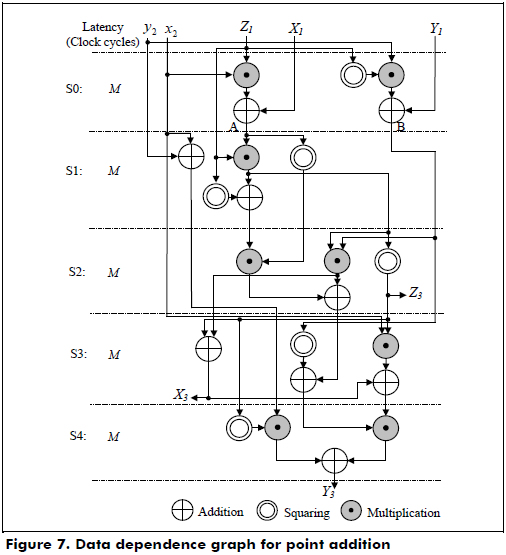
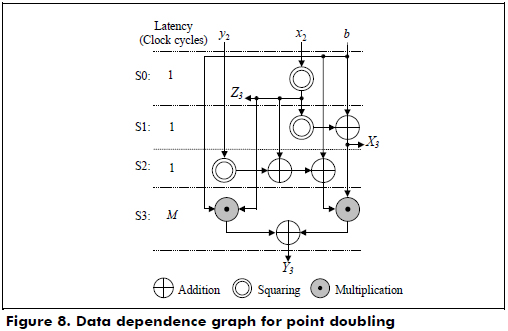
The halve-and-add algorithm is shown in algorithm 5. Step 3 of the algorithm performs the point addition Qi + P in the Lopez-Dahab mixed coordinates(Qi and P are represented in LD projective and affine coordinates, respectively) using equation (14) and the halving point P/2 in the affine coordinates or λ-representation, if bit ki´ ≠ 0; else, compute point halving. In this case, it is important to mention that if the results of the first two operations A and B of equation (19) are equal to zero, the point doubling 2P is performed in the LD projective coordinates using equation (18) with X1 = x2, Y1 = y2 and Z1 = 1.

The point addition in the LD mixed coordinates and the point doubling in the LD projective coordinates are implemented in hardware using the data dependence graphs shown in Figure 7 and Figure 8, respectively. According to Figures 7 and 8, the latencies for the point addition and point doubling are 5M and M + 3, respectively.
]]>
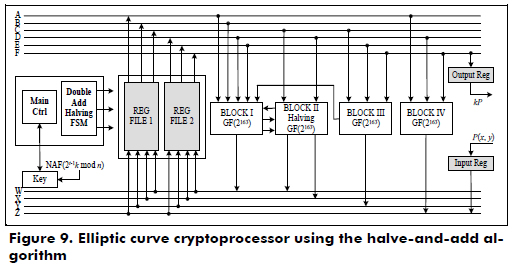
The architecture of the cryptoprocessor over GF(2163) using the halve-and-add algorithm is shown in Figure 9, and it uses two register files, two digit-level finite multipliers, one solving quadratic equation block, one point halving block, several squaring and adder blocks, a main control and an FSM to perform the point addition, point doubling and point halving.
The functional blocks that perform the finite field arithmetic operations over GF(2163) for the halve-and-add cryptoprocessor are shown in Figure 10. In this case, finite field arithmetic operations are the addition, squarer, square root, trace, half trace (quadratic equation solving in a normal basis) and multiplication.
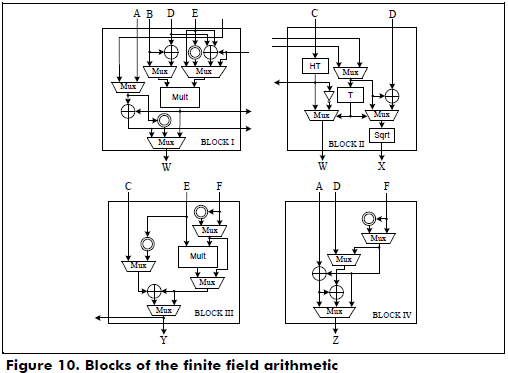
The main control is an FSM that generates the control signals to perform the scalar multiplication, process the key, initialize the cryptoprocessor and control the I/O registers. The second FSM performs the point addition, point doubling and point halving.
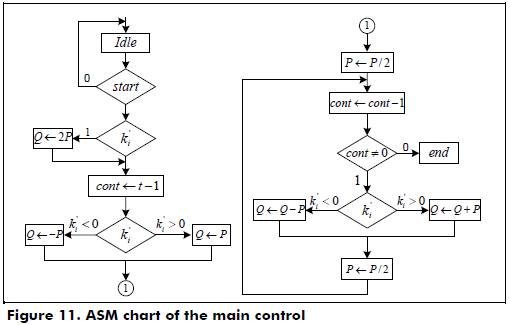
]]> In Figure 11, the ASM chart of the main control is shown, where the sequence processing is as follows: initialize coordinate Q according to the sign of the bit k't-1; perform the point halving operation on P; evaluate the bit k'i for i > t-1; compute the point addition in the LD mixed coordinates and point halving on P if k'i ≠ 0, else compute point halving; and perform the conversion of the point P in the λ-representation to the affine coordinates only when a point addition is required. Finally, Q = kP is obtained in the LD projective coordinates.
Algorithm 7 performs the rounding of a complex number λ0 + λ1τ with λ0 and λ1 ∈  to obtain an element
to obtain an element  .
.
Hardware architecture using the w-τNAF algorithm
The length of the τ-adic representation for 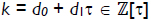 is roughly twice log2(max(d0, d1)). Solinas (Solinas, 2000) presents a method that reduces the length of the τ-adic representation. The objective is to find
is roughly twice log2(max(d0, d1)). Solinas (Solinas, 2000) presents a method that reduces the length of the τ-adic representation. The objective is to find 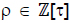 of small norm with ρ ≡ k (mod δ), where δ = (τm - 1)/(τ - 1), and use τNAF(ρ) to calculate ρP.
of small norm with ρ ≡ k (mod δ), where δ = (τm - 1)/(τ - 1), and use τNAF(ρ) to calculate ρP.
Algorithm 6 calculates an element ρ' ≡ k (mod δ), which is also written as ρ' ≡ k partmod δ. Solinas proved that l(ρ) ≤ m + a and if C ≥ 2, then l(ρ´) ≤ m + a + 3.


where ui ∈ {0, ±α1, ±α3,..., ±α2w-1-1}, ul-1 ≠ 0 and at most, one of any w consecutive digits is nonzero. Then, kP = αu0P + ταu1P + ... + τl-1αl-1P, when the scalar k is represented in w-τNAF.
The w-τNAF expansion can be efficiently computed using algorithm 8, which can be viewed as an approach similar to the general NAF algorithm. In this work, a Maple code is written to obtain the expansion w-τNAF of the scalar k with w = 2, 4 and 8, generating 8-bit expansion coefficients and w = 16, generating 16-bit expansion coefficients.

Solinas proposed algorithms to compute kP using the window τNAF method for the scalar k, namely, kP is calculated using the w-τNAF method and Horner's rule (Solinas, 2000). An efficient scalar multiplication algorithm that uses the w-τNAF method is presented in algorithm 9, where step 1 calculates the w-τNAF of the scalar k with the partial reduction modulo δ = (τm - 1)/(τ - 1), namely, w-τNAF(ρ ≡ k mod (δ)), where ρ ≡ k mod (δ) is obtained from algorithms 6 and 7; step 2 generates the multiples of the point P and step 4.2 performs the point addition Q + Pu, when the bit ui ≠ 0, and point doubling 2Q, when the results of the two first operations A and B of equation (19) are equal to zero.

The architecture of the cryptoprocessor over GF(2163) using the w-τNAF algorithm for Koblitz curves is shown in Figure 12, and it uses two register files, two digit-level finite multipliers, one Frobenius map block, one RAM that stores the expansion coefficients w-τNAF of the scalar k, two ROMs that store the pre-computed points Pu in the affine coordinates, which were obtained from Matlab for w = 2, 4, 8 and 16, several squaring and adder blocks, a main control and an FSM to perform the point addition, point doubling and tQ.
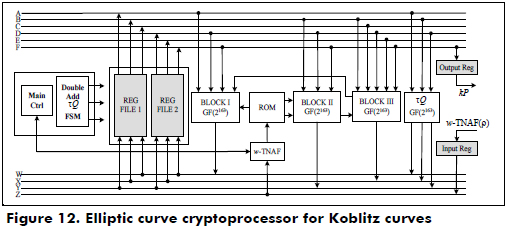
The functional blocks that perform the finite field arithmetic operations over GF(2163) for the w-τNAF cryptoprocessor for Koblitz curves are shown in Figure 13.
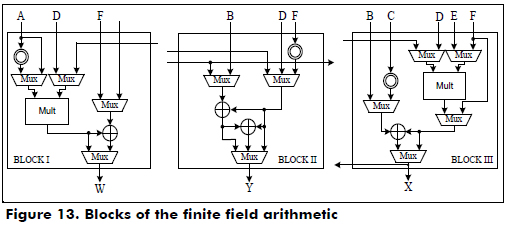
The main control is an FSM that generates the control signals to perform the scalar multiplication, process the key, initialize the cryptoprocessor and control the I/O registers. The second FSM performs the point addition, point doubling and tQ.
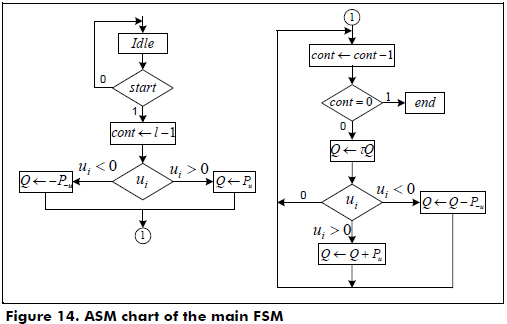
In Figure 14, the ASM chart of the main control is shown, where the sequence processing is as follows: initialize the Q coordinate according to the sign of the bit ui of the w-τNAF expansion; evaluate the bits ui for i > τ-1; and compute the point addition in the LD mixed coordinates and the Frobenius map τ on Q, if ui ≠ 0. Else, compute tQ. Finally, Q = kP is obtained in the LD projective coordinates. In Figure 14, the ASM of the FSM is shown. One important remark is that the Koblitz curves are resistant to simple power analysis and to all the known special attacks (T. Juhas, 2007).
]]>
Hardware verification and synthesis results
The López-Dahab, halve-and-add and w-τNAF cryptoprocessors are described using generic structural VHDL, are synthesized for a digit-size of d = 55 on the Stratix-IV FPGA (EP4SGX180HF35C2) using the Altera Quartus II version 12 design software for the implementation and are verified using SignalTap II and Matlab.
Hardware verification of the cryptoprocessors
To verify the synthesis and simulation results of the cryptoprocessors, the following parameters for a pseudo-random elliptic curve are used according to the National Institute of Standards and Technology (NIST, 2000):
1. Random elliptic curves B-163:
The form of the curve is: y2 + xy = x3 + x + b
Gx = 3F0EBA16286A2D57EA0991168D4994637E8343E36
Gy = 0D51FBC6C71A0094FA2CDD545B11C5C0C7973244F1
b = 20A601907B8C953CA1481EB10512F78744A3205FD
]]>


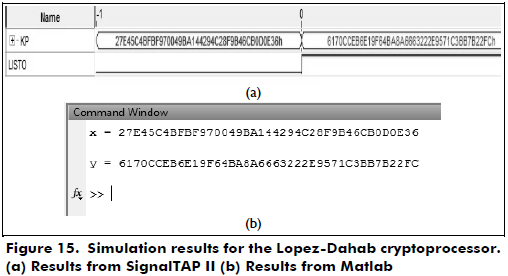
From Figures 15 through 17, we can see that the results obtained from Matlab are the same as the results from SignalTAP II. Then, the hardware results verify the correct functionality of the designed cryptoprocessors.
Synthesis results for the cryptoprocessors
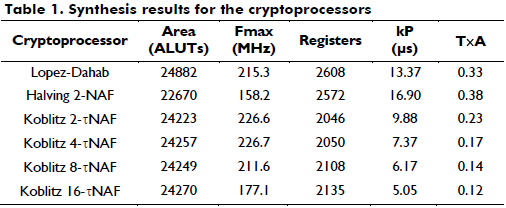
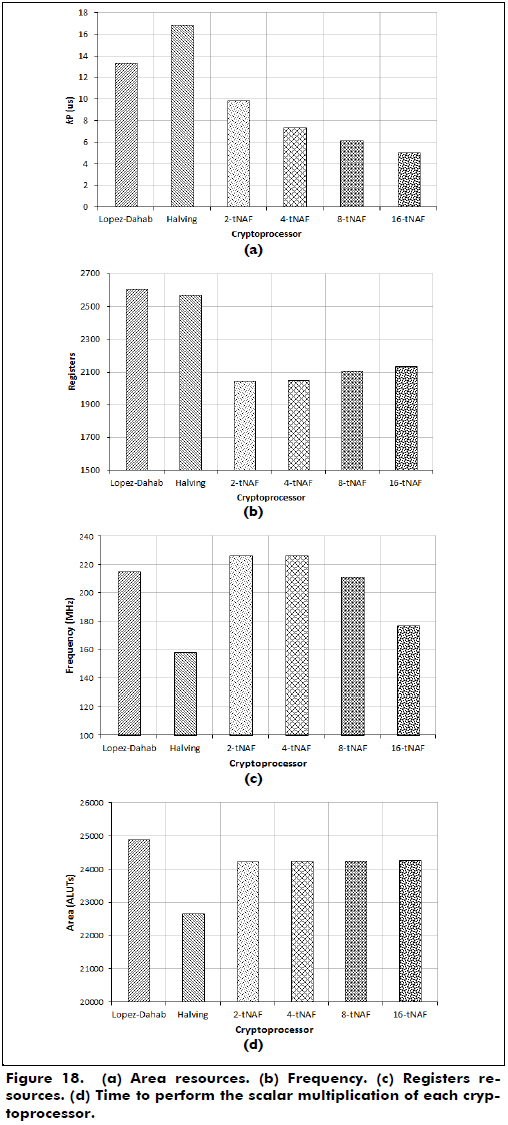
The synthesis results of the cryptoprocessors over GF(2163) are shown in Table 1. Additionally, some of the data presented in Table I are plotted in Figure 18.
Comparison of the results with other works
To compare the performance of the designed cryptoprocessors with respect to the cryptoprocessors presented in the literature, Table 2 shows several design parameters and processing times, such as area resources, frequency, kP time and time-area product. However, it is important to mention that performing a fair comparison in hardware design is very difficult because there are other technical considerations, including the technologies, hardware platforms, software tools, scalar multiplication algorithms, finite field representations, and size of the fields.
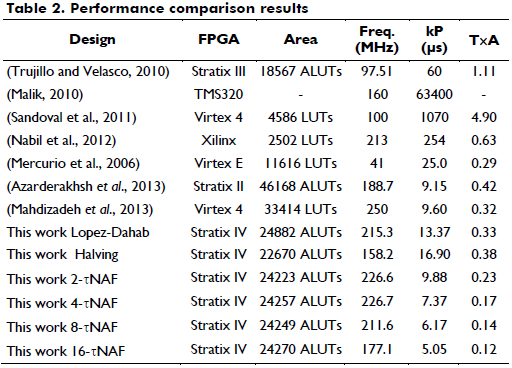
From Table 2, it is possible to observe that the GF(2163) cryptoprocessor presented in Mahadizadeh et al (2013) requires less time to perform the scalar multiplication than our processor based on the Lopez-Dahab algorithm because the first processor uses three digit-level multipliers, and our design uses two digit-level multipliers, and the latency to compute Madd and Mdouble is 3M. However, the first processor requires more area than our processor. Mercurio et al (2006) computes kP by using the half-and-add algorithm, m=163, polynomial bases representation and one parallel multiplier. Our processor requires more area than the mentioned processor because it uses two digit-level multipliers, but our design requires less time to perform the scalar multiplication, and the latency to compute the point addition is 5M. Finally, our processor is based on the Koblitz curves and has a higher performance (area and time) than the processor presented in Azarderakhsh (2013) because our design has a latency of 5M to compute the point addition, and it uses two digit-level multipliers and a window method that allows us to reduce the amount of point addition operations.
From Table 2, it is possible to observe that the GF(2163) cryptoprocessor presented in Mahadizadeh et al (2013) requires less time to perform the scalar multiplication than our processor based on the Lopez-Dahab algorithm because the first processor uses three digit-level multipliers, and our design uses two digit-level multipliers, and the latency to compute Madd and Mdouble is 3M. However, the first processor requires more area than our processor. Mercurio et al (2006) computes kP by using the half-and-add algorithm, m=163, polynomial bases representation and one parallel multiplier. Our processor requires more area than the mentioned processor because it uses two digit-level multipliers, but our design requires less time to perform the scalar multiplication, and the latency to compute the point addition is 5M. Finally, our processor is based on the Koblitz curves and has a higher performance (area and time) than the processor presented in Azarderakhsh (2013) because our design has a latency of 5M to compute the point addition, and it uses two digit-level multipliers and a window method that allows us to reduce the amount of point addition operations.
Conclusions
This work presents the design of elliptic curve cryptoprocessors to compute the scalar multiplication over GF(2163) using the GNB. The Lopez-Dahab, halve-and-add and w?τNAF algorithms are used to design the cryptoprocessors, which are described using generic structural VHDL, synthesized on the Stratix IV FPGA (EP4SGX180HF35C2).
Considering the hardware verification results, the 16-τNAF cryptoprocessor performs the scalar multiplication in less time (5.05 ms), and the 2-NAF halve-and-add cryptoprocessor uses fewer area resources than the other processors, in this case, 22670 ALUTs. All the cryptoprocessors use roughly 17% of the ALUTs of the FPGA.
]]> Additionally, it is important to mention that the algorithms are synthetized on the same hardware platform using Quartus II, are simulated in Modelsim, and are verified using SignalTAP and Matlab; the cryptoprocessors use two digit-level finite field multipliers over GF(2163) in the GNB; the expansion coefficients for the private key k are obtained using the software Maple; and the FSMs use a data dependence graph to perform kP to achieve the minimal states.Future work will be oriented to increase the performance of the designed cryptoprocessors and the hardware implementation of the GF(2233) processors. Additionally, new cryptoprocessors will be designed based on elliptic curves that are not included in the National Institute of Standards and Technology (NIST), such as the Hessian and Edwards curves that perform the scalar multiplication kP.
References
Amara, M., & Siad, A. (2011). Hardware implementation of arithmetic for elliptic curve cryptosystems over GF(2^m). In World Congress on Internet Security (WorldCIS) (pp. 73-78). London: IEEE. [ Links ]
Azarderakhsh, R., & Masoleh, R. (2010). A Modified Low Complexity Digit-Level Gaussian Normal Basis Multiplier. Arithmetic of Finite Fields (pp. 25-40). Turkey: Springer. [ Links ]
Azarderakhsh, R., & Masoleh, R. (2013). High-performance implementation of point multiplication on Koblitz Curves. IEEE Transactions on Circuits and Systems, 60(1), 41 - 45. [ Links ]
Chester, R., & Mukhopadhyay, D. (2008). Progress in Cryptology - INDOCRYPT 2008. Kharagpur: Springer. [ Links ]
Cui, X.-N., & Yang, J. (2012). An FPGA based processor for Elliptic Curve Cryptography. In International Conference on Computer Science and Information Processing (CSIP) (pp. 343-349). Shaanxi: IEEE. [ Links ]
Ghanmy, N., Khlif, N., Fourati, L., & Kamoun, L. (2012). Hardware implementation of elliptic curve digital signature algorithm ECDSA on Koblitz curves. In International Symposium on Communication Systems, Networks & Digital Signal Processing (CSNDSP) (pp. 1 - 6). Poznan: IEEE. [ Links ]
Hankerson, D., Menezes, A., & Vanstone, S. (2004). Guide to Elliptic Curve Cryptography. Springer. [ Links ]
Huang, T., Chang, C., Chiou, C., & Tan, S. (2011). Non-XOR approach for low-cost bit-parallel polynomial basis multiplier over GF(2^m). Information Security, IET, 5(3) 152-162. [ Links ]
IEEE std 1363. (2000). 1363-2000 IEEE Standard Specifications for Public-Key Cryptography. IEEE Computer Society. [ Links ]
Itoh, T., & Tsujii, S. (1988). A fast algorithm for computing multiplicative inverses in GF(2^m) using normal bases. Information and Computation, 78(3), 171-177. [ Links ]
Jeevananthan, S., & Muthukumar, B. (2010). High speed hardware implementation of an elliptic curve cryptography (ECC) co-processor. In Trendz in Information Sciences & Computing (TISC) (pp. 176-180). Chennai: IEEE. [ Links ]
Johnson, D., Menezes, A., & Vastone, S. (2001). The Elliptic Curve Digital Signature Algorithm (ECDSA). International Journal of Information Security, 1(1), 36-63. [ Links ]
Juhas, T. (2007). The Use of Elliptic Curves in Cryptography. Retrieved from: http://munin.uit.no/bitstream/handle/10037/1091/thesis.pdf?sequence=5 [ Links ]
Knudsen, W. (1999). Elliptic Scalar Multiplication Using Point Halving. Advances in Cryptology - ASIACRYPT (pp. 135-149). Berlin: Springer. [ Links ]
]]>Koblitz, N. (1987). Elliptic curve cryptosystems. Mathematics of computation, 48(1987), 203-209. [ Links ]
Lai, J.-Y., Hung, T.-Y., Yang, K.-H., & Huang, C.-T. (2010). Proceedings of IEEE International Symposium on Circuits and Systems (ISCAS) (pp. 3933 - 3936). Paris: IEEE. [ Links ]
Lee, C., & Chiou, C. (2012). Scalable Gaussian Normal Basis Multipliers over GF(2^m) Using Hankel Matrix-Vector Representation. Journal of Signal Processing Systems, 69(2), 197-211. [ Links ]
Lopez, J., & Dahab, R. (1999). Fast Multiplication on Elliptic Curves Over GF(2^m) without precomputation. Cryptographic Hardware and Embedded Systems, 1717, 316-327. [ Links ]
Mahdizadeh, H., & Masoumi, M. (2013). Novel Architecture for efficient FPGA implementation of elliptic curve cryptographic processor over GF(2^163). IEEE transactions on very large scale integration (VLSI) systems, 21(12), 1-4. [ Links ]
]]>Malik, M. (2010). Efficient implementation of Elliptic Curve Cryptography using low-power Digital Signal Processor. In International Conference on Advanced Communication Technology (ICACT) (pp. 1464-1468). Phoenix Park: IEEE. [ Links ]
Masoleh, R. (2006). Efficient algorithms and architectures for field multiplication using Gaussian normal basis. IEEE Transactions on Computers, 55(1), 34-47. [ Links ]
Mercurio, S., & Rodriguez, F. (2006). Elliptic Curve Scalar Multiplication using Point Halving on Reconfigurable Hardware Platforms (pp. 1-5). Mexico: CiteSeerX. [ Links ]
Miller, V. (1986). Advances in Cryptology. In CRYPTO '85 Proceedings. Santa Barbara: Springer. [ Links ]
Morales, S., Uribe, F., & Badillo, A. (2011). A reconfigurable GF(2^m) elliptic curve cryptographic coprocessor. In Southern Conference on Programmable Logic (SPL) (pp. 209 - 214). Cordoba: IEEE. [ Links ]
]]>NIST. (2013). Digital Signature Standard. Gaithersburg: Federal Information Processing Standards. [ Links ]
Rahuman, A., & Athisha, G. (2010). Reconfigurable architecture for elliptic curve cryptography. In International Conference on Communication and Computational Intelligence (INCOCCI) (pp. 461-466). Erode: IEEE. [ Links ]
Schroeppel, R. (2000). United States Patent No. EP1232602. [ Links ]
Solinas, J. (2000). Efficient Arithmetic on Koblitz Curves. Designs, Codes and Cryptography, 19(2-3), 195-249. [ Links ]
Trujillo, V., & Velasco, J. (2010). Hardware Architectures for Elliptic Curve Cryptoprocessors Using Polynomial and Gaussian Normal Basis over GF(2^233). Lecture Notes in Computer Science, 6480, 79-103. [ Links ]
]]>Wang, Z., & Fan, S. (2012). Efficient Montgomery-Based Semi-Systolic Multiplier for Even-Type GNB of GF(2^m). IEEE Transactions on Computers, 61(3), 415-419. [ Links ]
]]>