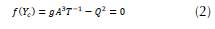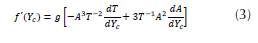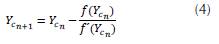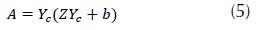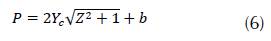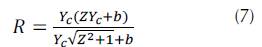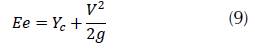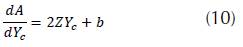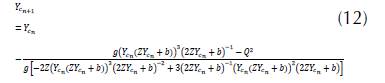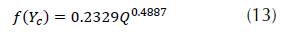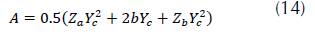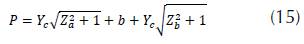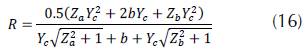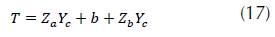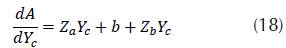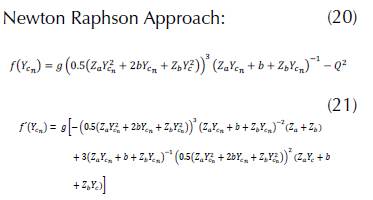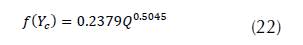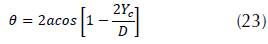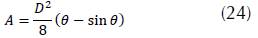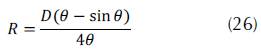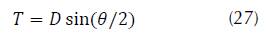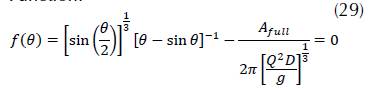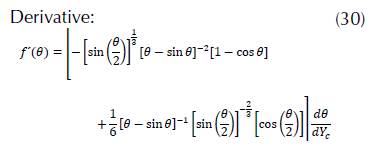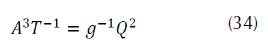English (pdf)
Article in xml format
Article references
Automatic translation
Send this article by e-mail
Cited by SciELO 
Cited by Google 
Similars in
SciELO 
Similars in Google 
Permalink
INTRODUCTION
Teaching and learning ways must be in line with technological developments that are experienced today (Contreras, Escobar, & Tristancho, 2013;Sotelo & Solarte,2014).The generation of different learning scenarios leads the student to relate the influence of diverse variables and methodologies in real problems solution (Gómez, Galvis, & Mariño, 1998). In this sense, applications development for smartphones, becomes an attractive alternative (Gasca, Camargo, & Medina, 2014), when they are oriented to educational processes (Jonoski et al., 2012). Educational software (ES), are defined as applications or computer programs that facilitate the teaching-learning process (Vidal, Gómez, & Ruiz, 2010; Drumea, 2012). In the free-flowing hydraulic field, most equations that describe the flow behavior do not resist an analytical development, due mainly, to the non-linearity of the functions. Which requires numerical methods implementation that solve the hydraulic problem iteratively (Diaz & Benitez, 1998). In real flow problems it is necessary to use successive approximation methods (Vidal, Gómez, & Ruiz, 2010). The developed algorithm calculates the critical depth from the numerical method of Newton-Raphson, for 5 successive iterations, based on a preset seed value, which accelerates the convergence.
Critical Flow
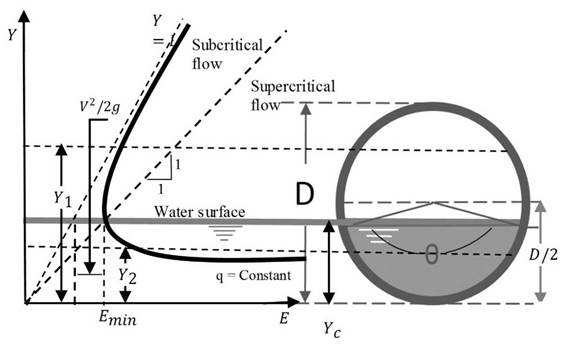
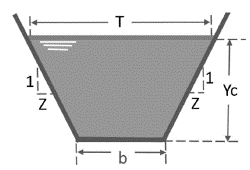
The Froude Number relates the speed, the geometric parameters of the section and the gravitational effects. The critical depth of the flow is defined as the condition for which, the Froude Number (FN) is equal to 1, where the specific energy is minimal (equation 1). If FN < 1, a subcritical flow is established, and if NF > 1, the flow is supercritical (Figure 1).
Froude:
Where: V = Speed (m/s); A = Hydraulic area (m2); T = Mirror (m); g = Gravity (m/s2).
Function:
Where: Q = Flow (m3/s); A = Hydraulic area (m2); T = Mirror (m); g = Gravity (m/s2).
Derivative:
Newton Raphson Approach:
METHODOLOGY
For the application development we used iterative and incremental processes (Agile Development), in three specific phases:
In the first phase, the flow diagram of the iterative process for each of the hydraulic sections (rectangular, trapezoidal, trapezoidal asymmetric, triangular, triangular asymmetric, parabolic and circular) was established.
In the second phase, the source code (JavaScript) was developed (Lindley, 2013).
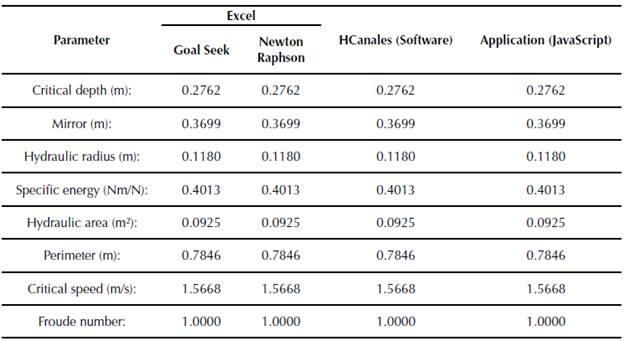
For the last phase, the application was validated by comparing the results against the values obtained by Excel analysis tool (Goal Seek) and by Hcanales® software.
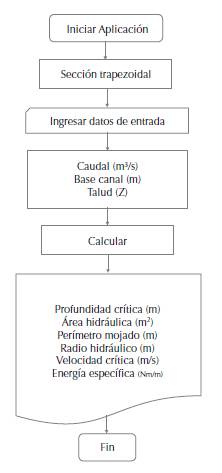
The flow chart for the user interface is presented below, which varies according to the selected hydraulic section (Figure 2).
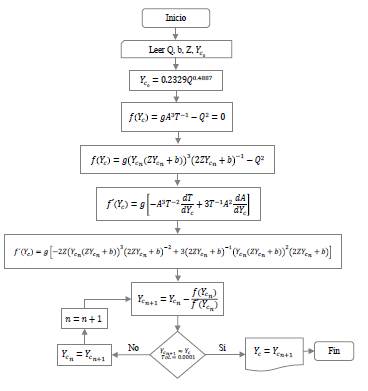
The algorithm shown in Figure 3, was used to program the solution for trapezoidal channel.
In case of a circular section, the height of critical depth exceeds the diameter value, the application generates a warning, where it is recommended to increase the diameter.
RESULTS
Trapezoidal Channel
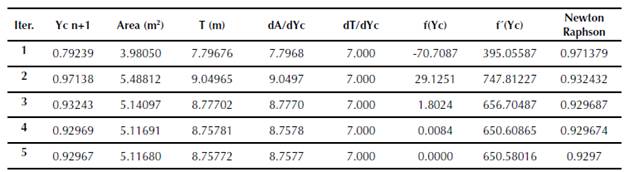
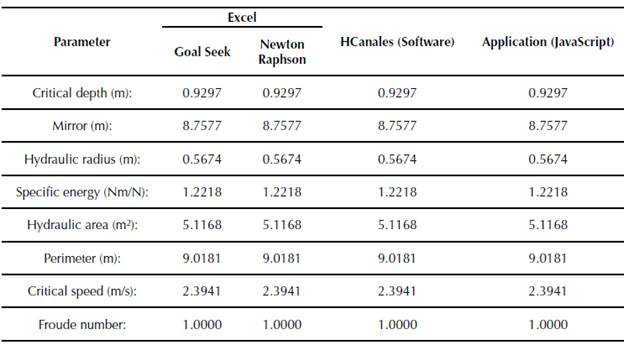
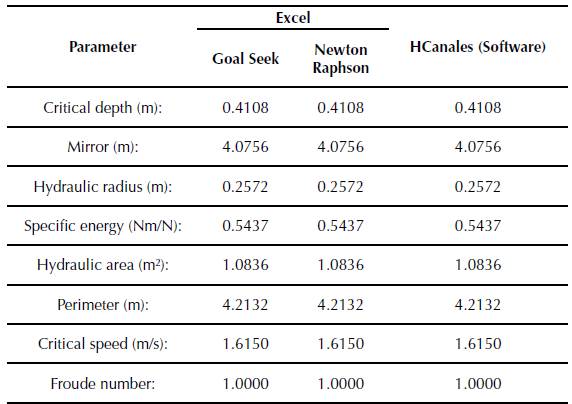
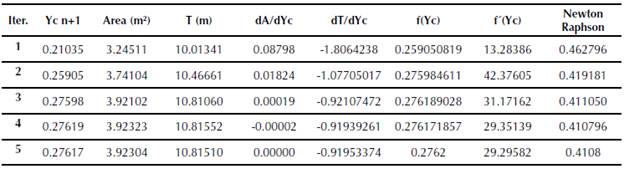
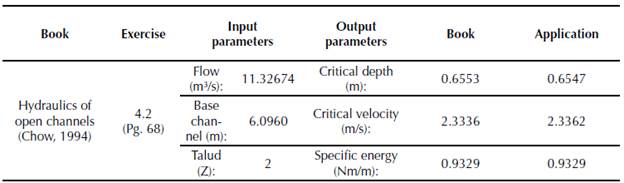
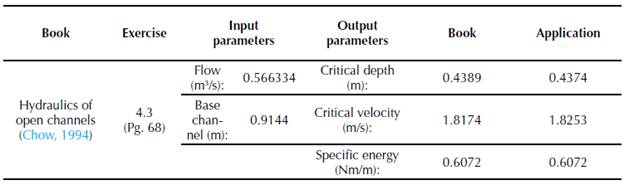
When you start the application, a menu with seven options of hydraulic sections is displayed (rectangular, trapezoidal, asymmetric trapezoidal, triangular, asymmetric triangular, parabolic and circular). For each section, the algorithm calculates: critical depth, mirror, hydraulic radius, specific energy, flow type, hydraulic area, wet perimeter, critical flow velocity and the Froude number. In order to validate the application, it is proposed to determine the critical depth for a symmetric trapezoidal channel (figure 5), by means of three different methodologies: Newton Raphson, Goal Seek (Excel) and Hcanales®. Hydraulic channel conditions are in Table 1.
Hydraulic area:
Wet perimeter:
Hydraulic radius:
Mirror:
Specific Energy:
Considering (1), (2) and (3), we obtain:
Derivative hydraulic area:
Mirror derivative:
Approach Newton Raphson:
In the case of symmetric trapezoidal channel, the following function is proposed for seed value:
Where: Q = Flow rate (m³/ s); Y_c = Critical depth (m).
The results obtained from these three methodologies, generate the same value for the critical depth, under the initial conditions established.
Asymmetric Trapezoidal Channel
Considering (1), and with the purpose of verifying the capacity of the application for critical depth calculation, we proposed an asymmetric trapezoidal section, with these hydraulic conditions:
Hydraulic area:
Wet perimeter:
Hydraulic radius:
Mirror:
Hydraulic area derivative:
Mirror derivative:
From equations (2), (3) and (4), we can conclude that:
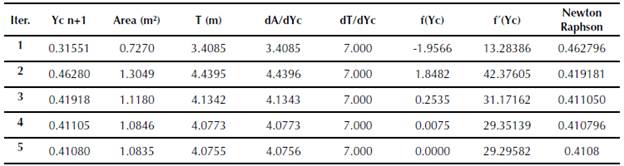
For the asymmetric trapezoidal channel, a potential function was implemented: critical depth vs. flow, for the initial value (seed value). This function accelerates the numerical method convergence. The visual code used in Excel is shown in Figure 9.
Table 5 Critical depth calculation (Excel, Newton-Raphson) (Asymmetric trapezoidal channel)
Source: Authors.
Fuente: Authors.
Figure 9 Visual code (Excel). Iteration for Yc calculation. (Asymmetric trapezoidal channel)
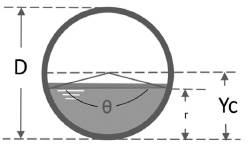
Circular Channel
To evaluate the Application results, we present the following hydraulic problem:
Central Angle
Hydraulic area:
Wet perimeter:
Hydraulic radius:
Mirror:
Hydraulic area derivative:
Newton Raphson Approach:
Where:
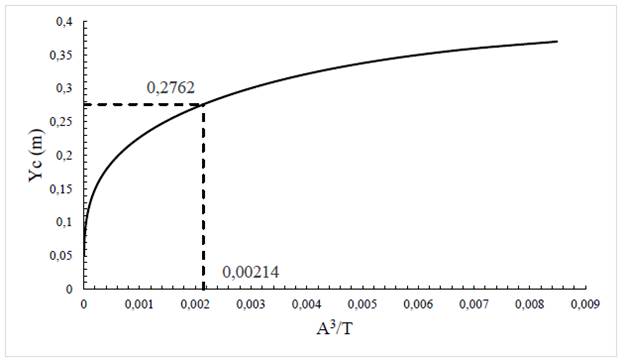
Figure 13. was constructed from the section factor for critical flow.
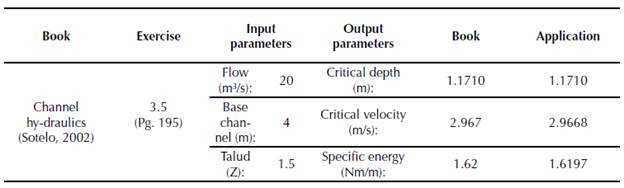
Finally, the application was submitted to some exercises development proposed in different Hydraulics books. In order to validate the algorithm developed, the results are presented in tables 10, 11 and 12. Similarly, the results calculated by the Application are shown in figures 15, 16 and 17.
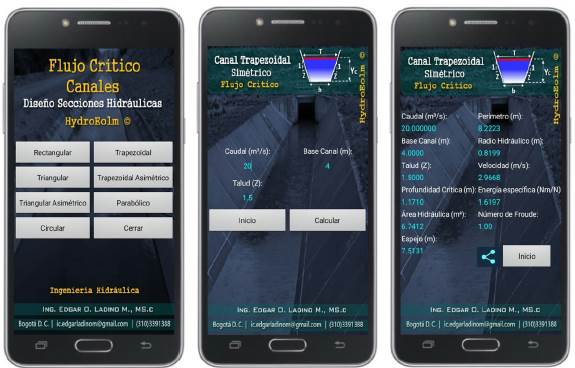
Source: Authors.
Figure 15 Exercise 3.5, Hydraulics of channels, Gilberto Sotelo (Application Critical depth calculation)
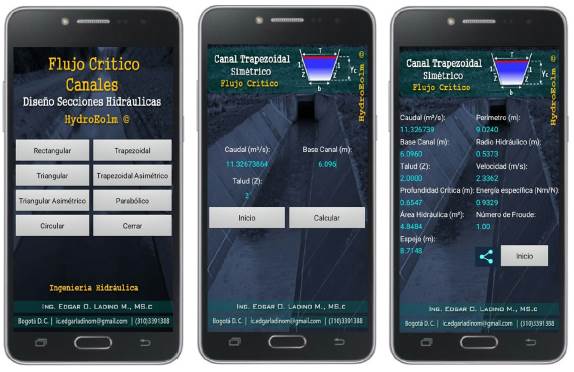
Source: Authors.
Figure 16 Exercise 4.2, Hydraulics of open channels, Ven Te Chow (Application Critical depth calculation)
CONCLUSIONS
The algorithm developed for the application "Diseño de Canales Hidráulicos HydroEolm" under JavaScript programming language avoids the use of calculation curves for critical depth. The results showed that the application effectively calculates the critical depth, critical speed, hydraulic area, specific energy, wet perimeter and the mirror.
In the application development, the results were compared with different exercises proposed in Hydraulics books, showing optimal outputs. Likewise, about 95 hydraulic exercises were performed, which were validated by comparing the application results against results obtained from three different methodologies (Goal Seek, Newton-Rapson, Hcanales®).
Finally, the development of algorithms for operating systems compatible with iOS and Windows is recommended, which expands the coverage of the application to a greater number of users. This application has been downloaded in Colombia, Bolivia, Peru, Costa Rica and Algeria.
