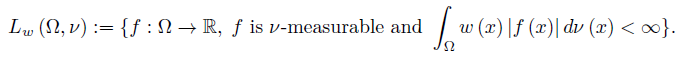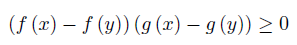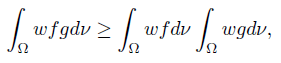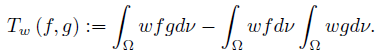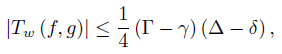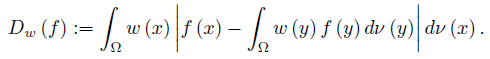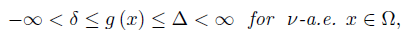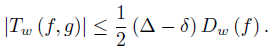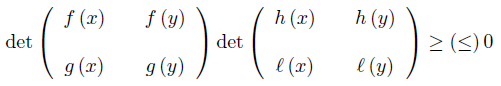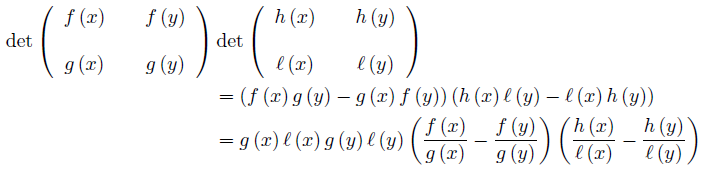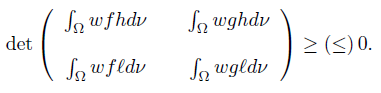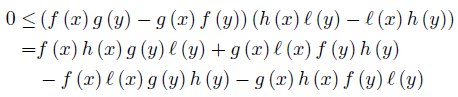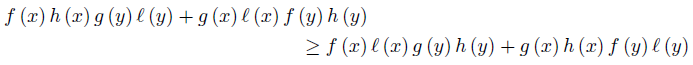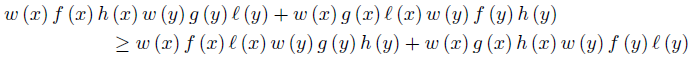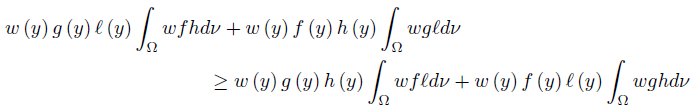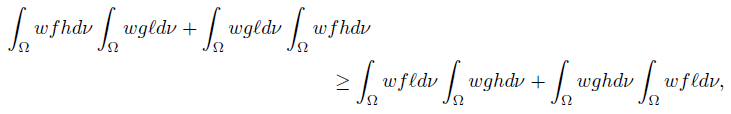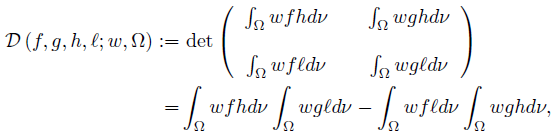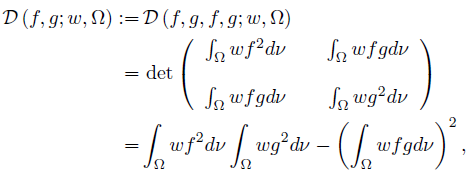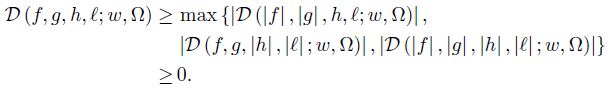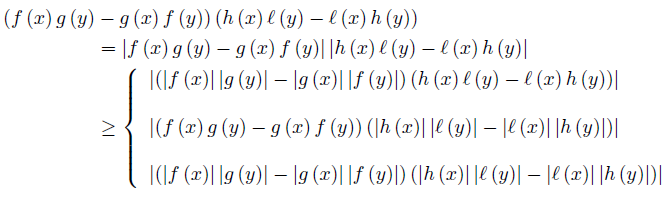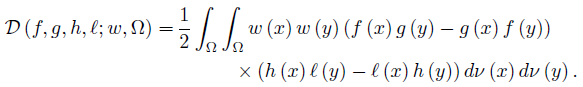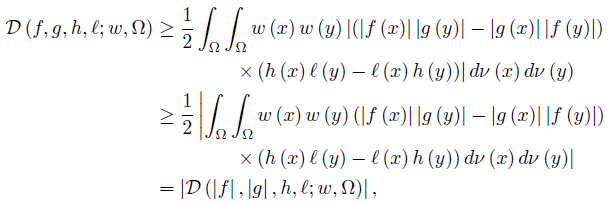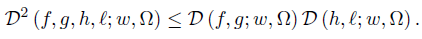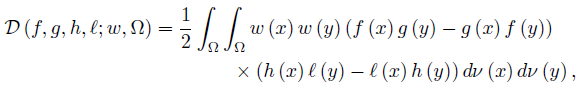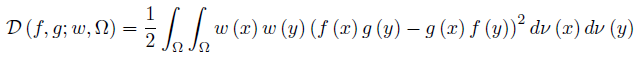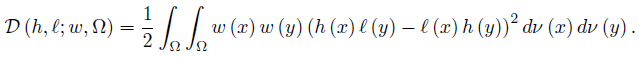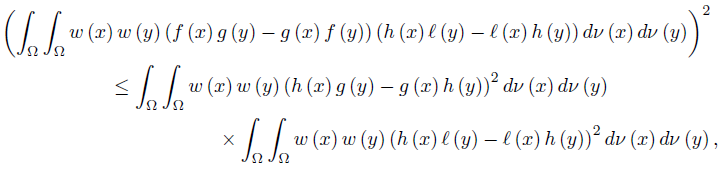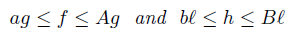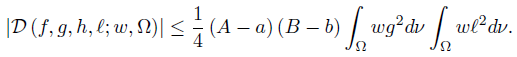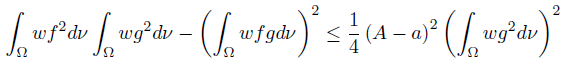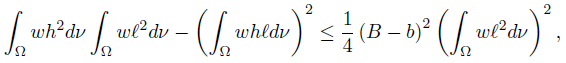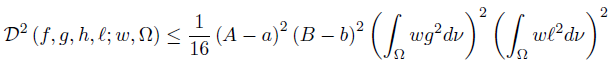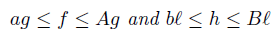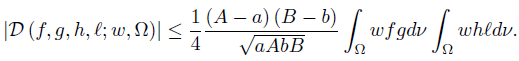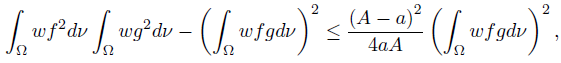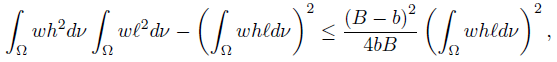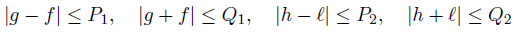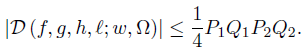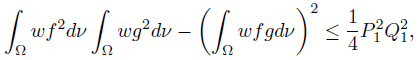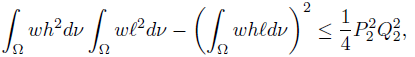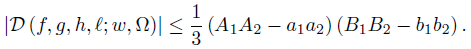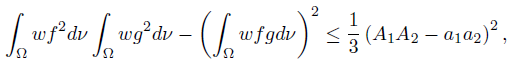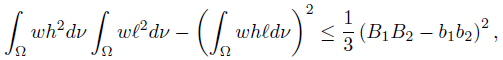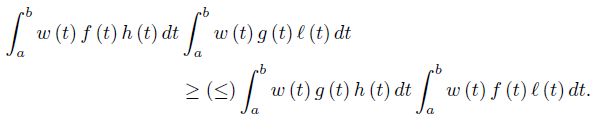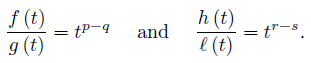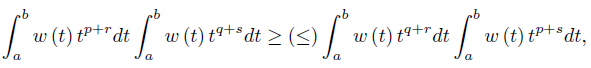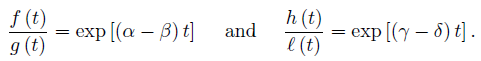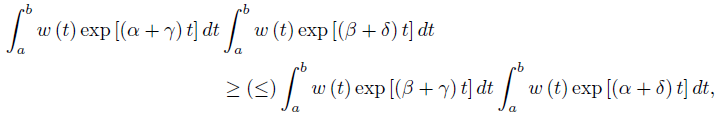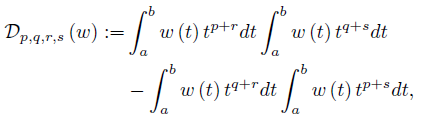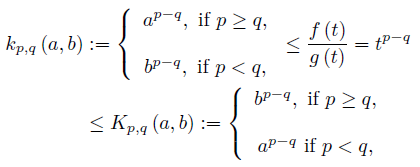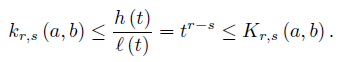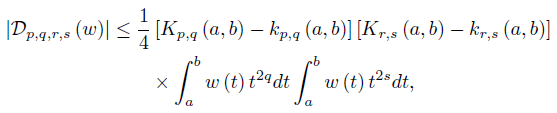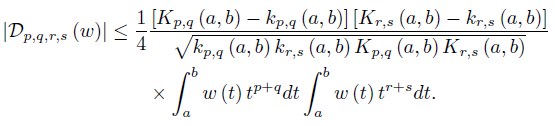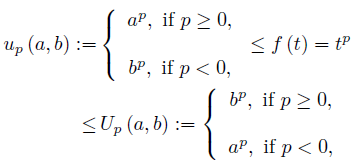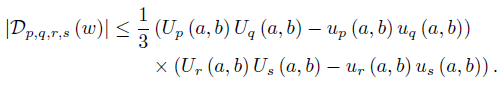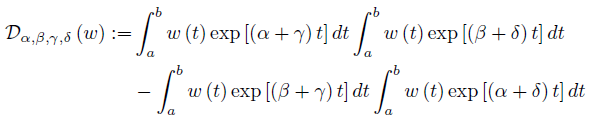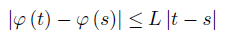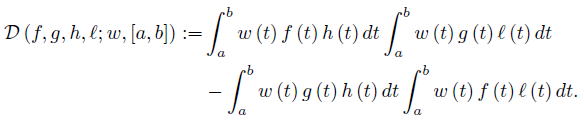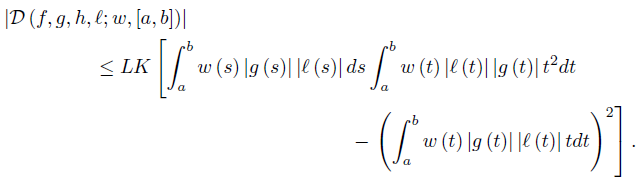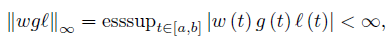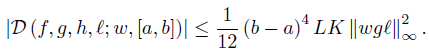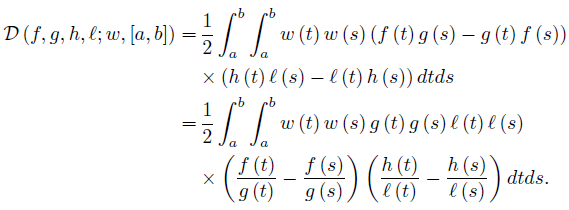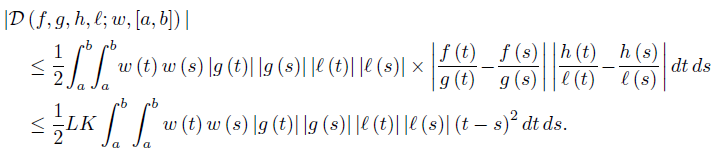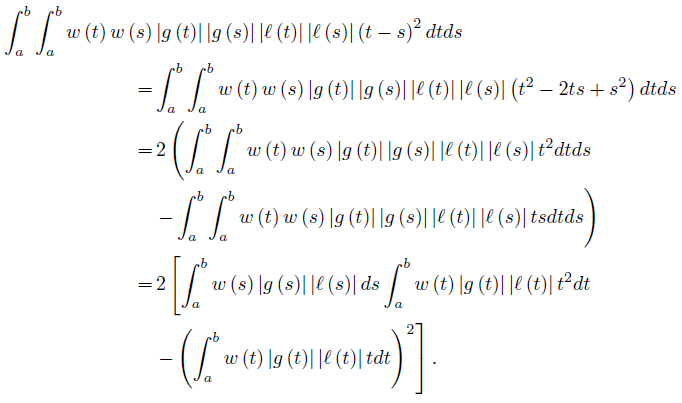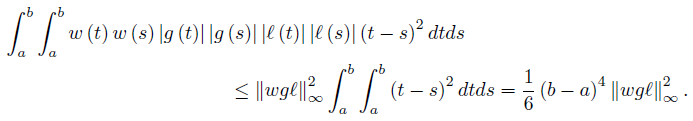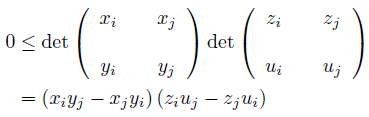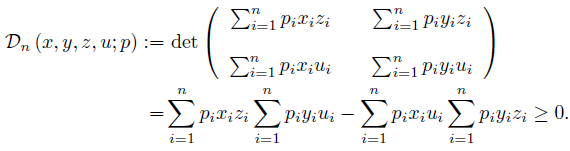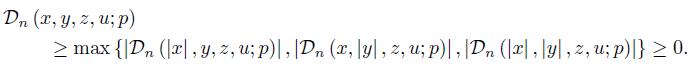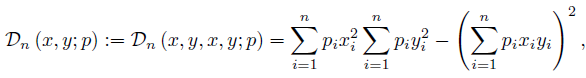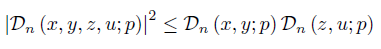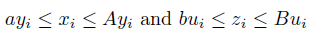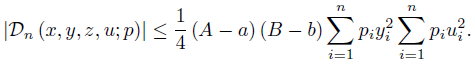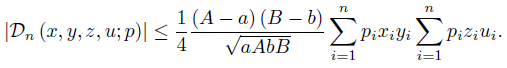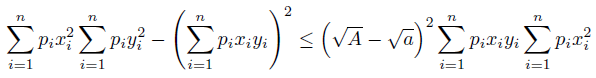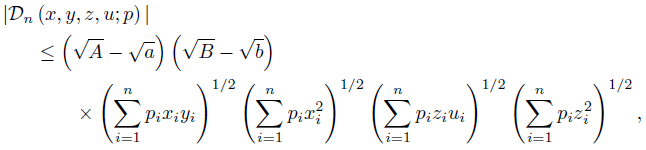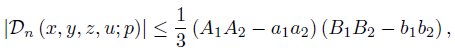1. Introduction

Let (Ω, A, ν) be a measurable space consisting of a set Ω, a σ-algebra A of subsets of Ω and a countably additive and positive measure ν on A with values in [0, +∞] . For a ν-measurable function w : Ω → , with w (x) ≥ 0 for ν-a.e. (almost every) x ∈ Ω, consider the Lebesgue space

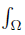For simplicity of notation we write everywhere in the sequel wdν instead of w (x) dν (x). Assume also that 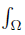wdν = 1.

We say that the pair of measurable functions (f, g) are synchronous on Ω if

for ν-a.e. x, y ∈ Ω. If the inequality reverses in (1), the functions are called asynchronous on Ω.

If (f, g) are synchronous on Ω and f, g, fg ∈ L_w (Ω, ν), then the following inequality, that is known in the literature as Chebyshev’s Inequality, holds:

where w (x) ≥ 0 for ν-a.e. (almost every) x ∈ Ω and 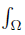wdν = 1.

If f, g : Ω → 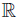are ν-measurable functions and f, g, fg ∈ L_w(Ω, ν), then we may consider the Chebyshev functional

The following result is known in the literature as the Grüss inequality:

provided

for ν-a.e. x ∈ Ω.

The constant 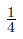is sharp in the sense that it cannot be replaced by a smaller quantity.

If f ∈ L_w (Ω, ν), then we may define

The following refinement of Grüss inequality in the general setting of measure spaces is due to Cerone & Dragomir [¹]:

Theorem 1.1. Let w, f, g: Ω → 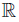be ν-measurable functions with w ≥ 0 ν-a.e. on Ω and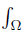wdν = 1. If f, g, fg ∈ L_w (Ω, ν) and there exist constants δ, ∆ such that

then we have the inequality

The constant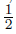is sharp in the sense that it cannot be replaced by a smaller quantity.

Motivated by the above results, we introduce in this paper the concept of quadruple D−synchronous functions that generalizes the concept of a pair of synchronous functions, we establish an inequality similar to Chebyshev inequality and also provide some CauchyBunyakovsky-Schwarz type inequalities for a functional associated with this quadruple. Some applications for univariate functions of real variable are given. Discrete inequalities are also stated.

2. D−Synchronous functions

Let (Ω, A, ν) be a measurable space and f, g, h, ℓ : Ω → 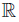be four ν-measurable functions on Ω.

Definition 2.1. The quadruple (f, g, h, ℓ) is called D−Synchronous (D−Asynchronous) on Ω if

for ν-a.e. (almost every) x, y ∈ Ω.

This concept is a generalization of synchronous functions, since for g = 1, ℓ = 1 the quadruple (f, g, h, ℓ) is D−Synchronous if, and only if, (f, h) is synchronous on Ω.

If g, ℓ 0 ν-a.e on Ω, then

for ν-a.e. x, y ∈ Ω. So, if gℓ > 0 ν-a.e on Ω the quadruple (f, g, h, ℓ) is D−Synchronous if, and only if, 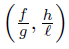is synchronous on Ω.

Theorem 2.2. Let f, g, h, ℓ: Ω → 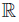be ν-measurable functions on Ω and such that the quadruple (f, g, h, ℓ) is D-Synchronous (D−Asynchronous), w ≥ 0 a.e. on Ω with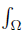wdν = 1 and fh, gℓ, gh, f ℓ ∈ L_w (Ω, ν). Then,

Proof. Since the quadruple (f, g, h, ℓ) is D−Synchronous, then

for ν-a.e. x, y ∈ Ω.

This is equivalent to

for ν-a.e. x, y ∈ Ω.

Multiply (12) by w (x) w (y) ≥ 0 to get

for ν-a.e. x, y ∈ Ω.

If we integrate the inequality (13) over x ∈ Ω, then we get

for ν-a.e. y ∈ Ω.

Finally, if we integrate the inequality (14) over y ∈ Ω, then we get

which is equivalent to the desired result (10).

Corollary 2.3. Let f, g, h, ℓ: Ω → 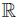be ν-measurable functions on Ω and such that gℓ > 0 ν-a.e on Ω, 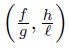is synchronous (asynchronous) on Ω, w ≥ 0 a.e. on Ω with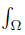wdν = 1 and fh, gℓ, gh, fℓ ∈ L_w (Ω, ν) ; then the inequality (10) is valid.

Let f, g, h, ℓ : Ω → 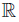be ν-measurable functions on Ω , w ≥ 0 a.e. on Ω with 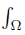wdν = 1 and fh, gℓ, gh, fℓ ∈ L_w (Ω, ν) ; then we can consider the functionals

and, for (f, g) = (h, ℓ),

provided f ², g² ∈ L_w (Ω, ν).

We can improve the inequality (10) as follows:

Theorem 2.4. Let f, g, h, ℓ: Ω → 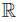be ν-measurable functions on Ω and such that the quadruple (f, g, h, ℓ) is D−Synchronous, w ≥ 0 a.e. on Ω with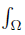wdν = 1 and fh, gℓ, gh, fℓ ∈ L_w (Ω, ν) ; then,

Proof. We use the continuity property of the modulus, namely

Since (f, g, h, ℓ) is D−Synchronous, then

for ν-a.e. x, y ∈ Ω.

As in the proof of Theorem 2.2, we have the identity

By using the identity (19) and the first branch in (18) we have

which proves the first part of (17).

The second and third part of (17) can be proved in a similar way and details are omitted.

3. Further results for the functional D

We have the following Schwarz’s type inequality for the functional D:

Theorem 3.1. Let f, g, h, ℓ: Ω → 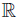be ν-measurable functions on Ω , w ≥ 0 a.e. on Ω with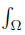wdν = 1 and f², g², h², ℓ² ∈ L_w (Ω, ν). Then,

Proof. As in the proof of Theorem 2.4, we have the identities

and

By the Cauchy-Bunyakovsky-Schwarz double integral inequality we have

which produces the desired result (20).

Corollary 3.2. Let f, g, h, ℓ: Ω → 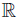be ν-measurable functions on Ω with g², ℓ² ∈ L_w (Ω, ν), w ≥ 0 a.e. on Ω with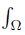wdν = 1, and a, A, b, B ∈ 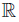such that A > a, B > b,

ν-a.e. on Ω. Then,

Proof. In [²] (see also [⁴, p. 8]) we proved the following reverse of Cauchy-BunyakovskySchwarz integral inequality

provided that ag ≤ f ≤ Ag ν-a.e. on Ω and g² ∈ L_w (Ω, ν).

Since, we also have

provided that bℓ ≤ h ≤ Bℓ ν-a.e. on Ω and ℓ² ∈ L_w (Ω, ν). Then, by (20) we have

that is equivalent to the desired result (22).

For positive margins we also have:

Corollary 3.3. Let f, g, h, ℓ: Ω → be four ν-measurable functions on Ω with g², ℓ² ∈ L_w (Ω, ν), w ≥ 0 a.e. on Ω withwdν = 1, and a, A, b, B > 0 such that A > a, B > b,

ν-a.e. on Ω. Then we have

Proof. In [³] (see also [⁴, p. 16]) we proved the following reverse of Cauchy-BunyakovskySchwarz integral inequality:

whenever ag ≤ f ≤ Ag ν-a.e. on Ω.

Since

provided bℓ ≤ h ≤ Bℓ ν-a.e. on Ω, then by (20) we get the desired result (24).

If bounds for the sum and difference are available, then we have:

Corollary 3.4. Let f, g, h, ℓ : Ω → be ν-measurable functions on Ω with g² , ℓ² ∈ L_w (Ω, ν), w ≥ 0 a.e. on Ω withwdν = 1. Assume that there exists the constants P₁, Q₁, P₂, Q₂such that

a.e. on Ω; then,

Proof. In the recent paper [⁵] we obtained amongst other the following reverse of CauchyBunyakovsky-Schwarz integral inequality:

provided |g − f| ≤ P₁, |g + f| ≤ Q₁ a.e. on Ω.

Since

if |h − ℓ| ≤ P₂, |h + ℓ| ≤ Q₂ a.e. on Ω, then by (20) we get the desired result (26).

If bounds for each function are available, then we have:

Corollary 3.5. Let f, g, h, ℓ: Ω → 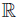be ν-measurable functions on Ω and w ≥ 0 a.e. on Ω with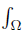wdν = 1. Assume that there exists the constants ai, A_i , b_i and B_i with i ∈ {1, 2} such that

and

a.e. on Ω; then,

Proof. We use the following Ozeki’s type inequality obtained in [⁶]:

provided 0 < a₁ ≤ f ≤ A₁ < ∞, 0 < a₂ ≤ g ≤ A₂ < ∞ a.e. on Ω.

Since

when 0 < b₁ ≤ h ≤ B₁ < ∞, 0 < b₂ ≤ ℓ ≤ B₂ < ∞ a.e. on Ω, then by (20) we get the desired result (29).

4. Results for univariate functions

Let Ω = [a, b] be an interval of real numbers, and assume that f, g, h, ℓ : [a, b] → 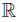are measurable D−Synchronous (D−Aynchronous), w ≥ 0 a.e. on [a, b] with 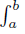w (t) dt = 1 and fh, gℓ, gh, fℓ ∈ L_w ([a, b]) ; then,

Now, assume that [a, b] ⊂ (0, ∞) and take f (t) = t^p, g (t) = t^q, h (t) = t^r and ℓ (t) = t^s with p, q, r, s ∈ . Then,

If (p − q) (r − s) > 0, then the functions 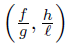have the same monotonicity on [a, b] while if (p − q) (r − s) < 0 then 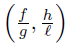have opposite monotonicity on [a, b] . Therefore, by (30) we have for any nonnegative integrable function w with w (t) dt = 1 that

provided (p − q) (r − s) > (<) 0.

Assume that [a, b] ⊂ (0, ∞) and take f (t) = exp (αt), g (t) = exp (βt), h (t) = exp (γt) and ℓ (t) = exp (δt), with α, β, γ, δ ∈ 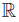. Then,

If (α − β) (γ − δ) > 0, then the functions 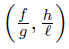have the same monotonicity on [a, b] , while if (α − β) (γ − δ) < 0 then 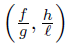have opposite monotonicity on [a, b] . Therefore, by (30) we have for any nonnegative integrable function w with 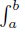w (t) dt = 1 that

provided (α − β) (γ − δ) > (<) 0.

Consider the functional

for any nonnegative integrable function w with 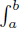w (t) dt = 1, and p, q, r, s ∈ .

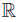We observe that for t ∈ [a, b] ⊂ (0, ∞) we have

and, similarly,

Using the inequality (22) we have

while from (24) we have

We also have for t ∈ [a, b] ⊂ (0, ∞) that

and the corresponding bounds for g (t) = t^q, h (t) = t^r and ℓ (t) = t^s, with p, q, r, s ∈ 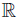. Making use of the inequality (29) we get

Similar results may be stated for the functional

for any nonnegative integrable function w with 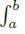w (t) dt = 1, for α, β, γ, δ ∈ 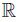and [a, b] ⊂ (0, ∞). Details are omitted.

We say that the function φ : [a, b] → 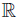is Lipschitzian with the constant L > 0 if

for any t, s ∈ [a, b] .

Define the functional

In the next result we provided two upper bounds in terms of Lipschitzian constants:

Theorem 4.1. Let f, g, h, ℓ: [a, b] → 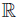be measurable functions and w ≥ 0 a.e. on [a, b] with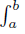w (t) dt = 1.

(i) If g (t), ℓ (t) 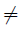0 for any t ∈ [a, b] , and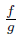is Lipschitzian with the constant L > 0, and is Lipschitzian with the constant K 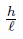> 0, and gℓ, gℓe² ∈ L_w ([a, b]) with e (t) = t, t ∈ [a, b], then

(ii) If, in addition, we have wgℓ ∈ L_∞ [a, b] and

then

Proof. We have

By taking modulus in this equality, we get

Now, observe that

On making use of (40) and (41) we get the desired result (38).

If wgℓ ∈ L_∞ [a, b] , then

Therefore, by inequalities (40) and (42) we obtain the desired result (39).

5. Discrete inequalities

Consider the n-tuples of real numbers x = (x₁, ..., x_n), y = (y₁, ..., y_n), z = (z₁, ..., z_n) and u = (u₁, ..., u_n). We say that the quadruple (x, y, z, u) is D−Synchronous if

for any i, j ∈ {1, ..., n} .

If p = (p₁, ..., p_n) is a probability distribution, namely, p_i ≥ 0 for any i ∈ {1, ..., n} and 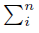=1 p_i = 1, and the quadruple (x, y, z, u) is D−Synchronous, then by (10) we have:

For an n-tuples of real numbers x = (x₁, ..., x_n), we denote by |x| := (|x₁| , ..., |x_n|). On making use of the inequality (17), then for any D−Synchronous quadruple (x, y, z, u) and for any probability distribution p = (p₁, ..., p_n) we have

Observe that if we consider

then by (20) we have

for any quadruple (x, y, z, u) and any probability distribution p = (p₁, ..., p_n).

If a, A, b, B ∈ and (x, y, z, u) are such that A > a, B > b,

for any i ∈ {1, ..., n} , then by (22) we have

If a, A, b, B > 0 and condition (47) is valid, then by (24) we have

Now, if we use the Klamkin-McLenaghan’s inequality

that holds for x, y satisfying the condition (47) with A, a > 0, then by (46) we get

provided (x, y, z, u) satisfy (47) with a, A, b, B > 0.

Now, assume that

and

for any i ∈ {1, ..., n} ; then by (29) we get

for any probability distribution p = (p₁, ..., p_n ).