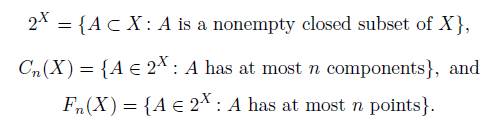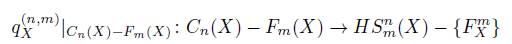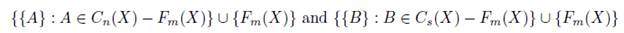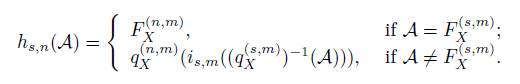1. Introduction

Recently, the study of the (n, m)−fold hyperspace suspension of continua has been ad-dressed in [¹], [⁵], [⁶], [⁸]-[¹⁰], [¹⁴], [¹⁵], [¹⁷]-[¹⁹], [²¹], [²²], [²⁴].

A continuum is a nondegenerate compact connected metric space. A subcontinuum is a continuum contained in a continuum X. The set of positive integers is denoted by N.

Given a continuum X and n ∈ N, we consider the following hyperspaces of X:

All these hyperspaces are metrized by the Hausdorff metric H [¹¹, Theorem 2.2]. The hyperspaces F _n (X) and C _n (X) are called the n−fold symmetric product of X and the n−fold hyperspace of X, respectively, we will write C(X) instead of C ₁(X). It is impor-tant to note that whenever X is a continuum, all these hyperspaces are continua (see [¹⁹, 1.8.8, 1.8.9, 1.8.12]).

Let X be a continuum and let n, m ∈ N be such that m ≤ n. In 1979 Sam B. Nadler, Jr. introduced the hyperspace suspension of a continuum X as the quotient space C(X)/F ₁(X) obtained from C(X) by shrinking F ₁(X) to a one-point set with the quotient topology, denoted by HS(X), see [²⁴]. Later, in 2004 Sergio Macías in-troduced the n−fold hyperspace suspension of a continuum X as the quotient space C _n (X)/F _n (X), denoted by HS _n (X), see [¹⁷]. Afterward in 2008, Juan Carlos Macías introduced the n−fold pseudo-hyperspace suspension of a continuum X as the quotient space C _n (X)/F ₁(X), denoted by P HS _n (X), see [¹⁵]. Recently, in 2018 José G. Anaya, David Maya, and Francisco Vázquez-Juárez introduced the (n, m)−fold hyperspace sus-pension of X as the quotient space C _n (X)/F _m (X) obtained from C _n (X) by shrinking F _m (X) to a one-point set with the quotient topology, denoted by HS _m ⁿ (X), see [¹]. The fact that HS _m ⁿ (X) is a continuum follows from [²⁵, Theorem 3.10]. The study of (n, m)−fold hyperspace suspension is, therefore, a generalization of the latter research.

The main topics of this paper are summed up in the following general problem.

Problem 1. Given a continuum X and n, m ∈ N satisfying that m ≤ n, is there a topological property P that holds on HS _m ⁿ (X)?

Related to Problem 1, the aim of this paper is to prove that:

(a) If X is a continuum and n, m ∈ ℕ with m ≤ n, then HS _m ⁿ (X) contains an n−cell (see Theorem 3.1).

(b)If X is a continuum and n, m ∈ ℕ with m ≤ n, then HS _m ⁿ (X) has property (b) (see Theorem 3.4).

(c)If X is a continuum and n, m ∈ ℕ with m ≤ n, then HS _m ⁿ (X) is unicoherent (see Theorem 3.5).

(d)If X is a continuum and n, m ∈ ℕ with m ≤ n, then HS _m ⁿ (X) is colocally connected (see Theorem 3.6).

(e)If X is a continuum and n, m ∈ ℕ with m ≤ n, then HS _m ⁿ (X) is aposyndetic (see Corollary 3.7).

(f)If X is a continuum and n, m ∈ ℕ with m ≤ n, then HS _m ⁿ (X) is finitely aposyndetic (see Theorem 3.8).

It is important to notice that those results that give a solution to Problem 1 are indeed generalizing Theorems 3.7, 4.1, and 4.2 as well as Corollary 4.3 and 4.4 proved by S. Macías in [¹⁷], respectively.

On the other hand, we present two results related to finite-dimensional Cantor manifolds, see Theorem 3.9 and Theorem 3.10.

2. Definitions and preliminary results

In this section, we present several results (with their references) that will be useful through this paper.

Given a subset A in a metric space X, int _X (A) denotes the interior of A in X. If d is the metric of a continuum X, ε > 0, A ⊂ X, and a ∈ X, then the set {x ∈ X: d(a, x) < ε} is denoted by Bd(a, ε), or B(a, ε) when there is no possibility of confusion. Let N(ε, A) =∪ {B(a, ε) : a ∈ A}. Given subsets U ₁ , . . . , U _r of X, with r, n ∈ ℕ, let

U ₁ , . . . , U _{r n} = {A ∈ C _n (X) : A ⊂ U ₁ ∪ · · · ∪ U _r and A ∩ U _i # ∅, for each i ∈ {1, . . . , r}}.

It is known by [¹¹, Theorem 1.2] that the family of all sets of the form U ₁ , . . . , U _{r n} , where r ∈ ℕ and each U _i is an open subset of X, is a basis for the topology in C _n (X), known as Vietoris topology.

Recall that a useful tool in the theory of hyperspaces is the existence of order arcs. Given a continuum X, an order arc in 2 ^X is a continuous function α: [0, 1] → 2 ^X such that α(s) ⊊ α(t), for each s, t ∈ [0, 1] with s < t. If A, B ∈ 2 ^X satisfy that α(0) = A and α(1) = B, then we say that α is an order arc from A to B.

Lemma 2.1. [²³, (1.8)] Let A, B ∈ 2 ^X be such that A ≠ B. Then, the following two statements are equivalent:

(a)there exists an order arc in 2 ^X from A to B,

(b)A ⊂ B and each component of B intersects A.

An arc is any space homeomorphic to [0, 1]. Given n ∈ ℕ, an n−cell is a space which is homeomorphic to [0, 1] ⁿ . A continuum is said to be decomposable provided it can be written as the union of two of its proper subcontinua.

Lemma 2.2. [¹⁶, Theorem 3.4] Let X be a continuum and n ∈ ℕ. Then, C _n (X) contains an n−cell.

Lemma 2.3. [¹⁶, Theorem 3.5] Let X be a continuum and n ∈ N. If X contains n pairwise disjoint decomposable subcontinua, then C _n (X) contains a 2n−cell.

Lemma 2.4. [⁷, Proposition 1(a), p. 798] Let X be a continuum and n ∈ ℕ. If V ⊂ X is an n−cell and U is an open set in X such that U ∩ V # ∅, then there is an n−cell T ⊂U∩V.

Recall that, as in [⁴, p. 16], let A, B be two sets with equivalence relations R and S, respectively. A function f: A → B is said to be relation-preserving provided that aRa ^′ implies f(a)Sf(a ^′ ).

Lemma 2.5. [⁴, Theorem 4.3, p. 126] Let X, Y be spaces with equivalence relations R and S, respectively, and let f: X → Y be a relation-preserving, continuous function. Then, passing to the quotient, the function f _∗ : X/R → Y /S is also continuous.

A continuum X has the property (b) provided that each continuous function from X into the unit circle S ¹ is homotopic to a constant function.

We say that a continuum X is unicoherent provided that for each pair A and B of subcontinua of X such that X = A ∪ B, A ∩ B is connected.

Lemma 2.6. [¹⁶, Theorem 4.7] Let X be a connected metric space. If X has the property (b), then X is unicoherent.

Lemma 2.7. [¹⁶, Theorem 4.8] Let X be a continuum and n ∈ ℕ. Then, C _n (X) has the property (b). In particular, we have that C _n (X) is unicoherent.

Lemma 2.8. [¹¹, Theorem 19.7] If a continuum is contractible with respect to S ¹ , then the continuum is unicoherent.

A continuum is said to be colocally connected when each one of its points has a local base of open sets whose complement is connected.

The continuum X is aposyndetic if for each pair of points x and y of X, there exists a subcontinuum W of X such that x ∈ int _X (W ) ⊂ W ⊂ X − {y }. A continuum X is finitely aposyndetic provided that for each finite subset F of X and each point x ∈ X −F , there exists a subcontinuum W of X such that x ∈ int _X (W ) ⊂ W ⊂ X − F .

Lemma 2.9. [², Corollary 1] If X is an unicoherent and aposyndetic continuum, then X is finitely aposyndetic.

We use the following notations: dim[X] stands for the dimension of X, dim _p [X] stands for the dimension of X at the point p ∈ X, as in [²⁶, p. 5].

Lemma 2.10. [⁶, Theorem 3.1] If X is a finite-dimensional continuum and n, m ∈ N with m ≤ n, then dim[C _n (X)] is finite if and only if dim[HS _m ⁿ (X)] is finite. Moreover, if either dim[C _n (X)] is finite or dim[HS _m ⁿ (X)] is finite, then dim[C _n (X)] = dim[HS _m ⁿ (X)].

Lemma 2.11. [¹³, Theorem 2.1] If X is a continuum such that dim[X] = 2, then dim[C(X)] is infinite.

Lemma 2.12. [¹¹, Theorem 72.5] If X is a continuum such that dim[X] ≥ 3, then dim[C(X)] is infinite.

Lemma 2.13. [³, Lemma 3.1] If X is a finite-dimensional continuum and n ∈ N, then dim[F _n (X)] ≤ n · dim[X].

Lemma 2.14. [²⁶, 7.3] Let X, Y, Z be separable metric spaces such that X = Y ∪ Z, where dim[Y ] ≤ n and dim[Z] ≤ n. If at least one of Y and Z is closed in X, then dim[X] ≤ n.

A finite-dimensional continuum X is a Cantor manifold if for any subset A of X such that dim[A] ≤ dim[X] − 2, then X − A is connected.

Lemma 2.15. [²⁰, Theorem 4.6] The hyperspaces C _n ([0, 1]) and C _n (S ¹) are 2n−dimensional Cantor manifolds, for each n ∈ ℕ.

A continuous function between continua X and Y is said to be monotone provided that point inverses are connected (equivalently if the inverse image of each subcontinuum of y is connected).

For a continuum X and n, m ∈ ℕ satisfying that m ≤ n, the symbol q _X ^(n,m) denotes the natural projection q _X ^(n,m) : C _n (X) → HS _m ⁿ (X), and F _X ^m denotes the element of q _X ^(n,m) (F _m (X)). Notice that

is a homeomorphism.

We shall make use of other concepts not defined here, which will be taken as in [¹⁹].

3. Main Results

The following result extends [¹⁷, Theorem 3.7].

Theorem 3.1. Let X be a continuum and n, m ∈ ℕ with m ≤ n. Then, HS _m ⁿ (X) contains an n−cell.

Proof. By Lemma 2.2, C _n (X) contains an n−cell M. Moreover, since C _n (X) −F _m (X) isa dense open subset of C _n (X), we have that ((C _n (X)−Fm(X))∩M̸= ∅. By Lemma 2.4, there exists an n−cell N such that N ⊂ Cn(X)−Fm(X). Thus, by (1), HS ⁿ _m (X) contains an n−cell.

The next result extends [¹⁷, Theorem 3.8].

Theorem 3.2. If n, m ∈ N with m ≤ n and X is a continuum that contains n pairwise disjoint decomposable subcontinua, then HS _m ⁿ (X) contains a 2n−cell.

Proof. By Lemma 2.3, C _n (X) contains a 2n−cellM. Moreover, since C _n (X)−F _m (X) is a dense open subset of C _n (X), we have that ((C _n (X)−F _m (X))∩M̸= ∅. By Lemma 2.4, there exists a 2n−cell N such that N ⊂ C _n (X)−F _m (X). Thus, by (1), HS ⁿ _m (X) contains a 2n−cell.

The following result extends [¹⁸, Theorem 4.1].

Theorem 3.3. Let X be a continuum and n, m, s ∈ ℕ with m ≤ s < n. Then, HS _m ^s (X) can be embedded in HS _m ⁿ (X).

Proof. Let i _s,n : C _s (X) → C _n (X) be the inclusion function, q _X ^(s,m) : C _s (X) → HS _m ^s (X) and q _X ^(n,m) : C _n (X) → HS _m ⁿ (X) be quotient functions. We denote q _X ^(s,m) (F _m (X)) = F _X ^(s,m) and q _X ^(n,m) (F _m (X)) = F _X ^(n,m) . Since

are partitions of C _n (X) and C _s (X), respectively; then i _s,n is a relation-preserving and continuous. Now, let h _s,n : HS _m ^s (X) → HS _m ⁿ (X) be given by

Notice that h _s,n is a continuous function by Lemma 2.5. Moreover, as h _s,n is defined, it is clear that h _s,n is a one-to-one function. Since the spaces are compact, h _s,n is an embedding.

The next result extends [¹⁷, Theorem 4.1].

Theorem 3.4. Let X be a continuum and n, m ∈ ℕ with m ≤ n. Then, HS _m ⁿ (X) has property (b).

Proof. Let A ∈ HS _m ⁿ (X). If A = F _X ^m , then (q _X ^(n,m) ) ⁻¹ ( A) = F _m (X) which is a connected subset of C _n (X). On the other hand, if A # F _X ^m , using relation (1), then (q _X ^(n,m) ) ⁻¹ (A) is a one-point set. Hence, (q _X ^(n,m) ) ⁻¹ (A) is a connected subset of C _n (X). Therefore, q _X ^(n,m) is a monotone function. By Lemma 2.7, C _n (X) has property (b). Since q _X ^(n,m) (C _n (X)) = HS _m ⁿ (X) and [¹², Theorem 2, p.434], we conclude that HS _m ⁿ (X) has the property (b).

Theorem 3.5. Let X be a continuum and n, m ∈ ℕ with m ≤ n. Then, HS _m ⁿ (X) is unicoherent.

Proof. Applying Theorem 3.4 and Lemma 2.6, the result follows.

The following result extends [¹⁷, Theorem 4.2].

Theorem 3.6. Let X be a continuum and n, m ∈ ℕ with m ≤ n. Then, HS _m ⁿ (X) is colocally connected.

Proof. Case n = m = 1 is already proved in [⁵, Theorem 4.1].

Suppose n ≥ 2 and let A ∈ HS _m ⁿ (X). We are going to consider three cases:

Case 1. A = F _X ^m .

For any ε > 0, let U _ε = B _H (F _m (X), ε). Notice that {q _X ^(n,m) (U _ε ) : ε > 0} forms a base of open sets about F _X ^m . Fix ε > 0. Let B ∈ HS _m ⁿ (X) − q _X ^(n,m) (U _ε ). Thus, (q _X ^(n,m) ) ⁻¹ ( B) ∈ C _n (X) − U _ε . By Lemma 2.1, there exists an order arc α: [0, 1] → C _n (X) such that α(0) = (q _X ^(n,m) ) ⁻¹ (B) and α(1) = X and α([0, 1]) ⊂ C _n (X) − U _ε . Notice that q _X ^(n,m) ◦ α: [0, 1] → HS _m ⁿ (X) is an arc from B to q _X ^(n,m) (X) satisfying (q _X ^(n,m) ◦α)([0, 1]) ⊂ HS _m ⁿ (X)− (U _ε ), which implies that this space is arcwise connected.

Case 2. A = q _X ^(n,m) (X).

For any ε > 0, let U _ε = B _H (X, ε). Observe that {q _X ^(n,m) (U _ε ) : ε > 0} forms a base of open sets about q _X ^(n,m) (X). Fix ε > 0. Let B ∈ HS _m ⁿ (X) − q _X ^(n,m) (U _ε ). Thus, (q _X ^(n,m) ) ⁻¹ (B) ∈ C _n (X) − U _ε . Let D ∈ F _m ((q _X ^(n,m) ) ⁻¹ (B)). By Lemma 2.1, there exists an order arc a : [0, 1] → C _n (X) such that α(0) = D and α(1) = (q _X ^(n,m) ) ⁻¹ (B). Moreover, α([0, 1]) ⊂ C _n (X) − U _ε . Hence, q _X ^(n,m) ◦ α: [0, 1] → C _n (X) is an arc such that (q _X ^(n,m) ◦ α)(0) = F _X ^m , (q _X ^(n,m) ◦ α)(1) = D and (q _X ^(n,m) ◦ α)([0, 1]) ⊂ HS _m ⁿ (X) − q _X ^(n,m) (U _ε ). Therefore, HS _m ⁿ (X) − q _X ^(n,m) (U _ε ) is an arcwise connected space.

Case 3. A ∈ HS _m ⁿ (X) − {F _X ^m , q _X ^(n,m) (X)}.

For any ε > 0, let U _ε = B _H ((q _X ^(n,m) ) ⁻¹ (A), ε). Thus, {q _X ^(n,m) (U _ε ) : ε > 0} forms a base of open sets about A. Fix ε > 0 such that q _X (U _ε ) ∩ {F _X ^m , q _X ^(n,m) (X)} = ∅. Let B ∈ HS _m ⁿ (X) − q _X ^(n,m) (U _ε ). If (q _X ^(n,m) ) ⁻¹ (B) ⊈ (q _X ^(n,m) ) ⁻¹ (A), by Lemma 2.1 there exists an order arc α: [0, 1] → C _n (X) such that α(0) = (q _X ^(n,m) ) ⁻¹ (B) and α(1) = X. Thus, α([0, 1]) ⊂ C _n (X)−B _H ((q _X ^(n,m) ) ⁻¹ (A), ε). Hence, q _X ^(n,m) ◦α is an arc from B to q _X ^(n,m) (X) such that q _X ^(n,m) ◦ α ⊂ HS _m ⁿ (X) − U _ε , as desired.

On the other hand, suppose that (q ^(n,m) _X ) ⁻¹ (B) ⊂ (q ^(n,m) _X ) ⁻¹ (A). Let D ∈ F _m ((q ^(n,m) _X ) ⁻¹ (B)). By Lemma 2.1, there exists an order arc β: [0, 1] → C _n (X) such that β(0) = D and β(1) = (q ^(n,m) _X ) ⁻¹ (B). Thus, β([0, 1]) is contained in C _n (X) − BH((q ^(n,m) _X ) ⁻¹ (A), ε). Hence, q(n,m) X ◦ β: [0, 1] → HSnm (X) is an arc from F ^m _X to B and (q ^(n,m) _X ◦ β)([0, 1]) ⊂ HS ⁿ _m (X) − q ^(n,m) _X (U _ε ). Therefore, the last space is arcwise connected.

Since colocal connectedness implies aposyndesis, we have the next result which extends [¹⁷, Corollary 4.3].

Corollary 3.7. Let X be a continuum and n, m ∈ ℕ with m ≤ n. Then, HS _m ⁿ (X) is aposyndetic.

From this, we can prove the following result which extends [¹⁷, Corollary 4.4].

Theorem 3.8. Let X be a continuum and n, m ∈ ℕ with m ≤ n. Then, HS _m ⁿ (X) is finitely aposyndetic.

Proof. By Theorem 3.5, HS _m ⁿ (X) is unicoherent. By Corollary 3.7, HS _m ⁿ (X) is aposyn-detic. Finally, by Lemma 2.9, any aposyndetic unicoherent continuum is finitely aposyndetic.

The following result extends [¹⁷, Theorem 3.9].

Theorem 3.9. Let X be a continuum and n, m ∈ ℕ with m ≤ n. If C _n (X) is a finite- dimensional Cantor manifold such that dim[C _n (X)] ≥ n + 2, then HS _m ⁿ (X) is a finite- dimensional Cantor manifold.

Proof. Let k = dim[C _n (X)]. According to Lemma 2.10, dim[HS _m ⁿ (X)] = k. Suppose HS _m ⁿ (X) is not a Cantor manifold. Hence, there exists a subset A of HS _m ⁿ (X) such that dim[A] ≤ k−2 and HS _m ⁿ (X)−A is not connected. Hence, there exist a separation A ₁ , A ₂ of HS _m ⁿ (X) − A. Furthermore, by [27, (1.4), p. 43], there exist a closed subset A ^′ of A and nonempty open subsets D, E of HS _m ⁿ (X) such that HS _m ⁿ (X) − A ^′ = D ∪ E where D ⊂ A ₁ and E ⊂ A ₂. Hence, C _n (X) − (q _X ^(n,m) ) ⁻¹ (A ^′ ) = (q _X ^(n,m) ) ⁻¹ (D) ∪ (q _X ^(n,m) ) ⁻¹ (E), where (q _X ^(n,m) ) ⁻¹ (D) and (q _X ^(n,m) ) ⁻¹ (E) are disjoint open subsets of C _n (X). In order to reach a contradiction, we will see that dim[(q _X ^(n,m) ) ⁻¹ (A ^′ )] ≤ k − 2 so that, C _n (X) is not a Cantor manifold. Consider two cases.

Case 1. F _X ^m ∈ A ^′ .

Since (q _X ^(n,m) ) ⁻¹ (A ^′ ) is homeomorphic to A ^′ , it follows that dim[(q _X ^(n,m) ) ⁻¹ (A ^′ )] ≤ k − 2.

Case 2. F _X ^m ∈ A ^′ .

By Lemma 2.11 and Lemma 2.12, dim[X] = 1. Observe that (q _X ^(n,m) ) ⁻¹ (A ^′ ) = (q _X ^(n,m) ) ⁻¹ (A ^′ − {F _X ^m }) ∪ (q _X ^(n,m) ) ⁻¹ ({F _X ^m }) = (q _X ^(n,m) ) ⁻¹ (A ^′ − {F _X ^m }) ∪ F _m (X). By Lemma 2.13, dim[F _m (X)] ≤ m. Since m ≤ n ≤ k − 2 and dim[(q _X ^(n,m) ) ⁻¹ (A ^′ − {F _X ^m })] ≤ Lemma 2.13, dim[Fm(X)] ≤ m. Since m ≤ n ≤ k−2 and dim[(q ^(n,m) _X )−1(A′ −{F ^m _X })] ≤ dim[A′] ≤ k − 2, by Lemma 2.14, we conclude that dim[(q ^(n,m) _X )−1(A′)] ≤ k − 2.

The following result extends [¹⁷, Corollary 3.10].

Theorem 3.10. Let n,m ∈ ℕ be such that m ≤ n. The hyperspaces HS ⁿ _m ([0, 1]) and HS ⁿ _m (S ¹) are 2n−dimensional Cantor manifolds.

Proof. Case n = m is already proved in [¹⁷, Corollary 3.10].

Suppose that n > m. By Lemma 2.15 we have that C _n ([0, 1]) and C _n (S1) are 2n−dimensional Cantor manifolds. Since n ≥ 2 and 2n ≥ n + 2, the result follows from Theorem 3.9.

Question 3.11. For what continua X does the natural embedding in the proof of The-orem 3.3 embed HS _m ^s (X) as a retract of HS _m ⁿ (X)? In particular, what about the case when X is S ¹?

Question 3.12. For what continua X, can HS _m ^s (X) be embedded in HS _m ⁿ (X) as a retract (m ≤ s < n)?

According to [⁶, Theorem 4.4] which states that if X is a contractible continuum and n, m ∈ ℕ with m ≤ n, then HS _m ⁿ (X) is contractible, the following question arises:

Question 3.13. What continua X have the property that HS _m ⁿ (X) is contractible for each n, m ∈ ℕ with m ≤ n?

Question 3.14. [⁶, Question 7.5] If X is decomposable and n, m ∈ ℕ with m < n, is HS _m ⁿ (X) locally arcwise connected at F _X ^m ?

Question 3.15. What continua X have the property that HS _m ⁿ (X) is pseudo−contractible for each n, m ∈ ℕ with m ≤ n?