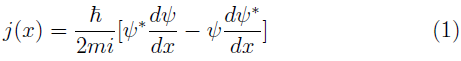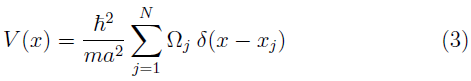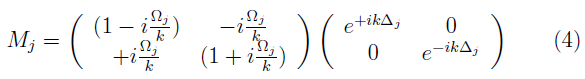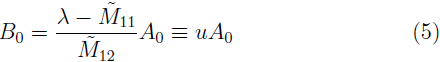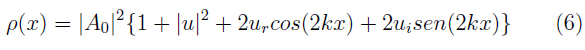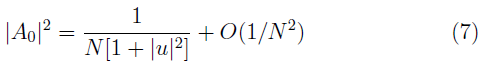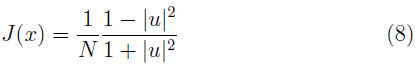Introducción
Aunque el avance de la tecnología actual ha hecho posible el desarrollo de técnicas que permiten manufacturar dispositivos de baja dimensionalidad [1] (e.g. epitaxia de haces moleculares) esta no esta libre de ciertos defectos e imperfecciones que van a afectar en cierta medida sus propiedades mecánicas, ópticas, electrónicas, magnéticas. Debido a esto, desarrollar estudios tanto teorico-computacionales como experimentales, orientados a evaluar los efectos de dichas imperfecciones (desorden), resultan relevantes en el planeamiento y diseño de tales dispositivos. Particularmente, la necesidad de contar con sistemas (cuasi)-unidimensionales (1D) (e.g. superredes, nanoalambres) con perspectivas en el desarrollo de transistores e interconectores, estimulan el desarrollo de estudios acerca de los efectos que estas imperfecciones puedan tener sobre sus propiedades ópticas y electrónicas. Tomando en cuenta ello, en el presente trabajo se aborda el estudio de los efectos del desorden estructural y químico sobre las propiedades de transporte electrónico en un modelo de solido 1D.
Uno de los trabajos pioneros en el estudio de los efectos del desorden fue desarrollado por P.W. Anderson [2], quien encontro que dependiendo de la dimensionalidad del sistema y el nivel del desorden, se puede producir la inhibición del transporte electrónico. Estudios realizados en nanopartículas [3] indican también que las propiedades de transporte se ven afectadas por el tipo de desorden. Con la finalidad de estudiar los efectos de los tipos de desorden indicados, se considera como sistema de referencia el modelo de Kronig-Penney [4] en su representación como una cadena de potenciales tipo delta. Sistemas del tipo Kronig-Penney han sido utilizados también para evaluar la resistencia eléctrica a partir de su relation con la densidad de estados [5]. En el presente trabajo, el desorden estructural es incluido en el modelo de Kronig-Penney permitiendo la variación aleatoria (distribución uniforme) en las posiciones de los potenciales, y el desorden químico, variando sus intensidades respectivas. La evaluación de los efectos del desorden sobre el estado electrónico, representado mediante una combinación de ondas planas, se realiza mediante el flujo electrónico y la medida estadística de complejidad propuesta por López-Ruiz, Mancini y Calbet (LMC) [6]. Esta medida de complejidad (C) ha sido utilizada para caracterizar propiedades conformacionales de sistemas de muchos cuerpos [7], [8]. La determinación de la función de onda electrónica, necesaria para el cálculo del flujo electrónico y la medida estadística de complejidad, se realiza mediante el método de la matriz de transferencia. Esta metodología, de aplicación general al transporte fotofónico y electrónico [9], [10], ha permitido profundizar en el estudio de sistemas unidimensionales desordenados [11].
El trabajo está organizado como sigue: en la sección 2 se presentan las cantidades utilizadas para comparar los efectos del desorden. Luego, en la sección 3, se presentan los modelos de Kronig-Penney con desorden estructural y químico, así como la metodología de la matriz de transferencia que se utiliza en la determinación del estado electrónico. En la sección 4 se realiza la discusión de los resultados obtenidos a partir del cálculo de la complejidad y el flujo electrónico para un estado electrónico representativo. Finalmente, las conclusiones se presentan en la sección 5.
1. Conceptos básicos
1.1. Flujo electrónico
Una cantidad representativa de una partícula cuántica es su función de onda Ψ(x). Esta se obtiene al resolver la ecuación de Schrödinger independiente del tiempo,
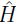 Ψ = E Ψ, que constituye un problema del valor propio. Además, en la mecánica cuántica se define el flujo electrónico, j (x), como:
Ψ = E Ψ, que constituye un problema del valor propio. Además, en la mecánica cuántica se define el flujo electrónico, j (x), como:
Para casos en que la densidad de probabilidad se mantiene constante (estados estacionarios) y para potenciales de interacción reales (V(x) Є ℝ), se cumple la conservación del flujo electrónico.
1.2. Complejidad y medida estadística LMC
La noción de complejidad ha venido desarrollándose desde mediados del siglo pasado y constituye una característica asociada al nivel de organización o jerarquía en un sistema [12] como resultado de una interacción no simple de sus componentes [13]. Algunos indicadores de complejidad, denominados medidas de complejidad, han sido propuestos en el área de la física, como por ejemplo: la medida efectiva de complejidad [14], la profundidad termodinámica [15], la medida estadística de complejidad LMC [6]. Justamente, esta última ha sido aplicada con éxito en la caracterización de regímenes de transición en sistemas dinámicos caóticos [6], [16], evolución dinámica de sistemas fuera del equilibrio [17], propiedades conformacionales de sistemas de muchos cuerpos [18], [8], estructura de bandas en sistemas cristalinos [19], entre otros. La medida estadística de complejidad LMC (C), propuesta por López-Ruiz, Mancini y Calbet [6], parte de la noción intuitiva que los sistemas idealizados completamente ordenado (cristal) y completamente desordenado (gas ideal) no tienen complejidad alguna (C = 0). Asimismo, consideran que el estado con un máximo de complejidad subyace en la región intermedida entre estos extremos. La cantidad estadística básica asociada al sistema bajo estudio es la probabilidad, p
i
, para un sistema con una distribución discreta de estados o la densidad de probabilidad, p(x), para un sistema con una distribución continua de estados. Lopez-Ruiz et al. [6] definieron C = HD para una distribución discreta de estados, donde H = -
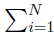 p
i
ln p
i
es la entropía de Shannon [20] y D =
p
i
ln p
i
es la entropía de Shannon [20] y D =
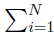 (p
i
- 1/N)2 es el desequilibrio, tal que
(p
i
- 1/N)2 es el desequilibrio, tal que 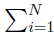 p
i
= 1. Posteriormente, Catalan et al. [21] reformularon la medida estadística de complejidad para una distribución continua de estados como:
p
i
= 1. Posteriormente, Catalan et al. [21] reformularon la medida estadística de complejidad para una distribución continua de estados como:
con H = - ∫
Λ
p(x) ln p(x)dx y D = ∫
Λ
p
2
(x)dx, tal que ∫
Λ
p(x) = 1. H se considera una medida del contenido de información del sistema y D constituye una medida de la localización electrónica. El calculo de H, D y C se realiza tomando en cuenta variables adimensionales
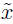 /a → x,
/a → x, 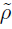 a → p) y con a = 1 Å (longitud de referencia). Catalán et al. [21] determinaron que el mínimo de complejidad (C = 1) se obtiene para la distribución equiprobable (densidad de probabilidad rectangular) y que el máximo de complejidad (con un valor no específico) se consigue para una distribución caracterizada con estados preferenciales.
a → p) y con a = 1 Å (longitud de referencia). Catalán et al. [21] determinaron que el mínimo de complejidad (C = 1) se obtiene para la distribución equiprobable (densidad de probabilidad rectangular) y que el máximo de complejidad (con un valor no específico) se consigue para una distribución caracterizada con estados preferenciales.
2. Modelo y metodología de cálculo
Un modelo paradigmático de la materia condensada es el modelo de Kronig-Penney (MKP) [4]. Aunque simple, este modelo de sólido cristalino 1D permite reproducir características relevantes de sistemas reales, como por ejemplo la distribución de las energías permitidas en bandas de energía, que constituye un ingrediente para distinguir a un material como metal, semiconductor o aislante [22]. Para el presente estudio, la interacción de un electrón con una cadena de átomos (sólido 1D), separados una distancia a, se representa mediante el siguiente potencial:
con Ω j y δ(x - xj) cantidades adimensionales. El desorden estructural en el MKP (Figura 1-(a)) se consigue al ubicar los potenciales de igual intensidad (Ω j = Ω, ∀j) en posiciones aleatorias alrededor de las posiciones originales (i.e. equidistantes del MKP), tal que x j = j + 0,25Єs, con Єs un numero aleatorio entre [-W, +W]. El parámetro W permite modular el nivel de desorden en la cadena, de modo que cuando W = 1 se considera un alejamiento de hasta 0,25 alrededor de la posición original del MKP (W = 0).
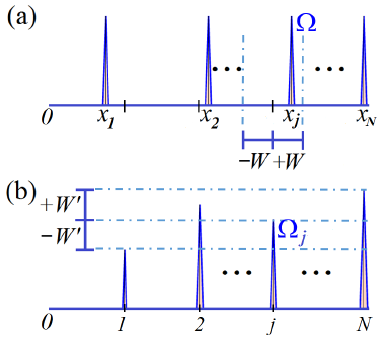
FIGURA 1 Representación esquemática del modelo propuesto de solido 1D con: (a) desorden estructural, y (b) desorden químico.
El desorden químico en el MKP (Figura 1-(b)) se produce al mantener los potenciales en sus posiciones equidistantes (xj = j, ∀j) pero permitiendo que las intensidades de los potenciales varíen de forma aleatoria: es decir, Ω j = Ω + ЄcΩ, con Єc un numero aleatorio entre [-W', +W']. Cuando el parametro de desorden W' = 1, la intensidad de los potenciales varía tal que 0 < Ω j < 2Ω.
Con la finalidad de evaluar los efectos del desorden, se calcula el flujo electrónico (j (x)) y la medida estadística de complejidad LMC (C), a partir de la función de onda electrónica. Esta se obtiene mediante el método de la matriz de transferencia que constituye una metodología de amplia aplicación en el estudio de la propagación de partículas cuánticas en medios estratificados [10],[23]. A continuación se describe brevemente como se ha procedido en el presente trabajo.
Considere un potencial delta de intensidad Ωj ubicado en la posición x
j
tal que las ondas planas en las regiones adyacentes, para un vector de estado adimensional (
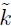 a → k), se expresan como: Ψ
j(x) = Aje
+ikx
+ B
je
-
ikx
en (xj,xj+1) y Ψ
j
-1(x) = A
j-1
e+
ikx
+ B
j-1
e
-ikx
en (xj-1,xj-). El método de la matriz de transferencia permite relacionar las amplitudes de las ondas alrededor de la posicióon x
j
mediante una matriz de transferencia local M
j
que viene dada por:
a → k), se expresan como: Ψ
j(x) = Aje
+ikx
+ B
je
-
ikx
en (xj,xj+1) y Ψ
j
-1(x) = A
j-1
e+
ikx
+ B
j-1
e
-ikx
en (xj-1,xj-). El método de la matriz de transferencia permite relacionar las amplitudes de las ondas alrededor de la posicióon x
j
mediante una matriz de transferencia local M
j
que viene dada por:
con Δj ≡ xj - xj-1. En la matriz de transferencia local (ecuación (4)), el primer factor considera la variabilidad en la intensidad del potencial (desorden químico) y el segundo la variación en las distancias entre potenciales (desorden estructural). Las múltiples dispersiones que experimenta la onda electrónica a lo largo de la cadena de potenciales (N = L/α) son consideradas mediante la matriz de transferencia global, M = M
N
M
N-1
... M
2
M
1
, y cumple las siguientes propiedades:
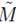 11 =
11 =
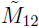 , =
, =
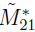 y det(
y det(
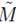 ) = 1. Tomando en cuenta la simetriza s de la matriz de transferencia global (s ≡ ½ (
) = 1. Tomando en cuenta la simetriza s de la matriz de transferencia global (s ≡ ½ (
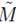 11 +
11 +
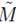 22)) y considerando el planteamiento del problema del valor propio y la conservación del flujo electrónico se obtiene que s2 ≤ 1. Está relación impone una restricción sobre los posibles valores de k y por consiguiente sobre las energías (equivalente a la condición que origina la distribución de energías en bandas permitidas y prohibidas). Asimismo, se obtiene una relación entre las amplitudes incidente (A0) y reflejada (B0) cuyo cociente se caracteriza mediante u:
22)) y considerando el planteamiento del problema del valor propio y la conservación del flujo electrónico se obtiene que s2 ≤ 1. Está relación impone una restricción sobre los posibles valores de k y por consiguiente sobre las energías (equivalente a la condición que origina la distribución de energías en bandas permitidas y prohibidas). Asimismo, se obtiene una relación entre las amplitudes incidente (A0) y reflejada (B0) cuyo cociente se caracteriza mediante u:
Justamente u contiene toda la information de los detalles del tipo de desorden evaluado pues es función de la matriz de transferencia global (ecuación (5)). Se verifica también, a partir de la conservación del flujo electrónico, que |u|2 = |Bj|2/|A j |2, ∀j. Si además, se toma en cuenta la condición de normalización a lo largo de la cadena, se puede determinar la función de onda electrónica (salvo un factor de fase) y, por consiguiente, la densidad de probabilidad, p(x) = |Ψ(x)|2. Así, tenemos que,
con u r y u i parte real e imaginaria del cociente de amplitudes u. Además,
que resulta de considerar cadenas de longitud larga (N > 200). Al definir el flujo electrónico normalizado como J(x) = j(x)/(
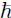 k/m) se deduce que J(x) = |A0|2[1 -|u|2]. Si se considera además la ecuación (7), el flujo electrónico normalizado se puede expresar como:
k/m) se deduce que J(x) = |A0|2[1 -|u|2]. Si se considera además la ecuación (7), el flujo electrónico normalizado se puede expresar como:
De las ecuaciones (6) - (8) se observa que tanto la función de densidad de probabilidad, p(x), como el flujo electrónico normalizado, J(x), dependen de |u|. Por ello, |u| constituye una cantidad relevante en la evolución de los efectos del desorden, como se mostrará en la siguiente sección.
3. Resultados y discusión
Los cálculos mostrados a continuación se han realizado para el estado electrónico k = 8,36 (en unidades adimensionales, definidas en la sección previa) correspondiente al centro de la tercera banda del MKP y con Ω = 4. Así, conocida la densidad de probabilidad p(x) (ecuación (6)) se obtienen la complejidad C (a partir de H y D) y el flujo electrónico normalizado J (ecuaciones (2) y (8)). Con la finalidad que los resultados sean representativos del tipo de desorden analizado y no de una configuración específica, se evalúan valores promedio 〈H〉, 〈D〉, 〈C〉 y 〈J〉, que se obtienen a partir de un conjunto de 400 muestras para el desorden químico y 200 muestras para el desorden estructural. Los tamaños de las muestras están restringidas por limitaciones computacionales.
La inclusión de desorden tanto estructural (Figura 2-(a)) como químico (Figura 2-(b)) en el MKP, produce la reducción de la entropía y el crecimiento del desequilibrio. La entropía disminuye asintóticamente hacia un valor que muestra su dependencia con la longitud de la cadena. De manera opuesta, el desequilibrio aumenta hasta un valor de saturación que también depende de la longitud de la cadena. Cabe mencionar que el comportamiento complementario evidenciado para la entropía y el desequilibrio, a medida que se incrementa el desorden tanto estructural como químico, tiene correspondencia con lo esperado según la formulación inicial de la medida estadística de complejidad C propuesta por Lopez-Ruiz et al. [6].
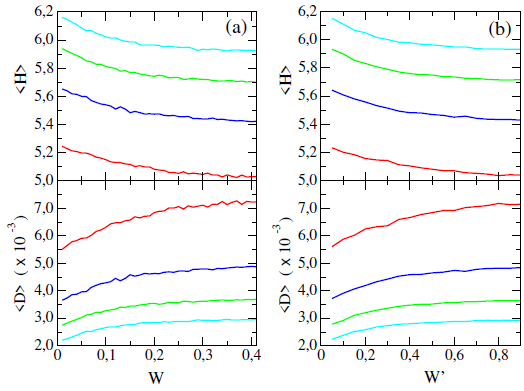
FIGURA 2 Valores promedio de la entropía y el desequilibrio para cadenas de N = 200 (rojo), 300 (azul), 400 (verde) y 500 (cian) con (a) desorden estructural y (b) desorden químico, para el vector de estado k = 8, 36 (centro de la tercera banda del MKP).
El sistema en estudio puede considerarse compuesto por el subsistema de los electrones y el subsistema de la cadena de potenciales. Puesto que el sistema completo constituye un sistema aislado, la reducción de la entropía en el subsistema de los electrones se efectuó conforme el desorden en el subsistema de la cadena de potenciales aumenta. El incremento de la entropía del sistema completo requerido por la segunda ley de la termodinámica no limita la posibilidad del ordenamiento [24] en el subsistema de los electrones. Más aún, el crecimiento del desequilibrio (también conocido como razón de participación inversa-IPR), corrobora el resultado ya observado mediante la entropía e indica un ordenamiento en el subsistema de los electrones a medida que el desorden en el sistema completo se incrementa.
El mencionado ordenamiento surge en el módulo de u (cociente de las amplitudes de las ondas reflejada e incidente) tal como se evidencia en la Figura 3. Asimismo, se observa que a partir de un tópico nivel de desorden en el subsistema de electrones, tanto para el caso del desorden estructural (Figura 3-(a)) como químico (Figura 3-(b)), se obtiene un valor preferencial en Más aún, el valor preferencial, para ambos tipos de desorden, corresponde a |u| = 1, lo que indica la igualdad de las amplitudes de las ondas reflejada e incidente. Es justamente el ordenamiento en las amplitudes lo que genera la reducción de la entropía y el incremento del desequilibrio.
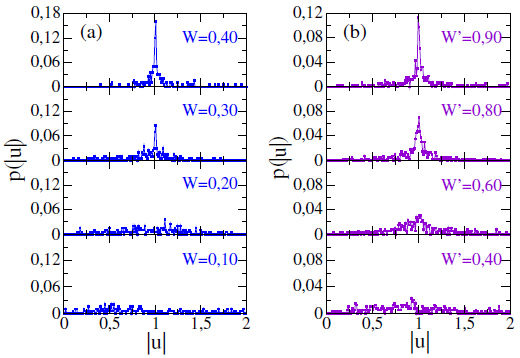
FIGURA 3 Probabilidad en función del módulo del cociente de amplitudes para el modelo de Kronig-Penney considerando tanto (a) desorden estructural como (b) desorden químico. Los cálculos han sido realizados para el vector de estado k = 8, 36 (centro de la tercera banda del MKP).
Los efectos de la inclusión del desorden estructural en el MKP, evaluados a partir del comportamiento de la medida estadística de complejidad (Figura 4-(a)) y del flujo de probabilidad (Figura 4-(b)) para diferentes niveles de desorden, indican una correspondencia entre el máximo de complejidad (〈C〉 ≈ 1,104) y el mínimo del flujo electrónico (〈J〉 ≈ 0). Justamente, ambos extremos se alcanzan a partir de un nivel de desorden característico de W ≈ 0, 30, con una leve dependencia de la longitud de la cadena de potenciales. Este nivel de desorden, para el cual el flujo electrónico prácticamente es despreciable, corresponde a una variación de 0,09 alrededor de las posiciones ideales de los potenciales del MKP (sin desorden). Las variaciones observadas en los comportamientos de 〈C〉 y 〈J〉 son consecuencia del tamaño de la muestra.
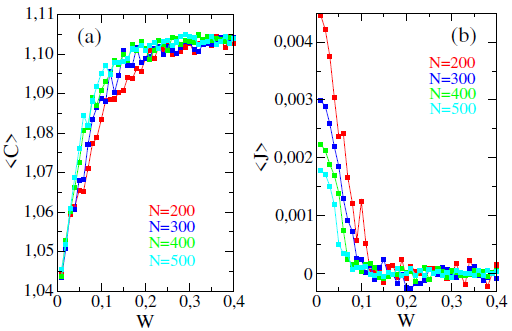
FIGURA 4 (a) Complejidad y (b) flujo electrónico promedios en función del nivel de desorden estructural (W) para el vector de estado k = 8, 36 (centro de la tercera banda del MKP).
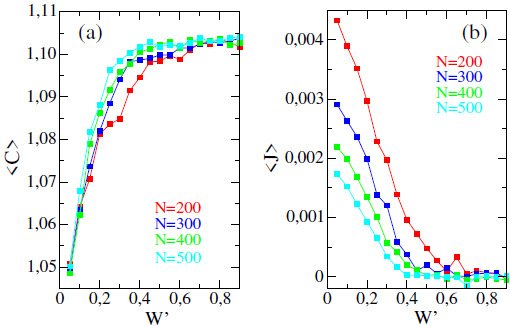
FIGURA 5 (a) Complejidad y (b) flujo electrónico promedios en función del nivel de desorden químico (W') para el vector de estado k = 8, 36 (centro de la tercera banda del MKP).
La inclusión de desorden químico en el MKP produce el crecimiento de la complejidad del estado electrónico a medida que se incrementa el nivel de desorden hasta un valor de saturación asintótico (Figura 5-(a)) correspondiente a 〈C〉 ≈ 1,104. Paralelamente, en la Figura 5-(b) se observa la reducción del flujo de probabilidad a medida que el desorden químico se incrementa, indicando la inhibición del transporte electrónico en el sistema para un nivel de desorden de W' ≈ 0, 70, lo que equivale a una variación en la intensidad de los potenciales tal que 0, 45Ω < Ωj < 1, 55Ω. Aunque tanto 〈C〉 como 〈J〉 muestran una leve dependencia de la longitud de la cadena de potenciales, el nivel de desorden para el cual el flujo electrónico se vuelve despreciable (〈J〉 ≈ 0) caracteriza también el valor umbral de desorden donde se alcanza el máximo de complejidad.
El crecimiento de la complejidad hacia un valor de saturación (Figuras 4-(a) y 5-(a)) también ha sido reportado en el caso del modelo del potencial delta de Dirac gemelo (modelo de dos potenciales delta de Dirac) como consecuencia del incremento de la separación entre los potenciales [25].
Conclusiones
La inclusion de desorden, tanto estructural como químico, produce el incremento en la complejidad LMC de un estado electrónico representativo de un sistema metálico (k = 8,36, centro de la tercera banda en el MKP) hacia un valor asintótico. A su vez, el incremento de desorden produce una reducción del flujo electrónico hasta llegar a valores despreciables, lo cual indica la inhibición del transporte electrónico. Los resultados de máxima complejidad y mínimo flujo electrónico se alcanzan para un nivel de desorden característico que depende del tipo de desorden incluido en el sistema a consecuencia de la igualdad de las amplitudes electrónicas incidente y reflejada. El comportamiento complementario encontrado entre C y J, tanto en el caso del desorden estructural como químico, permite considerar a la medida estadística de complejidad LMC como un indicador relevante de las propiedades de transporte electrónico.